风电机组混合型塔筒静强度分析与模态分析*

卢华兴，陈明阳，刘 伟，孙传宗，陈 雷

(1. 国家电投集团科学技术研究院有限公司，北京 102209； 2. 沈阳工业大学 机械工程学院，沈阳 110870)

随着风力发电技术的不断成熟以及风电机组单机容量的不断增加，风电机组塔筒的结构成为一个热门话题[1-2].风电机组塔筒质量占风电机组总质量的一半，是风电机组重要的承载部件，因此，塔筒的设计在风电机组的设计中十分重要[3-5].

目前，针对风电机组塔筒已有一些相关研究.河海大学的张羽等[6-7]总结了塔架的设计理论体系，指出现阶段风电机组的塔架设计仍然以锥形塔筒为主，并预测混合型塔架结构形式会逐渐投入使用；The Concrete Centre[8]分别设计了2和4.5 MW两种预应力混凝土风电塔架结构，塔高分别为70和100 m，塔架的基础为钢筋混凝土，研究表明，与钢塔架相比较，相同级别的混凝土塔架造价低30%，使用寿命提升至40～60年；刘贻雄[9]分析了现代风电机组中典型的塔筒结构，运用理论分析和数值模拟方法研究了塔筒的动力学特性、疲劳、屈曲稳定性，并得出在风电机组塔筒的结构动力响应中，低阶模态占主要地位，高阶模态对响应的贡献很小，阶数越高，其贡献就越小；李斌等[10]分析了大型风电机组普遍采用的锥台型塔筒，以优化锥台型塔筒结构设计为目标，利用SAP2000有限元分析软件对初选塔筒进行了静强度和刚度分析，根据优化分析结果，提出了一种下部为直筒型，上部为锥台型的新型塔筒形式.

本文首先对风电机组塔筒的载荷进行理论分析，并利用ANSYS软件建立有限元模型，进而分析所提出的混合型塔筒和其他两种结构塔筒的静强度性能和模态特性方面的差异，通过分析仿真结果得出，混合型塔筒性能相比传统型塔筒和加筋型塔筒有所提高，为风电机组塔筒结构的设计与选择提供参考.

1 风电机组塔筒结构模型

1.1 传统型与加筋型塔筒结构

风电机组目前应用最广泛的是由平板卷压焊接成型的圆筒型塔筒，其结构如图1所示，本文仿真模型参数如表1所示.

图1 传统型塔筒结构Fig.1 Structure of traditional tower

表1 传统型塔筒结构参数Tab.1 Structural parameters for traditional tower mm

加筋型塔筒在传统型塔筒的基础上采用加筋结构卷压焊接成型，其结构如图2所示.本文仿真模型参数如表2所示.与传统型塔筒相比，加筋结构使得塔筒的壁厚得以降低.

图2 加筋型塔筒结构Fig.2 Reinforced tower structure

表2 加筋型塔筒结构参数Tab.2 Structural parameters for reinforced tower mm

1.2 加筋与桁架混合的新型塔筒结构

本文提出一种加筋与桁架混合的新型塔筒，采用加筋结构并引入桁架，其结构如图3所示，本文仿真模型参数如表3所示，其中，筋板角度为2°.此种结构可以在降低塔筒壁厚的同时，通过加装桁架改善塔的静强度性能，并提高低阶模态频率.

图3 混合型塔筒结构Fig.3 Structure of hybrid tower

表3 混合型塔筒结构参数Tab.3 Structural parameters for hybrid tower mm

1.3 风电机组塔筒载荷分析

1.3.1 叶片载荷

叶片载荷来自叶片重力弯矩随叶片桨距角的变化而变化，叶片重力弯矩计算公式为

(1)

式中：mi为叶片每个微元的质量；r为每个微元的长度；R为叶片长度.

作用在叶片上的升力FL和阻力Fd分别为

(2)

(3)

式中：V为气流相对于叶素的速度；α为叶片攻角；c为叶片弦长；CL为升力系数；Cd为阻力系数；ρ为空气密度.由气动力引起的弯矩为

(4)

(5)

1.3.2 风轮载荷

风轮传递能量的同时也将载荷传递到其他部件，风轮载荷取决于风电机组运行的风况条件.风轮的轴向推力主要是风荷载对叶片的水平作用力，也是塔架顶部最大的水平荷载，其计算公式为

(6)

式中：CT为推力系数；A为风面积；Vp为额定风况下的风速.

当风电机组风能利用系数Cp取最大值时，CT取为8/9，其计算公式为

CT=4a(1-a)

(7)

Cp=4a(1-a)2

(8)

式中，a为轴流诱导因子，可由动量理论推导得出，即

(9)

当风向发生改变时，风电塔架会受到来自叶轮的偏转力，即

Fx=Fysinδcosδ

(10)

式中：δ为叶片轴线与风向的夹角；Fx为偏转力；Fy为气动载荷切向力.

当风轮旋转时，产生的风轮转矩和偏转力矩为

My=9 950Pη/ω

(11)

(12)

式中：P为发电机的功率；η为发电机效率；e为风轮扫略平面中心与塔筒中心垂直轴线的距离；ω为风轮转速.

因为距地面不同高度的风速不同，上下叶片受力不一样，所以会产生俯仰力矩Mx，其计算公式为

(13)

式中：V1为作用于风轮中心上三分之二叶片长度处的风速；V2为作用于风轮中心下三分之二叶片长度处的风速.

塔筒顶部的风轮和机舱等结构在遇到对流风时会产生旋转，从而产生陀螺力Fs1以及陀螺力矩Ms1，其表达式为

Fs1=eω2m

(14)

Ms1=ΩωI

(15)

式中：Ω为风机绕塔筒轴线的旋转角速度；I为风轮的旋转角速度；m为风轮和机舱的总质量.

1.3.3 塔架载荷

根据《高耸结构设计规范》(GB50315-2006)[11]规定，垂直作用于高耸结构表面单位面积上的风荷载标准值计算公式为

一个或多个相似时间序列组成一个时间序列类，时间序列类的相似性采用平均欧氏距离表征，平均欧氏距离越小，相似性越大，反之亦然。设有两个时间序列类X={Xi}m和Y={Yi}n，其中Xi和Yi为时间序列，则X和Y的平均欧氏距离DX,Y为

wk=βzμsμzw0

(16)

式中：wk为高耸结构z高度处的单位风荷载；w0为基本风压；μz为z高度处的风压高度变化系数；μs为风荷载体型系数；βz为z高度处的风振系数.

μz和βz的计算公式为

μz=(0.1z)0.32

(17)

βz=1+ξυθυθBφz/μz

(18)

式中：ξ为脉动增大系数，ξ=2.16；θυ为脉动影响系数；υ为结构在迎风面顶端宽度Dt与底端宽度Df的比值修正系数；θB为结构在迎风面z高度处的宽度Dz与底部宽度Df的比值；φz为第一振型系数，φz=(6z2H2-4z3H+z4)/(3H4)，其中，H为总高度，z为计算位置离地面的高度.

式(16)中w0可按如下公式计算：

(19)

风电机组塔筒塔身面荷载为

(20)

2 塔筒有限元建模

2.1 偏航坐标系

偏航坐标系以塔筒顶部连接机舱的基础面建立，原点位于塔筒顶部的中心点，如图4所示.

图4 偏航坐标系Fig.4 Yaw coordinate system

2.2 有限元建模

为了保证仿真结果的精确性和时效性，对塔筒进行有限元建模时做如下假设：

1) 塔筒截面为理想圆形，不计入加工误差或初始表面缺陷；

2) 承受外载荷作用的塔筒始终处于小变形、线弹性范围内；

3) 法兰之间的接触状态良好，不计入螺栓连接引起的边界非线性影响；

4) 考虑与传统型塔筒做横向比较，本文取同等截面处的传统型壁厚h为4 mm作为加筋型塔筒最小壁厚，从而统计得到相同高度处，加筋型塔筒截面积与传统型塔筒截面积之比大于等于98%.

图5～7分别为传统型、加筋型、混合型塔筒有限元模型.基于上述假设条件建立的三种塔筒的单元类型如表4所示，材料属性如表5所示.其中，传统型塔筒有限元模型总计55 650个单元，381 451个节点；加筋型塔筒总计138 330个单元，793 216个节点；加筋与桁架混合型塔筒总计141 770个单元，809 023个节点.

在偏航坐标系原点建立节点，并将其与相应塔顶法兰端面MPC刚性连接.在此中心节点施加6组极限载荷，形成载荷外边界，载荷数值如表6所示.约束塔筒底端面节点的全部自由度，形成位移约束边界.在此中心节点施加疲劳载荷单位值(Fx，y，z=10 000 N，Mx，y，z=100 000 N·m).

图5 传统型塔筒有限元模型Fig.5 Finite element model of traditional tower

图6 加筋型塔筒有限元模型Fig.6 Finite element model of reinforced tower

图7 混合型塔筒有限元模型Fig.7 Finite element model of hybrid tower

表4 三类塔筒采用的单元模型Tab.4 Unit models employed in three towers

表5 塔筒及桁架材料属性Tab.5 Material properties of tower and truss

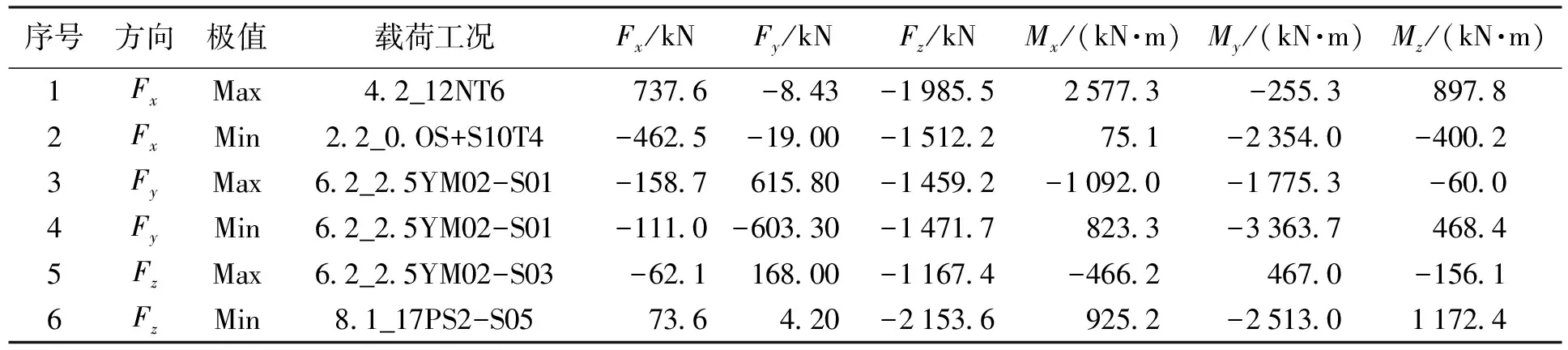
表6 机组塔筒塔顶处极端载荷Tab.6 Extreme loads at top part of wind turbine tower

3 仿真及结果分析

3.1 静强度分析

不同工况下塔筒的等效应力如图8～11所示.参照上述结构模型中的分段，不同工况下不同塔筒每段等效应力及位移对比值见表7.

分析表7可知，在同等载荷条件下，加筋型塔筒的最大位移大于传统型塔筒，两者比值多数在100.6%的临近区间，其中第2工况的最大位移比值最小，约为100.58%，第3工况的最大位移比值最大，约为100.66%；加筋与桁架混合型塔筒的最大位移均同样小于传统型塔筒，两者比值多数在66%临近区间，其中，第4工况的最大位移比值最小，约为58.03%，第1工况的最大位移比值最大，约为66.98%.由此可以推出，相比传统型塔筒，加筋型塔筒没有显著改变塔筒静刚度；加筋与桁架混合型塔筒静刚度增大约51%，刚度提高显著.

图8 工况1三种塔筒应力云图Fig.8 Stress nephograms of three towers under working condition 1

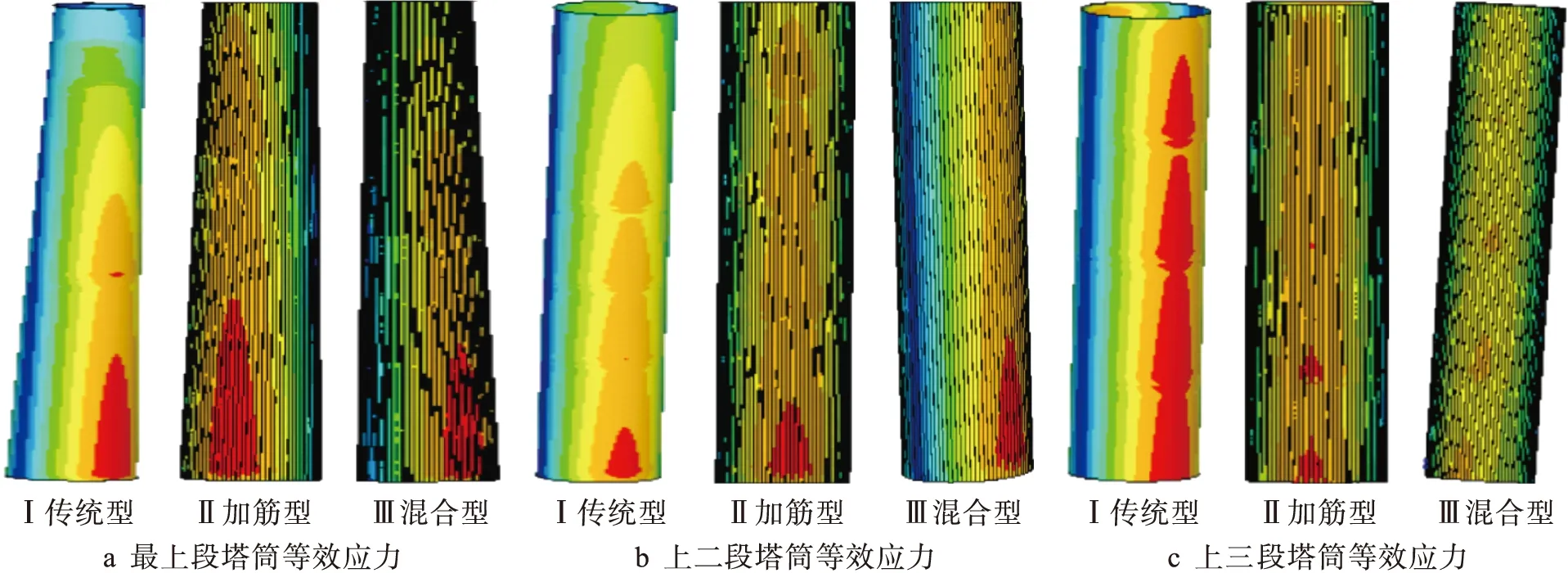
图9 工况2三种塔筒应力云图Fig.9 Stress nephograms of three towers under working condition 2

图10 工况3三种塔筒应力云图Fig.10 Stress nephograms of three towers under working condition 3

图11 工况4三种塔筒应力云图Fig.11 Stress nephograms of three towers under working condition 4

表7 三种塔筒等效应力、位移数值对比Tab.7 Comparison of equivalent stress and displacement value for three towers

3.2 模态分析

由有限元计算得到三种模型的模态振型如图12～14所示，模态频率如表8所示.三种模型的前6阶模态振型分别代表1阶横向整体振型、1阶纵向整体振型、2阶横向整体振型、2阶纵向整体振型、3阶横向整体振型、3阶纵向整体振型；传统型塔筒的第7～10阶振型分别代表1阶扭转振型、4阶横向整体振型、4阶纵向整体振型、2阶扭转振型；加筋型塔筒及加筋与桁架混合型塔筒的第7～10阶振型为塔筒局部模态振型.

图12 传统型塔筒前10阶模态振型Fig.12 First 10th modal shapes of traditional tower

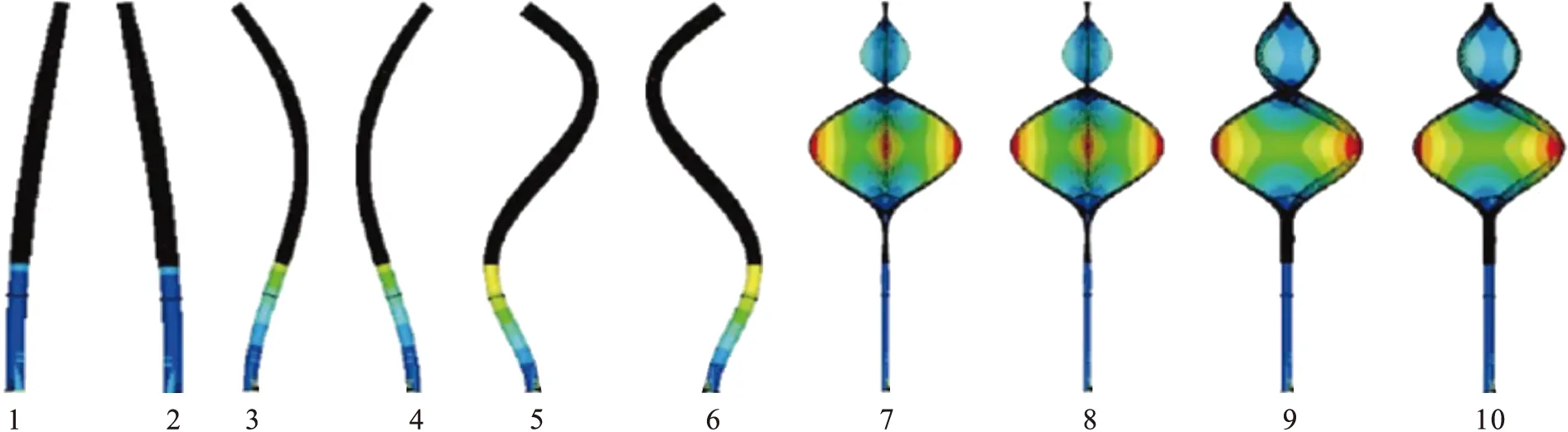
图13 加筋型塔筒前10阶模态振型Fig.13 First 10th modal shapes of reinforced tower

图14 混合型塔筒前10阶模态振型Fig.14 First 10th modal shapes of hybrid tower

判断风电机组系统是否稳定，就是判断塔架的固有频率是否与外界激励的频率耦合而发生振动.系统的低阶固有频率避开风轮旋转频率的1倍频率和3倍频率，对塔架固有频率进行计算可以分析固有频率是否会与风轮旋转频率重合，或者是否在一定的范围内避开了风轮旋转激励频率.塔架的固有频率必须在一定范围内避开这个值，工程上一般要求在±10%左右.

由表8可见，加筋型塔筒的前3阶整体模态频率值均小于同阶次的传统型塔筒频率值，其中，第1阶整体模态频率减少约0.32%，第2阶整体模态频率减少约1.81%，第3阶整体模态频率减少约3.38%.3阶以后的模态振型受局部结构影响较大，导致加筋型塔筒的模态频率比传统型塔筒的模态频率偏低.加筋与桁架混合型塔筒的前2阶整体模态频率值均大于同阶次的传统型塔筒频率值，其中，第1阶整体模态频率超出约25.8%，第2阶整体模态频率超出约17.8%.3阶以后由于模态振型受局部结构的影响较大，使得在比较最下端塔筒占主要形变的第3阶整体模态频率时，加筋与桁架混合型塔筒的模态频率均比传统型塔筒模态频率低.

表8 三种模型的固有频率Tab.8 Inherent frequencies of three models Hz

风电机组工作时，叶轮运行会对塔筒系统产生激励.为了确保风电机组的安全运行，必须通过计算分析配制好叶轮叶片和塔筒系统的固有振动特性，避开叶轮转动时产生的激励频率，避免共振现象的发生.

图15为塔筒Campbell图.由图15可知，本文中传统型塔筒在转速ω∈[0，10.11] r/min区间为刚性塔筒，ω∈[12.36，30.34] r/min区间为柔性塔筒；加筋型塔筒在转速ω∈[0，10.08] r/min区间为刚性塔筒，ω∈[12.31，30.24] r/min区间为柔性塔筒；加筋与桁架混合型塔筒在转速ω∈[0，120.73] r/min区间为刚性塔筒，在ω∈[15.55，38.19] r/min区间为柔性塔筒.就本文而言，加筋型结构没有显著改变塔筒模态频率；而加筋与桁架混合型结构使得塔筒刚性设计转速区间提高了1.6 r/min，这有利于刚性塔筒的结构设计.

图15 塔筒Campbell图Fig.15 Campbell diagram of tower

4 结 论

本文基于ANSYS软件针对三种结构的塔筒进行静强度分析和模态分析，得到如下结论：在保证壁厚相同的约束下，加筋型和混合型塔筒的等效应力极值较传统型有所增加，同时混合型塔筒的刚度较传统型有显著提高，提高幅度达到了51%.可见所提出的加筋型与桁架混合型塔筒结构有利于提高刚度，抑制变形.模态方面，加筋型与桁架混合型塔筒能够显著提高低阶整体模态频率.其中，第1阶整体模态频率提高25.8%，第2阶整体模态频率提高17.8%.同时，就本文风电机组而言，加筋型与桁架混合型结构使得塔筒刚性设计转速区间提高了1.6 r/min.因此，加筋型与桁架混合型结构设计有利于刚性塔筒设计.

基于以上分析可以得出，加筋与桁架混合的新型塔筒结构在静强度方面优于传统型塔筒和加筋型塔筒.混合型塔筒的低阶模态频率高于其他两种结构塔筒，同时刚性设计转速区间有所提高.就本文而言，混合型塔筒更加有利于塔筒刚性设计.