基于损伤力学的裂缝性储层流固耦合数值模拟*

蔡 鑫，刘 威，沈新普，张 璋

(中国石油大学 石油工程学院，山东 青岛 266580)

裂缝性储层的渗透能力主要取决于裂缝的连通性和导流能力.相较于常规储层，裂缝性储层表现出更强的应力敏感性.因此，需要在进行储层数值模拟的同时考虑地质力学因素对裂缝的影响.

由于裂缝的存在，裂缝性储层岩石的性质十分复杂[1].常规油藏数值模拟中，通常采用双重孔隙模型来计算裂缝性储层中流体的流动.模型中储层可以分为两个部分，基质系统和裂缝系统.基质系统渗透率低，但是孔隙度高，主要起储集作用；裂缝系统渗透率高，但孔隙度低，几乎没有储集效果，只提供渗流通道.许多学者基于Biot孔隙介质弹性理论，利用双重孔隙介质模型进行流固耦合计算.例如，房平亮等[2]建立了基质和裂缝变形的流固耦合数学模型；Wang等[3]采用离散裂缝模型和双重介质模型相结合的方法研究了压裂后的缝网变化；Luo等[4]建立了平行裂缝岩石的本构方程，以基质孔隙度为耦合参数进行了裂缝性油藏数值模拟；Wang[5]推导了全耦合的双重孔隙介质模型，并利用有限元方法进行了求解.

目前，油藏数值模拟中通常采用离散化裂缝模型(DFM)处理裂缝，DFM具有网格精细的特点，适用于模拟复杂的多组分流体[6].由于DFM需要大量的网格加密，影响建模和模拟的速度，很难应用于裂缝发育的油田研究.在连续损伤力学中，采用损伤变量来描述裂缝对材料的影响[7].由于连续损伤力学将裂缝网络分布转化为损伤场分布，计算效率得到保障，同时可以考虑裂缝扩展过程，因此，适用于裂缝发育和复杂应力区块[8].目前，连续损伤力学理论已经逐渐被应用于石油工程行业，用于计算地层岩石中裂缝的萌生和扩展[9].

本文采用塑性损伤有限元方法计算裂缝变形，结合双重孔隙介质模型，建立适用于裂缝性储层的流固耦合油藏数值模拟方法.采用迭代耦合方法进行数值求解，以裂缝渗透率为耦合参数，建立损伤变量与裂缝渗透率的数学表达式，模拟裂缝性储层注采过程，研究裂缝变形对裂缝性储层生产动态的影响，为油田高效开采提供理论支撑.

1 塑性损伤本构模型

本文采用塑性连续损伤模型[10]，该模型适用于准脆性材料，例如岩石和混凝土材料在单调、循环或动载荷作用下的力学行为分析.

1.1 单轴受力行为

损伤的出现和演化会导致材料刚度退化，单轴拉压作用下的应力应变关系可分别表示为

(1)

(2)

塑性损伤模型的损伤演化机理分为两个部分：拉力作用下的开裂和压力作用下的压溃.塑性加载的演化由两个独立的硬化变量描述：拉力加载引起的等效塑性拉应变和压力加载引起的等效塑性压应变.对于单轴拉伸行为，如图1所示，在拉应力达到峰值之前材料表现出线弹性.当拉应力超过峰值后，材料中产生微裂缝，损伤出现，材料出现“软化”现象，最终导致应变集中.对于单轴压缩行为，如图2所示，与拉伸行为不同的是，在压应力达到峰值前为应变硬化阶段，超过峰值后为应变软化阶段，材料中出现应变集中.

图1 单轴受拉示意图Fig.1 Schematic uniaxial tension

图2 单轴受压示意图Fig.2 Schematic uniaxial compression

1.2 单轴循环载荷

材料在循环载荷作用下(如地层岩石在生产或注水过程中)，微裂缝的张开和闭合会导致材料具有明显的非线性行为.材料损伤后的弹性模量E与完整无损材料弹性模量E0的关系为

E=(1-D)E0

(3)

式中，D为综合损伤因子，为拉伸损伤dt和压缩损伤dc的函数，其表达式为

1-D=(1-stdt)(1-scdc)

(4)

其中，st和sc为应力状态函数，其表达式为

st=1-wtr*(σ) (0≤wt≤1)

(5)

sc=1-wc(1-r*(σ)) (0≤wc≤1)

(6)

(7)

其中，wt和wc为刚度恢复因子.

1.3 流动法则

模型采用非关联的塑性流动法则，塑性势函数取为Drucker-Prager双曲函数形式，即

(8)

式中：ψ为膨胀角；σm为单轴抗拉强度；ξ为势函数偏心率，用于描述势函数向其渐近线逼近的速度，一般取值为0.1；ps为有效静水压力；a为Mises等效应力.

1.4 损伤与裂缝

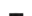
(9)

(10)

式中：u为裂缝开度；λ为损伤区域宽度因子；lc为材料特征长度；Bt为材料参数；Kf为裂缝渗透率.

2 双重孔隙介质流体流动方程

本文给出双重孔隙介质油水两项流动方程，基本假设如下：1)裂缝系统和基质系统皆由油相和水相饱和，两个系统互相重叠且有各自的连续性方程；2)油相和水相在裂缝和基质系统中的流动遵循达西定律；3)裂缝系统与基质系统之间窜流交换受压力差控制.

由于本文重点关注裂缝变化对流体流动的影响，因此，忽略固体相运移对达西定律的影响.裂缝系统和基质系统的连续性方程为

(11)

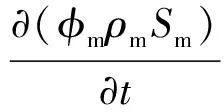
(12)

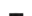
Sw+So=1

(13)

式中：Sw为水相饱和度；So为油相饱和度.

3 双重孔隙模型有效应力方程

对于双重孔隙介质模型，存在基质孔隙压力和裂缝孔隙压力，引入Biot耦合系数，有效应力方程为

(14)

式中：σe为地层有效应力；βm和βf分别为基质和裂缝系统的有效压力系数；δ为克罗内克函数.

对于岩石材料，裂缝可以看做一个较大的孔隙，基质孔隙压力和裂缝孔隙压力对地层变形有相同的影响，因此，式(14)可近似为

(15)

4 流固耦合数值模拟结果和分析

为了研究裂缝变形对油藏生产的影响，本文以Kazemi经典双重孔隙油藏模型数据为例，对一注一采裂缝性储层开发过程中的储层压力、裂缝物性等变化规律进行了数值模拟.模型主要参数为：地层尺寸为182 m×182 m×9.14 m，地层顶深3 000 m，初始孔隙压力为29.4 MPa，地层垂向应力为46.7 MPa，地层水平最大最小主应力均为32.7 MPa.储层裂缝渗透率从10 μm2改为0.2 μm2，裂缝渗透率从1%改为0.14%.地层中包含三组裂缝，具体数据如表1所示.储层边角处有一口注入井，注水量为30 m3/d，同时在注入井对角处有一口生产井，产液量为32 m3/d.

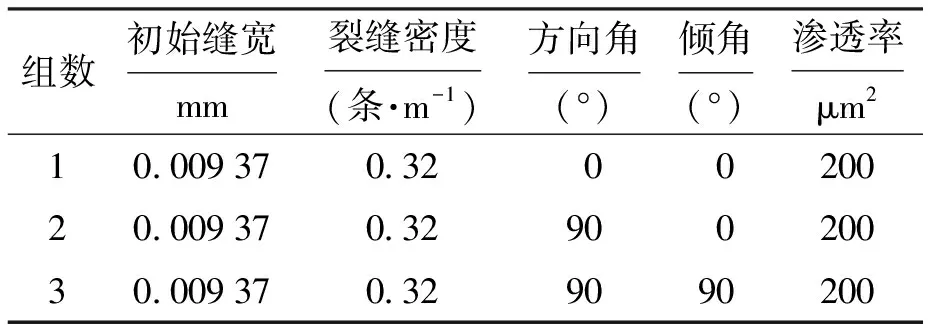
表1 地层裂缝参数Tab.1 Fracture parameters for stratum

裂缝性储层的初始损伤为0.1，储层岩石弹性模量为26 GPa，泊松比为0.16，特征长度为0.02 m，λ为2，Bt为900.根据式(10)得到损伤与地层裂缝渗透率关系曲线，如图3所示.可以看出当损伤因子小于0.05时，岩石中只存在弥散的微裂缝，裂缝渗透率变化较小.当损伤因子超过0.05时，微裂缝逐渐聚集成宏观裂缝，裂缝渗透率急剧增加.

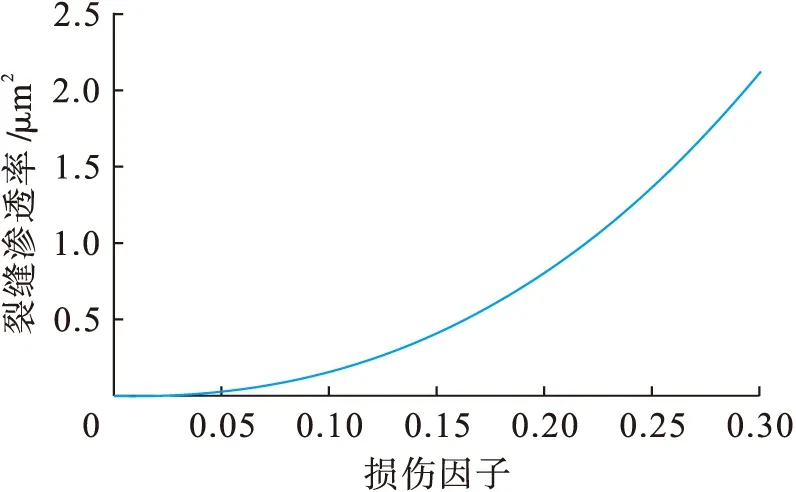
图3 损伤与裂缝渗透率关系Fig.3 Relationship between damage and fracture permeability

采用有限元软件ABAQUS计算塑性损伤模型，采用有限差分软件CMG计算油藏渗流模型.迭代耦合计算过程中，渗流模型的求解领先损伤模型一个时间步，求解步骤为：首先求解渗流模型，获得当前时间步的压力和饱和度等渗流参数；根据压力和饱和度计算地层应力分布；求解损伤模型，获得损伤因子分布；根据损伤因子获得新的裂缝渗透率，求解下一时间步的渗流动态，直至结束.

储层生产初期(第100 d)时地层中损伤因子分布如图4所示.蓝色区域边角处为注入井位置，对角处红色区域顶点处为生产井位置，可以看出生产初期生产井周围地层的损伤因子下降，但注入井周围的损伤因子稍微上涨，这是由于注水引起局部地层压力增加，导致地层裂缝张开，损伤上升.随着生产时间的增加，地层中流体不断被采出，地层孔隙压力逐渐减小，有效应力增加，整个地层的损伤因子都在下降，损伤因子分布如图5、6所示.

图4 100 d时损伤因子分布Fig.4 Distribution of damage factor for 100 d

注入井与生产井处的损伤因子和裂缝渗透率变化如图7所示.由于注水减缓了注入井周围地层压力下降的趋势，裂缝闭合程度减小，因此，注入井周围的损伤和裂缝闭合程度都低于生产井，生产初期裂缝变化趋势较为缓慢，随着时间的增加，裂缝闭合幅度增加.

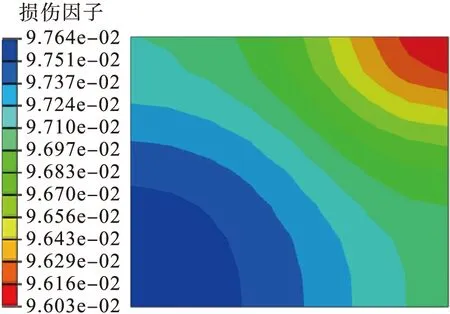
图5 400 d时损伤因子分布Fig.5 Distribution of damage factor for 400 d

图6 700 d时损伤因子分布Fig.6 Distribution of damage factor for 700 d

图7 注入井和生产井周围损伤与裂缝渗透率Fig.7 Damage and fracture permeability around injection and production wells

为了研究地层裂缝变化对储层生产动态的影响，图8给出了由不考虑裂缝变化的常规模拟方法和考虑流固耦合裂缝变化的耦合模拟方法获得的储层压力分布.生产初期(100 d)储层整体压力基本相同.随着开采进行，裂缝渗透率降低增大了地层的压力梯度，常规模拟和耦合模拟计算得到的地层压力出现明显差异.注入井周围地层压力比生产井周围地层压力大，裂缝渗透率减小幅度低，导致生产井周围压降幅度大于注入井.

图9对比了常规模拟和耦合模拟的日产油量和累计产油总量.生产初期，日产量相差不多，随着生产进行，裂缝闭合，渗透率降低，增加了地层中流体流动的阻力，耦合模拟得到的日产油量下降趋势逐渐增加，累计产油总量明显降低.700 d后，生产井日产量耦合模拟下降65%，常规模拟只下降54%，累计产量耦合模拟只有常规模拟的78%.因此，裂缝闭合是导致裂缝性储层产量下降的重要因素.常规的油藏数值模拟方法会明显高估裂缝性储层的生产能力，在裂缝性储层数值模拟时，应考虑裂缝渗透率变化对产量的影响.

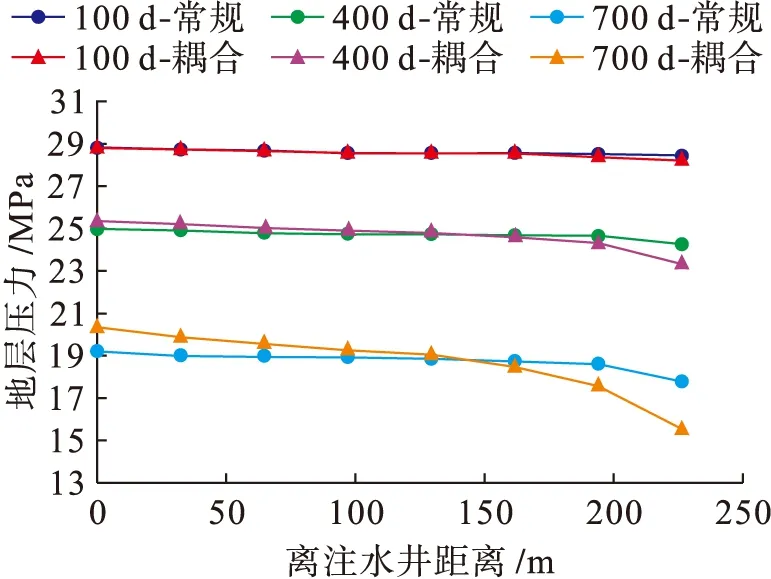
图8 储层压力分布Fig.8 Pressure distribution of reservoir

图9 裂缝性储层产量Fig.9 Oil yield of fractured reservoir

5 结 论

本文采用塑性损伤模型，结合双重孔隙介质模型建立了裂缝性储层流固耦合数值模拟方法.使用损伤变量从数学上表征储层裂缝的渗透率，并利用迭代耦合方法计算流体渗流与岩石变形的耦合行为，模拟了裂缝性储层注采过程中的损伤演化和裂缝变形，研究了裂缝变化对油田生产动态的影响.模拟结果表明，油田开采过程中，地层裂缝逐渐闭合，渗透率降低，生产井附近裂缝渗透率降低程度大于注入井.裂缝渗透率降低对裂缝性储层生产具有负面影响，且是导致裂缝性储层产量下降的重要因素.不考虑裂缝变化的常规油藏数值模拟会高估油田生产能力，因此，裂缝性储层数值模拟时应考虑裂缝变化对产量的影响.