基于ZEMAX二氧化硫荧光采集光路的设计仿真

刘杰辉，李 鑫

(河北工程大学 机械与装备工程学院，邯郸 056038)

引 言

迄今为止，空气中二氧化硫的污染相对较为严重。人们在关注经济快速发展的同时也开始注重环境的保护。为了更加准确地了解到我国现在环境的污染状况,研制出能够实时在线检测的二氧化硫仪器势在必行。二氧化硫检测仪的原理是紫外荧光法，这是国家标准GB3095-2012中所规定的检测方法。紫外荧光法可以突破传统化学检测方法的种种缺陷，能够更准确地检测二氧化硫[1]。其原理是：SO2气体被波长范围为220nm附近的紫外光照射时，SO2分子就从基态转化为激发态，激发态的SO2是不稳定的，在其转化为基态的时候产生荧光，对其产生的荧光进行收集利用就可以得出空气中二氧化硫的含量[2]。荧光强度和光电倍增管输出的电信号除去一些干扰以后是呈线性关系的。所以，对光电倍增管输出的电信号进行一系列的放大、滤波等处理后，就可以得出二氧化硫的具体含量。紫外荧光法与传统方法相比存在许多优势，不仅能够在线实时检测，并且可以降低误差，提高检测的准确性。利用荧光光谱法对SO2含量进行检测的过程中，最小的检测范围已经达到了10-9数量级[3]。

目前研发的二氧化硫检测仪器采用的荧光采集光路是利用双凸透镜对荧光点光源进行了汇聚。该系统存在很多不足，不仅光线的汇聚效果不理想、存在较大像差,而且由于透镜的焦距长导致增大了荧光采集光路的长度[4]。基于上述光路的种种缺陷，本文中提出了一种新型对称式平凸结构，可以有效解决上述光路存在的问题，并通过ZEMAX仿真验证了对称式平凸结构的合理性。

1 理论依据

在实际运用中几乎不可能达到完美的成像质量。由球差效果图可知，光线并不在光轴上聚于同一个焦点，而在镜头边缘入射的光线与光轴的交点要比接近光轴入射的光线与光轴的交点离镜头的距离近，如图1所示。这是很常见的像差之一，称之为球差[5]。球差的大小取决于光线在入瞳上的高度。消除球差可以采用非球面，非球面虽然不能完全消除像差，但可以使像差达到最小[6]。减小球差的另外一个方法是将光焦度进行分解[7]。

Fig.1 Effect of spherical aberration

1.1 非球面消球差

在光学系统中，想要将球差减小到最小，首先应该明白球差产生的原因是什么。从理论上来说，如果一个系统中不存在球差，那么系统中任意光线的光程是永远相等的。

在建模过程中首先需要建立一个适当的坐标系。在光学系统中，取其中一条单面子午截线的对称中心作为原点建立直角坐标系。所以，无限远处的点光源发出的平行光照经过该系统后，选取经过单面子午截线上点P(x，y)的远轴光线和近轴光线作为研究对象，如图2所示。按照上述理论可知，近轴光线和远轴光线的光程应该相等。远轴光线经过点P(x，y)交x轴于点b，交y轴于点a，近轴光线是与x轴重合的光线，与远轴光线共同交于点b；n和n′分别代表的是空气的折射率和光学系统的折射率；xP和yP也就是P点的坐标值；f′是近轴光线经过的路程。对于任意一个给定的光学系统，如果这个系统不存在球差，那么一切经过这个特定光学系统的光线都应该在光轴上交于同一个点。也就是说，这两条光线的光程是恒等的。远轴光线光程的具体公式是：

Fig.2 Imaging of infinite object point due to single refractive surface

(1)

近轴光线光程则为n′f′，因此对于任意子午截线上的点，光程恒等的曲面是：

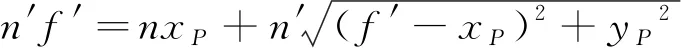
(2)

化简得:

(3)

由(3)式可得：当f′一定时,n′>n为椭圆；n′/n=-1为抛物面；n′/n=1为平面(yP=0)。

除去n′/n=-1的情况后，该方程仍然是二次的，所研究的光路系统n和n′分别代表空气和石英的折射率，所以不符合上述条件。即将球面透镜非球面化以后可以达到消球差的目的。

非球面上各个点的曲率半径均不相同，其面形由高次多项式决定。从光学角度而言，非球面指折射面为球面以外的所有面。设计者可以通过改变其曲率来获得理想的成像质量。

1.2 双球面折射系统光焦度

图3为双球面折射系统图。图中,u1表示入射张角，u2表示出射张角，h为光学系统入射点到主轴的距离，n1，n2和n3分别表示不同介质的折射率。由图3可知，双球面系统光焦度F的表达式为：

(4)

式中,O1折射面的光焦度为F1,O2折射面的光焦度为F2；d为两个折射面之间的距离；r为曲率半径，光从左向右传播，以球面和主光轴的交点为准，球面的球心在该点以左，则曲率半径为负，反之，球心在在该点以右，则曲率半径为正。r1为第1个折射面的曲率半径，r2为第2个折射面的曲率半径。

Fig.3 Bispherical refraction system

如果是双凸透镜系统，石英透镜的折射率要大于空气折射率，则n1=n3代表空气中的折射率；n2表示石英透镜的折射率；曲率半径r1=-r2，且r1>0,那么化简可得：

(5)

同理,如果是对称式平凸透镜，则n1=n3代表石英透镜的折射率；n2表示空气的折射率；曲率半径r1=-r2，且r2>0,化简得：

(6)

由于两个光路都对光线进行了汇聚，所以光焦度F的值应该大于0。在本次设计过程中，对称式平凸透镜和双凸透镜的曲率半径相同；材料和波长相同，所以空气和石英透镜的折射率是相同的；双凸透镜的d值明显大于对称式平凸透镜的d值，所以F对称式平凸>F双凸。由理论可知，在光焦度大于0的情况下，F的值越大，汇聚效果越好。

因为非球面价格昂贵、没有足够的精度以及随温度变化的不稳定性，故其在实际领域里难以普及。所以减少像差可以在光学系统中增加光学元件，光焦度可以在几个元件间进行分解，这样可以降低每个表面上的入射角度，从而达到的目的。

2 ZEMAX优化仿真分析对比

2.1 光路对比

目前的二氧化硫监测仪器采用一个双凸透镜和一个滤光片组成荧光采集光路，如图4所示。由荧光发出的点光源经过双凸透镜进行汇聚，在通过滤光片滤光后入射到探测器上。为了减少像差而采用的对称式平凸结构，在两个透镜中设有可以限制较大入射角光线的隔镜环，在探测器前面设有滤光片，如图5 所示。将以上两种光路运用ZEMAX仿真进行对比。

Fig.4 Fluorescence acquisition system with dual convex lens

Fig.5 Acquisition system with symmetrical plano-convex lens

2.2 仿真及优化

设计或者优化任何一个光路结构，都有特定的要求，例如焦距、入瞳直径、视场、波长、材料、分辨率、渐晕和调制传递函数(modulation transfer function,MTF)等，根据不同系统的简易程度要求也各不相同[8]。由于荧光波段在330nm强度最高，所以设定的波长是330nm；在240nm～420nm的波长范围内，石英透镜对二氧化硫发射出荧光的透过率比普通玻璃透镜大很多，所以材料选用石英玻璃；其中视场为1，入瞳直径为20mm，分辨率为2048×2048。

在确定光路的具体路径后对两个光路进行局部优化，得到最小的光斑半径。ZEMAX中局部优化算法有阻尼最小二乘法(damped least squares,DLS)和正交法(orthogonal descent,OD)，在纯非序列系统中由于探测结果是在被像素化的探测器上获得，其评价函数是不连续的，使用阻尼最小二乘法的运用效果并不理想，故采用正交法更为合适。

正交法对变量进行标准化，并对解空间进行离散化抽样来降低评价函数，并不计算评价函数的数值导数。相比较于阻尼最小二乘法，正交法对含有噪声评价系统的函数(比如非系列系统)更有优势。正交法能够很好的完成照度最大化、亮度增强以及均匀化的优化问题。图6即为采用正交法后的优化结果。可以看到，将光斑半径明显减少达到了预期的优化效果。

Fig.6 Orthogonal optimization diagram

2.3 仿真结果分析对比

以下是运用ZEMAX对两种光学系统进行仿真优化后的具体对比。

(1)首先进行两种系统的光路仿真，光线从光源发出经过透镜后汇聚于探测器上，如图7和图8所示。对比两种光路的非序列结构(non-sequential compoonent,NSC)阴影模型图，观察到图7中经过对称式双凸透镜入射到探测器上的光线较图8中双凸透镜的汇聚效果更加集中，光线散射程度更小。对称式双凸透镜光路设计更加合理。

Fig.7 NSC shadow model diagram of double convex lens

Fig.8 NSC shadow model diagram of symmetrical plano-convex lens

(2)为了更好地比较两种光路汇聚效果，设置光线条数为1000，跟踪分析光线探测器，得到探测器视图，如图9和图10所示。对比两种光路的峰辐强度、总功率以及撞击次数(见表1)[9]，发现优化后的峰辐强度达到了219.41W/cm2,是之前的3倍，总功率达到了0.35410W。由此可见，对称式平凸透镜的汇聚效果要比双凸透镜的汇聚效果好,即在相同的荧光强度下，对称式平凸透镜可以更好地进行汇聚，以便于接收器接收到更多的信号[10]。

Fig.9 View of double convex lens detector

Fig.10 View of symmetrical plano-convex lens detector

Table 1 Comparison diagram of probe view data

(3)进行点列图仿真分析。在理想状态下，由一个点光源发出的所有光线在通过一个比较理想的光学系统之后，会汇聚到一个点，这就是这个物点的像点。[11]但是在实际光学系统的应用过程中，因为不可能不存在像差，所以经过光学系统用探测器查看后会形成一个光斑，称其为弥散斑。探测器上的视图称为点列图。

点列图实际代表的是光斑分布的密集状况，越密集说明成像质量越好。衡量点列图光斑分布情况可以用几何最大半径值(geometric maximum radius,GEO)和均方根(root mean square,RMS)半径值来进行表示[12]。几何最大半径值就是以参考光线点为中心，包含所有光线的最大圆的半径，而均方根半径则是每条光线交点与参考光线点的距离的平方，除以光线条数后再开方[13]。也就是说均方根半径值反映了光能的集中程度，几何最大半径反映了像差的最大值。这两个的值越小，说明成像质量越好[14]。

图11和图12是两种系统光学仿真后得到的点列图。由图11可知,对称式平凸透镜点列图的GEO为1182.71μm，RMS为671.872μm。图12中双凸透镜点列图的GEO为6798.75μm，RMS为2501.57μm。比较两种系统数据，对称式平凸透镜的几何最大半径值和均方根半径值远小于双凸透镜点列图的值，两个系统的几何最大半径之比为：1182.71μm/6798.75μm=17%。所以对称式平凸透镜的弥散斑直径更小，成像质量更佳[15]。

Fig.11 Point series diagram of double convex lens detector

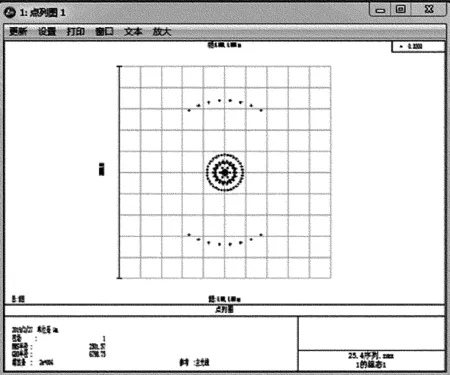
Fig.12 Point series diagram of symmetrical plano-convex lens detector

经过上述对比不难发现,从NSC阴影模型图中光线的汇聚、探测器探测视图以及点列图中弥散斑半径大小均可得到对称式平凸透镜的成像质量要优于一个双凸透镜的结果。

3 结 论

运用光学仿真软件ZEMAX，在目前监测仪器的荧光采集光路基础上对其进行了优化设计。对比探测视图和点列图后发现优化后的峰辐强度是之前的3倍，总功率达到了0.35410W，有效半径和均方根半径都大幅度减小，达到了优化的目的。在与光源距离相同的条件下，对称式平凸透镜相较于双凸透镜不仅结构简单、安装方便、光能损失较小而且成像质量相对较好。因此，对称式平凸透镜结构能够很好地应用于荧光的检测。