混合空气悬架多工况阻尼自匹配协调控制
2020-04-10
(西安科技大学 机械工程学院,陕西 西安 710054)
引言
空气悬架不仅具有良好的非线性刚度特性,而且能根据实际需要调节车身高度,因而对于汽车行驶平顺性以及行车安全性都具有重大意义[1]。
传统空气悬架一般由空气弹簧与减振器并联而成,近年来随着空气悬架理论模型研究的成熟,对空气悬架的控制尤其是对于空气悬架刚度与减振器阻尼的匹配控制问题,越来越成为国内外学者研究的重点[2-4]。MOSHCHUK NIKOLAI等[5]进行了刚度或阻尼可调的半主动空气悬架建模分析以及试验研究。HYUNSUP KIM等[6-7]将实车车身高度与车身姿态同时控制,并采用滑模控制策略完成车身高度模式之间的准确切换。汪少华等[8]同时考虑了直线行驶工况和转向行驶工况,研究了半主动空气悬架混杂系统的多模式切换控制,实现了弹簧与阻尼的解耦,改善了空气悬架的各项动态性能。
上述研究均是在匀速工况下进行的,没有考虑行驶工况对悬架性能的影响。而汽车行驶是一个复杂多变的过程,单一工况的研究并不具有代表性。本研究针对这一问题,提出一种基于空气弹簧和直线电机作动器的混合空气悬架结构,根据不同行驶工况的要求设计混合空气悬架多模式阻尼自匹配的控制策略,并进行仿真分析和台架试验。
1 混合空气悬架原理与模型
混合空气悬架系统结构如图1所示,主要由空气弹簧系统、直线电机作动器等部分组成。其中空气弹簧系统由空气弹簧、空气压缩机、储气罐、电磁阀控制器及传感器组成。直线电机作动器由直线电机、功率模块电路、控制器及相应的信号检测装置组成。
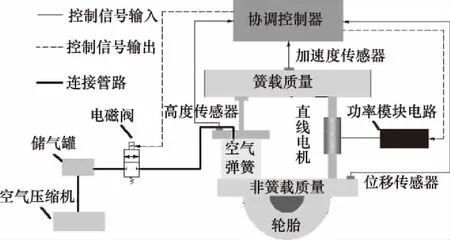
图1 混合空气悬架结构图
混合空气悬架的工作原理为:根据汽车行驶工况的不同,控制器ECU控制空气弹簧系统中的电磁阀的开闭状态实现对空气弹簧充放气,根据高度传感器的输入信号使弹簧处于相应的工况高度模式;同时,车轮受到不平路面的振动激励,车身产生振动,安装的加速度传感器和位移传感器将采集到的信号输入给控制器,控制器根据控制算法计算出相应高度模式下理想阻尼力,输出控制信号对直线电机进行阻尼系数的自适应匹配。
2 混合空气悬架动力学模型的建立
2.1 1/4车辆悬架动力学模型
根据图2利用牛顿运动定律,可以得:
(1)
式中,ms—— 簧载质量

K—— 空气弹簧刚度,其值是可变的
cg—— 可变阻尼系数
mu—— 非簧载质量

Kt—— 轮胎刚度
xq—— 路面输入
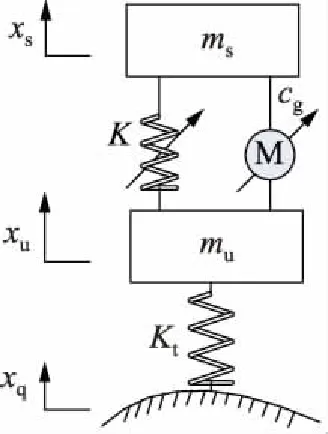
图2 二自由度悬架动力学模型
2.2 空气弹簧数学模型
图3为空气弹簧受力图,其有效刚度在汽车行驶过程中是动态变化的[9-10]。
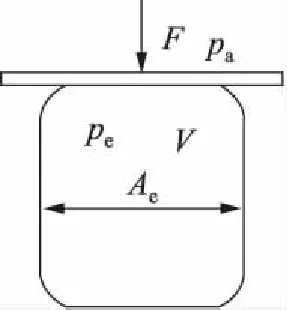
图3 空气弹簧受力图
根据图3,空气弹簧弹性力可表达为:
F=(p-pa)Ae=peAe
(4)
假设空气弹簧内的气体为理想气体,根据理想气体状态方程则有:
(5)
式中,F—— 空气弹簧弹性力
pa—— 大气压力
p—— 气囊内气体绝对压力
Ae—— 空气弹簧有效面积
p0—— 气囊内初始气体压力
pe—— 气囊内气体相对压力
V—— 空气弹簧有效容积
κ—— 热力学指数
(6)
(7)
2.3 直线电机数学模型
直线电机可用作电动机亦可用作发电机。假设所研究的直线电机为理想发电机,则发电机产生的电压可表达为[11-12]:
(8)
电机发电阻力可表示为:
Fg=ki·i
(9)
(10)
式中,ke—— 发电机反电动势系数
ki—— 电机的推力系数
i—— 电机线圈电流
Fg—— 电磁阻尼力
r—— 电机线圈内阻
R—— 可变电阻
3 混合空气悬架多工况阻尼自匹配协调控制策略
3.1 多工况阻尼自匹配协调控制原理
汽车行驶过程是一个复杂的动态过程,会根据行车环境在不同工况下进行转换,所以在对汽车性能进行研究时,需要考虑汽车的行驶工况[13]。
混合空气悬架多工况阻尼自匹配协调控制:以优先控制空气弹簧高度模式为原则,根据行驶工况对空气弹簧多工况模式的控制和在各个模式下根据悬架动态响应反馈的直线电机阻尼力自匹配。其控制框图如图4所示。
控制器通过车速信号对行驶工况进行判别,从而确定空气弹簧的高度模式,由于各高度模式下对悬架系统控制要求的侧重不同,所以不同模式下根据悬架动态响应的反馈,采用混合天棚-地棚控制算法对所需理想阻尼力进行匹配,将理想阻尼力输入直线电机作动器,调节可变电阻控制直线电机可调电磁阻尼力,并作用于悬架系统。

图4 混合空气悬架多工况阻尼自匹配协调控制框图
3.2 空气弹簧多工况模式分析
不同的承载和行驶路况,设置不同的高度模式,选择合适的车辆行驶高度,可以有效提升车辆性能,根据行驶工况对空气弹簧多工况模式进行分析,其对应关系如图5所示。
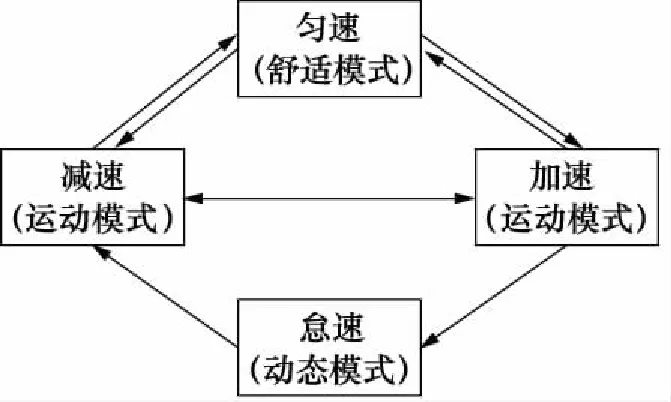
图5 各行驶工况与悬架模式之间的关系
1) 舒适模式
舒适模式是指汽车在匀速工况下,基于固有频率与悬架高度的关系确定弹簧高度,以保证汽车的行驶平顺性。悬架的固有频率是衡量汽车平顺性的重要参数,它由悬架刚度和悬架弹簧支承的质量(簧载质量)所决定[14-15]。人体所习惯的垂直振动频率约为1~1.6 Hz。车身振动的固有频率应接近或处于人体适应的频率范围,才能满足舒适性要求。悬架固有频率为:
(11)
舒适模式以车身加速度为主要指标,适当降低悬架的固有频率f可以明显减小车身加速度,改善汽车的平顺性。对式(7)中空气弹簧气体柱H的单位由m转换为mm,任意状态下空气悬架的固有频率:
(12)
图6为混合空气悬架的固有频率与气囊初始气压和空气弹簧高度的关系图,其中X坐标轴表示空气弹簧高度,Y坐标轴表示气囊初始气压,Z坐标为悬架固有频率。在相同初始气压状态下,悬架的固有频率随着空气弹簧高度H的增加而减小,在同一高度下,悬架的固有频率随着初始气压的增大而增大。因此对空气弹簧高度以及气囊内初始压力进行控制,可以使悬架固有频率保持在所需范围内或实现悬架的等频振动。
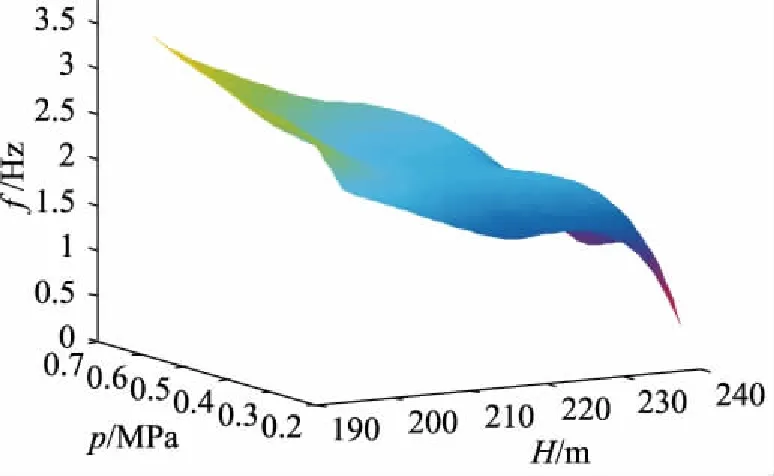
图6 固有频率与气囊初始气压和弹簧高度的关系
2) 运动模式
运动模式是指汽车在加/减速工况下,基于车身高度与悬架高度之间的变化关系确定弹簧高度,以保证汽车的安全性。当汽车急速起步或加速行驶时,由于惯性力及驱动力的作用会使车尾下蹲,产生后仰现象;当汽车在高速行驶中急刹车时,由于惯性力和轮胎与地面摩擦力的作用会使车头下沉,产生制动点头现象。不管是加速后仰现象还是制动点头现象都会对行驶安全性和乘坐舒适性造成不利的影响。
悬架高度直接影响车辆质心高度,汽车悬架越高,质心就会越高。在有惯性力的情况下,各车轮上的受力变动量就越大。适当降低汽车的质心高度可以增大汽车的抓地性降低轮胎动载,提高汽车的安全性。质心高度与悬架高度之间存在关系式:
(13)
ΔH=Δhs
(14)
式中,hg—— 整车质心高度
hs—— 簧载质量质心高度
hu—— 非簧载质量质心高度
ΔH—— 悬架高度变化值
Δhs—— 簧载质量质心高度变化值
3) 动态模式
动态模式是指汽车处于怠速工况时,怠速工况分为驻车怠速和行车怠速,在该模式下悬架高度保持前一时刻弹簧高度状态不变,即混合空气悬架处于动态变化过程。
3.3 直线电机阻尼自匹配分析
直线电机的阻尼自匹配是指在混合空气悬架多工况模式的基础上,根据各个工况模式下悬架的动态响应反馈基于参考模型对不同模式下所需阻尼力自动匹配的控制。
由空气弹簧多工况模式分析可知,舒适模式和运动模式分别以乘坐舒适性和行驶安全性为主要评价指标,即在不同模式下分别对车身加速度和轮胎动载荷进行控制。由于在改善簧载质量振动特性的同时会在一定程度上恶化非簧载质量的振动特性,因此理想阻尼力参考模型采用混合天棚-地棚控制。

图7 混合天棚-地棚控制悬架原理图
图7为混合天棚-地棚控制悬架的原理图。天棚控制算法是在车体和假设天棚之间安装1个阻尼器,该阻尼器的阻尼系数称为天棚阻尼系数。地棚控制算法和天棚控制算法的控制原理基本相同,不同的是天棚控制直接作用在簧载质量上能有效抑制车身加速度,而地棚控制是直接作用于非簧载质量上,对轮胎动载荷有更好的改善作用。混合天棚-地棚控制综合两者优点,兼顾了汽车的乘坐舒适性和行驶安全性。混合天棚-地棚控制的理想阻尼力为:
F′=βFsky+(1-β)Fgnd
理想天棚阻尼力和理想地棚阻尼力分别为:
(15)
(16)
由式(10)、式(16)和式(17)可以得到直线电机作动器的可变电阻值为:
(17)
(18)
最终可得到直线电机作动器阻尼力自匹配时可变电阻值为:
R′=βRsky+(1-β)gnd
(19)
本研究着重考虑匀速工况和加/减速工况,所以调节因子β的取值为:舒适模式β=0.65;运动模式β=0.45。
4 仿真分析
为了验证混合空气悬架结构以及多模式阻尼自匹配协调控制的效果,本研究利用Simulink软件建立模型进行仿真分析。该悬架系统的主要参数如下:ms=320 kg,mu=30 kg,ke=68.4,Kt=150000 N/m,ki=25π,r=0.003 Ω,α=0.0186,Ae0=0.0381 m2天棚阻尼系数csky=2000 N·s/m,地棚阻尼系数为cgnd=2400 N·s/m。
4.1 各模式下的仿真
为了验证不同工况模式下混合空气悬架的效果,分别在舒适模式状态和运动模式状态下对悬架动态响应进行仿真分析,并与被动悬架以及传统空气悬架进行对比,此时直线电机作动器的电磁阻尼力为固定值。其仿真结果如图8~图10。
表1 悬架响应的均方根值
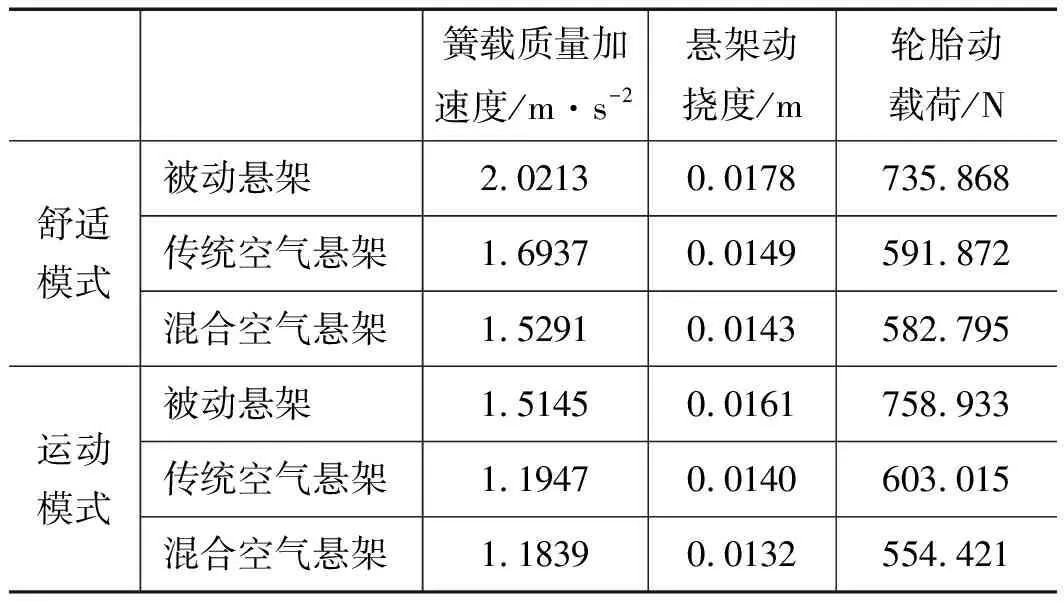
簧载质量加速度/m·s-2悬架动挠度/m轮胎动载荷/N舒适模式被动悬架2.02130.0178735.868传统空气悬架1.69370.0149591.872混合空气悬架1.52910.0143582.795运动模式被动悬架1.51450.0161758.933传统空气悬架1.19470.0140603.015混合空气悬架1.18390.0132554.421
由图8~图10、表1可以得出,当悬架系统处于舒适模式状态下,混合空气悬架的簧载质量垂直加速度均方根值相比于传统空气悬架降低9.72%,相比于被动悬架降低24.35%; 悬架动挠度均方根值和轮胎动载荷均方根值与被动悬架相比分别下降19.66%和20.79%,相比于传统空气悬架改善较小。当悬架系统处于运动模式状态下,混合空气悬架的轮胎动载荷均方根值相比于传统空气悬架降低12.08%,相比于被动悬架降低27.02%;簧载质量加速度均方根值和悬架动挠度均方根值与被动悬架相比分别下降21.83%和18.01%,相比于传统空气悬架改善较小。
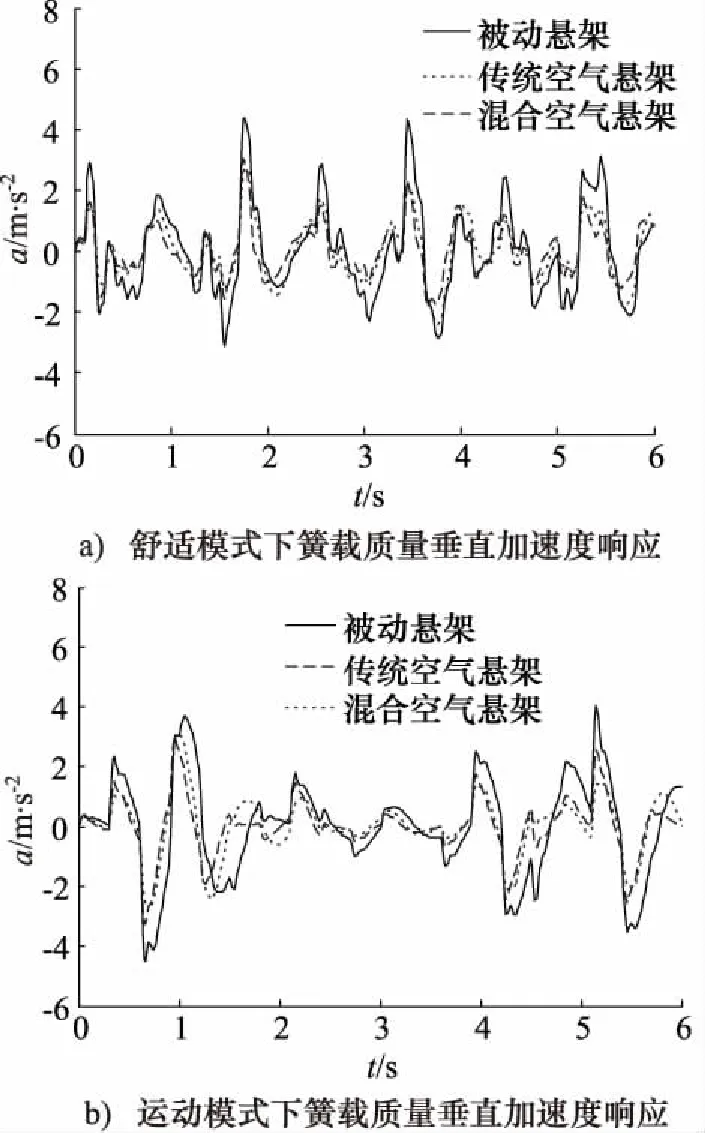
图8 簧载质量垂直加速度响应
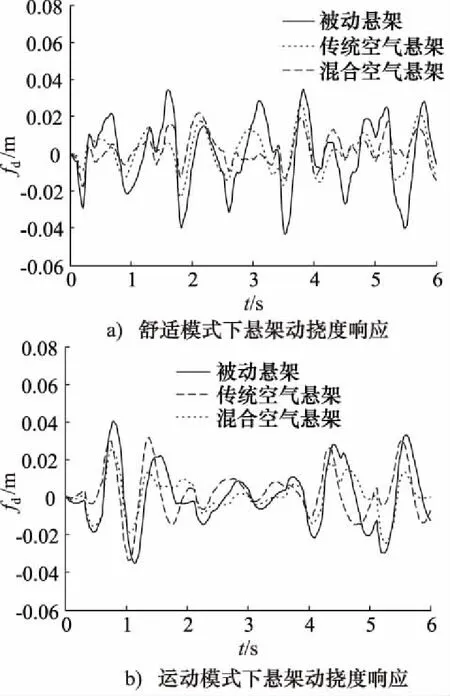
图9 悬架动挠度响应
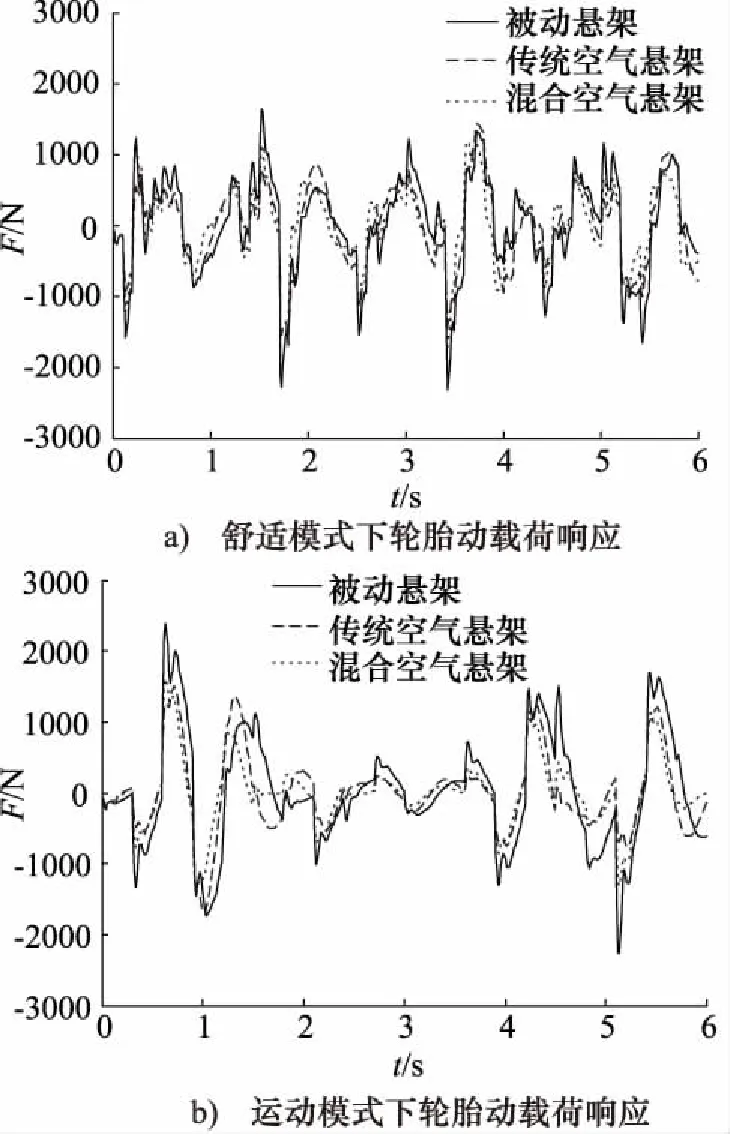
图10 轮胎动载荷响应
4.2 多工况阻尼自匹配协调控制仿真
为了验证多工况阻尼自匹配协调控制在不同行驶工况下的优越性,基于UDC(Urban Driving Cycle,城市循环)工况对比分析控制前后悬架的动态性能。利用Simulink软件中的Signal Builder功能模块,建立了不同循环单元的车速变化模型,如图11所示。

图11 模拟UDC工况车速变化模型
由于仿真时间较长,为清晰的显示各工况悬架动态响应情况,截取各工况模式下部分响应进行分析,如图12所示,0~1 s内车辆为怠速状态,1~4.5 s内车辆为加速状态,4.5~6 s内车辆为匀速行驶状态。
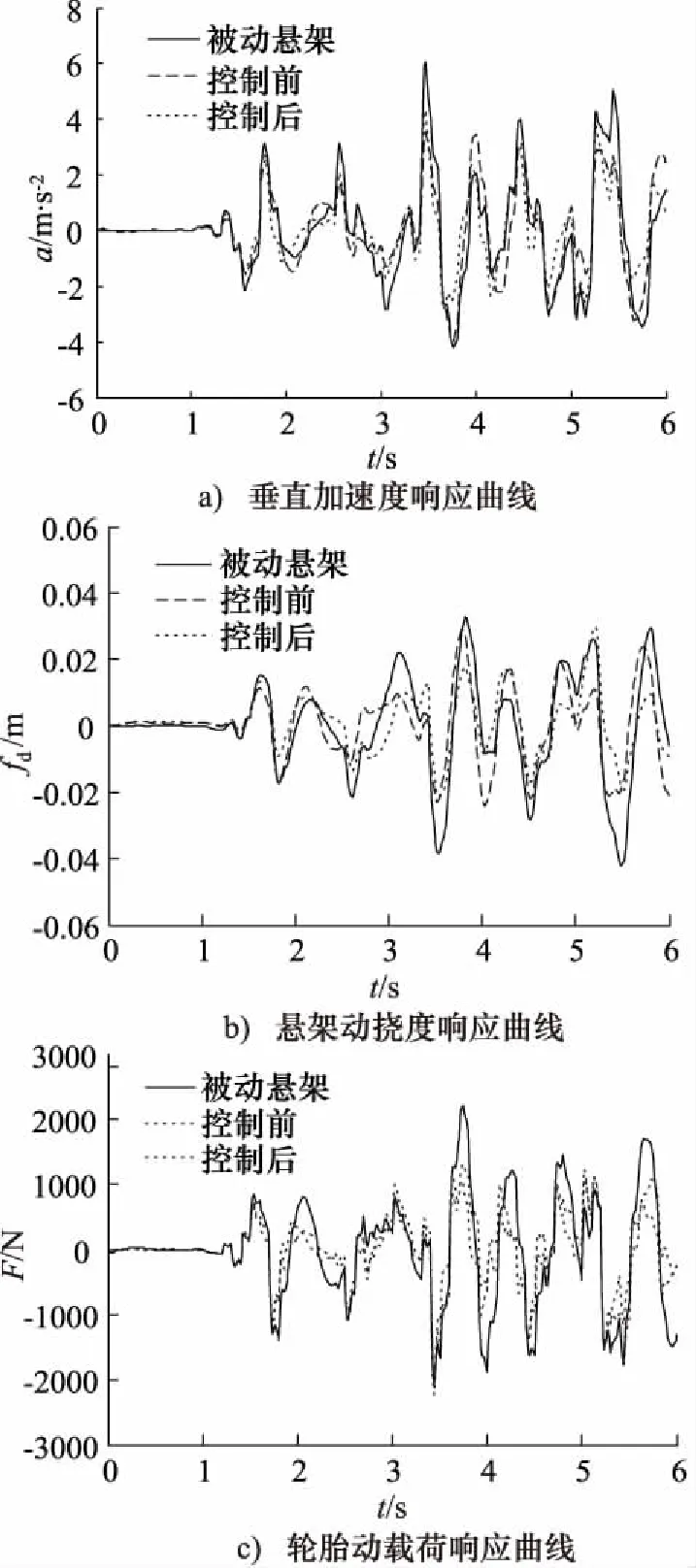
图12 UDC工况下仿真结果对比

表2 UDC工况下悬架响应的均方根值
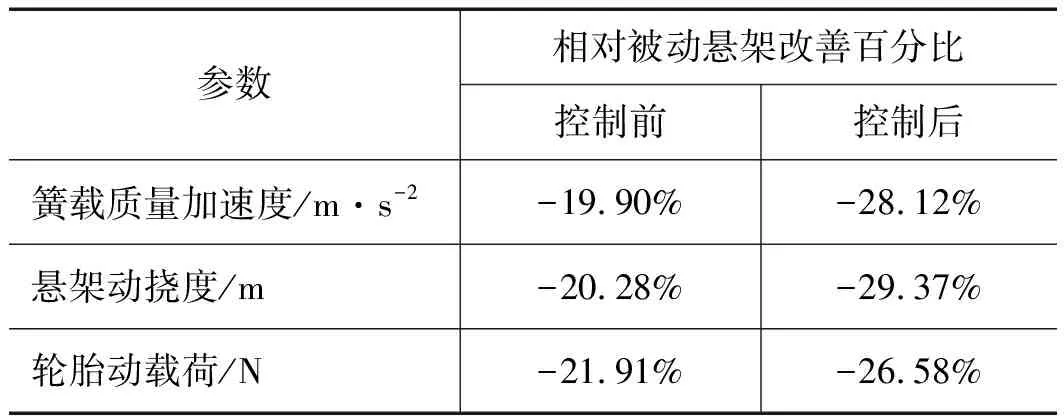
表3 仿真结果比较
由图12和表2可以看出,模拟UDC工况,混合空气悬架在多工况阻尼自匹配协调控制下悬架性能相比于被动悬架更大程度得到改善,其中车身垂直加速度的均方根值降低了28.12%;悬架动挠度的均方根值降低了29.37%;轮胎动载荷的均方根值降低了26.58%。
对悬架各指标在0~100 Hz进行α分析,结果如图13所示。

图13 悬架响应的频率特性分析
在低频区域,混合空气悬架多工况协调控制有效改善了垂直加速度和轮胎动载荷的频率特性,同时保证了低频振动时的车辆平顺性和行驶安全性,而悬架动挠度在低频区有一定程度的恶化,但其值也均在限定范围内。在中高频区域,各项指标均有一定程度的改善,反映出混合空气悬架多工况协调控制策略的有效性。
5 混合空气悬架台架试验
对混合空气悬架开展台架试验,验证多工况阻尼自匹配协调控制的有效性,其试验测试系统如图14所示。该系统主要由ES-6-230电动振动台、上下横梁、导向机构、DSP控制器、脉冲信发生器、数据采集与处理系统等组成。结合试验条件和验证目标,利用脉冲信号发生器输出脉冲信号模拟工况变化传给DSP控制器,在试验台上横梁处安装加速度传感器采集簧载质量加速度信号传给DSP控制器, DSP控制器根据设计的控制策略,改变空气弹簧工作模式并使直线电机

图14 混合空气悬架台架试验系统
输出作动力从而完成对悬架的控制。
由于受试验条件的限制,本次试验在幅值为30 mm、频率为3 Hz的正弦模拟路面激励下进行且忽略了怠速工况的影响,采样簧载质量加速度进行对比,试验结果如图15和表4。
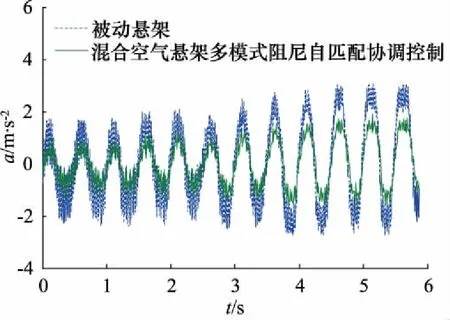
图15 试验条件下簧载质量加速度响应
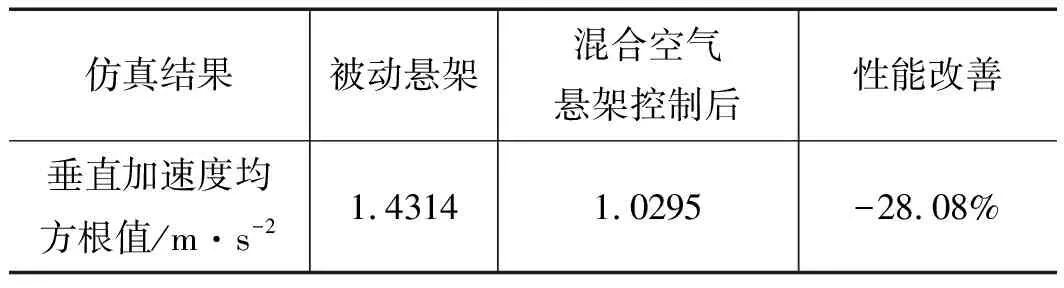
表4 簧载质量加速度均方根值
由图15与表4可知,采用多工况阻尼自匹配协调控制的混合空气悬架在正弦路面激励下,簧载质量加速度均方根值下降28.08%,验证了混合空气悬架多模式阻尼自匹配控制的有效性,能够有效减小簧载质量加速度,提高悬架的动态特性。
6 结论
(1) 提出了一种基于空气弹簧和直线电机作动器的混合空气悬架结构。结合空气弹簧的动刚度特性,基于不同行驶工况要求制定了空气弹簧的高度模式,以乘坐舒适性和行驶安全性为目标设计了混合天棚-地棚控制设计了直线电机多工况阻尼自匹配控制策略;
(2) 在UDC工况环境下进行了时域和频域仿真,结果表明:在UDC工况下,混合空气悬架中直线电机作动器能够有效自匹配各个模式下所需阻尼力,车身垂直加速度的均方根值降低了28.12%;悬架动挠度的均方根值降低了29.37%;轮胎动载荷的均方根值降低了26.58%;悬架的各项动态性能都明显改善;
(3) 以幅值为30 mm、频率为3 Hz的正弦激励作为路面谱输入,开展了混合空气悬架多工况自匹配协调控制台架试验研究,结果显示簧载质量加速度均方根值下降了28.08%,验证了仿真结果的正确性。
