基于遗传算法的气动肌肉T-S模糊逻辑控制优化
2020-04-10
(桂林航天工业学院 机械工程学院,广西 桂林 541000)
引言
气动肌肉执行器(PMA)是一种新型执行器,其执行方式比传统执行器(如电机和液压执行器)更安全,更兼容[1]。事实上,PMA已广泛应用于仿生学、医学、工业和航空航天领域[2]。然而,复杂的非线性动态特性使得PMA的轨迹跟踪控制非常困难,极大的限制了PMA的推广。
随着专家系统、模糊逻辑、遗传算法(GA)、神经网络等的发展[3-6],控制器的鲁棒性和控制精度得到很大提高,PMA所存在的控制问题也得到很好的解决。目前,PMA主要采用T-S模糊逻辑控制,其利用多个线性模型来局部逼近非线性模型。这些线性模型通过隶属函数连接,从而建立T-S模糊模型。从实现原理上来看,T-S模糊逻辑控制利用并行分布补偿理论(PDC)为每个线性模型设计局部控制器,然后对局部控制器的结果进行加权,并通过隶属度求和,得到最终控制信号。然而,考虑到T-S模糊逻辑控制器在很大程度上取决于模型参数的事实,由于参数的不确定性,T-S模糊逻辑控制器的性能会受到影响。
遗传算法(GA)是一种受生物进化规则启发的随机搜索算法,它模仿基因在生物繁殖、交叉和变异过程中的连续优化[7],从而获得了良好的全局优化能力。通过应用概率策略,遗传算法可自动获得并引导优化的搜索空间,并且可以自适应地调整搜索方向[8-9]。鉴于此,提出了一种基于遗传算法的T-S模糊逻辑控制器:首先,针对PMA的三元素模型,建立具有T-S模糊逻辑控制器;其次,利用遗传算法在实验过程中调整和优化控制器中使用的PMA参数,克服PMA参数不确定性的影响;最后,将传统的模糊逻辑控制(FLC),T-S模糊逻辑控制和经过GA优化后的T-S模糊逻辑控制进行比较,分析实验结果并验证所提出的控制策略的有效性。
1 气动肌肉动作的动力学模型
如图1所示为PMA的工作原理,当PMA充气时,橡胶气囊的体积增大,PMA在径向上变大,在轴向方向上缩短,从而产生升力以支撑目标物体。当PMA放气时,橡胶气囊的体积减小,PMA在径向上变小,在轴向上变长,从而使目标物体下降。
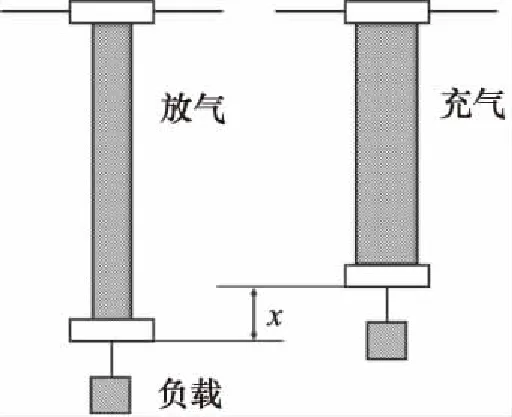
图1 PMA工作原理
由于PMA的多样性和复杂的动态特性,目前已知的PMA动态模型较多,使用D.REYNOLDS提出的PMA三元素模型[10-11],如图2所示。其中,F(p)为收缩元素,K(p)为弹簧元素,B(p)为减振元素,三元素模型中的PMA系统被认为是非线性摩擦,因此图2所示的动态方程如式(1)所示[12-13]:

(1)
式中,m为目标对象的质量;x为PMA收缩长度,x=0表示没有输入压力时PMA的初始位置;g为重力加速度;p为输入压力。3个系数和输入压力之间的函数为:

图2 PMA三元素模型
当输入压力p>p0时,
K(p)=K10+K11p
(2)
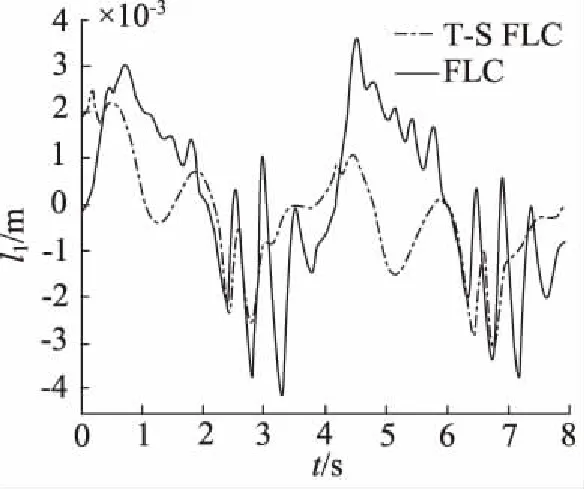
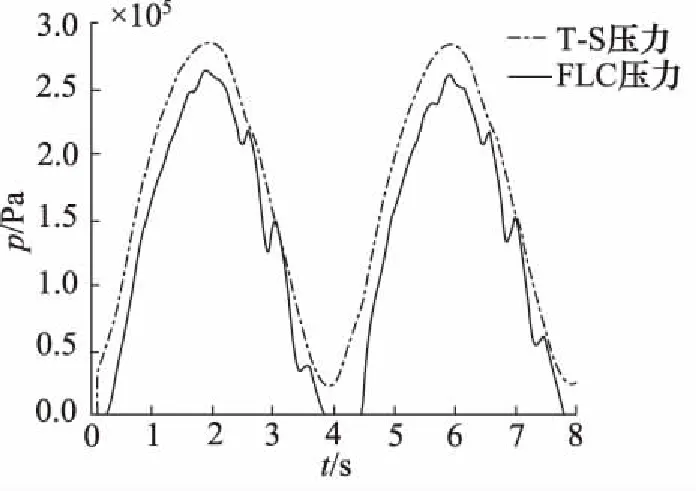
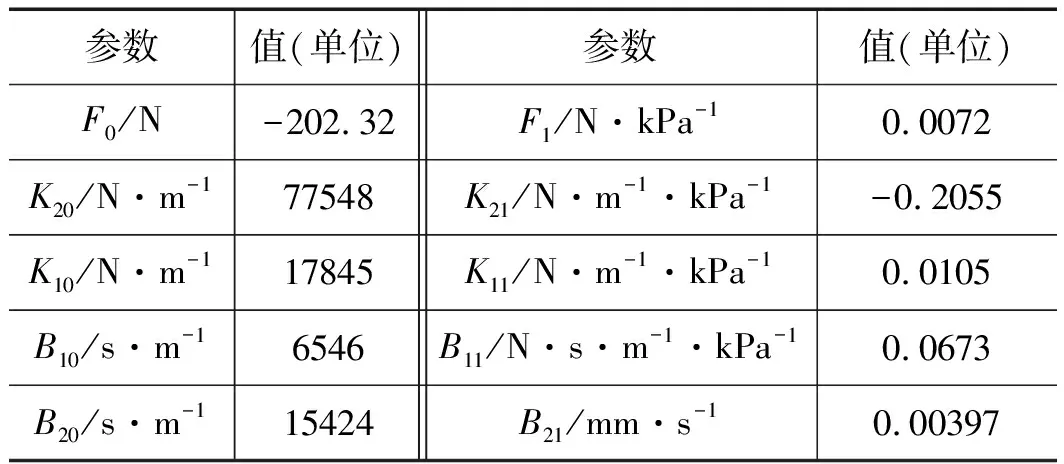
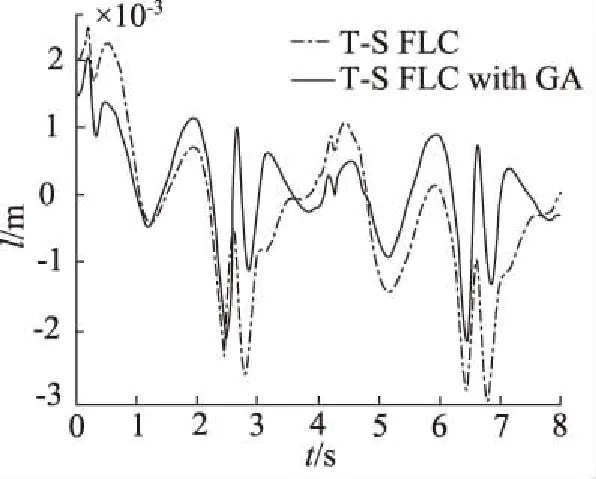
当输入压力p K(p)=K20+K21p (3) 充气时, B(p)=B10+B11p (4) 放气时, B(p)=B20+B21p (5) F(p)=F0+F1p (6) 其中,p0是输入压力的临界值。 (7) (8) 式(8)可以改写为: (9) (10) (11) (12) (13) 其中, 对于PMA而言,每个状态的差异只是状态矩阵Ai中的参数,因此可以通过仅设计一个控制器来控制PMA并调整其参数。PMA系统状态如式(14)所示。 (14) 其中,Ai和C为常数矩阵,输入矩阵B中的f(x1,x2)为状态变量的非线性函数。由函f(x1,x2)可知,系数B1和K1将随状态变量x1和x2而变化,根据参考信号,可以知道变量x1和x2的范围。因此可以得到非线性函数f(x1,x2)的范围,然后通过T-S模糊建模,可以将非线性子系统式(14)线性化。 PMA经过T-S模糊后的模型如式(15)所示: (15) 其中,i=1,2,3,4为4个子系统的数量,与T-S模糊模型无关,j为T-S模糊模型的数量。 为了更精确地表达非线性系统,设计了7个模糊规则wj(j= 1,2,…7),即: Rule 1: IFf(x1;x2) is aboutfmin, Rule 2: IFf(x1;x2) is aboutf2, … Rule 7: IFf(x1;x2) is aboutfmax, Aij,Bj和C为常数矩阵,其中: 其中,fmin为非线性函数f的最小值,fmax为最大值,其他5个矩阵B2~B6是fmin和fmax之间的分割点。 E=Xr-X (16) 为了将跟踪控制问题转化为稳定性控制问题,提出了一个误差系统,即: (17) 其中,λ(t)为控制信号,将式(15)和式(16)代入式(17)中,可得到: (18) 通过并行分布补偿(PDC)来控制误差系统的稳定性,可以得到反馈增益Hk并计算误差系统的控制信号如式(19): (19) 在得到控制信号λ(t)后,将式(19)带入式(17)可得: (20) 构造Lyapunov函数: V=E(t)TpE(t)>0 (21) 对Lyapunov函数进行求导即: 为了保证误差系统式(14)的稳定性,反馈增益Hk应满足以下线性矩阵不等式: (Ai-BjHk)Tp+p(Ai-BjHk)<0 j,k=1,2,…,7 (22) p>0 (23) 应用LMI工具箱,可以解决上面的不等式并得到误差系统的控制信号(21): (24) 最后,将式(24)代入式(18),即可得到PMA的控制信号u。 因为上部分中的控制信号u是通过PDC计算得到,而PDC中的控制器设计是为了解决不等式(22)和式(23)。因此系统矩阵Ai和输入矩阵Bj中参数的不确定性会影响控制信号并限制T-S模糊控制器的性能。为了使式(22)能够搜索到最佳参数,采用GA在线优化参数。如图3所示为GA算法流程图。 图3 GA算法流程图 T-S模糊控制器优化主要按照以下步骤: 步骤1:初始化阻尼系数函数B(p)中的参数B10,B11,B20,B21和弹簧系数函数K(p)中的参数K10,K11,K20,K21; 步骤2:使用MATLAB的LMI工具箱计算PDC中的反馈增益Hk; 步骤3:获取控制信号u并在实验中驱动该装置; 步骤4:根据实验中的累积误差计算适应度; 步骤5:选择最适合的个体并保存其控制数据; 步骤6:如果生成数量已达到目标数量,则转到步骤7,否则使用GA计算下一代并转到步骤2; 步骤7:获取最适合的数据作为在线优化的结果。 如图4所示为使用的PMA系统平台,该平台包括气动肌肉、力传感器、位移传感器、压力传感器、空气压缩机、电磁比例阀和xPC目标系统。其中,空气压缩机为PMA提供压力,以实现PMA作动。当PMA作动后,由压力传感器和移位传感器采集压强和位移数据,并将其传送给计算机。计算机在接收到压强和位移数据后,根据所设计的控制策略计算控制信号,并通过控制信号调节电磁比例阀的开度以控制输入压力,从而达到控制PMA运动的目的。如表1所示为PMA的初始参数: 图4 PMA系统平台 表1 PMA初始参数 将表1中的参数值代入式(21)和式(22),可以得到状态反馈增益Hk,子系统式(10)~式(13)的状态反馈增益如表2所示。参考轨迹参照D.Reynolds提出的PMA三元素模型,如式(25)表示,采样时间为0.0001 s。 yr(t)=0.0125-0.0125cos(0.5πt) (25) 实验中,将传统的无模糊逻辑控制(FLC)与T-S模糊逻辑控制(T-S FLC)进行对比实验。如图5所示为FLC和T-S FLC的PMA控制结果,相应的跟踪误差如图6所示,图7表示控制信号。从图5可以看出,T-S FLC曲线较FLC曲线更为平滑,即T-S模糊逻辑控制可以有效地克服跟踪控制期间的抖动。从图6可以看出,T-S FLC的跟踪误差范围为-2.9~+2.5 mm,FLC跟踪误差范围为-4.4~+3.7 mm,显然T-S FLC的跟踪误差要小于FLC。如图7所示为FLC和T-S FLC控制信号,可以看出T-S FLC的控制信号比FLC更为平滑并且无明显的冲击,因此T-S FLC可以获得更好的性能。 表2 状态反馈增益Hk 图5 FLC和T-S FLC的轨迹跟踪控制 图6 FLC和T-S FLC的跟踪误差 图7 FLC和T-S FLC控制信号 为了进一步提高T-S模糊逻辑控制器的精度,选择GA来优化控制器中使用的PMA参数,以克服参数不确定性的影响。如表3所示为GA优化后的参数,在GA优化过程中,将遗传代数设置为60,每个遗传代设置10个体。 表3 GA优化后的PMA参数 图8显示了优化过程中每一代的最佳适应度,很明显每代的最大适应度从30.8增加到51.54。如图9、图10所示为T-S FLC和经过GA优化后的T-S FLC的跟踪轨迹以及误差。从图10中可以发现,在优化PMA参数后,误差范围减小到-2.1~+2.05 mm,因此具有GA优化的T-S模糊逻辑控制器不仅可以克服抖振现象,还可以有效地降低误差。 图8 适应度 图9 T-S FLC和经过GA优化后的T-S FLC的跟踪轨迹 图10 T-S FLC和经过GA优化后的T-S FLC的误差 设计了一个基于PMA三元素模型的T-S模糊逻辑控制器,并引入基于遗传算法的在线优化策略,以降低PMA参数的不确定性对控制性能的影响。 (1) 所设计的T-S模糊逻辑控制器跟踪误差为-2.9~+2.5 mm,且曲线较传统的FLC更为平滑,即T-S模糊逻辑控制可以有效地克服跟踪控制期间的抖动; (2) 经过GA优化后的T-S FLC误差范围为-2.1~+2.05 mm,且优化后每代的最大适应度从30.8增加到51.54。结果表明,优化后的T-S模糊逻辑控制器不仅可以克服抖振现象,还可以有效地降低跟踪误差。2 基于遗传算法优化的T-S模糊逻辑控制
2.1 T-S模糊逻辑控制


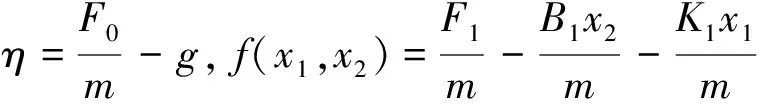
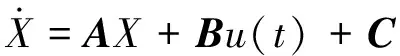
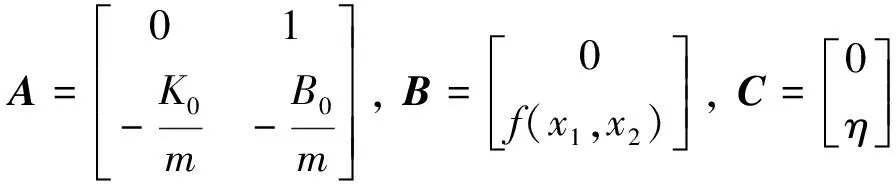
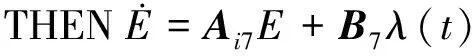

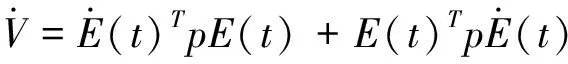
2.2 遗传算法的参数优化
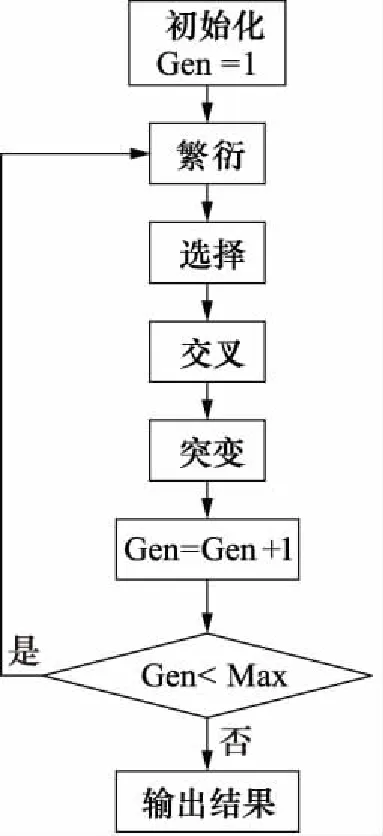
3 实验结果与讨论

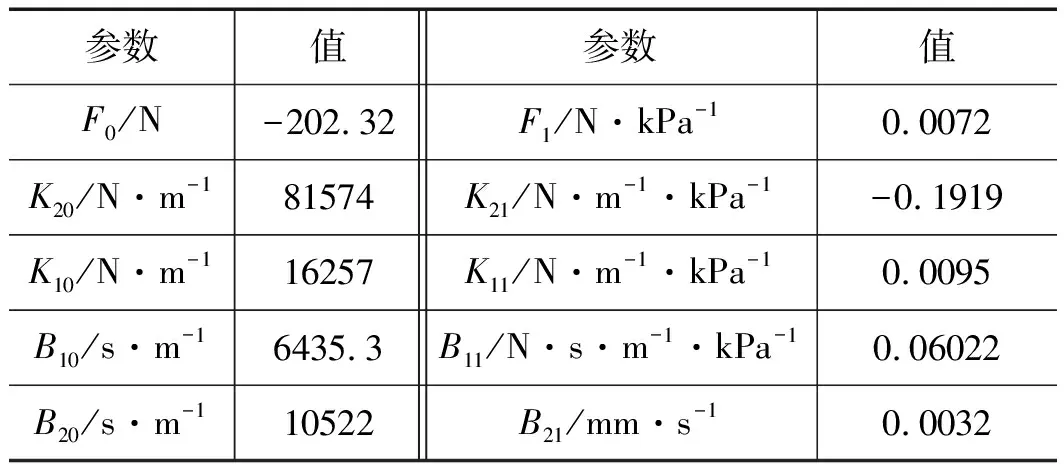




4 结论
