Decision-feedback subset aided multiple-symbol differential detection①
2020-04-10WangChanfei王婵飞XuYameiXuLei
Wang Chanfei (王婵飞),Xu Yamei,Xu Lei
(School of Computer and Communication,Lanzhou University of Technology,Lanzhou 730050,P.R.China)
Abstract
Key words:multiple-symbol differential detection (MSDD),decision-feedback (DF),decision-feedback subset,ultra-wideband impulse radio (UWB-IR),differential space-time block-code (DSTBC)
0 Introduction
Coherent detection is capable of achieving performance improvement with accurate channel state information (CSI)[1].However,collecting the perfect CSI is a demanding task.By contrast,the noncoherent receivers mitigate the problem of estimating CSI.Therefore,transmitted reference and differential detection get attention as noncoherent schemes in the single antenna system[2-4].Unfortunately,there is a wastage of the transmit power with the transmitted-reference,and the differential detection leads to bit error rate (BER) performance loss because the current symbol is detected using a noisy template of the received signal[5,6].Furthermore,multiple-symbol differential detection (MSDD) receives much research attention[7-9].
As a milestone for noncoherent detection,differential space time block-codes (DSTBC) becomes attractive[10,11],which is capable of improving the BER performance significantly compared to the single-antenna system.Furthermore,generalized likelihood ratio test based MSDD (GLRT-MSDD) and sphere decoding based MSDD have been conceived for the system[12].However,the aforementioned MSDD algorithms impose exponentially increasing complexity with the number of the observation window.Thus,the GLRT-MSDD and the sphere decoding based MSDD are impractical when the number of the observation window increases.Decision-feedback based MSDD (DF-MSDD) represents the computationally efficient algorithm with a low complexity[13].On the other hand,due to the inaccuracy of the estimated symbols on the edge of the observation window,there leaves a gap in terms of the BER performance between DF-MSDD and GLRT-MSDD.
Aiming to solve the problem of the performance loss caused by inaccurate detection on the edge of the DF-MSDD,in this work,a decision-feedback subset aided MSDD (DF-S-MSDD) is developed in the system with DSTBC modulation.More specifically,based on the DF-MSDD,a subset of decision-feedback symbols is employed,and the remaining symbols are optimized with GLRT-MSDD.The proposed DF-S-MSDD can simplify the classic exhaustive search as a detection with a lower computational complexity.Another benefit of the DF-S-MSDD is that,by getting rid of the inaccurate decision-feedback symbols on the edge of the observation window,it also enjoys a better BER performance when compared to the DF-MSDD.In general,the proposed DF-S-MSDD strikes an appealing performance-versus-complexity trade off.
It is worth emphasizing that the proposed DF-S-MSDD can be generalized in many noncoherent transmission with DSTBC modulation.Particularly,the ultra-wideband impulse radio (UWB-IR) signal contains lots of dense multi-paths components[14].Therefore,using the optimal coherent detector will increase the difficulty and cost of system implementation.Thus,noncoherent schemes become inevitable in UWB-IR system.Relying on this technique,the system description and simulation experiments are discussed in the UWB-IR system with DSTBC modulation.
The structure of this paper is formulated as follows.The system description is offered in Section 1.In Section 2,the GLRT-MSDD and DF-MSDD are introduced.The proposed DF-S-MSDD is described in details in Section 3.Considering the practicability,the detection performance of the DF-S-MSDD is discussed by simulations in Section 4.Finally,conclusion is shown in Section 5.
Notations:lower-case (upper-case) boldface symbols represent vectors (matrices);()Tand Tr() denote the transpose and the trace of a matrix,respectively;* stands for convolution;δ(t) represents the Dirac delta function.
1 System description
In this section,the multiple-input multiple output (MIMO) system description will be introduced for point-to-point UWB system with DSTBC modulation.The transmitter is equipped withT(T>1) transmit antennas,the receiver is equipped withR(R>1) receive antennas.At the transmitter,Sdenotes the date rate,TSbits map toT×Tunitary matricesCi,which is thei-th information symbol.With the aid of differential encoding,the transmission symbol is given as
Gi+1=GiCi+1
(1)

(2)
where,tis time parameter,ω(t) represents the monocycle pulse with durationTω,Tfis the frame duration,the duration for transmitting a symbol isTs=2Tf,which indicates that 2 frames are needed to transmit one information symbol,Ebis the energy for transmitting one bit.To facilitate the demonstration,j=2i+n-1 is brought,andgm,2i+n-1is simplified asgm,jcorrespondingly.Then
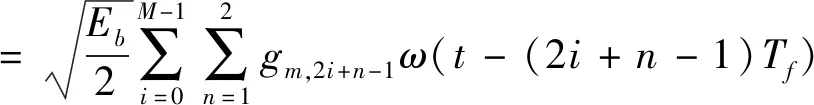
(3)
The channel impulse response between them-th transmit antenna and ther-th (1≤r≤R) receive antenna is given by
(4)
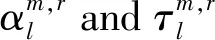
(5)
As a result,the received signal at ther-th receive antenna can be expressed as
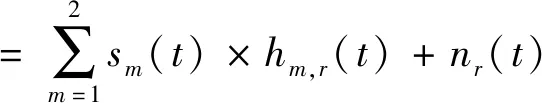
(6)
wherenr(t) is the additive white Gaussian noise (AWGN),its mean is zero and power spectral density isN0/2 with two-sided.To help understand and implement the proposed algorithms,the received signal fromRreceive antenna can be rewritten with matrix as
(7)
The noncoherent transmission is designed under the the assumption,that the channel is constant duringTsymbols intervals[12].Based on the assumption and the received signal in Eq.(7),MSDDs will be formulated in the UWB system with DSTBC modulation.
2 GLRT-MSDD and DF-MSDD
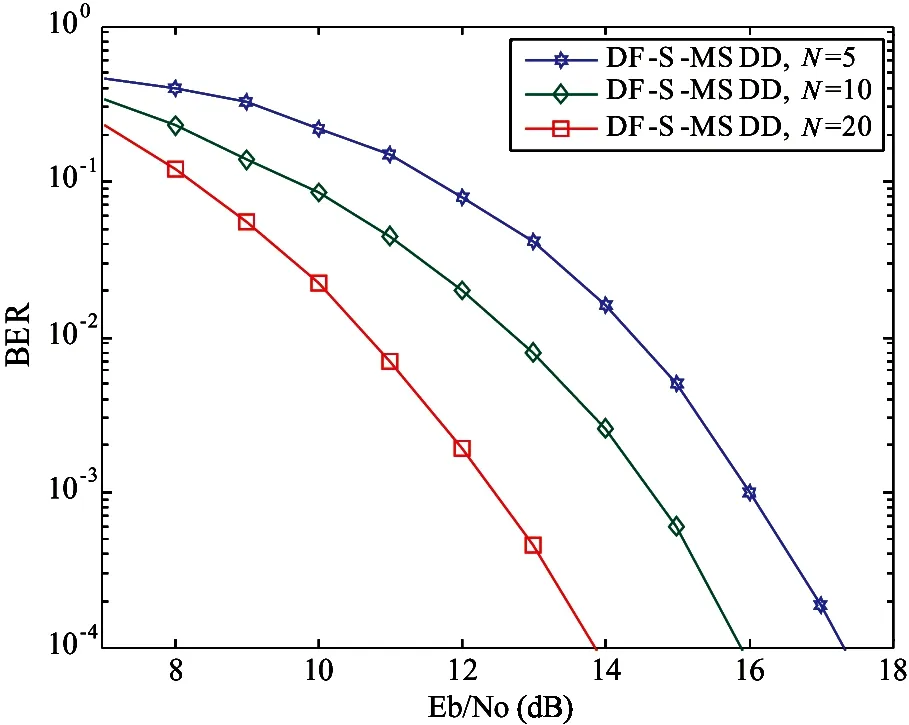
It is assumed that the number of the observation window isNDSTBC symbols.The target is how to detectN-1 information-bearing symbols jointly from theNreceived symbols.As such,the relationship is investigated between the information symbolsCiand the received symbols.Firstly,N-1 information symbols are expressed as the setC=[C1,C2,…,CN-1].Furthermore,Cwill be detected from the received signal {yr(t)} ofNobservation window,where 0 (8) whereQβ,γis the correlation matrix received fromRreceive antenna,its entries are the correlation function of theβ-th and theγ-th received signal expressed as (9) (10) According to the DF-MSDD given in Eq.(10),it is obvious that only a codeword symbol is detected in a observation window.Thus,when compared to the GLRT-MSDD,the computational complexity of DF-MSDD will be reduced significantly.On the other hand,it is pointed out that[19],the reliability of the estimated symbols in the middle of the observation window is higher than that at the edge.Thus,for the DF-MSDD,the error detection on the edge of the observation window results in performance loss.Therefore,DF-MSDD is modified,and DF-S-MSDD is proposed in the next section. In the GLRT-MSDD,N-1 information symbols can be estimated from the observation ofNsymbols;for the DF-MSDD,the previousN-2 estimated symbols are feedback,and then the last symbol is detected.In the following,the DF-S-MSDD will be formulated.For the DF-S-MSDD,the previouN-2-ιsymbols are feedback,and the optimization is employed over the lastι+1 symbols with GLRT-MSDD.Moreover,in order to reduce the performance loss caused by the inaccuracy at the edge of the observation,instead of returning all theι+1 decision symbols but onlyι+1-ζsymbols,and the remainingζdetection symbols are discarded at the edge of the observation.Accordingly,the sampling architecture for the DF-S-MSDD is designed.Note that the observation window slides forwardι+1-ζsymbol durations each time.The proposed sliding mechanism is particularly suitable for extracting the cross-correlation information among different blocks. In this section,Monte-Carlo simulations are carried out to validate the advantages of the proposed noncoherent transmission in the UWB system with DSTBC.The channel is given as the IEEE 802.15.3a CM2 model[16].The monocycle waveformω(t) isω(t)=[1-4π(t/Tω)2]exp[-2π(t/Tω)2],where the pulse duration isTω=0.287 ns.The frame duration isTf=80 ns,the maximum excess delay of the channel is chosen asTn=40 ns,whereTf>Tneliminates the inter-symbol interference.The transmit antenna is set toT=2.Furthermore,when the receive antenna isR=1,ι=1,ζ=1,the BER performance of the DF-S-MSDD is demonstrated.Specifically,as shown in Fig.1,as the observation window increases from 5 to 10 and 20,the BER performance of the proposed DF-S-MSDD has been improving.When the size of observation window isM=10,the SNR is 9-10,as shown in Fig.2,the BER performance of the DF-MSDD is less than DF-S-MSDD about 0.3 dB.This is due to the accurate detection at the edge of the observation window for the DF-S-MSDD. In contrast to the existing DF-MSDD in UWB system with DSTBC,the proposed DF-S-MSDD generates the performance gain by discarding the symbols at the edge of the observation window.On the other hand,DF-S-MSDD requires a low computational complexity by exploiting the decision-feedback.Finally,Monte-Carlo simulations confirm that DF-S-MSDD provides the BER performance better than the DF-MSDD benchmarker regardless of the number of the observation window,whereas with a reasonable complexity. Fig.1 BER performance of the proposed DF-S-MSDD in the UWB system with DSTBC Fig.2 BER performance comparison of the proposed DF-S-MSDD and DF-MSDD in the UWB system
3 DF-S-MSDD in UWB system
4 Simulations and analysis
5 Conclusion

杂志排行
High Technology Letters的其它文章
- A bibliometric analysis of gene editing research①
- A hybrid optimization approach for the heterogeneous vehicle routing problem with multiple depots cooperative operation①
- Airport gate assignment problem with deep reinforcement learning①
- Research on transient characteristics of cavitation phenomena in pilot stage of jet pipe servo-valve①
- A 16-channel high-voltage reconfigurable and flexible-controlled implantable wireless closed-loop system for SCI repair①
- Optimization of yield criterion and simulation based on QP980 high strength steel①
