Improved Fx-VSSLMS algorithm for active vibration control of smart cantilever beam①
2020-04-10FangYubin方昱斌ZhuXiaojinLiXiangminMiaoZhonghuaGaoZhiyuanZhangHesheng
Fang Yubin(方昱斌),Zhu Xiaojin,Li Xiangmin,Miao Zhonghua,Gao Zhiyuan,Zhang Hesheng
(School of Mechatronic Engineering and Automation,Shanghai University,Shanghai 200072,P.R.China)
Abstract
Key words:active vibration control (AVC),filtered-x least mean square (Fx-LMS),variable step size least mean square (VSSLMS),robustness,flexible beam
0 Introduction
In the field of mechanical engineering,the increasing flexible structures are applied for lightweight and system stability[1].But it may introduce vibration when working with uncertain load and external disturbance.However,mechanical flexible structures often incur unwanted vibration which can significantly degrade the performance and even result in catastrophic system failure[2].Thus,to suppress the vibration of flexible structure effectively is a significant issue[2].A lot of achievements have been obtained in theoretical and practical researches on the active vibration control(AVC) of flexible structure[3-6].While focusing on the control method,the adaptive control has obtained wide attention for its good adaptability to time-varying system.
Filtered-x least mean square (Fx-LMS) is one of the most popular adaptive algorithms in active vibration control applications due to its robustness and easiness to use.The block diagram illustrating Fx-LMS algorithm in feedforward AVC system was presented[8].
Although Fx-LMS algorithm has many advantages in adaptive application,there are also some defects in the tradeoff of convergence speed and steady-state error caused by fixed step size of LMS algorithm.Specifically,large step size can get quick convergence,also get large mean square error (MSE) in steady-state.On the other hand,small step size makes the convergence slow.Therefore,many kinds of VSSLMS algorithms were proposed[9].
Most of the VSSLMS algorithms were proposed in applications of system identification.In AVC systems,the step size may change to a big value when a sudden disturbance occurs.Thus,the system may oscillate near the steady-state,even be divergent.Therefore,the robust to noise disturbance of VSSLMS algorithm should be considered when they are used in AVC system.
In this work,nine VSSLMS algorithms are reviewed in detail and an improved VSSLMS algorithm is developed to get better robustness performance.An AVC experimental system of flexible piezoelectric cantilever beam is set up to compare the performance of these VSSLMS algorithms.The above 10 VSSLMS algorithms are used in the feedforward filtered-x structure and compared in AVC experimental system in different noise level.The experiment results prove the robust to noise of the developed VSSLMS algorithm.
The rest of the paper is organized as follows.Section 1 reviews nine VSSLMS algorithms in detail.Section 2 proposes an improved VSSLMS algorithm.Complexity comparison of these VSSLMS algorithms is given in Section 3.An AVC experimental system of flexible piezoelectric cantilever beam is set up in Section 4.And the performance of these VSSLMS algorithms are compared and analyzed.Some conclusions are drawn in Section 5.
1 VSSLMS algorithms
The block diagram of Fx-LMS algorithm in AVC was shown in Fig.1.The residual errore(n) is obtained through vibration response of disturbance and control output.It can be expressed as
e(n)=d(n)-S(n)×[WT(n)x(n)]
(1)
where,nis the time index,S(n) is the impulse response of the secondary pathS(z) which includes the digital-to-analog converter,reconstruction filter,power amplifier,vibrational path from actuator to error sensor,error sensor,and analog-to-digital converter and so on.The coefficients of adaptive filterWis adjusted to minimize the square of residual error through LMS algorithm.The adaptive filter has the finite impulse response (FIR) type:
W(n)=[w0(n)w1(n) …wL-1(n)]T
(2)
And LMS algorithm updated the filter coefficients according to the well-known formula[8]:
W(n+1)=W(n)+μx′(n)e(n)
(3)


Fig.1 Block diagram of Fx-LMS algorithm in feedforward AVC system
As the important part of Fx-LMS algorithm,LMS algorithm has some weaknesses about its fixedstepsize.For improving the effect of this algorithm,nine typical VSSLMS algorithms were presented.These VSSLMS algorithms are classified into 4 series by the characteristicof their step size updating formulas.All symbols used in this section have been listed in Table 1.
1.1 VSSLMS-A1
Shan et al.[10]proposed a VSSLMS algorithm in 1988 and simplified the original version in 1990.The simplified edition is currently known as correlation LMS algorithm,which is given as

Table 1 List of symbols
(4)
ρ(n+1)=λρ(n)+(1-λ)x(n)e(n)
(5)
where,μ(n) satisfies 0<μ(n)<μmax[11],ρ(n) is an estimate of the correlation between input signal and error signal at timen.And the authors suggested that the scaling factorαshould be chosen experimentally,the forgetting factorλgot the value in the range of [0.9,1].The authors claimed their algorithm was robust in the disturbance and the case of sudden changes of noise level.
1.2 VSSLMS-A2
Ramadan et al.[12]proposed this VSSLMS algorithm in 2005 which is given as
(6)
(7)
where,‖e(n)‖2is the square norm of the error vector,‖eT(n)‖2is the square norm of the error vector withTlength.
The authors claimed that their algorithm showed better performance in the stationary environments and especially in responding to an abrupt change in the unknown system parameters.
1.3 VSSLMS-B1
Karni et al.[13]proposed VSSLMS algorithm in 1989 which is given as
μ(n)=μmax(1-exp(-ν‖x(n)e(n)‖2))
(8)
where,μ(n) satisfies 0<μ(n)<μmax.
Ref.[13] suggested dumping factorνcould get a value larger than 1.Ifν→∞,the algorithm become the conventional LMS algorithm andμ=μmax.Ref.[13] compared their algorithm with the 2-stage method and got a faster convergence speed and a smaller misadjustment.
1.4 VSSLMS-B2
Li et al.[14]proposed VSSLMS algorithm in 2009.The step size is updated as
(9)
μ′(n)=λμ′(n-1)+(1-λ)|e(n-1)e(n)|
(10)
(11)
The hop dumping factorν(n) is initial asν1at the beginning of adaptation.When the ratio ofν(n)/ν(n-1) is larger than a thresholdτ,the hop dumping factorν(n) is jumped toν2.
1.5 VSSLMS-C1
Benveniste et al.[15]proposed VSSLMS algorithm in 1990.The algorithm was cited by many papers,such as Refs[16,17].Based on Ref.[9],the algorithm is given as
μ(n)=μ(n-1)+γe(n)xT(n)φ(n)
(12)
whereμ(n)<μmaxshould be satisfied.
φ(n+1)=φ(n)-μ(n)x(n)xT(n)φ(n)
+x(n)e(n)
(13)
where,γis a small positive value to control the convergence speed and MSE,andφ(n) is an estimate of the gradient vector.
1.6 VSSLMS-C2
Mathews et al.[18]proposed VSSLMS algorithm in 1993 which can use both individual and scalar step sizes.For the scalar step size case,it is given as:
μ(n)=μ(n-1)
+γe(n)e(n-1)xT(n-1)x(n)
(14)
Andμ(n) should have the upper and lower limitsμmin<μ(n)<μmax.In this case,0<μ(0) should be satisfied.
Ref.[18] claimed that the value ofγwas not critical to choose.At the same time,considered their algorithm could offer ‘close to the best possible performance’ in the nonstationary conditions.
1.7 VSSLMS-D1
Kwong et al.[19]proposed the following algorithm in 1992:
μ(n)=ξμ(n-1)+ηe2(n-1)
(15)
Ref.[19] claimed that the value ofξshould be between 0 and 1,and 0.97 was the optimum in their many simulations.ηinfluences both the convergence speed and MSE,it should be small.Also,the algorithm has the upper limitμmaxand lower limitμmin.
The step size of the algorithm is correlated with the square of the error.Then the algorithm can have fast adaptation when the error is large.VSSLMS algorithm also reduces sensitivity of the misadjustment to the level of nonstationary.A significant feature of the algorithm is that approximate formulas can be derived to predict the misadjustment in both stationary and nonstationary environments.These theoretical predictions agree well with simulations of the algorithm.Ref.[19] claimed that their algorithm performs at least as well as when compared to the Harris’[20]algorithm.
1.8 VSSLMS-D2
Aboulnasr et al.[21]modified the Kwong’s[19]algorithm in 1995 in order to solve the problem that Kwong’s[19]algorithm may be unstable in the instantaneous energy of the error signal.Aboulnasr et al.[21]used the estimate of the autocorrelation betweene(n) ande(n-1) to control the step size instead ofe2(n).The algorithm is given as
μ(n)=ξμ(n-1)+ηp2(n-1)
(16)
p(n)=λp(n-1)+(1-λ)e(n)e(n-1)
(17)
whereλis in the range of [0,1] and close to 1.
ξandηcan take the same value as the Kwong’s[19]algorithm.Also,the same upper and lower limits can be applied.Ref.[21] claimed that their algorithm got better performance in the stationary environments and a comparable performance in the nonstationary environments.But on the other hand,this algorithm has 3 parameters to be adjusted.
1.9 VSSLMS-D3
Huang et al.[22]proposed VSSLMS algorithm in 2015.The step size is updated as
μ(n)=ξμ(n-1)+ηe2(n-1)e2(n-2)
(18)
Ref.[22] claimed that the algorithm had a comparable convergence ability and MSE with other VSSLMS algorithms.The obvious advantages are high computational efficiency and tracking capabilities in both stationary and nonstationary environments.
2 The proposed VSSLMS algorithm and performance analysis
The step size of VSSLMS-D1[19]is correlated with the square of instant error.The amplitude of instantaneous error is oscillating.Besides,it is usually mixed with measurement noise.Thus,it is sensitive to the noise disturbance.Based on the insight gained from the above VSSLMS algorithms,an improved one was developed.The idea is to make parameterηin VSSLMS-D1 varying with the time for better performance.The proposed algorithm is updated as follows:
μ(n)=ξμ(n-1)+η(n)e2(n)
(19)
η(n)=α×arccot(|e(n)|)
(20)
(21)
In the proposed VSSLMS algorithm,parameterη(n) is related to the sequence ofe(n),and parameterαis used to adjust the scale of parameterη(n).This algorithm can restrain influence of abrupt input signal.It has better robustness compared to VSSLMS-D1 in steady-state.The performance analysis of the proposed algorithm will be a topic of future research.In this work,abundant experiments with AVC system are conducted to verify the effectiveness of the new algorithm.
3 Comparison of complexity
For the algorithms mentioned above,majority of them need upper limit to run.And some of them need both upper and lower limits.In fact,the only algorithms that do not require upper limit are VSSLMS-B2[14]and VSSLMS-D3[22].
The upper limit should guarantee convergence as well as not impose too much restrictions on the step size[9].However,lower limit can be chosen very roughly.Thus,the upper and lower limits could not be counted as the number of parameters to be adjusted.There is a small constantεin VSSLMS-A2[12]to prevent instability.It can be chosen as a small value roughly as the lower limit.Also,the constantεcould not be considered as a parameter that should be adjusted.
The comparison of complexity between the above mentioned VSSLMS algorithms is made through 4 indicators:the number of parameters,the number of additions,multiplications and divisions respectively in each iteration.The results of comparison are shown in Table 2.
VSSLMS-B1,VSSLMS-C1 and VSSLMS-C2 only need to adjust 1 parameter.This makes them more convenient in practical application.The algorithms needing more than 3 parameters to adjust are VSSLMS-A2,VSSLMS-B2 and VSSLMS-D2.It is an obvious disadvantage.

Table 2 Comparison of complexity between the above mentioned VSSLSM algorithms
VSSLMS-D1 needs a minor computation cost:one addition and 3 multiplications in each iteration.Also,VSSLMS-D3 and VSSLMS-New have a competitive computation.Conversely,the algorithms needing relatively high computation cost are VSSLMS-A2,VSSLMS-B1,VSSLMS-C1 and VSSLMS-C2.It may influence the real-time performance.
The proposed VSSLMS-New has 2 parameters to be adjusted before running.There are only 1 addition and 4 multiplications in each interaction.It is competitive both in number of parameters and computation in the above VSSLMS algorithms.
4 VSSLMS algorithm in active vibration control
4.1 Experimental setup
In this work,an AVC experimental system of flexible piezoelectric cantilever beam is established.To illustrate the functionality of each components,a schematic of the experimental setup is presented in Fig.2.There are 6 piezoelectric patches on the cantilever beam.Two of them are used as sensors to measure the vibration.The one nearing cantilevered base is named as reference sensor,and the one near free end is named as error sensor.The other four are used as actuators.To strengthen the output of the actuators,every 2 piezoelectric patches are bonded on both sides of the beam at the same location.The group closer to the cantilevered base is named as the disturbance actuator.Another group is named as the suppression actuator.In this work,the control objective is to suppress the vibration of the flexible piezoelectric cantilever beam gathered by error sensor.For the sketch of flexible cantilever beam in Fig.2,parts of parameters are given in Table 3.
By using the real-time workshop toolbox in Simulink,two industrial computers (ACP-4020,AdvantechⒸ) are combined as target PC and host PC respectively.A DAQ card (PCI-6289,NIⒸ) is used for data collection and implementation of control algorithms.The control signal with 0-10 V is amplified to 0-300 V by the piezoelectric power amplifier (E00.A4,XMTⒸ).And the piezoelectric actuator is used to suppress the vibration.The sensor signals are amplified by the charge-amplifier (YE5852A,SINOCERAⒸ).The picture of experimental system is shown in Fig.3.
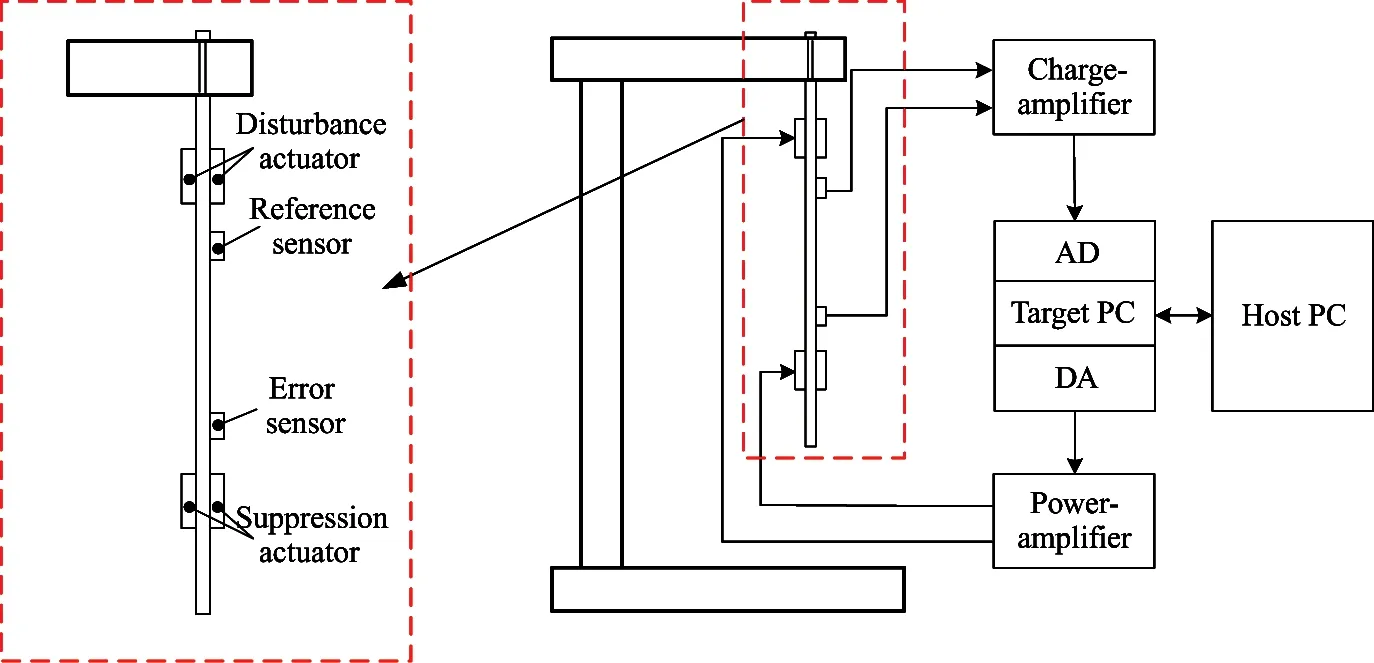
Fig.2 Block diagram of cantilever beam experimental system

Fig.3 Picture of AVC experimental system

Table 3 Parameters of the cantilever beam
4.2 Experimental results
Here,VSSLMS algorithms are implemented in the feed forward filtered-x adaptive AVC system.As the energy of the vibration is concentrated in first few orders resonance frequency,a sine signal with the known resonant frequency 20.53 Hz is used as the disturbance to excite vibration of the beam.Also,wideband noise with different variances of 0.001 and 0.0001 is combined respectively to compare the robustness of VSSLMS algorithms.All user parameters are adjusted very carefully to let the VSSLMS algorithms have a fairly competition.Moreover,the choice of these parameters is also guided by the recommended values in their work.The step sizes of all VSSLMS algorithms have the same upper and lower limits if they need.The initial step size of all the VSSLMS algorithms are the same value,such that all these algorithms present similar initial convergence speed.
Performance comparison is made in terms of total MSE.First,all these VSSLMS algorithms are adjusted to a same MSE (-40 dB) in steady-state without noise disturbance.Then,the disturbance signal with different level noise are implemented to reveal the robustness to noise of these VSSLMS algorithms.The MSE can be achieved from Eq.(22).
MSE(n)=E(e2(n))
(22)
It can manifest the overall performance of the algorithms,including the convergence speed and the stead-state error.With averaging 200 individual runs,the results of simulations are shown in Fig.4,Fig.5 and Fig.6.Fig.6 presents the MSE curves of VSSLMS algorithms without noise disturbance.Fig.6 and Fig.7 present the MSE curves of VSSLMS algorithms with different noise levels respectively.
Figs 4(a)-(d) show the vibration suppression performance of series A,B,C and D VSSLMS algorithms respectively.VSSLMS-A1 has a slightly faster convergence speed than VSSLMS-A2.VSSLMS-B1 is noticeably faster than VSSLMS-B2.VSSLMS-B1 has the fastest convergence in all these VSSLMS algorithms.It reaches stead-state in control time of 80 s.VSSLMS-C2 gets a little faster convergence speed than VSSLMS-C1.In series D VSSLMS algorithms,the 3 algorithms have an almost unanimous convergence speed although VSSLMS-D2 has a little advantage.
As the same,Figs 5(a)-(d) and Figs 6(a)-(d) show the vibration suppression performance of series A,B,C and D VSSLMS algorithms respectively in lower and higher noise level.All the VSSLMS algorithms obtain a worse MSE more or less,especially in higher noise level.As the fastest algorithm in Fig.4,VSSLMS-B1 gets the worst MSE in noise disturbance environment.It only reaches 38 dB in the higher noise level.Also,in Fig.7,the series C and D get a clearly worse MSE than them in Fig.4.It is not obviously different in the suppression performance of series D VSSLMS-D in the noise environments.VSSLMS-D2 has some disadvantages in convergence speed than VSSLMS-D1 and VSSLMS-D3 in higher noise level.
To compare the performance of VSSLMS-New,the fastest convergence algorithms are chosen from every series.They are VSSLMS-A1,VSSLMS-B1,VSSLMS-C2 and VSSLMS-D2.The vibration suppression performance of VSSLMS-New compared with the above 4 algorithms are shown in Fig.7.Fig.7(a),Fig.7(b) and Fig.7(c) are the MSE cureves respectively in zero noise,lower noise and higher noise environment.
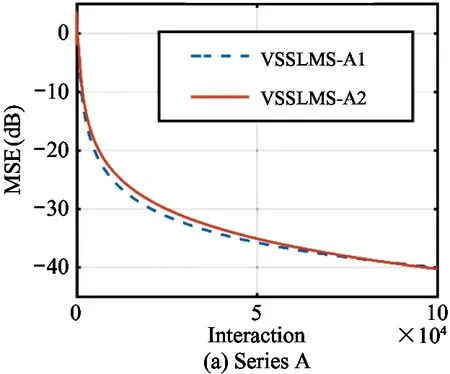



Fig.4Comparison of MSE curves of VSSLMS algorithms without nosie
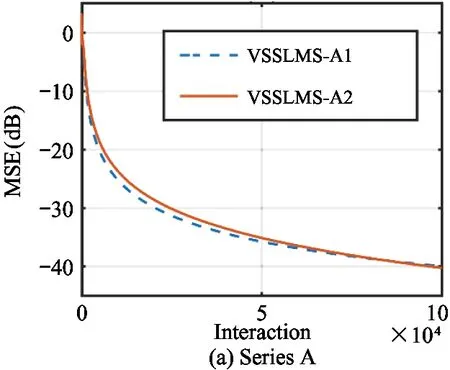



Fig.5Comparison of MSE curves of VSSLMS algorithms with lower noise level (σ2=0.0001)

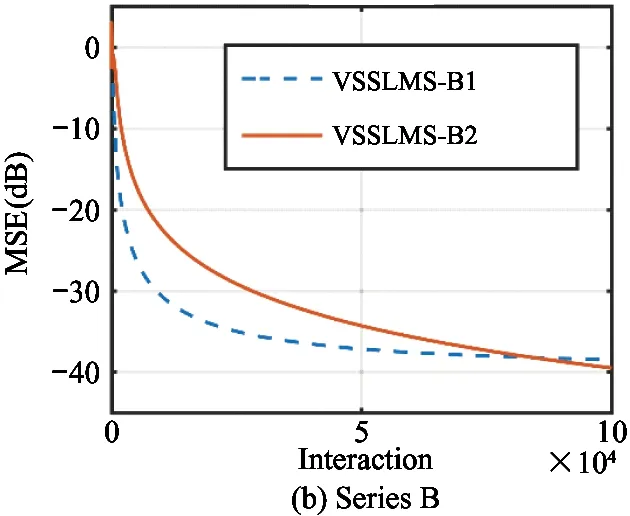


Fig.6Comparison of MSE curves of VSSLMS algorithms with higher noise level (σ2=0.001)
In Fig.7(a),VSSLMS-B1 presents the advantage in convergence speed than the other algorithms.VSSLMS-New gets the medium level in these algorithms.It is better than VSSLMS-C1 and VSSLMS-A1.When in the noise environments as Fig.7(b) and Fig.7(c) shown,VSSLMS-New presents lower MSE in stead-state than others.It shows that VSSLM-New has a better robustness to noise.It is gratifying that VSSLMS-New obtains a better grade in convergence speed in higher noise level.VSSLMS-D2 does not converge fast as it in Fig.6(a).There is only VSSLMS-B1 converging faster than VSSLMS-New.Unfortunately,the stead-state performance is not good.



Fig.7Comparison of VSSLMS-New and the fastest VSSLMS algorithms of series A,B,C and D for different noise level
5 Conclusion
Nine VSSLMS algorithms are reviewed and the computational complexity of these VSSLMS algorithms are compared.A new VSSLMS algorithm is proposed for AVC of the smart cantilever flexible beam.The new algorithm adopted a time-varying parameter based on instantaneous error to improve the robust performance to noise disturbance.As a result,the proposed algorithm can effectively isolate the influence of noise on step size.By an AVC experimental system of the flexible piezoelectric cantilever beam,the performance of the proposed algorithm is compared with other VSSLMS algorithms.Results show that the proposed algorithm has better robustness to noise both in high and low noise levels compared with other VSSLMS algorithms.
杂志排行
High Technology Letters的其它文章
- A bibliometric analysis of gene editing research①
- A hybrid optimization approach for the heterogeneous vehicle routing problem with multiple depots cooperative operation①
- Airport gate assignment problem with deep reinforcement learning①
- Research on transient characteristics of cavitation phenomena in pilot stage of jet pipe servo-valve①
- A 16-channel high-voltage reconfigurable and flexible-controlled implantable wireless closed-loop system for SCI repair①
- Optimization of yield criterion and simulation based on QP980 high strength steel①
