基于云平台下的并行VMD算法

贾亚飞， 兰志堃， 王凌霄， 李国超， 朱永利

(1.河北省电力有限公司雄安新区供电公司，河北 雄安新区 071800； 2.河北省电力有限公司保定供电公司，河北 保定 071000； 3.华北电力大学 控制与计算机工程学院，河北 保定 071003)

0 引 言

2019年1月，国家电网公司正式提出建设枢纽型、平台型、共享型企业，在坚强智能电网基础上建设泛在电力物联网，共同构成能源流、业务流、数据流“三流合一”的能源互联网，这是适应内外部形势和挑战的必然要求[1]。泛在电力物联网将电力用户、电网企业、发电企业、供应商及相关设备，连接起来，产生共享数据，物联网是能源互联网的基础。

随着智能电网建设的不断推进，智能化电力一次设备和常规电力设备的在线监测都得到了较大发展并成为趋势，在线监测数据日益庞大[2，3]。另一方面，在电力行业发展的过程中已经积累了大量的、有价值的电力设备状态历史数据。这些数据对分析电力设备运行状态和电网管理决策提供了数据支持，同时这些数据也是泛在电力物联网的重要组成部分[2]。面对电力系统海量监测数据、信息与物理系统间的复杂交互作用，传统的分析技术难以满足智能电网的安全分析与稳定控制需求。如何有效分析处理这些海量电力设备的监测数据是一个重要的研究方向。

大数据技术是一种可以处理海量数据的新的数据处理模式。所谓的大数据带给我们的三个颠覆性观念转变：是全部数据，而不是随机采样；是大体方向，而不是精确制导；是相关关系，而不是因果关系。大数据技术的战略意义不在于掌握庞大的数据信息，而在于对这些含有意义的数据进行专业化处理。电力大数据是能源变革中电力工业技术革新的必然过程，也是泛在电力物联网强有力的支撑。

Apache Storm和Apache Spark云平台都是Apache旗下的顶级项目之一，都能为广大用户提供良好的实时内存处理环境[4]。其中，Storm是一套专门用于流数据处理的分布式计算框架，极具可扩展能力和快速容错能力。Storm在事件处理与增量计算方面表现突出，能够以实时方式根据不断变化的参数对数据流进行处理。Spark也专门面向实时分布式计算任务，较Storm而言，Spark是一套更具泛用性的分布式计算平台，支持SQL查询、流式计算、图计算、机器学习等多种计算范式。它提供了包括map(映射)和reduce(归约)在内的80多种算子，计算模型较Hadoop的单一MapReduce模型更为丰富和灵活，且能够兼容HDFS、HBase、Hive等多种数据源。与Hadoop中需要频繁的磁盘I/O不同，Storm和Spark均尽量采用内存计算[3]，极大地提高了大数据处理速度，满足了实时场景的需求。Storm主要面向实时产生、高并发的数据流，数据以元组为单位在事先设计且链接好的管道式的组件中流过并被分析，处理延迟较低，能够小于1 s。而Spark将已存储的大量离线数据批量加载进内存后再进行并行处理，整体完成时间在数秒以上到1 min。两种计算平台的设计模式各有特点，适用场景也有所差异，因此配合使用能相得益彰。正因为Storm和Spark具有诸多优势，本文采用这两个云平台对电力设备的监测数据进行处理。

在电网众多的电力设备监测数据中，时序波形信号数据的占有量较大，是评估电力设备状态的重要依据。然而，时序波形信号难以将其直接用于设备的状态诊断，必须经过信号处理和特征量提取。已应用于电力设备监测数据分析的方法包括：FFT(fast Fourier transform)、小波变换和总体经验模态分解(EEMD)方法等。 FFT 适合处理平稳信号[5，6]，而电气设备很多在线监测信号(如绝缘放电电流或超高频信号)属于非平稳信号。虽然小波变换适合分析非平稳信号，但在选择小波基和分解层数时存在一定的难度，无法实现信号的自适应分解[7]，且由于基函数的长度有限，在对信号进行处理时会产生能量泄漏。总体经验模态分解(EEMD)方法以经验模态分解(EMD)方法为内核，解决了由间歇性成分(间断噪声)导致的模态混叠问题，但并未解决由脉冲噪声引起的模态混叠问题[7，8]。因此，寻找更加有效的分析算法具有重要的现实意义。

变分模态分解(Variational Mode Decomposition，VMD)是一种完全非递归的变分模态分解方法[8，9]。VMD的整体框架是变分问题，通过交替方向乘子法(Alternate Direction Method of Multipliers，ADMM)迭代搜索变分模型最优解，使每个模态的估计带宽之和最小，且每个模态是具有不同中心频率的有限带宽[10-13]。VMD具有坚实的理论基础，有效解决了EMD，EEMD等递归式分解方法存在的模态混叠和相近频率分量无法正确分离的问题[14]。VMD本质是多个自适应维纳滤波组，具有较好的噪声鲁棒性[9]。正是由于该方法的诸多优点，近年来得到广大学者的关注。

为实现VMD算法在云平台上的应用，首先必须对VMD算法在云平台上实现的可行性进行论证。该技术实现过程中，信号分段边界的处理和各段分析结果的合成是关键。为解决上述问题，本文提出一种基于矩形窗分段的VMD分析方法(the VMD algorithm based on rectangular window segmentation，VMD-RWS)对数据量较大的局部放电信号进行分析，并提出一种基于信号局部平稳度的自适应分段和外推延拓(the adaptive subsection based on local flatness and extrapolation，ASLF-E)的边界补偿方法，以保证各子段的模态分量在窗口截断处连续。实验结果证明该方法适合在云平台上实现信号的分段处理和合成，论证了VMD算法在云平台上实现的可行性，为云平台下VMD算法的应用提供了一种切实可行的方案。此外，本文设计了电力设备监测信号应用并行VMD算法分别在Storm和Spark平台上处理的流程及架构，为基于云平台的并行VMD算法的实现提供了依据。

1 VMD算法

VMD算法是一种完全非递归、准正交、自适应的新的分解方法，其目标是将由多分量组成的信号f分解成若干个有限带宽的模态分量uk，每个模态的绝大部分都紧紧围绕在中心频率ωk周围。

VMD算法实质就是变分问题的求解，主要包括变分问题的构造和求解两部分。各模态直接在频域不断更新，最后通过Fourier逆变换变换到时域。作为各模态的功率重心，中心频率被重新预估，并以此循环更新。VMD算法的具体步骤可参见文献[9，11]，本文仅做简要介绍。

假设将原始信号f分解为K个模态分量uk(t)(k=1, 2, …,K)，每个模态的估计带宽之和最小，约束条件为各模态之和等于输入信号f，则变分约束问题如下：

(1)

式中：{uk}:={u1,…,uK}为分解得到的K个模态分量；{ωk}:={ω1,…,ωK}为各模态分量的中心频率。

为求解上述约束变分问题，将约束性变分问题变为非约束性变分问题，引入二次惩罚因子α和拉格朗日惩罚算子λ(t)，构成扩展的拉格朗日函数，如式(2)所示：

(2)

式中：α为二次惩罚因子；λ(t) 为拉格朗日算子。

(3)

利用 Parseval/Plancherel 傅里叶等距变换将式(3)变换到频域，并求解该二次优化问题的解，如式(4)所示：

(4)

同理得到中心频率的更新方法，如式(5)所示：

(5)

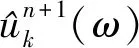
2 并行 VMD 算法

电力设备的运行状态需要进行长时间的监测，因此得到的监测数据的数据量很大。对于较长的波形信号，直接进行处理很困难，可以将其分割成多个子波形段(Epoch)，然后对各Epoch进行VMD后再将结果进行合并，这些子段的VMD过程是可并行的。因此，VMD算法存在 Epoch 级并行。

由于VMD算法本身存在边界效应，且不同截断点对重构精度也存在影响，因此，在VMD算法进行Epoch 级并行时，原信号分段后分别进行VMD再将结果合并必将在分段处产生误差。为了解决以上问题，本文提出一种基于信号局部平稳度的自适应分段和外推延拓(the adaptive subsection based on local flatness and extrapolation，ASLF-E)的边界补偿方法，以保证各子段的模态分量在窗口截断处连续。

2.1 VMD算法的边界效应

由于VMD算法实现过程需要Fourier变换及其反变换，若被分析信号两端不进行处理直接进行VMD分解，可能会在边界处产生较大的误差，即VMD算法的边界效应。

可采用对信号两端进行延拓的方法来抑制VMD算法的边界效应。常用的延拓方法有补零延拓，周期延拓和镜像延拓等。其中补零延拓操作简单，但处理效果较差。周期延拓通常会在边界处人为地产生一个信号阶跃，不能保证延拓信号在边界处的连续性，致使数据段边界处的时频信息误差较大[15]。镜像延拓可以保证时域信号在边界处的连续性[16]。因此，本文采用镜像延拓对原信号两端进行补偿，以限制原信号两端的边界效应。

有限长度的放电可以看作是无限长信号被矩形窗截断所得。图1为某仿真信号直接采用VMD算法进行分解和对信号两端进行镜像延拓后采用VMD算法进行分解得到的模态分量在边界处的放大图。由图1可知，信号两端经镜像延拓后进行VMD分解得到的模态分量边界处与信号原始分量基本吻合，而直接进行VMD分解得到的模态分量边界处出现较大误差，说明对信号两端进行镜像延拓可以有效抑制VMD算法的边界效应。

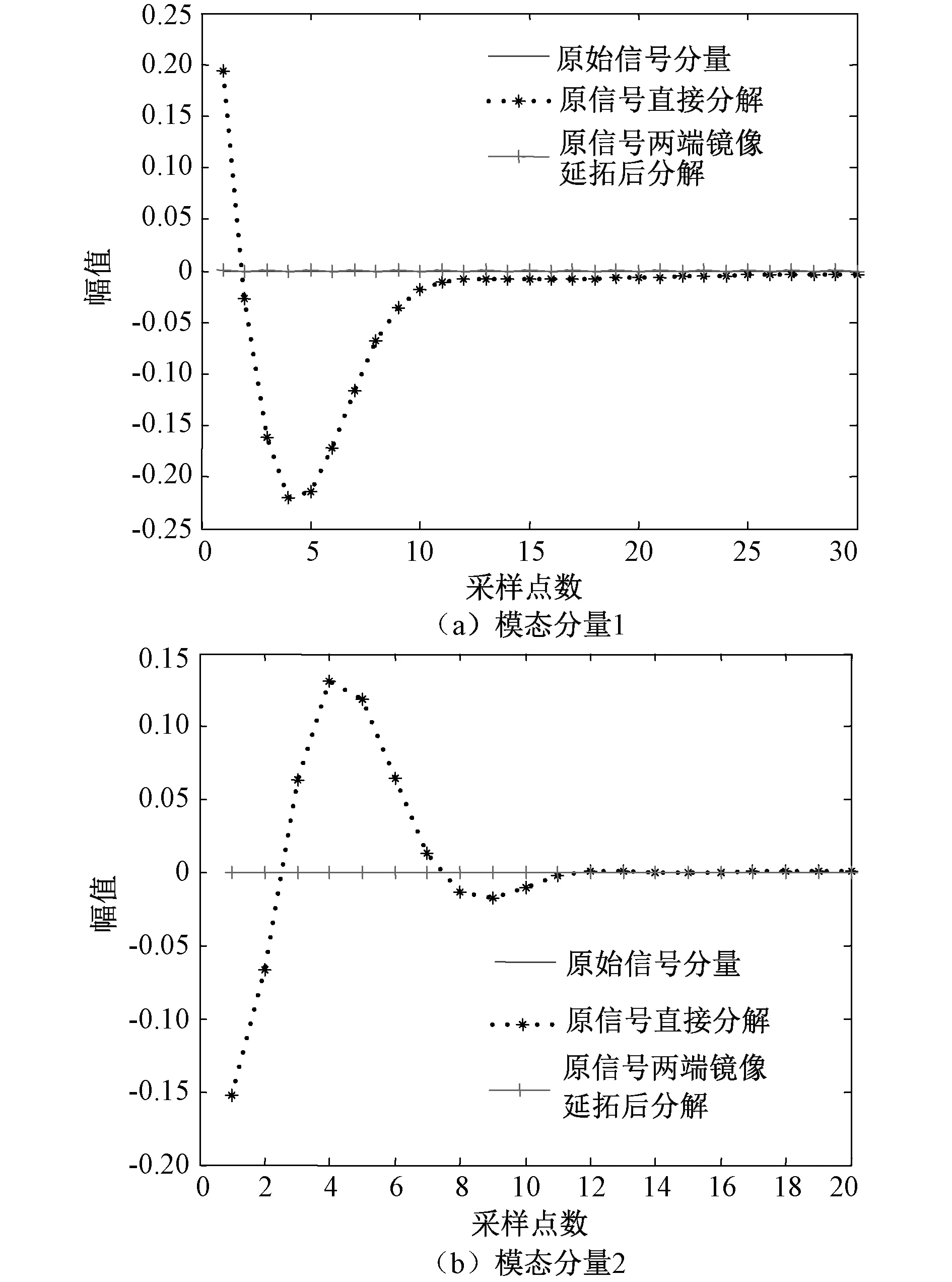
图1 VMD算法的边界效应Fig.1 Boundary effect of VMD algorithm

2.2 不同矩形窗截断点对子段VMD分解模态重构精度的影响

本文采用矩形窗函数将原始信号截断成若干个子段数据。矩形窗属于时间变量的零次幂窗，其数学表达式为

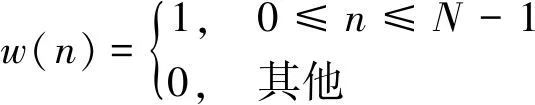
(6)

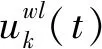
(7)

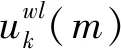
为了说明VMD算法在窗口截断处的边界效应以及不同截断点对模态分量重构精度的影响，本文进行了简单的仿真实验。构造单指数和双指数衰减振荡函数来模拟在监测数据中常见的局部放电信号，数学表达式分别为

s1(t)=A1e-(t-t〗-0)/τsin(2πf1t)

(8)

s2(t)=A2[e-1.3(t-t0)/t-e-2.2(t-t0)/t]sin[2πf2(t-t0)]

(9)

因为放电信号通常具有较高的频率，为了模拟放电信号特征，采样频率为fs=1 GHz；单指数衰减振荡函数s1的幅值为A1=80，频率为f1=150 MHz；双指数衰减振荡函数s2的幅值为A2=150，频率为f2=50 MHz；两种放电信号均在同一时刻发生，共取2 000个采样点。局部放电信号仿真波形如图2所示。

图2 局部放电仿真信号Fig.2 Partial discharge simulation signal

分别以第900个和第1 000个点作为矩形窗的截断点将原放电信号分成两段。两种情况下分别对两个子段数据进行VMD(K=2)，并将两子段的各模态分量直接拼接重构，各重构模态分量在截断处的放大图如图3和图4所示。由图可知，信号整体分解得到的模态分量与原信号分量基本吻合；而原信号截断，各子段模态分量直接拼接重构时，在截断处不连续，且在截断处附近出现较大的误差。此外，比较图3和图4两种情况可知，以第1 000个点为截断点时的子段模态分量直接拼接重构的误差远小于以第900个点为截断点的子段模态分量直接拼接重构的误差。这是因为第1 000个点两侧信号值变化较平稳，信号值差异较小。由此可知，子段数据拼接重构时的误差大小主要取决于截断点前后信号值差异的大小。截断点前后信号值越平稳，变化越小，拼接重构后模态分量的误差越小，反之，则越大。

图3 第900数据点作为截断点时VMD分解的模态分量Fig.3 Modal components by VMD with 900th data point as cut point

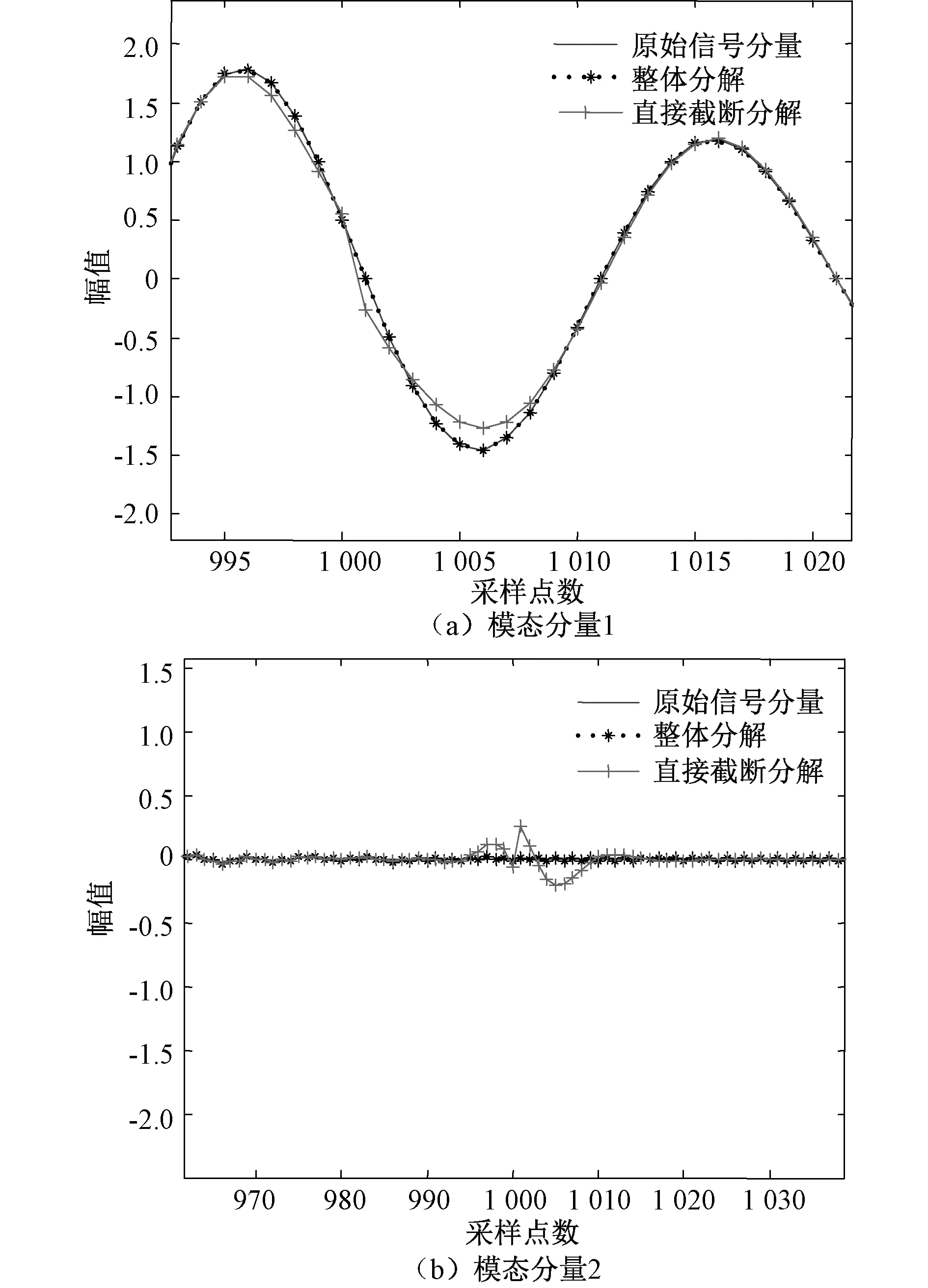
图4 第1 000数据点作为截断点时VMD分解的模态分量Fig.4 Modal components by VMD with 1 000th data point as cut point

2.3 基于ASLF-E和VMD-RWS的并行VMD算法

由于矩形窗截断点前后信号的平稳程度会影响子段模态分量的重构精度，为了选择较平稳的点作为窗口截断点，本文提出了一种基于信号局部平稳度的自适应数据分段方法。

信号局部平稳度δi定量描述信号中某个点xi附近信号值变化相对于整体信号的剧烈程度，是一个相对的概念。对于长度为l的信号局部{xi-|l/2|,xi-|l/2|+2,…,xi-1,xi,xi+1,…,xi+|l/2|}，δi如下[18]：

(10)

式中：E为信号总体的均值；l为信号局部的长度(是奇数)；Ei为信号局部均值，如式(11)所示。

(11)

若δi>1，表示信号局部差异大于信号总体差异，以xi作为窗口截断点时子段数据VMD分解的模态分量进行拼接重构时会产生较大的误差；若δi<=1，表示信号局部差异与信号总体差异相比较小，适合作为窗口截断点。

电力设备监测信号经矩形窗截断得到若干子段数据，由于VMD算法存在边界效应，窗口截断处以及原信号两端若不进行补偿，对各子段数据直接进行VMD分解，并将各子段模态分量直接进行拼接重构，会在窗口截断处和原始信号两端产生较大的误差，并在窗口截断处产生不连续。

考虑到VMD算法的边界效应和矩形窗函数的固有缺陷，本文提出基于ASLF-E和VMD-RWS的放电信号分析方法，采用ASLF-E方法对原始放电信号进行自适应分段和子段数据的外推延拓处理，然后对处理后的各子段数据分别进行VMD分解，最后根据各子段矩形窗大小对所得子段各模态分量进行裁切，并将各子段模态分量依次拼接重构得到原信号的模态分量，从而保证在窗口截断处连续。

基于ASLF-E的并行VMD算法的具体实现步骤如下：

步骤1：确定原信号截断矩形窗的个数l，将原信号等分为l个子段数据，初步确定l-1 个窗口截断点xcut(h)(h=1,2, …,l-1)及其相应的下标索引xcut_index(h)。

步骤2：依次计算以各截断点xcut(h)(h=1,2, …,l-1)为中心的信号局部平稳度δh，信号局部长度为步骤1中平分子段数据长度。若δh<=1，则将该点作为窗口截断点；否则在该点在所属平分子段范围内依次向后逐点计算信号局部平稳度，直到找到δh<=1 的点，将该点作为窗口截断点。若该平分子段数据内各点均不满足δh<=1，则将该平分子段数据中平稳度最小的点作为窗口截断点。记录相应窗口截断点的下标索引和相应矩形窗长度。

步骤3：根据步骤2中得到的窗口截断点，将原信号分成l个长度不等的子段数据。

步骤4：将第一个子段数据的左侧和最后一个子段数据的右侧分别进行镜像延拓，延拓长度为所属子段数据长度的一半。其余各子段数据边界处采用与该子段相邻的原数据进行外推延拓，延拓长度均为所属子段长度的一半。

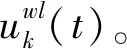
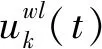
为了验证ASLF-E的边界补偿方法的有效性，分别采用基于ASLF-E和VMD-RWS方法、直接采用VMD-RWS方法以及基于信号局部平稳度的自适应分段的VMD-RWS方法对图2所示的仿真放电信号进行分析，三种方法截断矩形窗个数均为4个，分解层数为K=2。将由三种方法得到的模态分量分别与整体分解(信号两端均进行了镜像延拓)得到的模态分量进行比较，各模态分量重构误差如图5所示，三种方法模态分量重构和信号重构误差如表1所示。

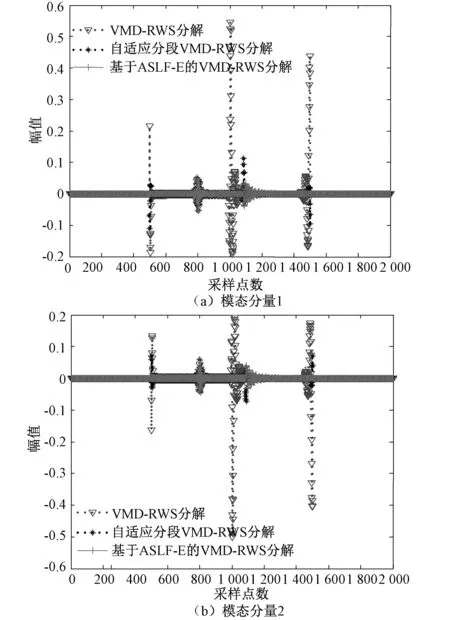
图5 模态分量重构误差Fig.5 Errors of reconstructed modal components

表1 重构模态分量和重构信号的误差

Tab.1 Errors of reconstructed modal components and reconstructed signals

分析方法模态分量1模态分量2重构信号VMD-RWS15.509 116.008 16.671 0基于自适应分段VMD-RWS3.889 24.921 35.959 9基于ASLF-E和VMD-RWS3.120 63.759 73.349 5

由图5和表1可以知，采用VMD-RWS方法的模态分量重构误差远大于基于自适应分段的VMD-RWS方法的模态分量重构误差，这是因为基于自适应分段的VMD-RWS方法选择前后信号较平稳度的点作为窗口截断点，因而模态重构误差相对较小。而基于ASLF-E和VMD-RWS方法的模态重构误差(尤其在截断点处)小于基于自适应分段的VMD-RWS方法的模态分量重构误差，这是因为基于ASLF-E和VMD-RWS方法对各子段数据两端进行了外推延拓，因而只会在外推后的数据信息边界处产生边界效应，而在原窗口截断处抑制了边界效应造成的较大误差。实验结果表明，基于ASLF-E和VMD-RWS方法可以有效实现放电信号的分段处理，可抑制原信号两端和窗口截断处的边界效应。因此，本文所提方法可以实现在云平台上进行并行分析。

3 基于Storm/Spark云平台下的并行VMD算法

为了有效处理数据量较大的电力监测信号，本文提出一种基于Storm/Spark云平台下的并行VMD算法。

图6为基于Storm云平台下的并行VMD算法的处理流程。Spout组件将采集的实时电力设备监测信号采用基于信号局部平稳度的自适应数据分段方法进行分段，并对每个子段数据进行外推延拓处理，之后将各处理后的子段以tuple元组形式发送给各处理组件(Bolt)进行并行VMD分析。各子段的并行分析结果最终由Bolt组件进行无缝合并，得到原始采样数据的VMD处理结果，然后在此基础上再进行信号分析处理(如特征提取等)。

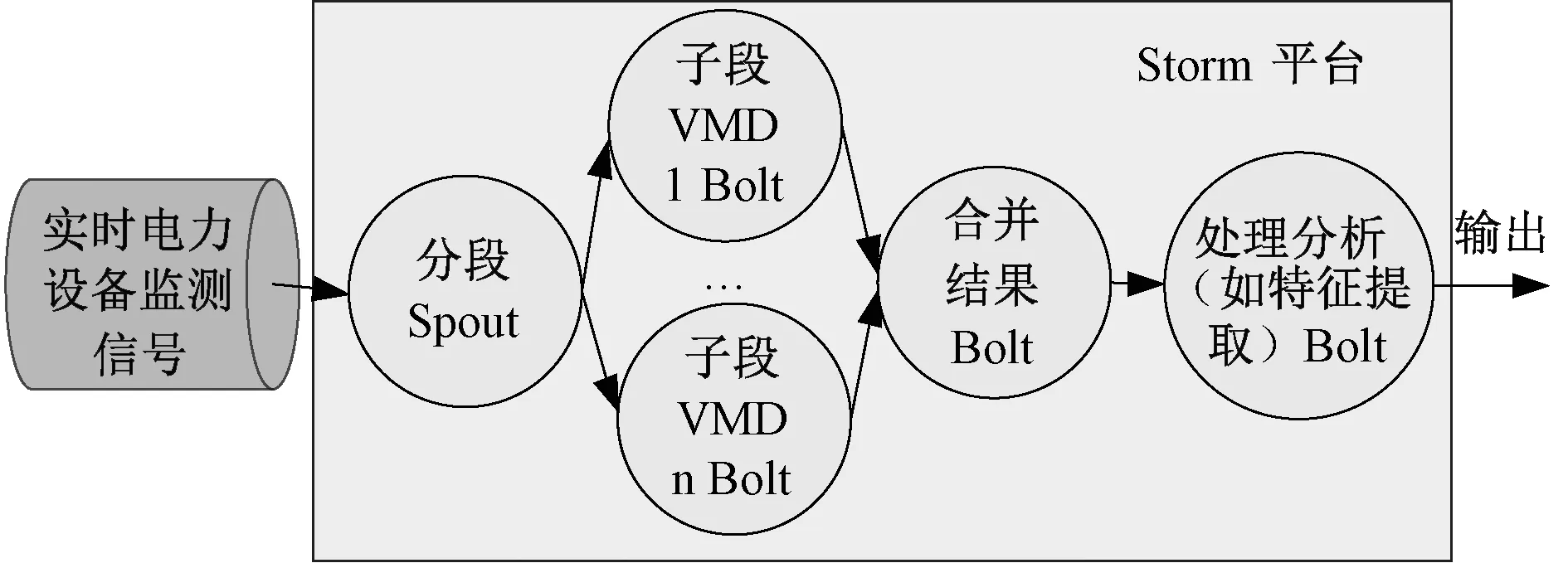
图6 基于Storm云平台下的并行VMD算法Fig.6 Parallel VMD algorithm based on Storm cloud platform

图7为基于Spark平台下的并行VMD算法的处理流程。其功能是对HDFS文件系统中历史电力设备监测信号采用VMD算法进行分析，对分解结果进行处理(如特征提取)最终实现信号的分析处理。在Spark平台上将历史监测信号采用基于信号局部平稳度的自适应数据分段方法进行分段，并将各子段分发到多个节点上，由各节点并行对各子段进行VMD分析，各子段的并行VMD分析结果最终无缝合并为原始信号的分析结果，根据需要对VMD分析结果进行处理(如特征提取)。

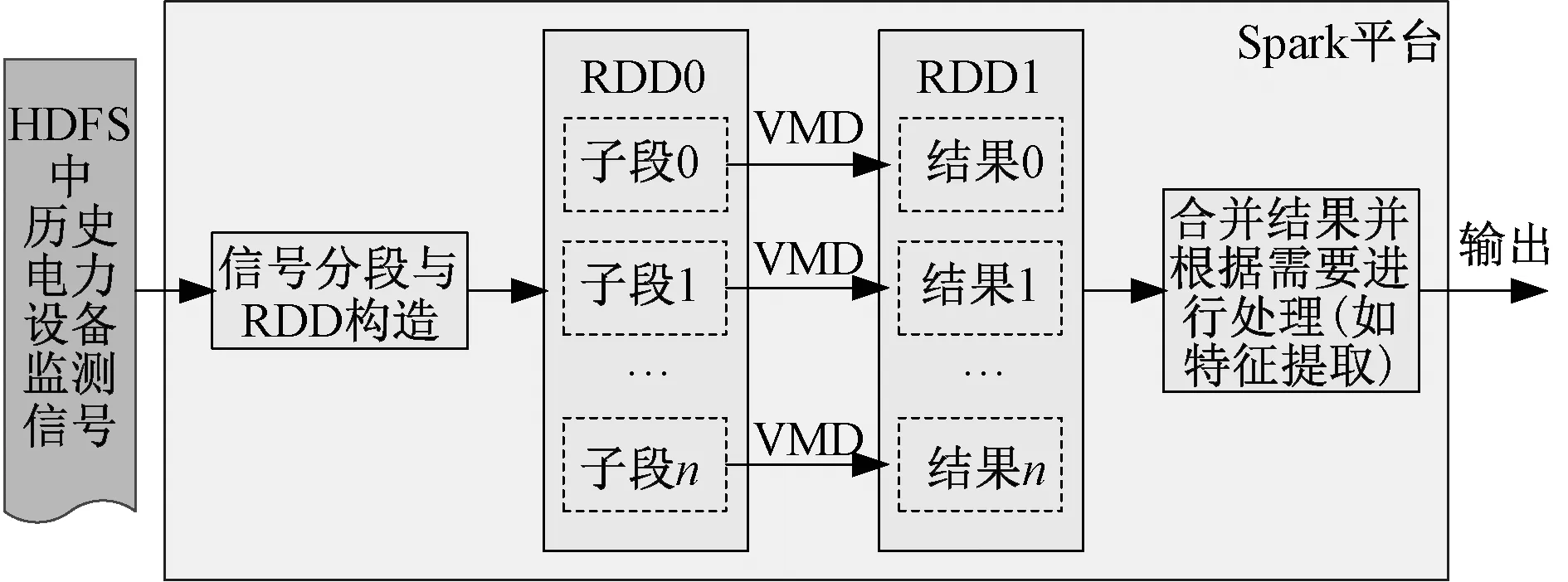
图7 基于Spark云平台下的并行VMD算法Fig.7 Parallel VMD algorithm based on Spark cloud platform

上述方法可将较长的电力设备监测信号进行分段，并将子信号段分发到Storm和Spark云平台上的可用计算节点上并行执行，这对于一个信号的分析处理的耗时缩减虽并不明显，但在某时刻当电网井喷式报警的若干波形信号同时到来时，Storm云平台能对这些信号生成大量的信号分段处理任务，并通过任务调度策略自动调度到平台的各个节点上。这样，Storm云平台对于几乎同时带来的诸多波形信号能在极短的时间内得到处理，使得后续的大量电力设备监测信号能得到及时处理。

4 结 论

在电力设备监测数据中很大一部分是时序波形信号数据，这些数据是用来评估电力设备运行状态的重要依据。VMD算法是一种完全非递归的变分模态分解方法，适用于对非线性、非平稳信号的分析。但VMD算法的计算过程很复杂、运算量大，属于计算密集型任务，当面临大量的波形信号时，处理效率低，因此本文基于Storm/Spark平台进行VMD 算法的并行优化研究，结论如下：

(1)提出了一种基于矩形窗分段的变分模态分解(Variational Mode Decomposition，VMD)VMD-RWS和基于自适应分段和外推延拓(the adaptive subsection based on local flatness and extrapolation，ASLF-E)ASLF-E的信号处理方法进行信号分段以及子段数据处理，以确保各子段数据模态分量在窗口截断处连续，论证了VMD算法在Storm/Spark平台云平台上并行分析的可行性。

(2)设计了基于Storm和Spark平台的并行VMD算法处理流程及架构，为基于云平台的并行VMD算法的实现提供了依据。

对于数据量较大的电气设备监测信号，在云平台下采用基于ASLF-E和VMD-RWS方法可大大缩短信号的处理时间，及时实现电力设备监测信号基于VMD算法的分析处理(如去噪、特征提取、时频分析等)，这对于信号的分析处理具有重要意义，这也为泛在电力物联网提供了有力的技术支持。