基于Gumbel copula联合概率分布的电力系统综合净负荷预测

陶 鹏， 牛为华， 吴宏波， 任 鹏

(1.国网河北省电力有限公司电力科学研究院，河北 石家庄 050021； 2.华北电力大学 控制与计算机工程学院，河北 保定 071003)

0 引 言

在传统电力系统中，负荷往往是唯一的不确定运行变量，发电规划等通常需依赖于负荷预测来进行。然而现代电力系统包含大量的可再生能源，如风能和太阳能。这些可再生发电过程中将伴随含有不确定性和间歇性的变量，从而对系统运行规划提出更高的复杂性要求和挑战。不同的不确定变量，如负荷、风能和太阳能发电等可遵循不确定变量规律，即净负荷。净负荷是通过取总负荷和可再生能源发电的差来进行预估的，其属于系统的有效负荷。因此，传统发电机组需依据净负荷来进行投入[1]。有关净负荷的优先信息可有效支撑系统运行，如发电规划等。类似的优先净负荷信息可通过净负荷预测(net load forecasting，NLF)得到。

过去几十年中，在负荷预测[2-4]和可再生能源出力预测[5-6]方面已有多项研究取得重大突破。然而，尽管净负荷预测对电力系统运行规划如发电规划和现代电力系统灵活性需求预估具有重要意义，对于NLF的研究却还尚未深入开展[7]。负荷预测可通过两种不同方式实现：直接法和联合预估法[7]。直接预估法将以往的净负荷时间序列用以进行净负荷预估。在对外部因素如温度，湿度，气压和风速的筛选过程中，直接NLF的精确性将随其开展而降低，因此，净负荷是多种变量的集合，且不同变量存在不同的决定因素。联合净负荷预测可以通过联合不同负荷和可再生能源发电预测进行预测，也可通过单个预测误差进行估算。单个负荷和可再生能源发电预测可通过不同的预测模型得到。在现有文献中已经论述了多种通过寻找外部参数从而对负荷和可再生能源进行预测的方法，其中，联合NLF方法可对净负荷预测提供更准确的预估[7]。

从单个负荷、风能和太阳能发电预测所获取的联合净负荷预测存在预测误差。此类对单个预估量的弱预估造成了净负荷的不确定性，而不确定性的叠加将造成同方向的净负荷预测存在较大误差，从而造成负荷发电的失衡和经济损失。因此，净负荷的不确定性精确建模就迫在眉睫。对负荷、风能和太阳能预估误差的联合概率分布(Joint Probability Distribution，JPD)可用于对净负荷不确定性的估算[8]。Gumbel copula适用于由大稳定特性所产生的依赖于极端负荷、风能和太阳能预测错误事件的建模。极端预测误差的叠加将造成系统的不平衡性。因此，利用Gumbel copula JPD进行预测需覆盖负荷的所有极端情况且保证负荷发电在所有条件下保持平衡。

此外，为解决新能源发电过程中不确定性和参数多样性等问题，发电规划过程中的系统运行策略应尽可能提前5分钟制定[9]。此类方法保证了对于短期的NLF模型的快速和准确性需求。对于此类高速NLF模型，则可采用对于量子训练数据时间要求低的预测模型。训练数据要求也可通过选取最佳输入预测参数进行相应降低。关联分析则可用于不同预测模型中以作为特征选取技术进行应用。

本文提出了一种新型短期NLF模型，其中净负荷不确定性可通过采用基于负荷、风能和太阳能发电预测误差JPD的Gumbel copula进行模拟。所提模型引入了Grey系统理论。由于其动能转移特性，基于Grey系统理论的模型需要采集低量子训练数据[10]。最终实验结果表明所提方法在短期净负荷精确预测中的有效性。

1 NLF 模型

所提NLF模型应用了四种类型的NLF：直接型，初始型，间断型和连续型。其中，直接型采用单因素预测法且采用历史净负荷时间序列作为输入数据；初始型净负荷预测可以通过对负荷预测和总太阳能和风能发电预测的差进行估算。在初始型中，负荷和可再生能源发电预估误差可被忽略。单个负荷和可再生能源发电预测可通过采用天气变量和历史数据的多因素预测获得；间断型需要考虑负荷和可再生能源发电预测误差。在各时间步长下的仿真正负预测误差和初始净负荷预测将被用以产生间隔型预测。间隔上限可通过初始预测和仿真正误差之和得到，而间隔的下限可通过初始预测和仿真负误差得到。联合净负荷预测可通过上下限的均值预估得到。

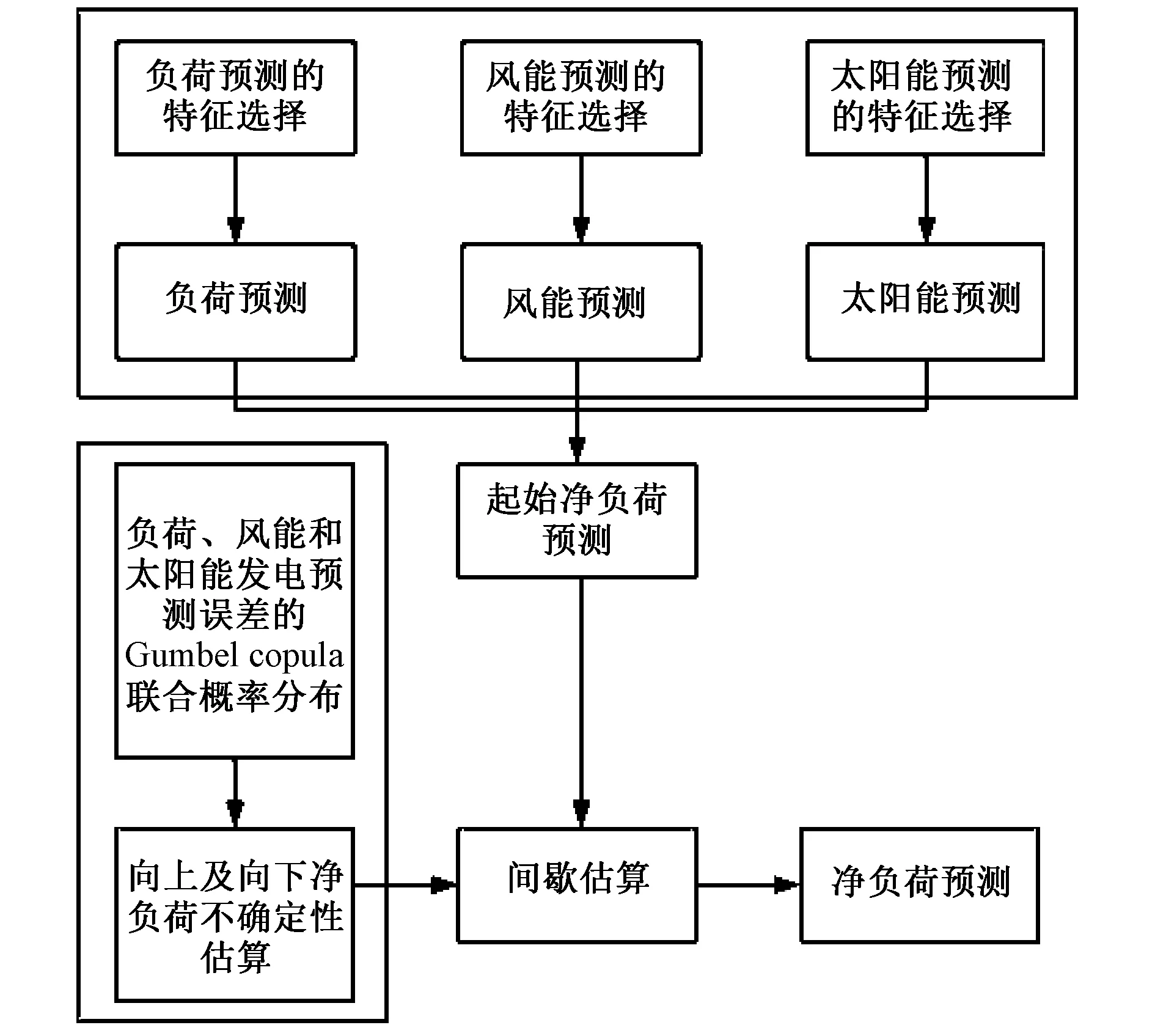
图1 NLF模型Fig.1 Proposed NLF model

所提模型主要包含三个阶段，如图1所示。第一阶段包含短期负荷、风能和太阳能的出力预测。修正的Grey指数模型可用于极短期负荷、风能和太阳能出力预测。净负荷不确定性是负荷、风能和太阳能发电不确定性的函数。该函数需要三者不确定性的联合概率估算。

第二阶段可通过估算的JPD对净负荷不确定性进行预测。净负荷不确定性可分为两个部分，向上和向下净负荷不确定性，其分别可通过分别计算JPD左半部和右半部的标准偏差估算得到。

第三阶段结果是通过结合前两个阶段结果得到的。其通过对负荷和可再生能源出力求差得到了初始净负荷预测。在此之后，间断型预测分别通过对初始端预测的向上/向下不确定性的加减进行计算。最终将每个时间步长联合净负荷预测作为同一时间步长间断预测的均值。

1.1 修正的Grey指数模型

模型选择对预测而言非常重要，通常需基于数据类型。短期预测指的是预测范围在分钟级别或数据前几分钟进行的预测。在该时间范围下的负荷、风能和太阳能发电数据显示出强自相关性。因此，采用历史数据的预测模型可用于短期预测。基于Grey系统理论的仿真模型可传输发生于过去数据库的动能情况。该特点可降低输入数据需求且表现出较强的短期预测能力。负荷、风能和太阳能发电与气候参数如温度，气压和湿度之间具有强相关性。在考虑该关联性的基础上，本论文通过联合参数选择，提出了基于Grey系统理论的修正模型。其可通过对输入变量数目和微分方程的阶次不同分为不同的Grey指数模型。修正的Grey指数模型流程图如图2所示。

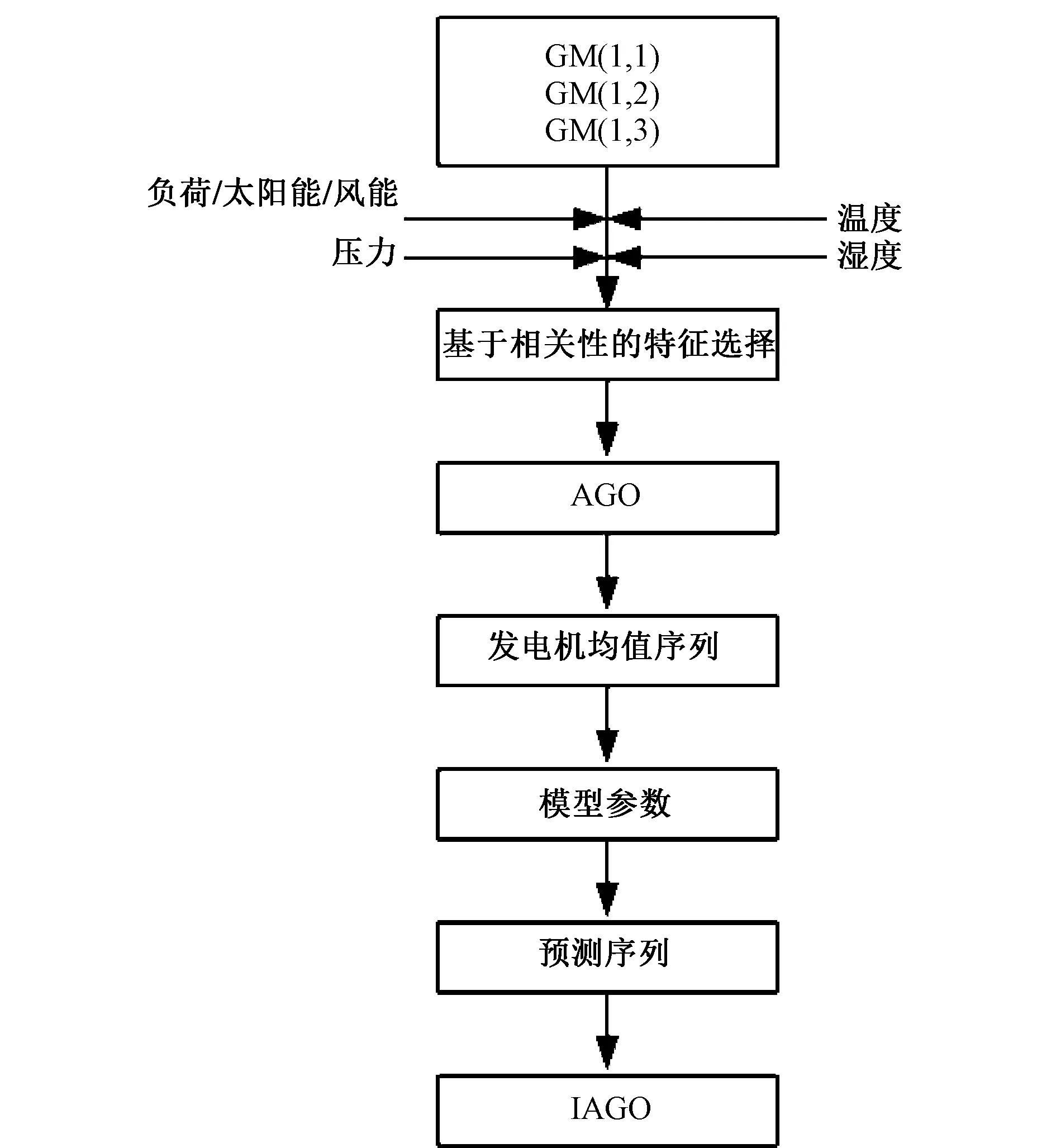
图2 修正Grey指数模型流程图Fig.2 Modified grey index model

用户的单因素，双因素和三因素Grey指数模型选择应基于对该模型的精确度和速度需求。鉴于模型的兼容性，基于联合特征参数的选择有助于选择强相关输入的参数。因此，只有历史负荷和可再生能源数据可用以单因素变量模型。在双因素模型中，主要采用具有强关联的气候参数和历史负荷及可再生能源出力数据。三因素模型则采用两个强关联的气候参数和历史负荷或发电值。所选输入信号将进行累积生成(accumulated generated operation，AGO)法，用以为模型参数估算生成均值序列。可预测序列则通过AGO的逆推得到(inverse accumulated generated operation，IAGO)。上述单因素，双因素和三因素模型可应用于短期负荷、风能和太阳能发电预测。

1.2 联合特征选择

所提模型采用了两种相关模型：Gumbel copula模型和联合分析模型。Gumbel copula模型用以集合负荷、风能和太阳能预测误差；而联合分析模型用以寻找最佳气候变量，从而作为负荷、风能和太阳能预测的外部输入。该三者与不同的气候参数密切相关，随着外部条件而相应改变。因为强相关的特征值有助于获取更加精确的预测，因此负荷和可再生能源发电与其相关的气候变量之间的关系可作为负荷和可再生能源出力预测的输入特征值。具体相关性可通过Pearson关联函数计算得到：

(1)

式中：Hmean为平均负荷功率/可再生能源出力；CFmean为气候参数平均值；Ht、CFt分别为时刻t的负荷功率/可再生能源出力和气候参数。鉴于所提预测模型的兼容性，各季节下具有强关联性的气候参数可通过输入特征值进行选取。

1.3 单因素Grey模型(GM(1，1))

Grey一阶变量模型(GM(1，1))属于时间序列单变量预测模型，其不需要进行关联特征值选取。模型中的微分方程需要时间变化系数，且其只可应用于正数序列[11]。由于负荷和可再生能源发电数据总为正，因此基于预测的Grey系统可应用于太阳辐照。AGO可通过产生单向增长的时间序列数据用于减少数据的任意性。系统的时间变化系数可通过模型微分方程求解，从而在t+1时刻用以预测AGO数据。IAGO则将集成的时间序列进行转换用以估算实际的时间序列，从而从预测的AGO值中获取实际估算的预测值。

考虑到历史数据序列集合S0，S0表示n个5 min时间范围的负荷和可再生能源序列集合，表示如下：

S0=(S0(1),S0(2),S0(3),…,S0(n))

(2)

历史负荷和可再生能源发电数据序列可通过AGO转换成单一增长的序列：

S1=(S1(1),S1(2),S1(3),…,S1(n))

(3)

其中

(4)

Grey微分方程的最小二乘估计序列GM(1，1)可通过历史负荷或可再生能源发电数据序列S0和生成的均值序列I1仿真得到，具体如下所示：

S0(t)+αI1(t)=β

(5)

发电机均值序列与AGO输出历史数据序列相关，可写为

I1=[I1(1),I1(2),I1(3),…,I1(n)]

(6)

其中I1是附和AGO数据的均值。

I1(t)=0.5(S1(t)+S1(t-1))

(7)

与所给历史数据集合相关的拓展方程如下：

(8)

模型参数可被估算为

(9)

其中：

Y=[S1(2),S1(3),…,S1(n)]T

(10)

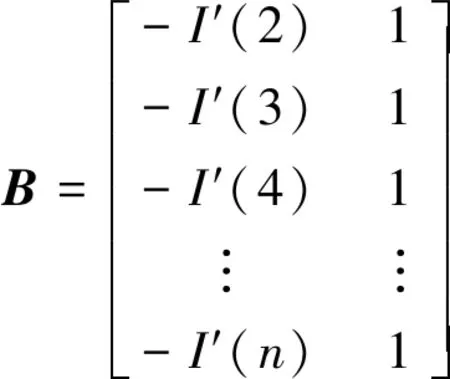
(11)

若使得在时间t+1时刻的数值单向增长，则

(12)

IAGO用以获取在t+1时刻的实际值。在时刻t+1时刻的预测值为

(13)

单因素模型仅采用历史数据，与预测量具有高相关性的额外参数可用于进一步提高系统准确度。

1.4 双因素Grey模型(GM(1，2))

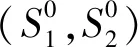
(14)

模型参数估算值如下：

(15)

其中

Y=[S1(2),S1(3),…,S1(n)]T

(16)

(17)

在时刻t+1单向增长的值如下：

(18)

在t+1时刻，从AGO预测联合值中通过IAGO算法获得实际预估值[11]，

(19)

与预测变量有强关联性的额外外部输入特征值可进一步增加系统的精确度，因此GM(1，3)模型将采用两种外部特征值作为输入进行预测。

1.5 三因素Grey模型(GM(1，3))

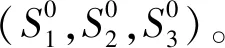
(20)

其中，α、β1、β2和β3是模型参数。这些参数可以如下形式进行估算：

(21)

其中

Y=[S1(2),S1(3),…,S1(n)]T

(22)

(23)

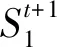
(24)

在t+1时刻，通过IAGO算法从AGO联合预测值中获得实际预估值：

(25)

由上述模型得到的负荷和可再生能源发电预测可用以净负荷预测估算。

1.6 净负荷不确定性估算

负荷和可再生能源预测存在正误差和负误差，因此NLF应该将正负方向的净负荷不确定性均考虑在内。正负净负荷不确定性可通过NLF误差分布的左右两侧进行预估。NLF误差分布可通过采用负荷、风能和太阳能预测误差的JPD样本进行仿真。NLF误差分布如下：

Z=L-(X+Y

(26)

其中L、X、Y、Z分别为与负荷、风、光伏和净负荷预测误差相对应的随机变量。

JPD可通过Copula理论进行估算。Copula是一个通过预先指定边际分布在随机变量中产生多变量分布的函数。当方程C：[0 1]3→[0 1]时，若满足下列条件，则三变量copula函数成立。

(1)当u1=0或u2=0或u3=0时，C(u1,u2,u3)=0；

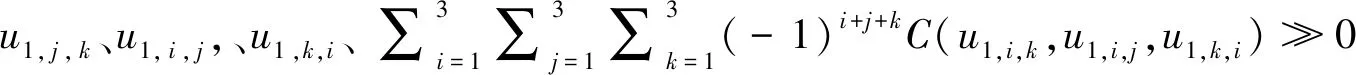
(3)对所有[0, 1]范围内的u1、u2和u3，满足C(u1,1,1)=u1；C(1,u2,1)=u3；C(1,1,u1)=u3。

斯克拉尔定理定义了JPD和copula方程之间的关系。根据斯克拉尔定理，三个边际分布JPD方程(F1,F2和F3)以及所给的copula方程C对所有的η1、η2和η3可写为

F1,2,3(η1,η2,η3)=C(F(η1),F(η2),F(η3);θ)=

C(u1,u2,u3;θ)

(27)

式中：θ为Copula方程依赖因子。

基于JPD Gumbel copula的负载，风能和太阳能出力误差可表示为

最后是人物刻画的鲜明性，戏剧是以事写人的艺术，同时也需要接受人的观赏。因此，人物的描写合理性就显得十分必要，“生旦有生旦之体，净丑有净丑之脸”是首要，为了突出人物特色，李渔还主张可以对人物进行适当的角色限制，使其鲜明，［5］情境的描写和对应的旁白映衬人物心理也是一大创新。在当代，不论电视剧还是电影剧本的创作，都必须遵从这一人物刻画的原则。

H(L,X,Y)=C(Fl(L),Fx(-X),Fy(-Y))=

(28)

式中：H(·)为误差计算方程。

Gumbel参数ε可通过采用最大可能估计进行估算。JPD结果的概率密度方程如下所示：

(29)

式中：hΘ(·)为JPD概率密度方程。

JPD样本可通过对式(29)进行采样得到。所得预测误差样本可用以Z函数估算。净负荷在t时刻的正不确定性可基于t时刻的Z分布的右侧标准差进行仿真，负不确定性则可基于Z分布在t时刻左半边的标准差进行仿真。

(30)

(31)

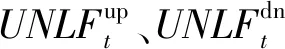
1.7 联合NLF

NLF间隔可通过编译初始净负荷预测和向上/下净负荷不确定性浮动值综合获得。初始净负荷预测可通过取负荷预测和总可再生能源发电预测之差获得。

PNLFt=LFt-(SFt+WFt)

(32)

式中：PNLFt为t时刻净负荷初始预测值；LFt为t时刻负荷预测；SFt、WFt分别为t时刻太阳能、风能出力预测。

向上净负荷预测可通过在初始净负荷预测上加向上净负荷不确定性获得，向下净负荷预测可通过在初始净负荷预测上减去向下净负荷不确定性获得。

(33)

(34)

净负荷的点预测可通过在各时间步长上取间隔预测均值得到。

(35)

式中：NLFt为考虑不确定情况下，t时刻净负荷预测值。

直接NLF的方法论如图3所示。净负荷时间序列如下：

NLt=Lt-(SGt+WGt)

(36)

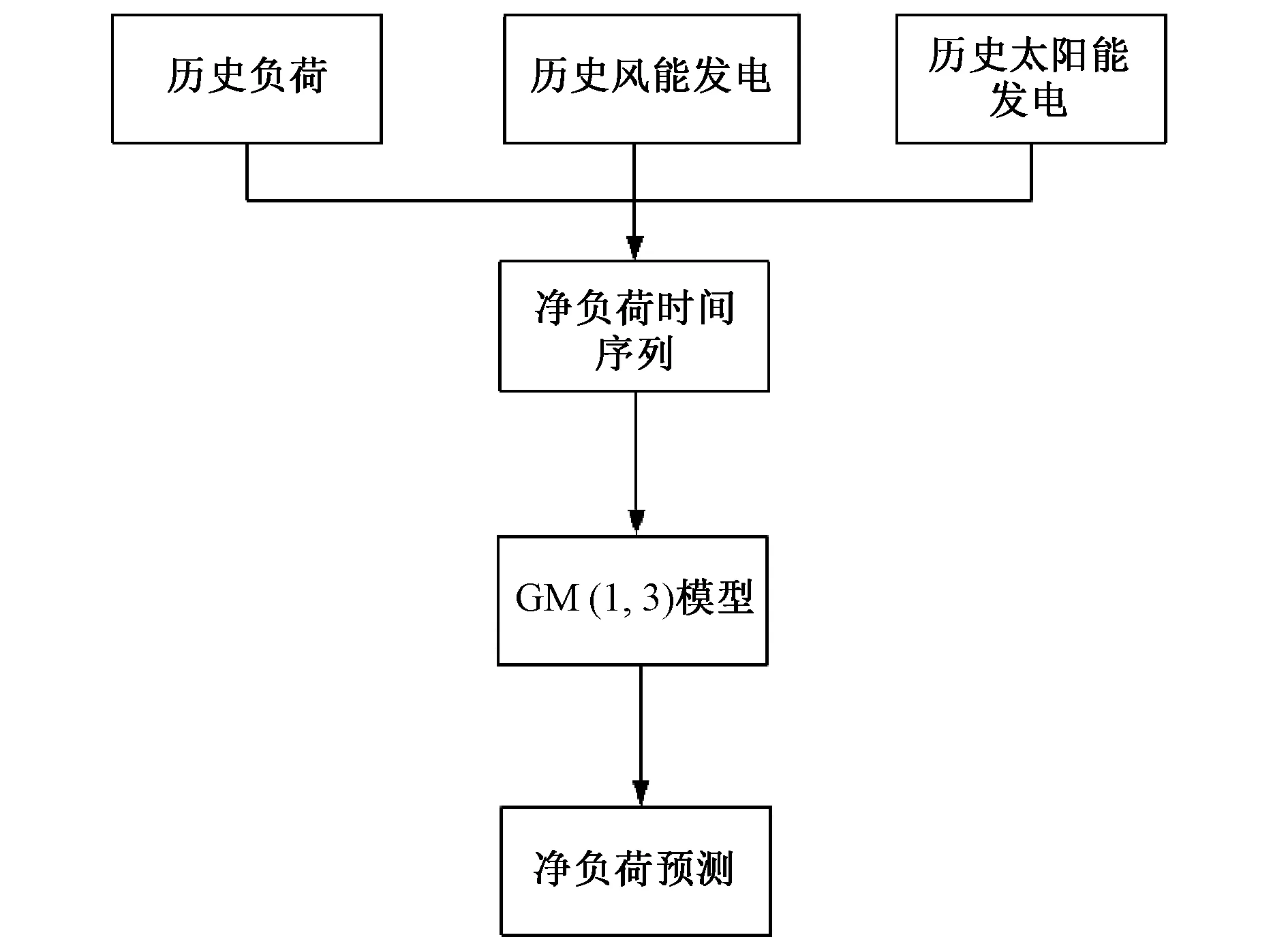
图3 直接NLF模型Fig.3 Direct NLF model

2 预测模型及性能

预测性能可通过参数估算得到，例如平均绝对误差(mean absolute error，MAE)和平均绝对百分比误差(mean absolute percentage error，MAPE)等。MAE是绝对误差t在任意时刻的均值，

(37)

百分比误差是绝对误差和在任意时刻实际值的比值，具体如下：

(38)

MAPE是百分比误差PE(t)的均值，具体如下：

(39)

通过性能参数和基本模型的对比可知通过参考模型预测所得体现所提模型预测的优越性。SVR初始模型和直接NLF模型可用以作为基础模型来对比预测性能。鉴于SVR模型近年来所体现的预测效果通常优于其他人工神经系统模型，其被广泛应用于各类预测研究中。其可应用于单个负荷、风能和太阳能发电预测，但在所提方法的Grey指数模型中并不适用。

为保证理想的模型性能，可进一步计算剩余相关量。若剩余参数存在关联，则剩余参数存在信息量，且应被应用于预测中。因此，预测模型需要检查剩余量的关联性以保证系统最佳性能。其中，ACF和PACF都可用于估算剩余量关联性。

3 算例分析

本文采用博纳维尔电力公司辖区五分钟内的负荷和风电数据进行NLF测试[12]。所选系统含有13 500 MW的平均负荷。该区域内同时安装了容量为4 500 MW的风电机组。

所提模型采用过去的每小时数据和外部环境数据作为输入。同时将实际数据通过AGO转换成单一增长数据。因此，数据参数并非从实际历史小时数据进行估算的，而是通过历史小时AGO数据估算得到。故充分性测试是在负荷、风能和太阳能发电的AGO数据上进行开展的。相应的历史小时单向增长AGO数据和ACF图如图4-6所示。结果表明三者的AGO数据具有强自相关性和移动特性。因此，传输AGO数据动能的模型可用以进行预测。伴随非序列相关的零假设，Ljung-Box数据可用以对相同采用计算ACF数据的数据库进行估算。负荷、风能和太阳能发电AGO数据的Ljung-Box测试数据Q分别是58.88，65.28和64.24。这些值将和临界平方分布差值3.841在5%的显著水平进行比较。所有的Q值都要明显大于临界平均分布方差值。因此，对应的历史数据模型可用以进行精确预测。

所提方法采用了冬季，换季和夏季三个季节用来评估在不同季节影响下的系统预测性能。单个负荷、风能和太阳能发电预测是所提NLF模型的第一步。修正Grey指数模型采用基于相关性的特征选择进行预测。

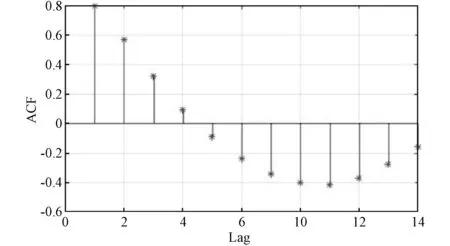
图4 负荷数据ACF图Fig.4 ACF plot of load data

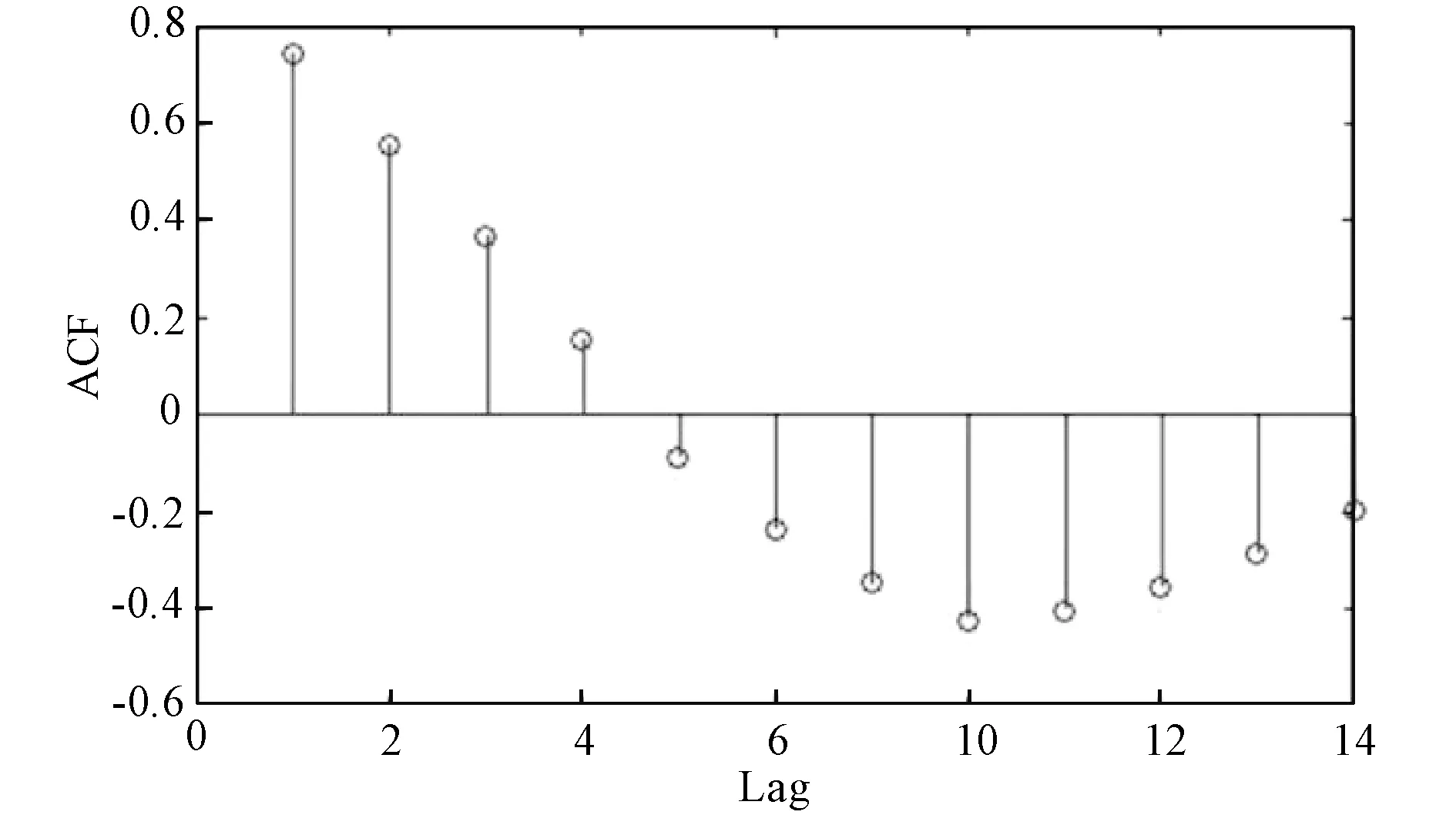
图5 风能数据ACF图Fig.5 ACF plot of wind data

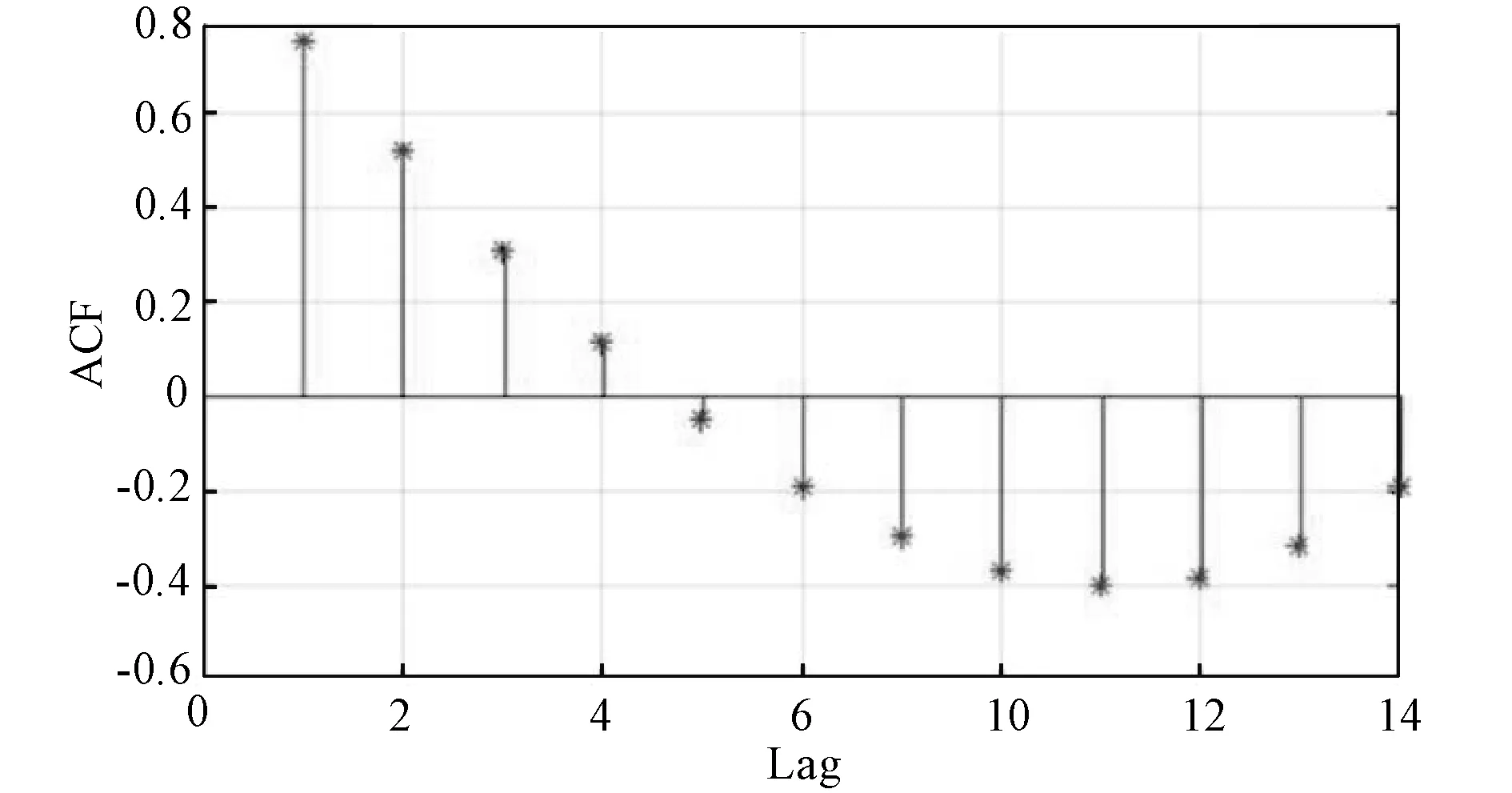
图6 光伏数据ACF图Fig.6 ACF plot of solar data

3.1 对外部环境输入选择的相关性分析

短期负荷、风能和太阳能发电与不同气候参数的不同季节净负荷的相关性关系如表1所示。负荷和气候参数如温度，湿度和风速等参数具有强相关性，且该关系随着季节而变化。负荷和温度在冬季表现出负相关性是由于温度增加将减少负荷发热。在夏季，负荷和温度呈正相关，这是由于冷负荷的热量增加。换季期间体现出正相关，相关系数为0.37。湿度在所有季节都和负荷呈负相关。湿度对负荷的影响在冬天可忽略，在夏天和换季期间，高湿度将引起实际体感温度的增加。风速在夏天和冬天分别体现正相关和负相关。在换季期间体现正相关且相关系数为0.16。因此GM(1，1)模型仅采用历史负荷值进行三季负荷预测。GM(1，2)模型在冬季和换季期间采用历史负荷数据和温度数据，在夏季采用历史负荷数据和湿度数据。GM(1，3)则参考SVR模型采用历史负荷数据、温度和风速数据进行冬季负荷预测。历史负荷、温度和湿度将用于换季和夏天进行预测。

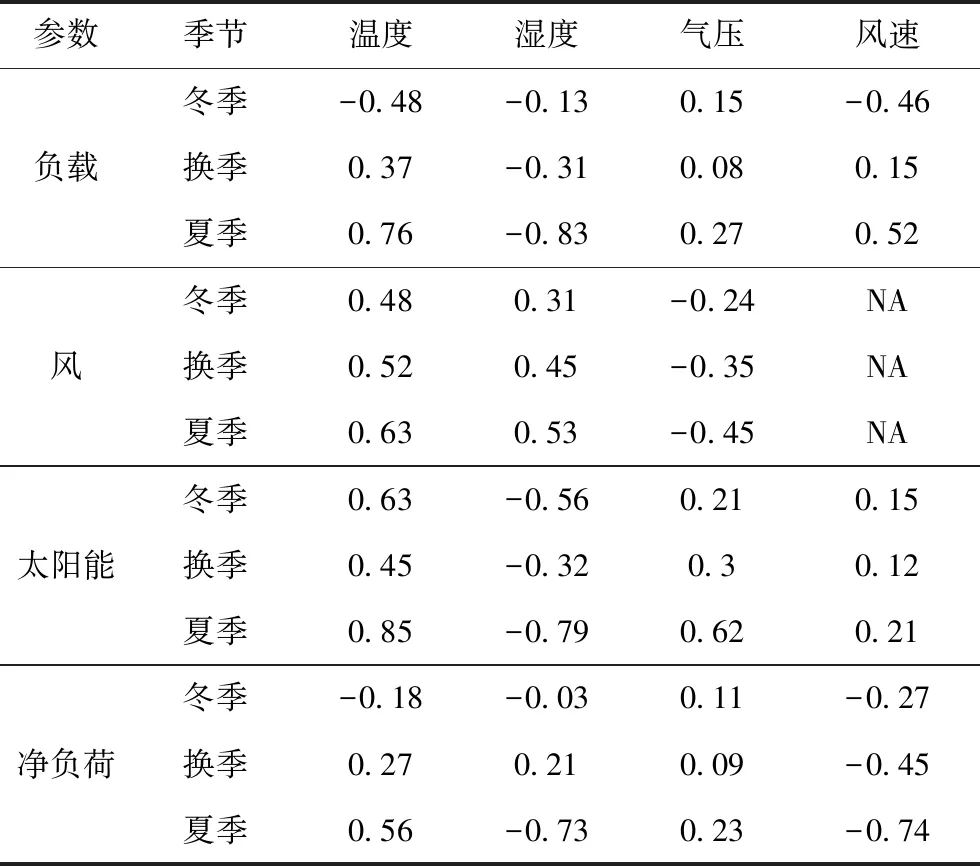
表1 外部输入选择的关联性分析

太阳能与温度呈强正相关，和气压呈弱正相关，和湿度呈强负相关。相关性伴随季节产生变化，夏天呈现强相关性，而换季期间呈现弱相关性。这是由于夏季太阳透射程度更高，而换季期间气候参数会产生不规则变化。由于湿度和温度与太阳能呈强相关性，湿度和温度以及历史太阳能将作为GM(1，2)，GM(1，3)和参考SVR模型的输入参数。GM(1，1)模型则仅采用历史太阳能数据作为三季预测的输入参数。

由于风将从高温度梯度地区吹向低温度梯度地区，高湿度地区向低湿度地区，高压地区吹向低压地区，因此，风能在三季和温度及湿度呈现正相关，和压力呈现负相关。因此，GM(1，2)模型在三季采用温度和历史风能作为外部参数。GM(1，3)和参考SVR模型采用温度，湿度以及风速在三季作为外部输入参数。

对直接模型的NLF外部参数可通过相关性分析获得。净负荷在换季和夏季期间与温度呈现正相关，在冬季呈现负相关。相关性系数和负荷相比，其值将因为净负荷中存在可再生能源发电的影响而更小。在夏季与湿度呈现强负相关性，在换季期间呈现弱负相关性，在冬季无明显相关性呈现。风速和净负荷在三季期间均体现负相关性，这是由于风速的增加将导致风能发电增加，从而减少净负荷。因此，直接NLF模型将采用温度和风速以及净负荷时间序列作为外部输入。

3.2 初始NLF

初始净负荷预测可通过对比单个负荷预测与单个太阳能和风能预测的差异获得，如式(36)所示。不同季节的时间参数(早、中、傍晚、夜间)将用以进行分析，体现在不同天数或年份下不同模型的性能。MAE和MAPE在不同季节的早间(早9.00 am -早10.00 am)，中午(午12.00 pm到午 1.00 pm)，傍晚(晚4.00 pm 到晚5.00 pm)及晚间(晚10.00 pm到晚 11.00 pm)小时初始净负荷预测分别如表2和3所示。

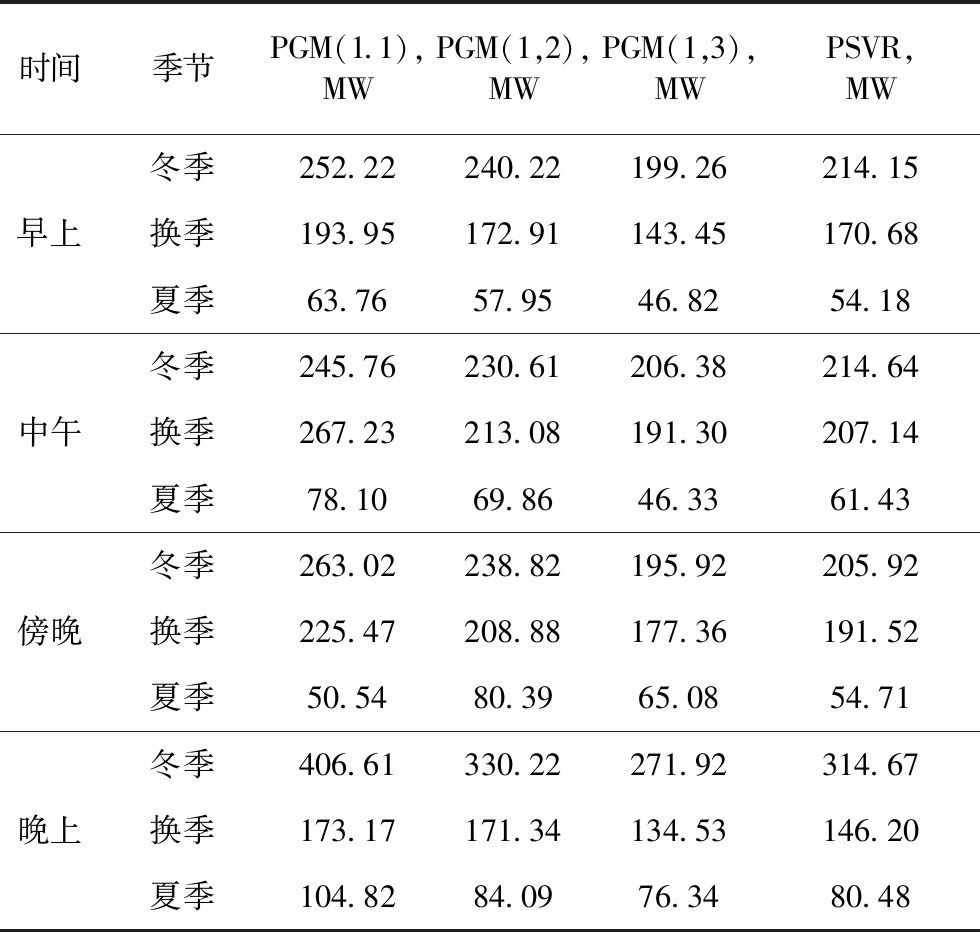
表2 初始净负荷预测MAE

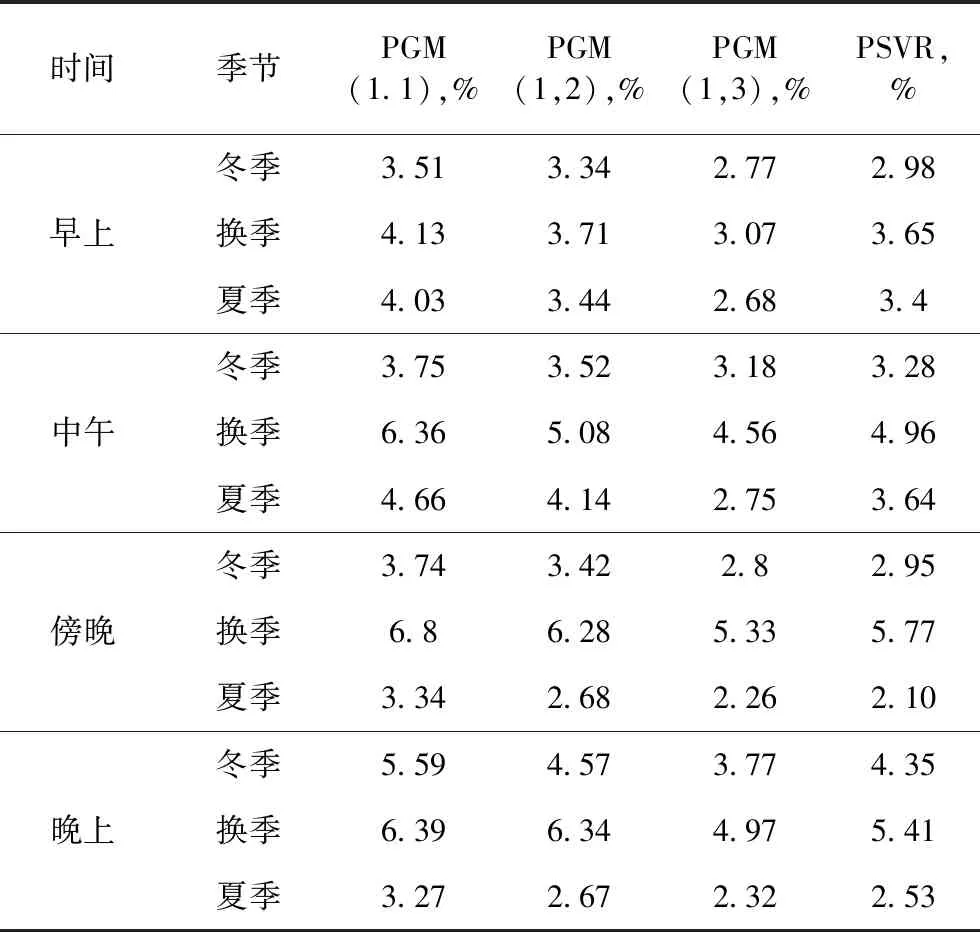
表3 初始净负荷预测MAPE

在以上三季中，夏季在初始NLF中的性能最好，这是由于夏季的天空通透度更好且拥有更好的基于其他相关性的可预测性能力。换季期间四个时间段内在最高MAE和MAPE中性能最差，如表2和3所示。和其他模型相比，PGM(1，3)模型在三季中体现出最佳性能。PGM(1，1)，PGM(1，2)，PGM(1，3)和PSVR模型的MAPE均值分别为4.63，4.15，3.4和3.76%。PGM(1，1)与PGM(1，3)相比，MAPE减小了36.17%。参考SVR模型与PGM(1，3)相比，MAPE减少了10.5%。图7为四个模型的绝对误差分布，结果表明PGM(1，3)性能最佳。高于虚线的数据点由加号符号表明，该虚线体现了不同模型的最大误差点。在四个模型当中，PGM(1，1)误差值最大为1 167.88 MW。

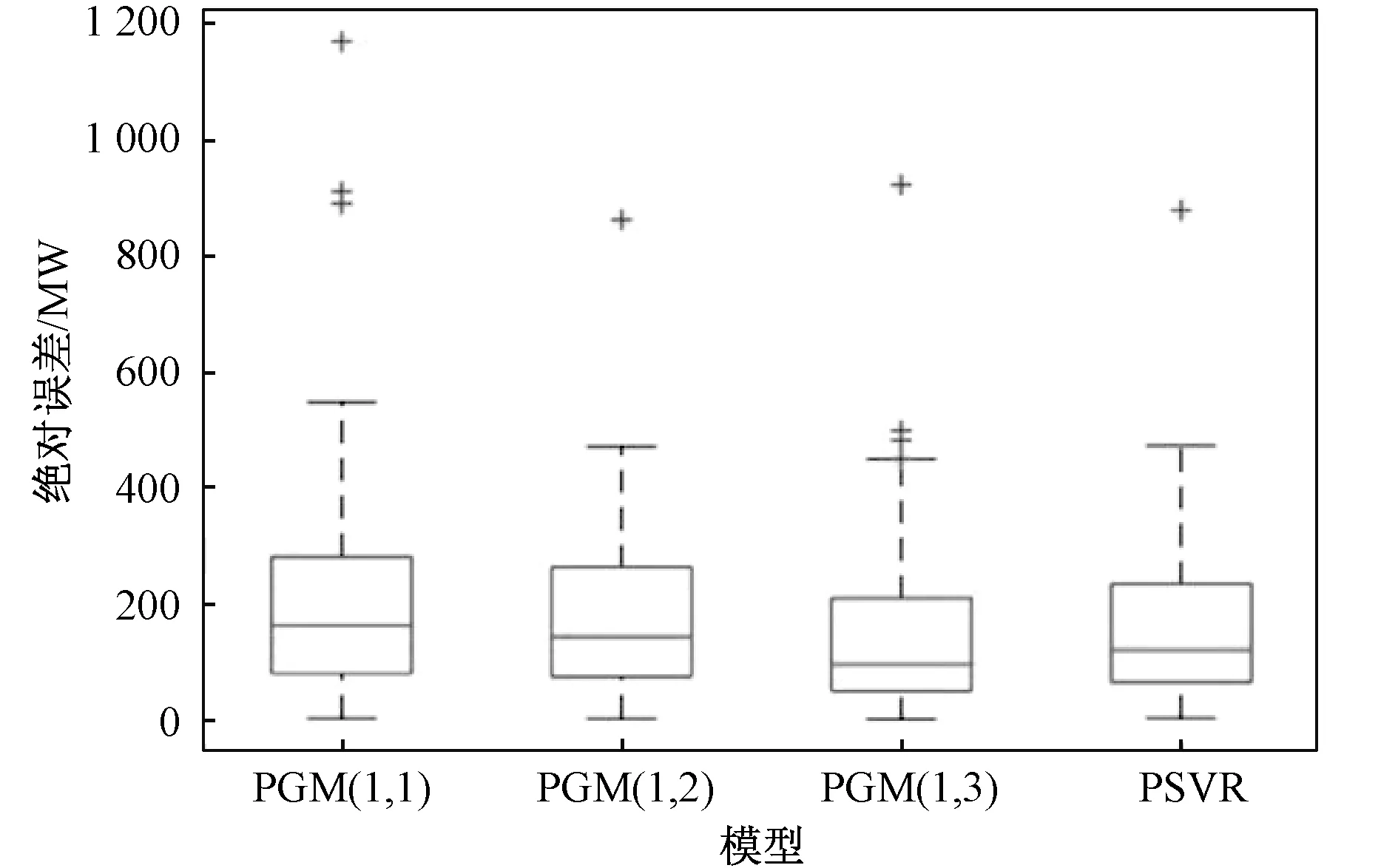
图7 初始预测总性能图 Fig.7 Overall performance of preliminary forecasting

3.3 不确定性估算

基于JPD的Gumbel copula模型可利用历史数据对负荷、太阳能和风能发电进行建立预测误差模型，且JPD样本可通过SAS根据研究需要求进行仿真。针对研究需求，SAS单时间步长下基于JPD仿真的Gumbel copula模型拟合总结和参数估算如图8所示。此类JPD样本用以估算NLF误差分布。在各时间步长下的上下不确定性可通过式(30)和(31)产生的NLF误差分布进行估算。

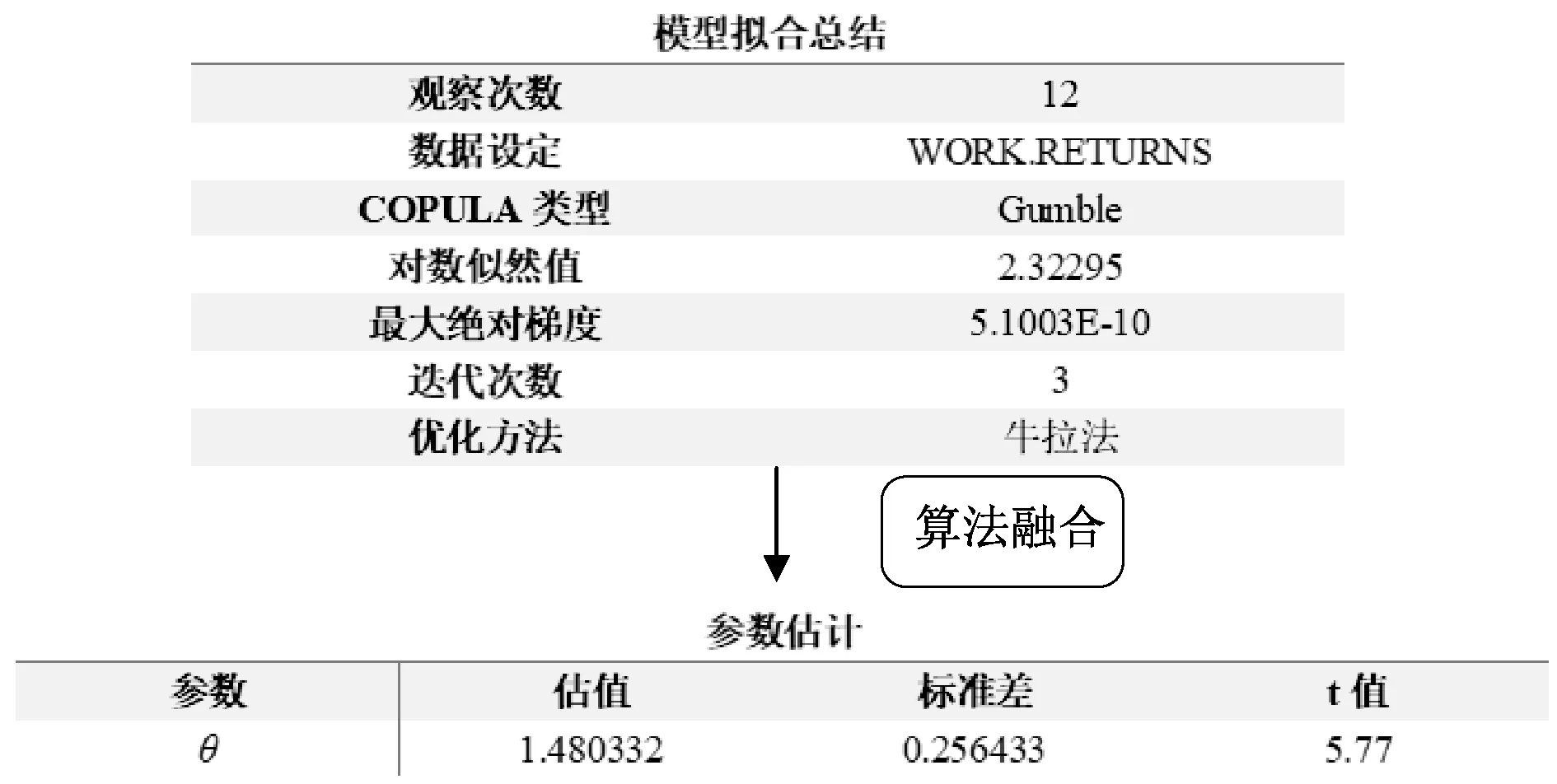
图8 单时间步长下基于JPD仿真的Gumbel copula模型拟合总结和参数估算图Fig.8 Model fit summary and parameter estimates of Gumbel copula based JPD simulation in SAS on demand for academics

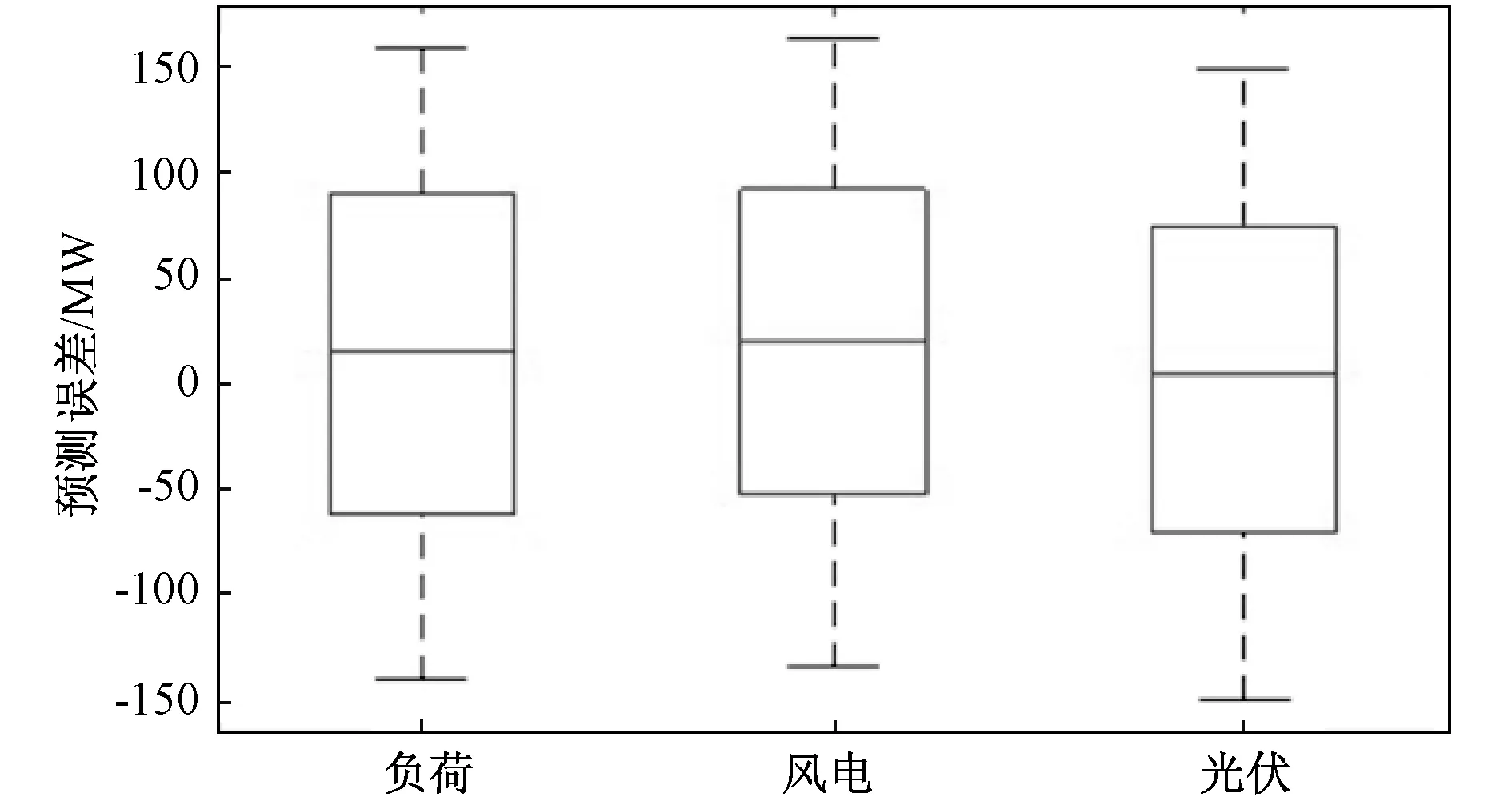
图9 联合分布箱型图Fig.9 Box of the joint distribution

在每个时间步长下的负荷、风能和太阳能预测误差的联合分布箱型图如图9所示。从图9可得负荷和风能预测误差主要分布在正向范围内，而太阳能预测误差几乎均匀分布。风能和负荷预测正误差可相互抵消。因此，在多数情况下，NLF误差将比负荷、风能和太阳能综合误差值更小。负荷和可再生能源预测误差的反向性导致了较高NLF误差。负荷误差正值和太阳能风能发电预测误差负值之差产生了正的NLF误差。该值与负荷、太阳能和风能发电预测误差的绝对值之和相等。NLF误差分布满足正态分布，如图10所示。

每个时间步长的向上和向下不确定性由式(30)和(31)估算得到。表4-6为早间(9.00 am -早10.00 am)，午间(午12.00 pm到午 1.00 pm)，傍晚(晚4.00 pm 到晚5.00 pm)及晚间(晚10.00 pm到晚 11.00 pm)不同季节下小时的不确定性。净负荷不确定性表明了净负荷波动可从预测的两个方向产生。和另外两个季节对比来看，换季时净负荷不确定性最高，这是由于换季期间有更多的不确定性气候特性。早间时刻的情况表明，向下不确定性高于向上不确定性，均值分别为115.63和107.80 MW。这是由于太阳能不规则向下斜坡抖动产生的。

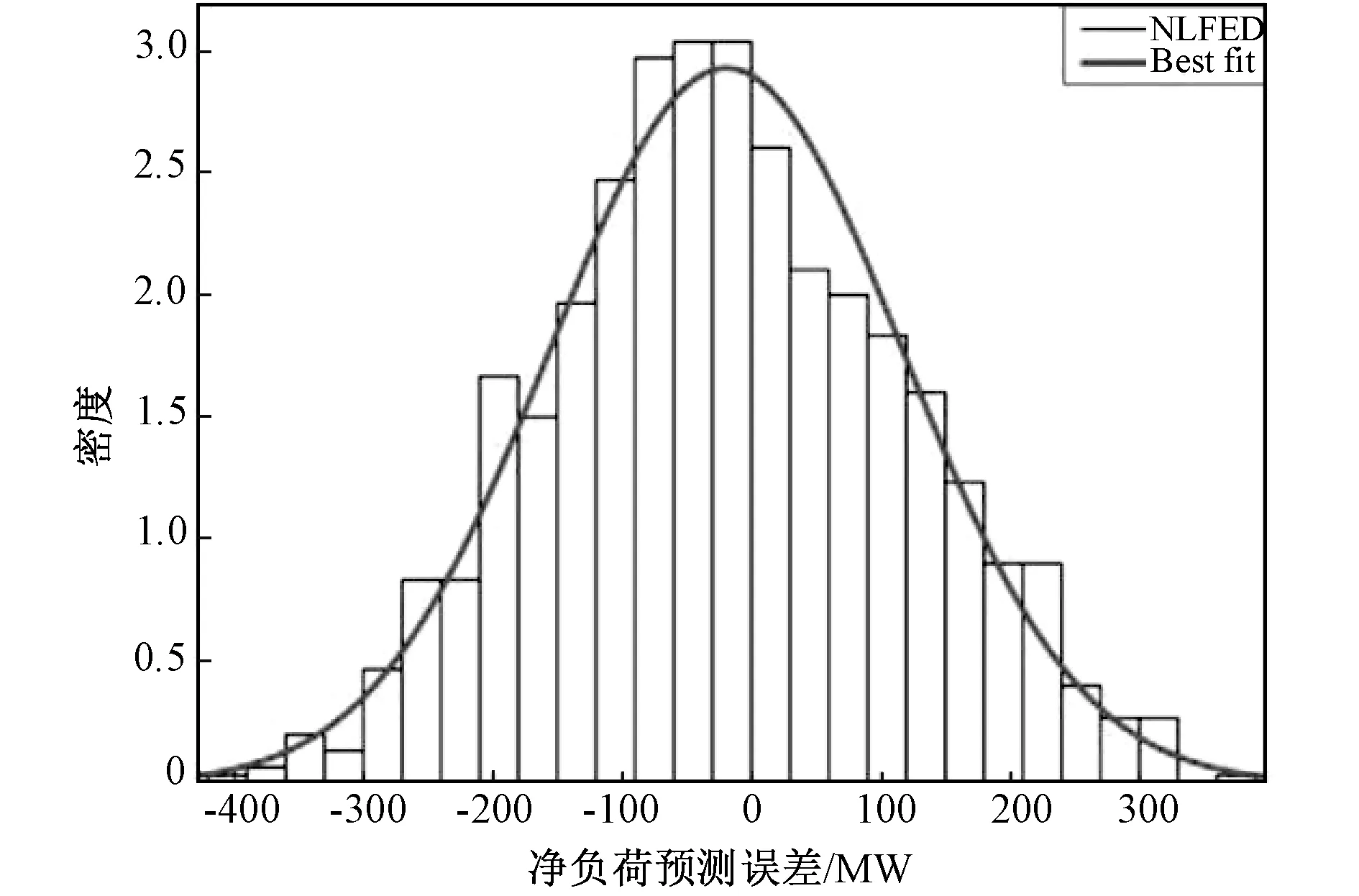
图10 NLF误差分布Fig.10 NLF error distribution

3.4 集合和直接NLF

在夏季早间小时时间范围下基于初始预测，预测间隔和联合预测的GM(1，3)如图11所示。结果表明大约99%的预测介于预测区间内，且预测曲线和初始预测相比更接近实际数据值。优化的集合净负荷预测如图12所示，可得MAPE对比图。鉴于PGM(1，3)在初始NLF中体现最佳性能，本文将对基于净预测值和初始经误差预测的GM(1，3)进行比较。PGM(1，3)表明其在冬季，换季和夏季的MAPE值分别为3.77，4.98 和2.46%。在冬季，换季和夏季期间，初始NLF比集合NLF的MAPE要分别减少37.09，5.06 和6.49%。

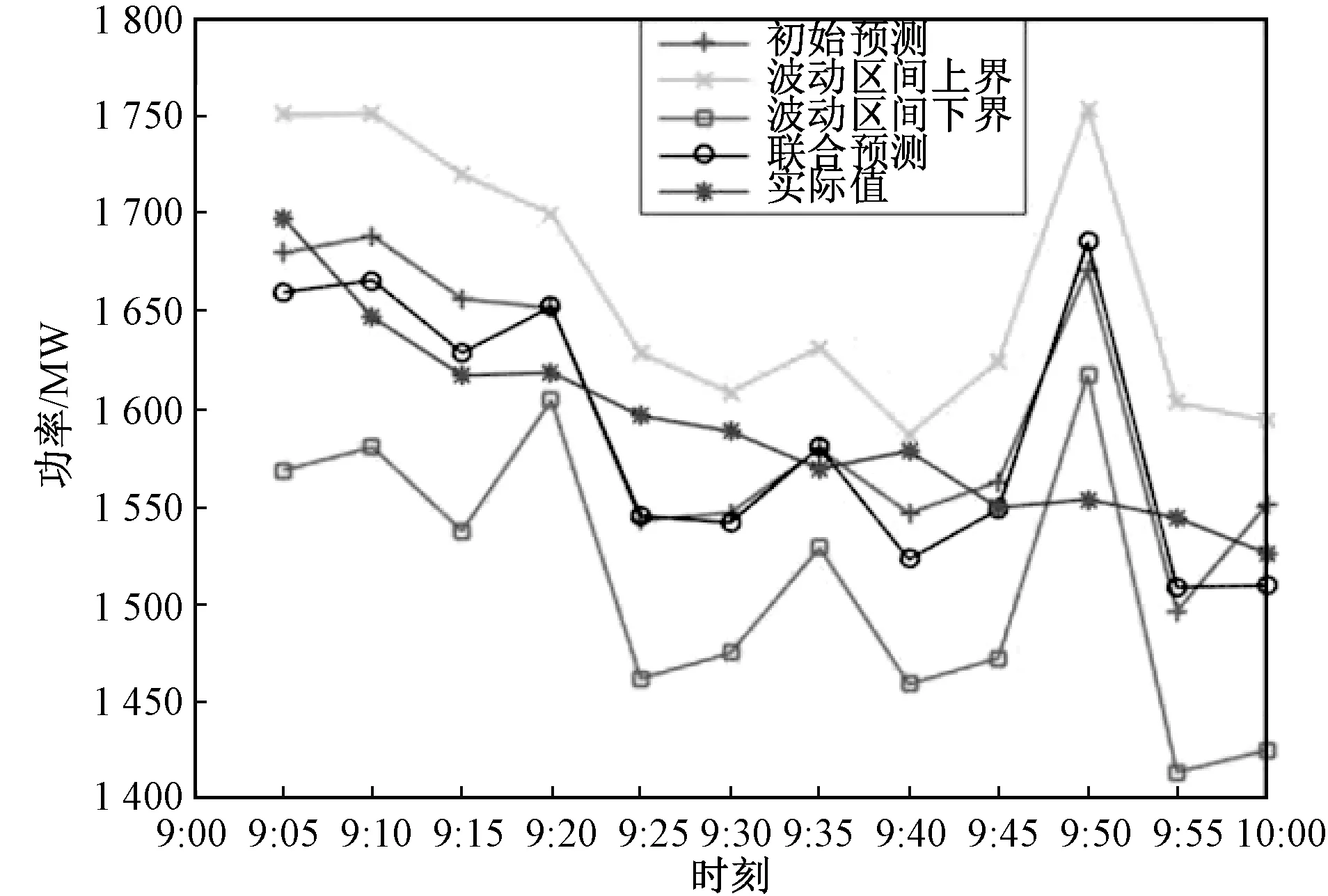
图11 性能曲线Fig.11 Performance plot

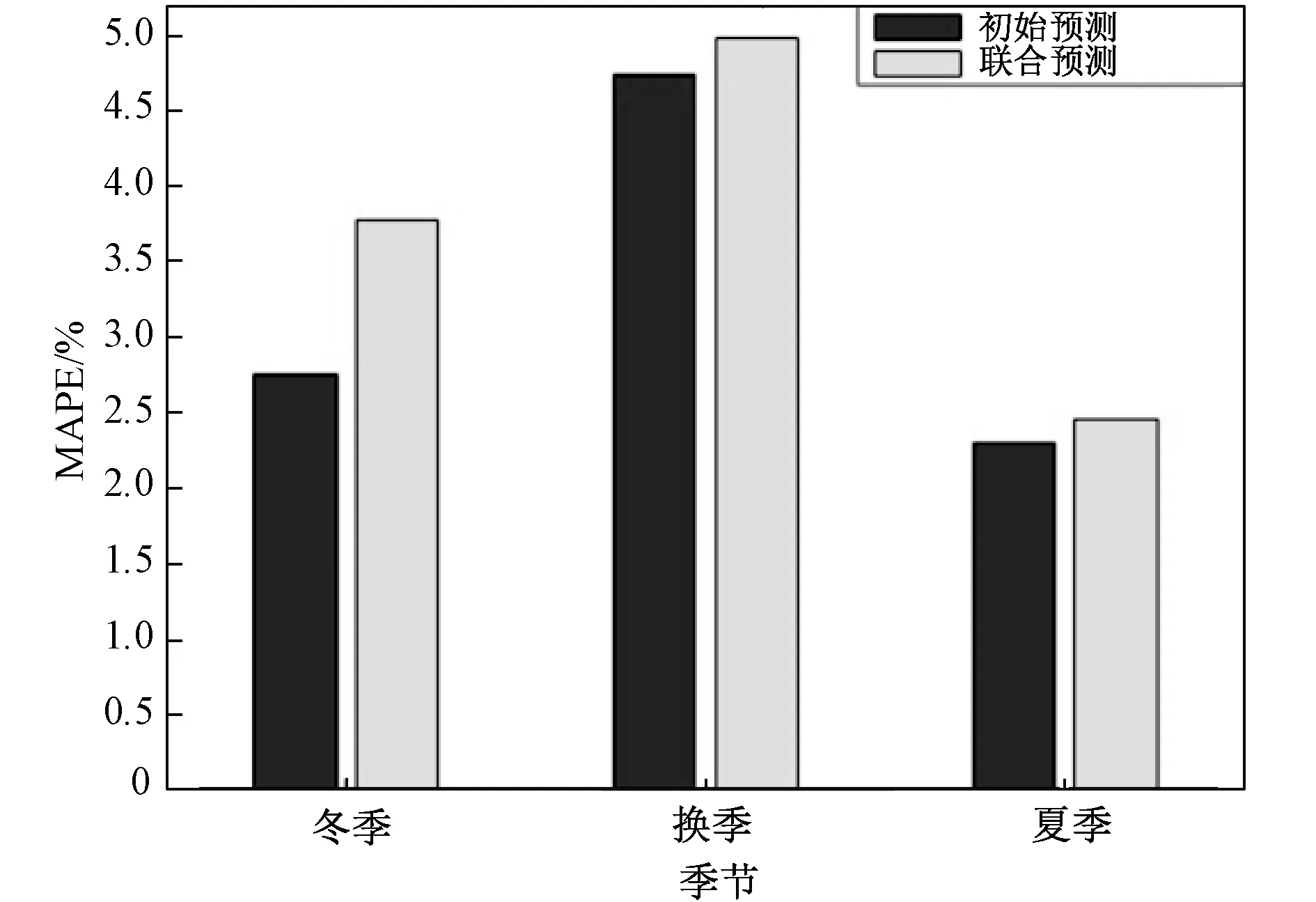
图12 初始和集合预测对比图Fig.12 Comparison between preliminary and aggregated forecasting

基于GM(1，3)的直接NLF方案中将采用历史净负荷时间序列和基于相关分析的外部输入。在不同季节下，基于所提集合预测，直接预测和SVR模型的集合预测MAE和MAPE分别如表7和表8所示。

和初始预测类似，夏季和换季期间将体现出最低和最高误差预测。在冬季GM(1，1)模型中，平均的MAE和MAPE分别为235.95 MW 和3.43%。在冬季，GM(1，1)模型与GM(1，2)模型相比，其MAE和MAPE将减少9.26 和8.20%；GM(1，1)和GM(1，3)模型相比，其MAE和MAPE将分别减少36.37 和23.82%。在冬季，GM(1，3)和SVR模型相比，其MAE 和 MAPE减少16.24 和 7.58%，因此其性能将优于参考SVR模型。换季期间GM(1，1)模型的MAE和MAPE值分别为214.12 MW和5.83%。换季期间，GM(1，1)比GM(1，2)的MAE和MAPE值分别要小10.42和7.16%，GM(1，1)比GM(1，3)模型的MAE和MAPE值分别要小13.19 和14.76%。在冬季，由于GM(1，3)的MAE 和 MAPE比参考SVR模型相应值减少13.19和 14.76%，因此其性能将优于参考SVR模型。

夏季的GM(1，1)模型的平均MAE和MAPE值分别为75.7和3.52%。GM(1，1)与GM(1，2)相比，其MAE和MAPE分别减少了43.91和7.64%。由于在夏季GM(1，3)模型的MAE和MAPE比SVR模型分别减少44.65和23.6%，因此GM(1，3)模型的性能优于SVR模型。图13给出了全年的所有模型的绝对误差分布。结果表明，离群值仅存在于GM(1，1)和直接NLF当中。所提NLF模型性能全年优于直接NLF模型，其MAE和MAPE值比直接NLF模型值分别减小47.77和33.88%。因此，所提模型可有效应用于短期NLF中。

为保证优化模型的性能，可采用ACF和PACF计算GM(1，3)模型的全年剩余相关性。剩余ACF和PACF分别如图14和15所示。由图可得，此时剩余量无相关性。因此，无剩余信息数据可进一步用于优化模型及其性能。

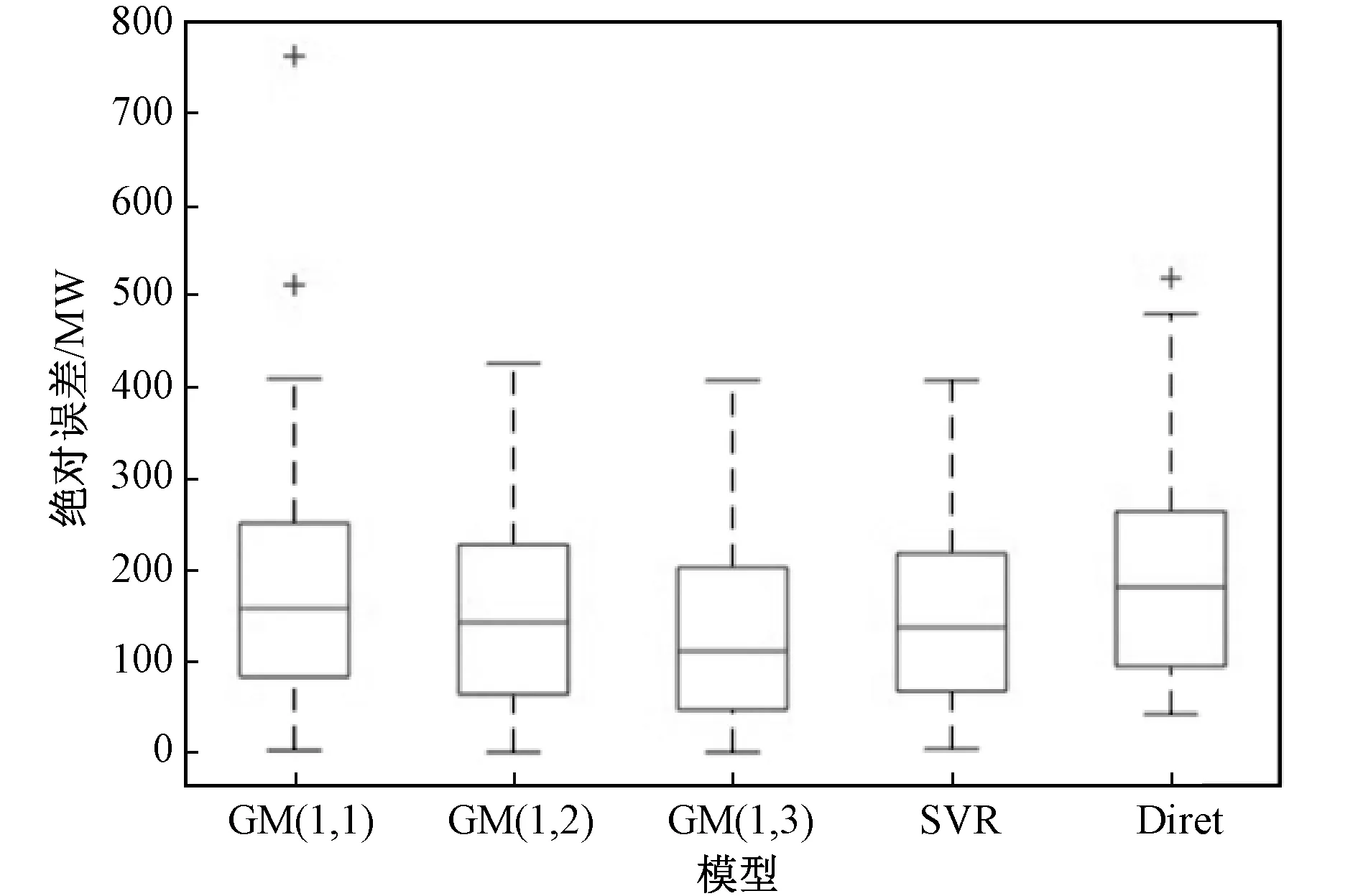
图13 集合和直接预测总性能图Fig.13 Overall performance of aggregated and direct forecasting

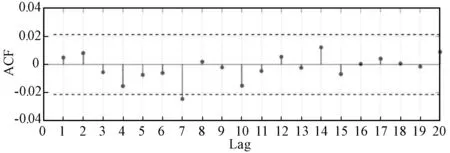
图14 GM(1，3)模型剩余值ACF图 Fig.14 ACF plot of GM (1, 3) model residues

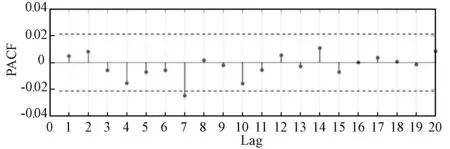
图15 GM(1，3)模型剩余值PACF图Fig.15 PACF plot of GM (1, 3) model residues

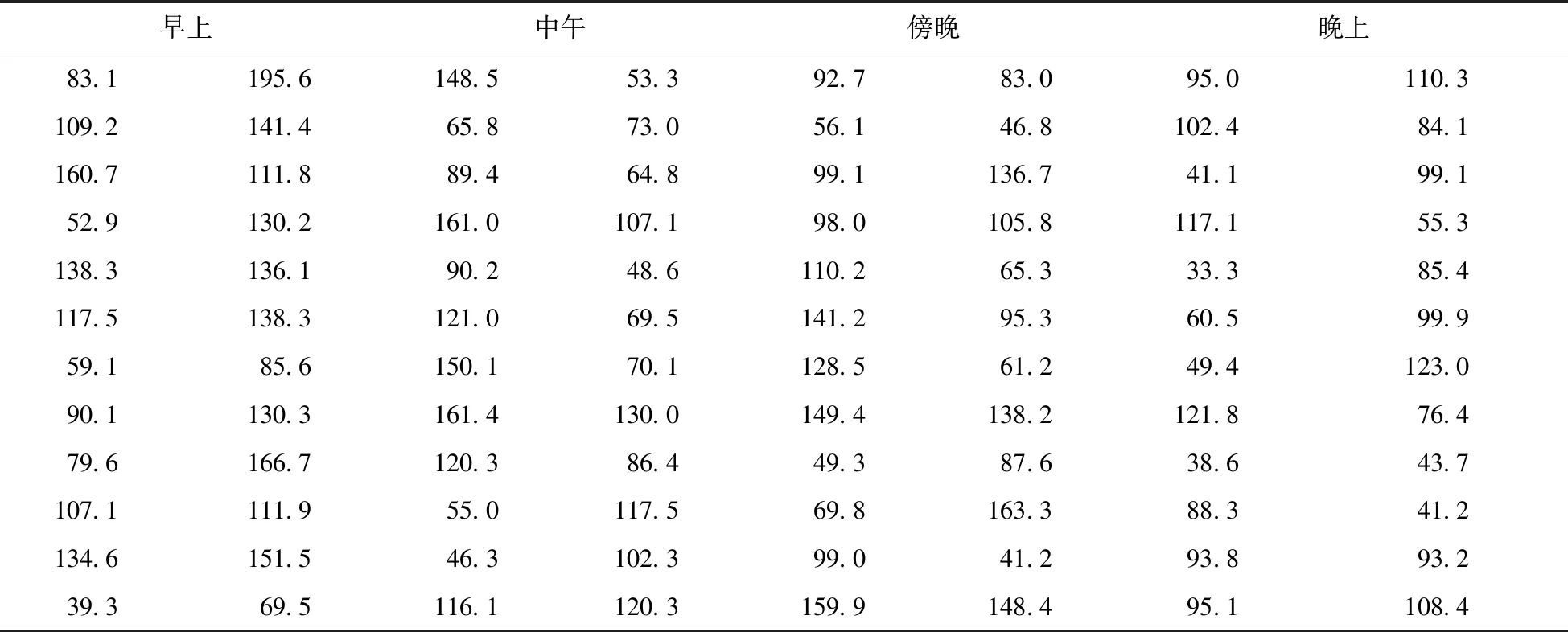
表4 冬季不确定值上下边界

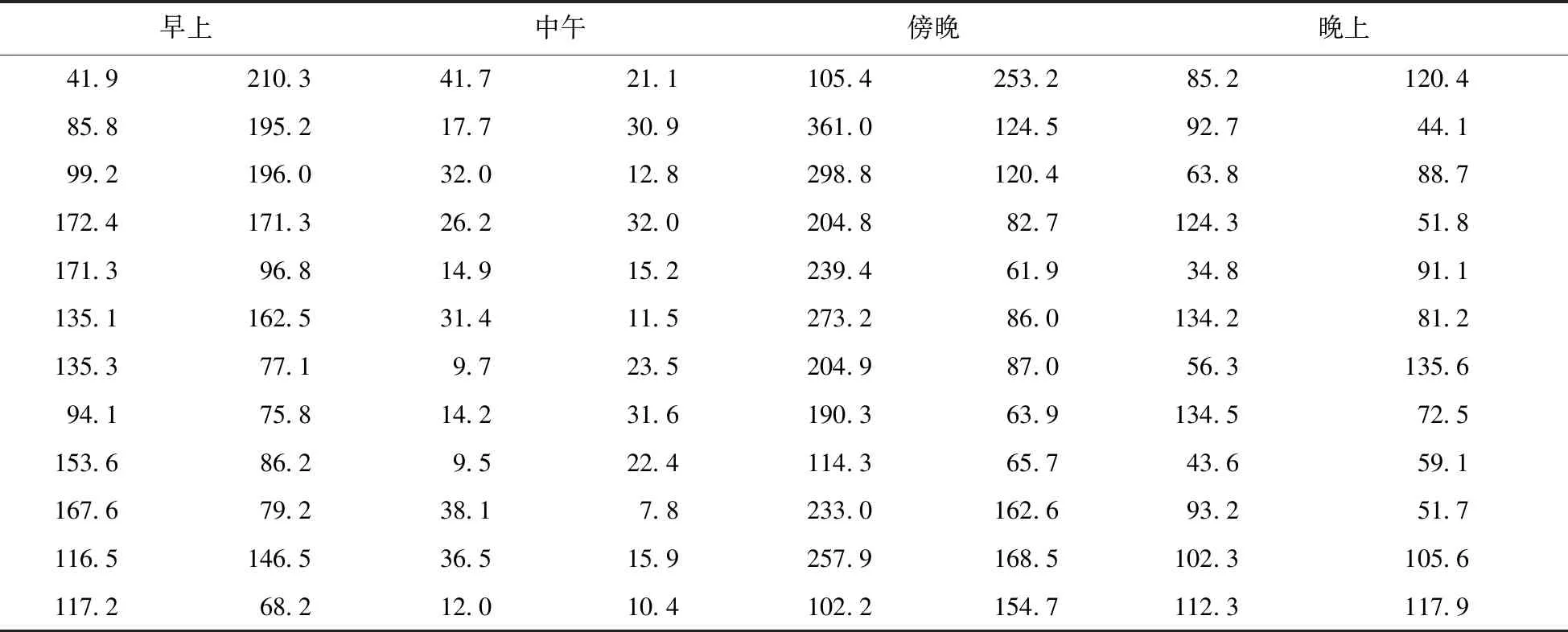
表5 换季期间不确定值上下边界

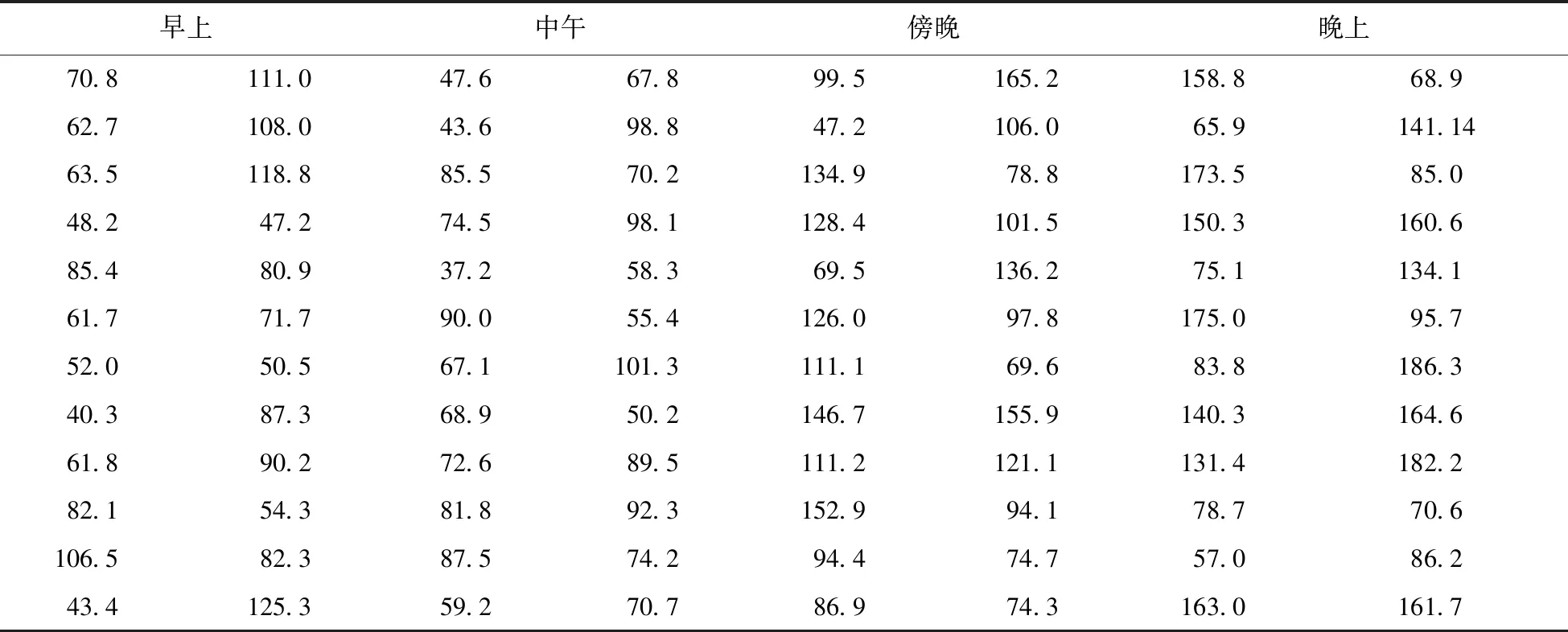
表6 夏季不确定值上下边界

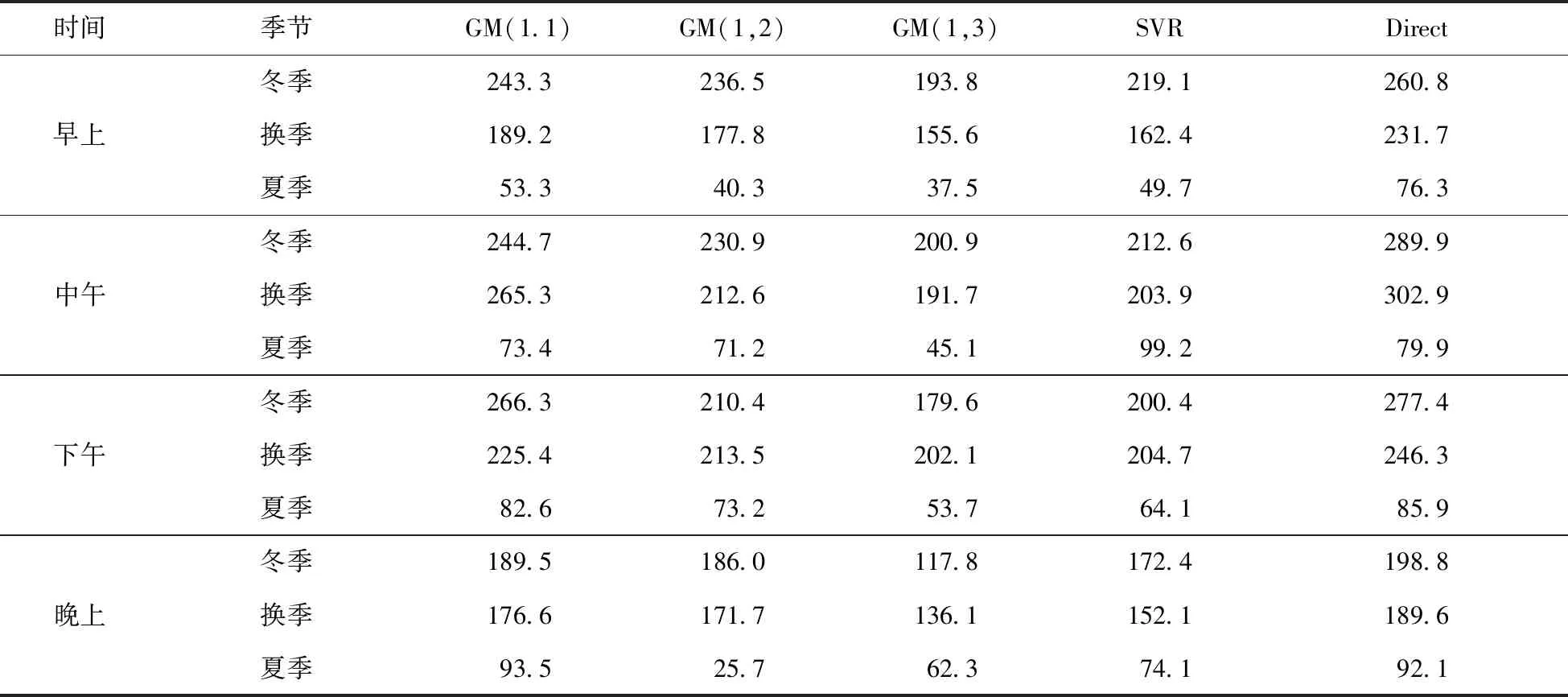
表7 集合净负荷预测MAE值

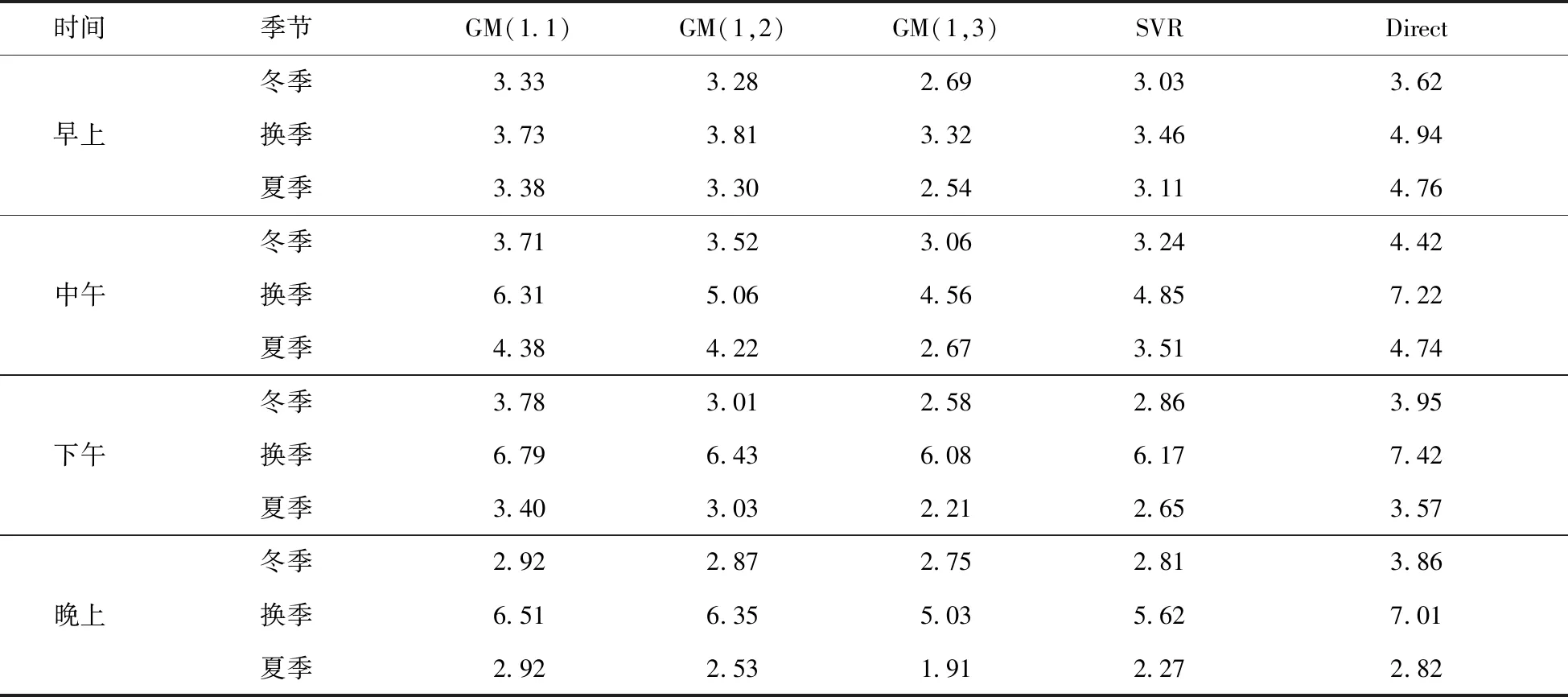
表8 集合净负荷预测MAPE值

4 结 论

现代电力系统中，为实现传统发电机组优化调度规划，系统要求净负荷可进行精确预测，从而支撑大规模可再生能源并入。因此本文提出一种新型短期NLF模型。鉴于有限输入条件和运行时间要求，所提模型采用修正Grey指数模型对单个负荷和可再生能源发电预测进行估算。三种Grey指数模型和外部参数基于相关性分析获得，初始预测则通过基于负荷和可再生能源预测误差的Gumbel copula联合概率分布的净负荷不确定性集合来增加预测准确率。所提模型包含区间预测和联合中心预测。结果表明所提基于GM(1，3)的模型性能优于初始模型、SVR模型以及直接NLF模型。