电站空冷散热器动态传热特性研究
2020-04-10闫景波杨立军
闫景波, 杨立军
(华北电力大学 能源动力与机械工程学院, 北京 102206)
0 引 言
翅片管换热器已被广泛应用于间接空冷发电厂的冷端系统,是间接空冷系统的重要组成部分。间接空冷系统以环境空气为冷却介质,空气流过翅片管束表面,带走管束内循环水的热量,使得换热器中的循环水得到冷却[1]。目前关于电厂空冷散热器的研究多为稳态特性研究[2,3,4]。然而在实际运行过程中,由于环境条件、电厂负荷、运行工况等经常发生变化,翅片管换热器的工作条件也会经常发生改变,因此需要对空冷散热器的动态特性展开研究。
目前已有大量关于换热器动态特性的研究成果。梁新宇等[5]建立了螺旋式换热器近分相流动态模型,并将模拟结果和实验数据进行了对比。Gartner[6]等通过实验方法研究了翅片换热器的动态特性,此外建立了换热器的数值模型,研究了流体入口温度以及流量变化时换热器的动态响应特性。Dusinberre等[7]研究了气-气交叉流换热器的动态特性,采用有限差分法对能量方程进行了求解。Pearson等[8]建立的换热器动态模型中考虑了换热管径向和轴向的热传导,研究了热流体入口温度发生阶跃、斜坡和指数变化时换热器的瞬态响应特性。Roetze等[9]假定换热系数不随流量变化,研究了换热器流量阶跃变化时的动态变化过程。Mishra等[10]研究了流体温度和流量扰动时换热器的动态响应,对热流体入口温度和冷热流体流量同时变化的工况进行了分析。Gao等[11]分析了换热器流体入口温度和流量随时间变化的瞬态响应,对热流体入口温度和冷、热流体质量流量的变化组合情况进行了建模和分析。
虽然关于换热器动态特性的研究很多,但是不同换热器结构形式、尺寸、工质种类以及运行参数等相差较大,因此有必要对应用于火电厂间接空冷系统的空冷散热器的动态特性展开针对性研究。此外,上述文献在对换热器动态过程进行数值模拟时,一般假定初始时刻冷热流体不同位置温度相同,这与实际工况并不符合。本研究针对初始时刻冷热流体的温度分布并不均匀,温度分布和实际工况一致的工况,研究了冷却空气迎面风速、循环水质量流量和入口温度发生阶跃变化时空冷散热器的动态响应特性,分析了上述变量变化程度对换热器动态响应过程的影响。
1 数学模型
间接空冷系统的翅片管换热器结构如图1所示。冷却空气流过翅片管束,带走循环水的热量。本文采用的数学模型与文献[10,11,12]一样,并有以下假设:
(1)入口空气的速度和温度沿竖直和水平方向的分布是均匀的;
(2)忽略了冷热流体和金属管壁沿周向和轴向的导热;
(3)由于换热器沿空气流动方向的长度较短,因此不考虑空气沿流动方向的温度分布,只考虑空气进出口温度的变化;
(4)忽略流动过程中的粘性耗散;
(5)工质的物性参数不随时间变化。
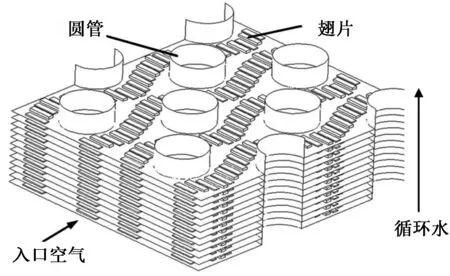
图1 空冷散热器用翅片管束Fig.1 Finned tube bundles of air-cooled heat exchanger
1.1 控制方程
根据以上假设,循环水侧、管壁和空气侧的非稳态换热偏微分方程如下所示。
循环水侧控制方程:
(1)
式中:x为空间变量,m;τ为时间变量,s;cp,w为水的比热容,J/(kg·K);mw为控制体内水质量,kg;Mw为水的质量流量,kg/s;L为管束长度,m;hw为水侧对流换热系数,W/(m2×K);Aw为水侧换热面积,m2;Tw和Twall分别为水和管壁温度,K。
管壁控制方程:
(2)
式中:cp,wall为管壁金属的比热容,J/(kg·K);mwall为管壁金属质量,kg;ha为空气侧对流换热系数,W/(m2·K);Aa为空气侧换热面积,m2;Ta1和Ta2分别为空气入口和出口温度,K。
空气侧控制方程:
haAa×(Twall-(Ta1+Ta2)/2)
(3)
式中:cp,a为空气的比热容,J/(kg·K);ma为控制体内空气质量,kg;Ma为空气的质量流量,kg/s。
1.2 初始和边界条件
在初始时刻,已知入口水温和入口空气温度时,循环水沿管长方向的温度分布以及出口空气温度可由方程(1)~(3)联立求解。本文选定的标准状况下空气迎面风速为4 m/s,空气入口温度为289.15 K。循环水质量流量为45 kg/s,循环水入口温度为323.15 K。
本文分别研究了空气质量流量、循环水质量流量、循环水入口水温发生扰动变化时,换热器的动态响应过程。本文变量的扰动变化为阶跃变化,即从初始时刻由一个值瞬间变为另外一个值。
1.3 模型求解和验证
换热平衡方程的时间项和空间项分别采用向前差分格式和一阶迎风格式进行离散,采用改进欧拉法对离散后的方程求解,使用MATLAB软件对离散后模型进行了求解计算[13]。本文进行了时间步长和空间长度的敏感性分析,最终选定的时间步长为0.001 s,沿水流动方向划分为50个网格。
为了验证模型的准确性,将使用本模型计算所得的模拟结果和文献[14]的实验结果进行了对比,数值模拟所用翅片管束的结构参数和实验所用相同,模拟结果和实验结果的对比如图2所示。可以看出,模拟值和实验值在不同风速下相差不大,说明该模型可以准确的模拟换热器的动态响应过程。
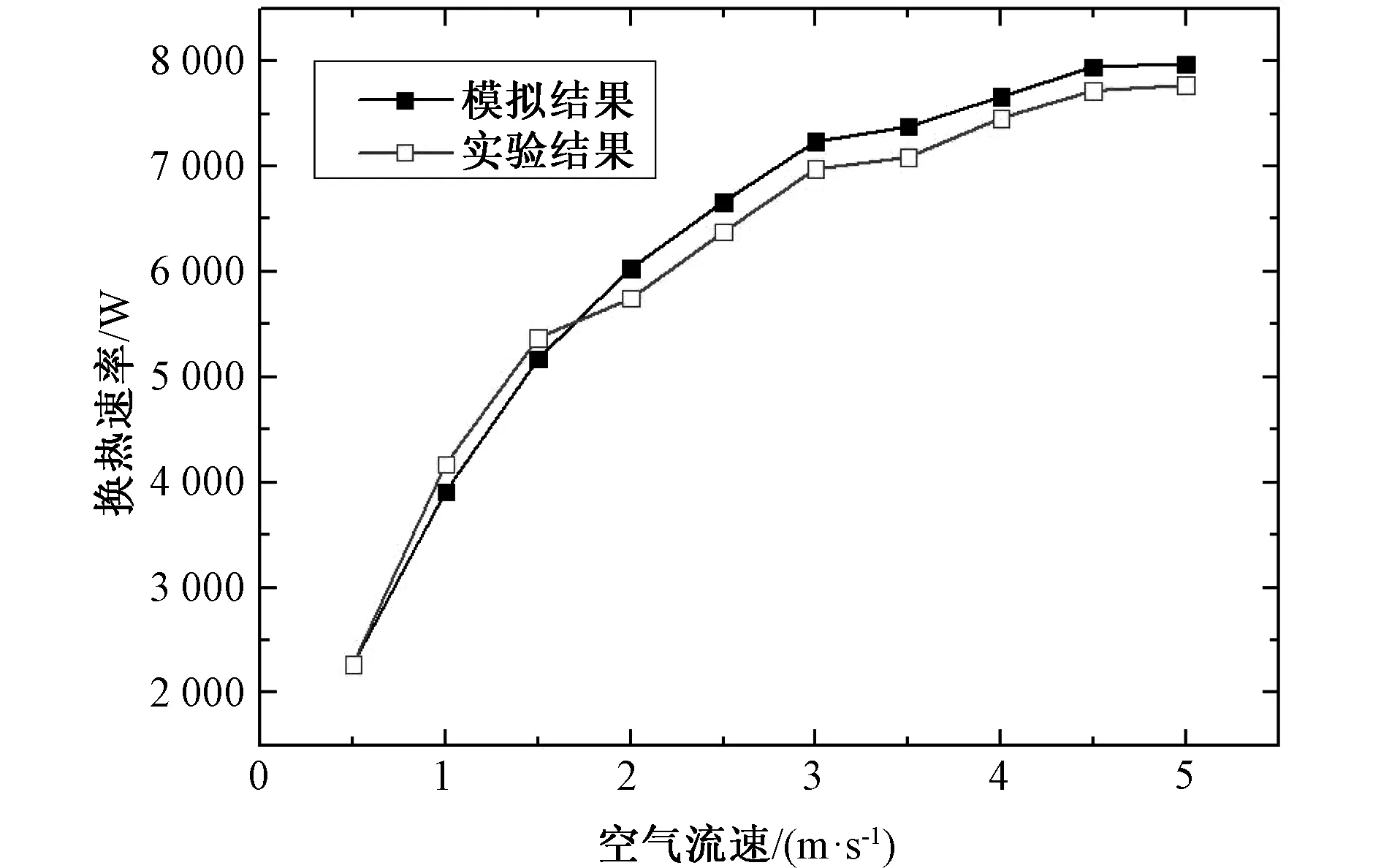
图2 模型验证Fig.2 Model validation
2 结果和讨论
本文研究了迎面风速、循环水质量流量和入口温度发生变化时,换热器的动态响应过程。分析了扰动变量的变化程度对换热器动态特性的影响。
2.1 迎面风速变化
本节研究了换热器迎面风速变化程度不同时换热器的动态响应特性。采用响应时间τre来反映扰动产生后换热器从一个稳态到另一个稳态所需要的时间,响应时间τre定义为空气出口温度或循环水出口温度的变化程度达到整个变化程度的90%所需的时间。
图3(a)、(b)分别为换热器迎面风速产生阶跃变化后,空气出口温度、循环水出口温度随时间变化的曲线。从图中可以看出,迎面风速变化程度越大,对应的动态曲线变化幅度也越大。空气质量流量增加时,空气和循环水的出口温度均会降低。这是由于当空气质量流量增加时,空气侧的换热系数增大,总的换热量增加,因而循环水出口水温随之降低。对于空气侧,由于单位时间内带走一定热量的空气量大大增加,因此出口空气温度也会显著降低。空气质量流量减少时,趋势则相反。此外,空气流量阶跃变化后,空气出口温度会在极短时间内大幅变化至一定值,随后变化幅度相对缓慢。循环水出口温度在动态响应初始阶段不会大幅度变化。以空气迎面风速增加为例,产生这种现象的原因可解释如下。
方程(1)、(2)、(3)可以分别写成如下离散形式:
hwAw(Twall-Tw))+Tw
(4)
Twall′=hwAw(Tw-Twall)+
haAa(Ta-Twall)+Twall
(5)
haAa(Twall-Ta))+Ta
(6)
式中:Tw′、Twall′和Ta′分别表示下一时刻控制体内水、管壁和空气的平均温度,K;Tw1和Tw2分别表示控制体的进出口水温,K。从式中可以看出,对于空气侧和水侧,动态响应快慢主要由工质热容量(ma(w)cp,a(w))、工质质量流量(Ma(w))、对流换热热阻(1/ha(w)Aa(w))和换热温差|Twall-Ta(w)|决定。工质热容量越大,动态响应速度越慢。由于空气密度远远小于金属管壁和水的密度,其热容量也远远小于后两者。当空气侧体积和密度不变时,空气质量流量大小取决于迎面风速,空气迎面风速突然增加时,由于空气热容量较小,方程(10)的cp,aMa(Ta1-Ta2)项在初始时刻会迅速降低,而haAa(Twall-Ta)项则变化缓慢,使得初始时刻空气出口温度迅速降低。当空气出口温度降低至一定值时,cp,aMa(Ta1-Ta2)和cp,aMa(Ta1-Ta2)会比较接近,此时出口空气温度的变化和管壁温度以及水温的变化密切相关。而管壁和循环水的热容量较大,其动态响应速度相对较慢,空气侧的动态响应速度也随之变慢。
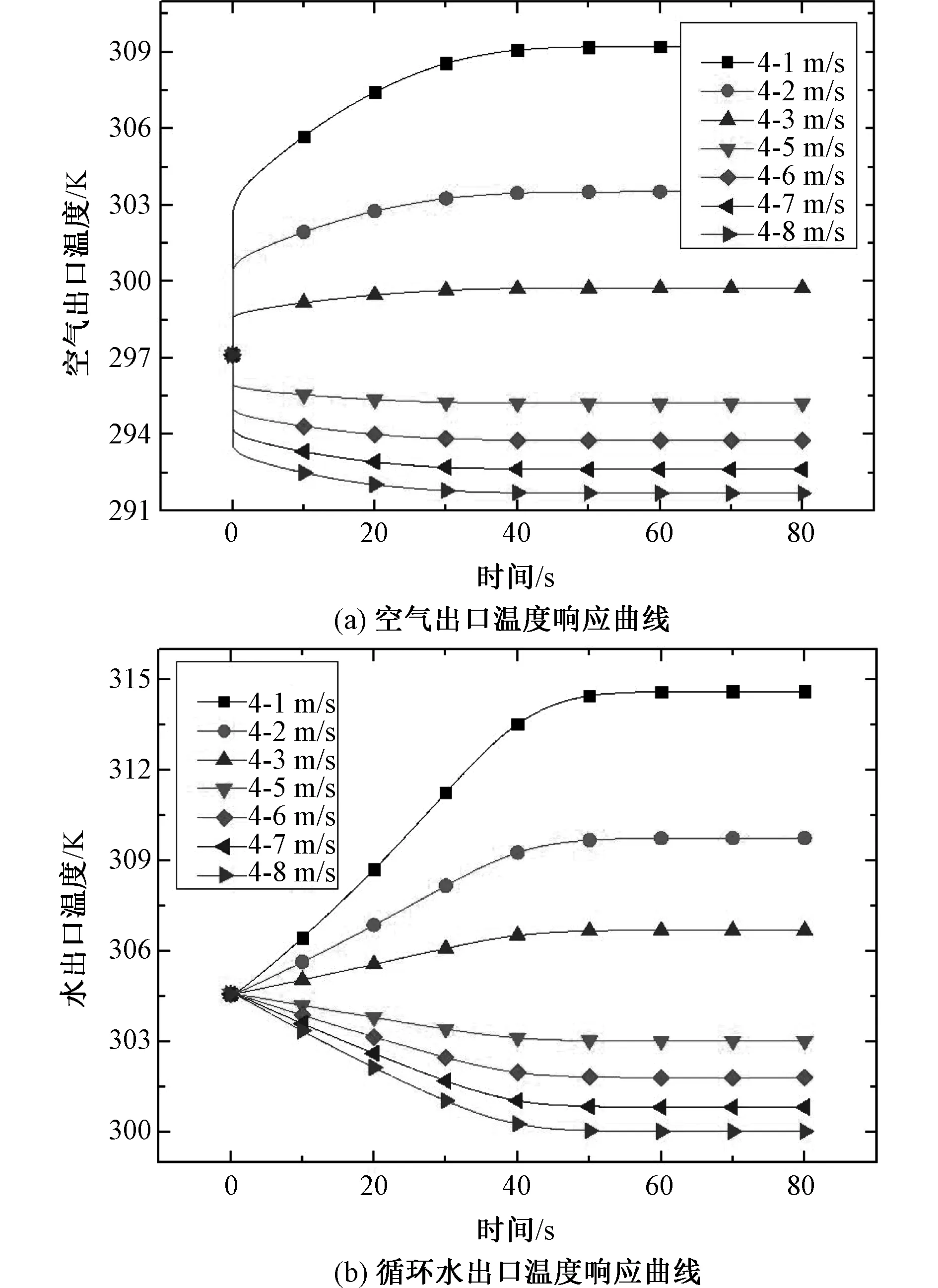
图3 迎面风速变化时的动态响应曲线 Fig.3 Response curve with air face velocity variation
图4为出口空气流量阶跃变化时的动态响应时间,从图中可以看出,循环水出口温度的响应时间要明显长于空气出口温度的响应时间。这是由于动态过程开始后的初始阶段,出口空气温度迅速增加造成的。此外,空气迎面风速的最终值越大,所需的响应时间会更短。这是由于更高的风速也意味着更大的质量流量,这会使得空气侧动态响应加快;此外,更高的风速也会使得空气侧换热系数增大,导致空气侧和管壁侧动态响应均变快。而空气和管壁动态响应加快时,会造成更大的换热温差,也会加快水侧的动态响应过程。
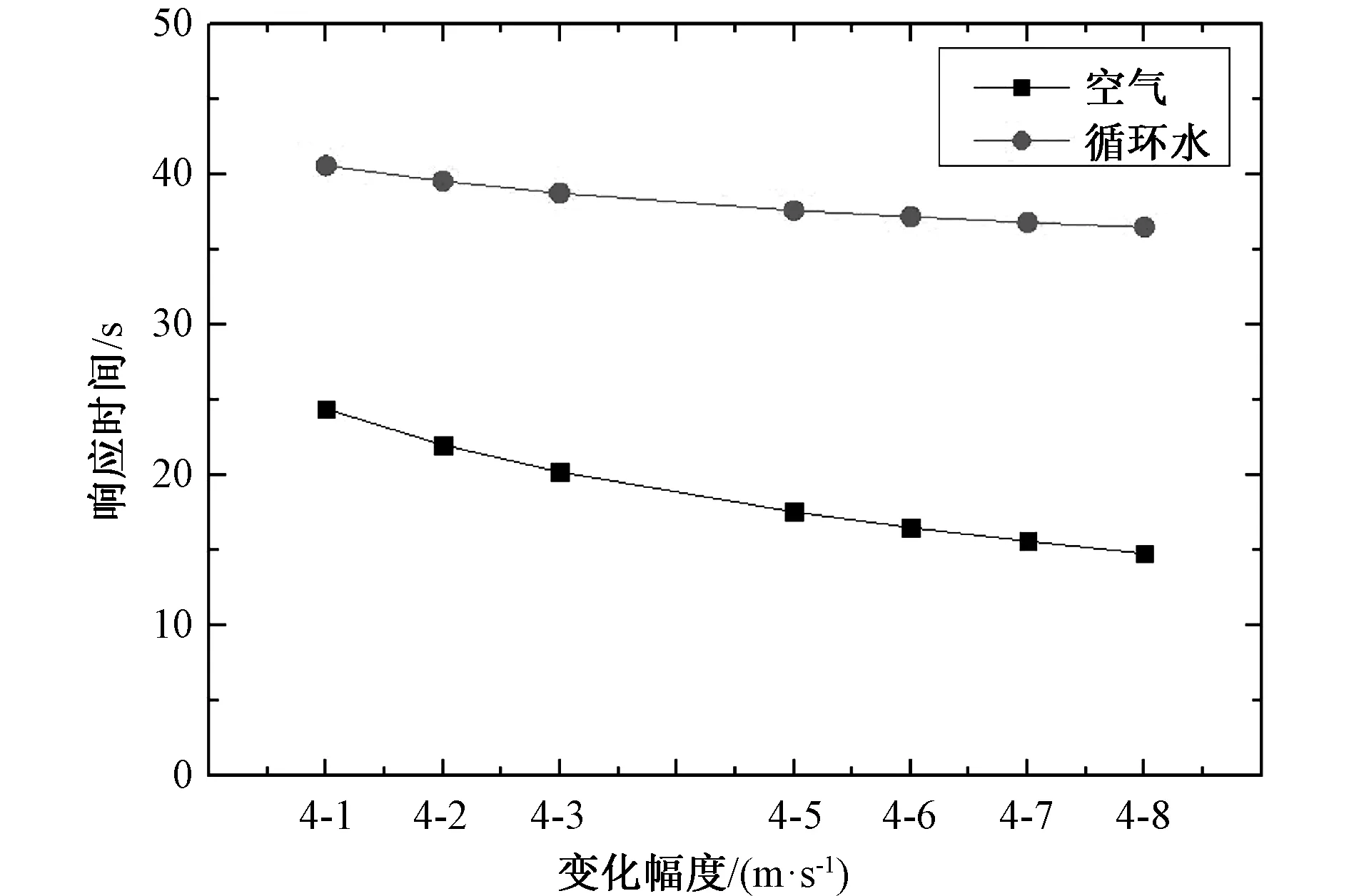
图4 迎面风速变化时的响应时间 Fig.4 Response time with air face velocity variation
2.2 循环水流量变化
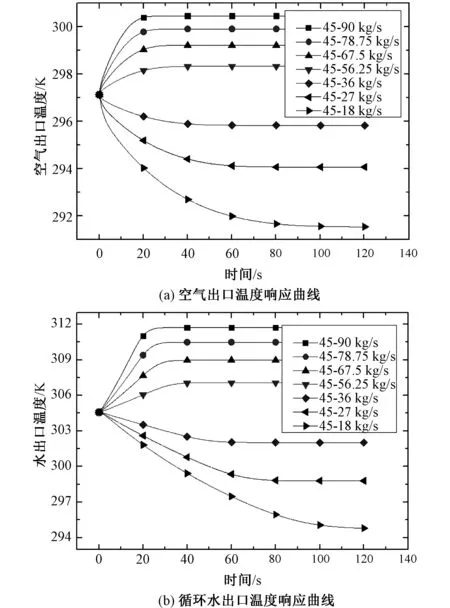
图5 循环水流量变化时的动态响应曲线 Fig.5 Response curve with water mass flow rate variation
图5为循环水流量阶跃变化时空气和循环水出口温度的动态响应曲线。从图中可以看出,循环水流量变化程度越大,对应的动态曲线变化幅度也越大。当循环水量增加时,最终稳态时空气和循环水出口温度均会增加。循环水量增加幅度越大,出口温度增加幅度也随之变大。当循环水流量增加时,由于空气侧空气流速和换热系数不变,空气侧冷却能力不变,相同时间内空气需要冷却更多质量流量的循环水,最终会造成循环水出口水温的增加。而出口水温的增加,也会使得空气侧换热温差变大,换热量增加,最终造成出口空气温度也增加。当循环水量减少时,空气和循环水出口温度的变化趋势则相反。从图6可以看出,循环水质量流量越大,空气侧和循环水侧的响应时间越小。对于较高的循环水质量流量,扰动发生后,水侧上游部分高温区域向下扩散速度加快,这会加快水侧整体的温升速率。此外,更高的循环水质量流量也会使得水侧换热系数增大,从而使得水侧响应时间变短。而水侧动态响应速度变快后,会造成管壁和空气侧温差变化速率加快,最终使得空气侧响应时间变短。
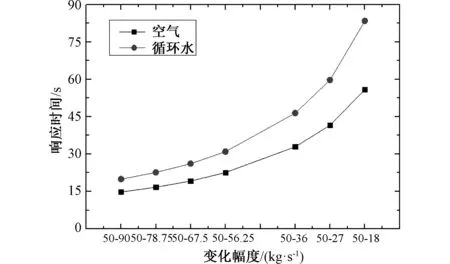
图6 循环水流量变化时的响应时间 Fig.6 Response time with water mass flow rate variation
2.3 循环水入口温度变化
图7为循环水入口温度阶跃变化时空气和循环水出口温度的动态响应曲线。从图中可以看出,入口水温变化程度越大,动态响应曲线的变化幅度也越大。循环水入口温度增大时,循环水和空气的出口温度均会随之增大。这是由于当循环水入口温度增大时,对于水侧,由于入口水温增加,上游高温水会逐渐向下游流动,从而使得水侧整体水温逐渐上升。而水侧和空气侧换热系数和流量不变,此时换热温差增大,会使得空气侧换热量增大,空气出口温度随之增加,使得空气侧换热能力增加。随着动态过程进行,水侧和空气侧整体温度会升至一定值,最终达到热平衡状态。循环水入口温度降低时,循环水和空气的出口温度变化趋势相反。从图7(b)可以看出,循环水入口温度阶跃变化后,在动态响应开始的一段时间内,水侧出口水温没有变化。这是由于高温入口水流动到出口位置需要一定时间,在到达出口位置前出口水温并不会产生变化。从图8可以看出,水侧质量流量阶跃变化时,其变化幅度的大小对于动态过程响应时间没有影响。
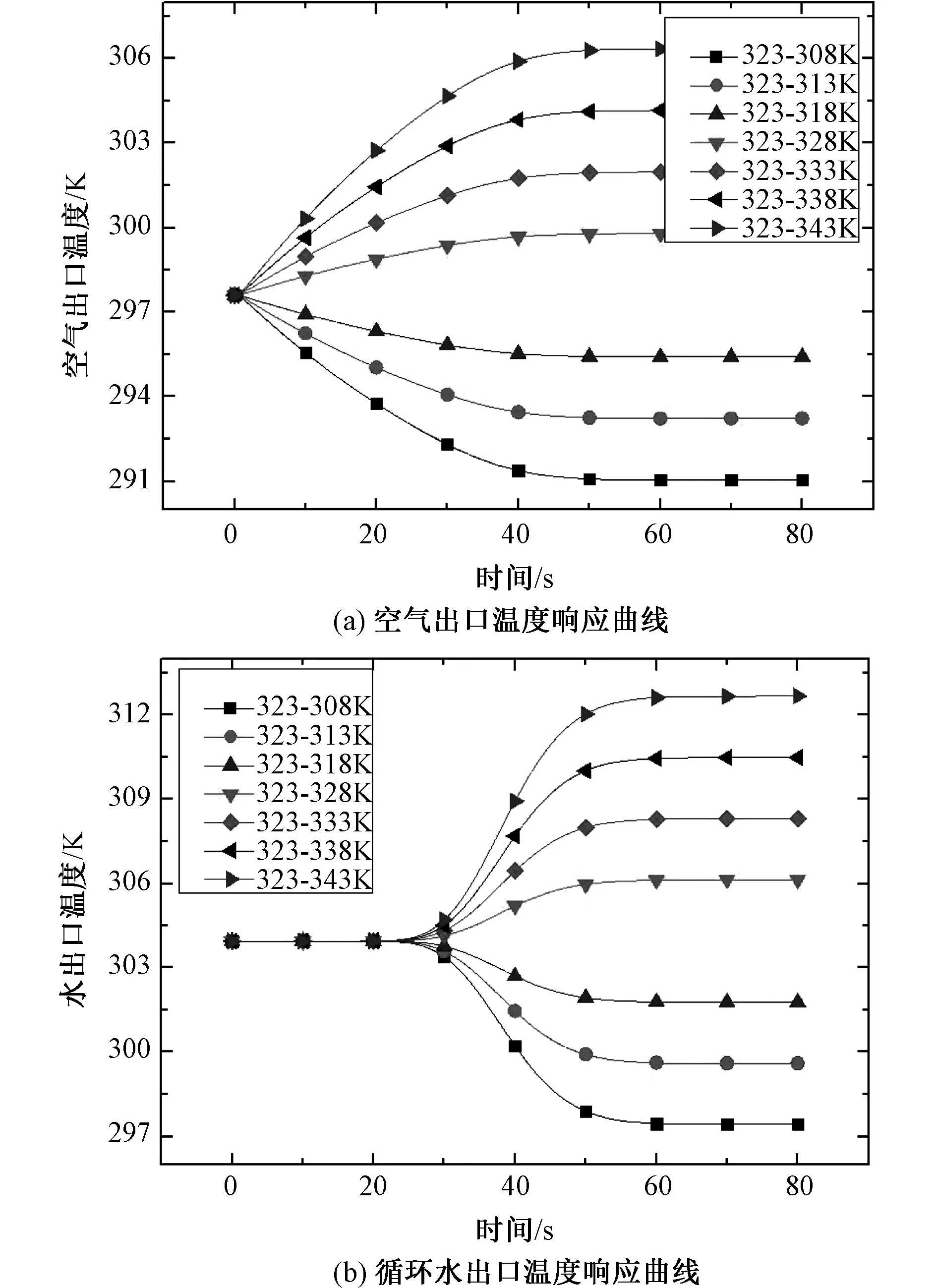
图7 循环水入口温度变化时的动态响应曲线Fig.7 Response curve with water inlet temperature variation
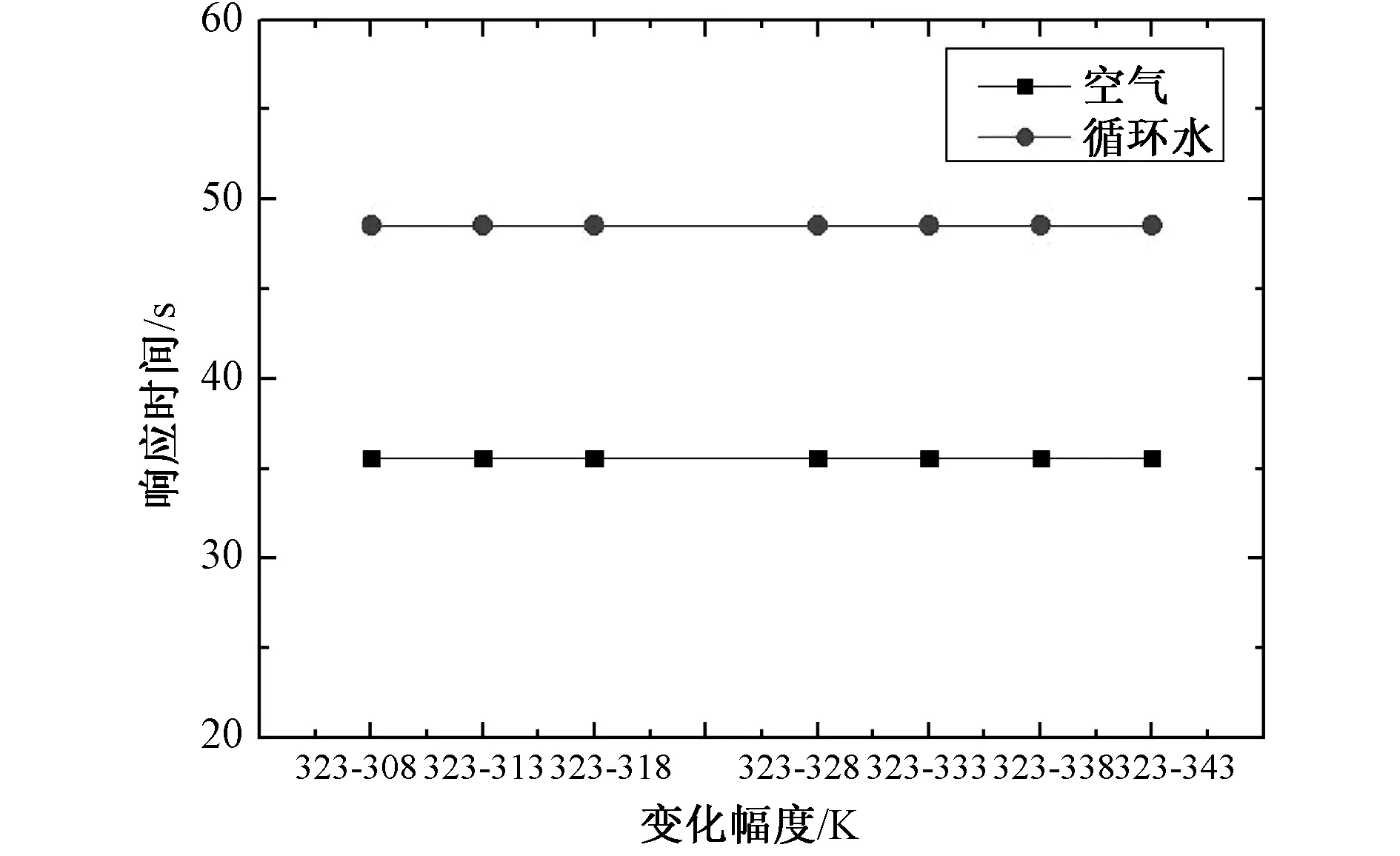
图8 循环水入口温度变化时的响应时间Fig.8 Response time with water inlet temperature variation
3 结 论
本文研究了迎面风速、循环水质量流量和入口水温阶跃变化时空冷散热器的动态响应特性,获得了变量变化程度不同时对换热器动态响应过程的影响,所得结论主要如下。
(1)迎面风速变化程度越大,对应的动态响应曲线变化幅度也越大。迎面风速升高时,空气和循环水的出口温度均会降低。迎面风速降低时,则趋势相反。迎面风速越大,动态响应时间越短。
(2)循环水质量流量变化程度越大,对应的动态响应曲线变化幅度也越大。循环水质量流量增加时,空气和循环水的出口温度均会增加。循环水质量流量降低时,则有相反的变化规律。循环水质量流量越大,动态响应时间越短。
(3)循环水入口温度变化程度越大,对应动态响应曲线变化幅度也越大。循环水入口温度增加时,空气和循环水出口温度均会增加。循环水入口温度降低时,空气和循环水出口温度变化趋势相反。循环水温度变化程度对响应时间没有影响。
