(2+1)维广义柱Kadomtsev-Petviashvilli方程的Painlevé分析及精确解

唐晓苓 刘汉泽

(聊城大学 数学科学学院,山东 聊城 252059)

0 引言

目前,研究非线性偏微分方程可积性的方法已经有很多种.其中, 在1983年由Weiss,Tabor和Carnevale(WTC)发展的Painlevé分析[1]法是最有效的方法之一, Painlevé分析法通常被称作WTC方法,将WTC方法应用到非线性偏微分方程组[2，3]中,不仅可以得到可积和不可积模型的严格解,还可以得到诸如Painlevé性质[4],Lax对,双线性型,Bäcklund变换[5-8]等性质.在求解常系数非线性发展方程过程中,这种方法用得比较多.而在研究变系数非线性发展方程过程中,这种方法的研究使用比较少见,因此变系数的非线性发展方程在近年来受到越来越多的关注[9-12].

下面研究被数学家和物理学家普遍感兴趣的方程之一(2+1)维广义柱Kadomtsev- Petviashvilli(KP) 方程[13,14]

(ut+6a(t)uux+b(t)uxxx)x+c(t)ux+d(t)uyy=0,

(1)

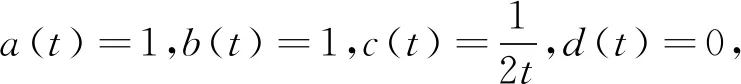
(2)

(3)

数学物理中有很多模型是通过变系数偏微分方程来描述的,因此用Painlevé分析法求它们的精确解具有非常重要的意义.

1 (2+1)维变系数Kadomtsev-Petviashvilli方程的Painlevé分析

Painlevé分析法最初用于常微分方程(组)的解及其研究,是由Painlevé(法国数学家)及其学派提出的.Painlevé分析的WTC方法就是将Painlevé的判别方法推广到非线性偏微分方程的求解中.具体情况如下,如果用WTC方法考虑一个给定的非线性偏微分方程

N(u(z1,z2,…，zn))=0.

(4)

设该非线性偏微分方程的解具有如下展开式形式

(5)

其中φ是一个解析函数,ρ是一个整数,uj则通过Painlevé展开式代入原方程,比较同次幂,并另其系数等于零,从而求得uj(j=0,1,2,…)的值,寻找共振点,检验相容性条件.

对于(2+1)维广义柱变系数Kadomtsev-Petviashvilli方程

(ut+6a(t)uux+b(t)uxxx)x+c(t)ux+d(t)uyy=0,

(6)

其中取c(t)=1,d(t)=1.则方程变为

(ut+6a(t)uux+b(t)uxxx)x+ux+uyy=0.

(7)

假设方程(7)有如下形式的解

(8)

其中q是正整数,uj,φ为x,y,t的函数形式(j=1,2,…).

为了确定常数q,我们假设

u≈u0φ-q.

(9)

再对u≈u0φ-q中的x,y,t求偏导,可以得到

ut=-qv0φ-q-1φt,ux=-qu0φ-q-1φx,

(10)

(11)

(12)

(13)

将(10)-(13)代入方程组(7)可以得到

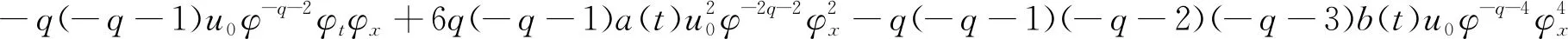
(14)

比较φ的最低次幂可以推出

q=2,

(15)

将(15)代入(14)可以得到

(16)

u=uoφ-2+u1φ-1+u2+u3φ+…+vj-3φj-4+…+vjφj-2+…

uxxxx=u0xxxxφ-2+u1xxxxφ-1+u2xxxx+…+ujxxxxφj-2+…+4[-2u0xxxφ-3-u1xxxφ-2+…

+4[-2u0xxφ-3+u1xxφ-2+…+(j-2)ujxxφj-3+…]φxx+4[-2u0xφ-3+u1xφ-2+…

+(j-2)ujxφj-3+…]φxxx+[120u0φ-6-24u1φ-5+…+(j-2)(j-3)(j-4)(j-5)ujφj-6

+(j-2)(j-3)ujxφj-4+…]φxφxxx+[-2u0φ-3+u1φ-2+…+(j-2)ujφj-3+…]φxxxx.

(17)

为了计算共振点,将(17)代入(7),通过比较φ的各次幂系数可以得到

(18)

(19)

将(16)式代入(19)式,可以计算出

(20)

(21)

(16)式和(20)式代入(21)式,可以计算出

(22)

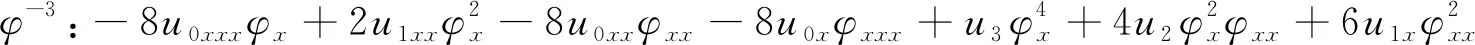
(23)

显然,u3可以由(16),(20)和(22)求出

(24)

但是用类似的计算方法却无法求出u4,u5,u6原因是

φj-6:=[(j-2)(j-3)(j-4)(j-5)u(j-2)t]φtx+6[(j-2)(j-3)(j-4)(j-5)u(j-3)x]φx

+[(j-2)(j-3)(j-4)(j-5)u(j-3)xx]φxx+[(j-2)(j-3)(j-4)(j-5)u(j-3)x]φxxx

+b(t)u(j-4)yy+2b(t)[(j-2)(j-3)(j-4)(j-5)(j-6)u(j-3)]φy

=0.

(25)

在上式中uj的系数可以写成

(j+1)(j-4)(j-5)(j-6)uj=F(u0,u1,u2,…,uj-1,φx,φt,φtx,φyy,…),

(26)

并且(26)式中的右端只与低于uj的u0,u1,u2,…,uj-1,及φx,φt,φtx,φyy,…有关,当j=-1,4,5,6时uj的系数为零,因此j=-1,4,5,6为方程的(7)的共振点,所以j=-1,4,5,6无法求出,其他的uj可以通过(26)式求出.

若取u4=u5=u6=0,则从(26)知u7=u8=…=0,此时(8)式是有限项,即

u=u0φ-2+u1φ-1+u2+u3φ，

(27)

其中u0,u1,u2,u3由(16),(20),(22)和(24)确定.

2 (2+1)维变系数Kadomtsev-Petviashvilli方程的精确解及其解图像

通过上述计算可知(2+1)维广义圆柱变系数Kadomtsev-Petviashvilli方程的精确解u=u0φ-2+u1φ-1+u2+u3φ,其中我们还要确定函φ,因为u0,u1,u2,u3由(16),(20),(22)和(24)确定,我们假设φ可以表示为指数函数形式

(28)

其中η(y,t)是关于y,t的待定函数,ω(t)是关于t的待定函数,将φ代入(16),(20),(22)和(24)中,可以得到关于η(y,t)的一个特解

η(y,t)=f1(t)y+f2(t),

(29)

其中f1(t),f2(t)都是关于t的函数.

将(29)代入(28)可以得到

(30)

再将(29)和(30)式代入(24)式中,可以得到

(31)

将(16),(20),(22),(24),(30)和(31)代入u=u0φ-2+u1φ-1+u2+u3φ中,即得到(7)的精确解

(32)

其中ω(t)由(31)式决定.上述解是一个新解,还未被其他文献描述过.图1(a)刻画了最终解的一个结构图,其中a(t)=sin(t),b(t)=cos(t),f1(t)=t,f2(t)=t+1,k=0,ω(t)=sin(t)cos(t).

f1(t),f2(t)为光滑函数,在这一部分当中,我们用Maple将(16),(20),(22),(24),(30),(31)和(32)代入u=u0φ-2+u1φ-1+u2+u3φ中,方程(7)成立,其解满足方程.

3 总结

首先,这篇文章对(2+1)维变系数Kadomtsev-Petviashvilli方程进行了Painlevé分析,其次,用Painlevé分析的WTC方法得到了(2+1)维广义柱Kadomtsev-Petviashvilli方程新的精确解,并用Maple对其解的正确性进行了验证,其中f1(t),f2(t)为光滑函数,这会使得到的空间结构图更加丰富,若取不同的参数值,便会得到不同的图形.