加强问题设计 落实数学核心素养
2020-04-09徐正忠
徐正忠


在数学教学过程中,不仅要落实基本知识、基本技能和基本数学思想,而且要在这学习活动过程中,在学生获得解决问题的基本经验和基本能力的基础上,再将现实问题利用数学建模的方法手段,抽象为数学问题,然后应用数学的推理、运算、分析等方法来解决,从而提升学生的数学思维能力,经反复训练研究,学生思考问题的能力螺旋上升,以此让学生养成 “会用数学的眼光观察现实世界,会用数学的思维思考现实世界,会用数学的语言表达现实世界”,全面提高学生的数学素养,达到数学学习的最高境界。
本人想从学生已有的基本问题(教材、练习册提供的基本问题),问题的条件单一,即思考为一个维度,其包含简单的计算,简单解方程等为起点,然后增加问题变量,使原简单问题更贴近现实生活中的现实问题,这样设计问题方法,其意义就是增加解决问题的维度,提高训练难度和深度,通过学生对数学问题的解决,达到落实数学核心素养的目的。
一、基本问题的设计,为学生解决后续问题提供阶梯
问题1:有一位企业家为建造一所希望学校,现甲仓库共有50吨的水泥,请一家运输公司把它运到距甲仓库20千米的A 地,其运价费为100元/千米,则这位企业家支付给这家运输公司的总运费为多少元?
问题2:有一位企业家为建造一所希望学校,现甲仓库共有50吨的水泥,请一家运输公司把它运到距甲仓库20千米的A 地,其运输价为30元/吨,则这位企业家支付给这家运输公司的总运费为多少元?
问题3:有一位企业家为建造一所希望学校,现甲仓库共有50吨的水泥,请一家运输公司把它运到距甲仓库20千米的A 地,其运输价为20元/千米·吨,则这位企业家支付给这家运输公司的总运费为多少元?
问题4:有一位企业家为建造一所希望学校,现甲仓库共有x吨的水泥,请一家运输公司把它运到距甲仓库20千米的A 地,其运输价位20元/千米·吨,则这位企业家支付给这家运输公司的总运费为多少元?(用x的式子表示)
问题5:有一位企业家为建造一所希望学校,现甲仓库共有50吨的水泥,请一家运输公司把它运到距甲仓库20千米的A 地和25千米的B地,其中A地需要x,甲仓库到A、B两地的运价分别是12元/千米.吨和10元/千米.吨,则这位企业家支付给这家运输公司的总运费为多少元?
这些基本问题的设计和解决,一方面巩固学生的基本知识,理顺知识点之间的关系,同时给学生后续问题的解决提供方法和阶梯。
二、探究问题、解决问题 ,提升学生的思维能力
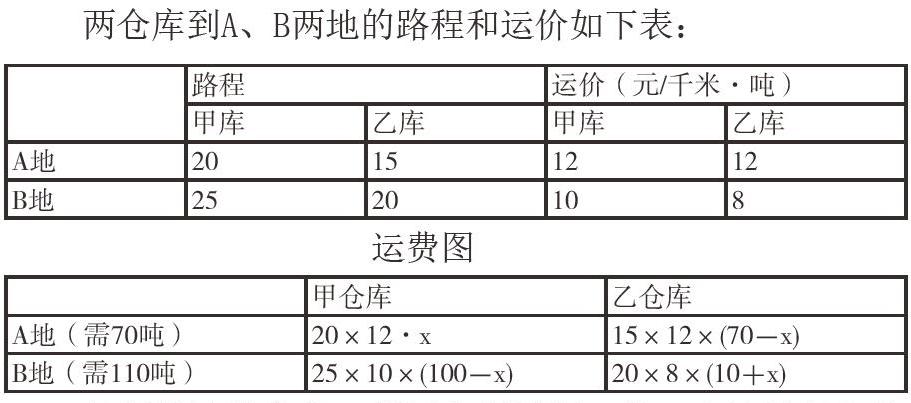
有一位企业家为建造一所希望学校,将甲乙两个仓库中的水泥运送到A、B地,已知甲仓库可调出水泥100吨,乙仓库可调出水泥80噸;A地需要水泥70吨,B地需要水泥110吨。两仓库到A、B两地的路程和运价如下表:
问题1:设甲仓库运往A地水泥x吨,求总运费y(元)用x(吨)的代数式表示及x的取值范围。
问题2:设计一个调配方案,使总运费最省。
分析:从上述问题可知,求总运费,必须求出甲乙两库到A、B两地运费各是多少,要求出仓库到目的地的运费,必须知道他们之间的路程,运送的数量,才能求出运费。因此设计一个数量调配图和一个运费图
两仓库到A、B两地的路程和运价如下表:
问题设计的意义:利用方程思想,将一个比较复杂的问题用较为简单的方法解决,同时得到最优化的方案;在日常实际生活中,设计活动方案时,我们要做最优化的研究,使投入得精力、财力最少,而结果最理想,学习数学的目的是用数学解决我们生活中遇到的问题。从影响问题的维度来看:货物的运价与发货仓库和工地之间路程的长短及运输货物的数量有关,即运价的多少受问题两个条件影响,也就是思考问题为两个维度,学生的解决问题能力从一个维度提升为两个维度,不仅扩充了学生思维容量,同时数学问题也较好贴近现实生活问题,使数学问题更有现实意义。
三、对问题设计的几点思考
1.问题的设计原则要有层次性,即有简单到复杂,思考的维度从单维到多维。
2.问题的设计离不开数学知识,开展数学问题研究的基础是学生掌握了相当数量的应用数学知识,因此教师要通过练习来培养学生基本的数学理念,本设计利用学生熟悉教材提供的基本问题,计算出从某地到另一地的运费,引导学生找到解决和设计问题的方案,即用字母x来表示甲乙两仓库到A、B两地的运费,从而求出总运费,并找到运费最少的最佳方案,在教学实践中,这个问题的设计是成功的,把本来对六年级学生来说比较难的最优化问题,通过这个通联问题,使学生较容易的理解且能解决。
3.问题的设计和解决,其主阵地为课堂,其抓手是教材和学生比较熟悉的素材,同时问题难度要适当高于教材问题,引发探究的兴趣,但要符合学生的学习年龄段和现有的知识基础。
4.问题设计和探究的目的,是激发学生的学习兴趣和培养学生的学习能力,从而提高学生的数学素养。上述问题的解决过程,使学生进一步掌握了利用一元一次方程解决实际问题的方法,形成了良好的数学思维习惯和应用意识,提高了自己解决问题的能力,同时感受到数学所带来的乐趣,增进了学好数学的信心,并且对数学有了进一步的体验和理解。
5.要使在数学活动过程中取得良好的效果,问题的设计符合学生的认知结构是前提。最佳方案问题,是问题设计中的常见内容,对初中六年级学生来说的确是一个难理解的问题,但是,只要在问题设计做好铺垫,即利用他们已有的知识,搭好“阶梯”,问题解决就容易些,从而问题得到圆满的解决。
