基于加权BF-TOPSIS的多属性决策方法研究

宋建新 熊俊芬 刘海桥

摘   要：BF-TOPSIS算法结合置信方程和TOPSIS算法，能够有效处理多属性决策问题。加权BF-TOPSIS（WBF-TOPSIS）算法是对BF-TOPSIS算法的有效推广，保留了BF-TOPSIS算法的优越性。文章首先对BF-TOPSIS算法的归一化问题进行详细推理分析，并给出BBAs构造的一种新的证明。通过分析BF-TOPSIS算法BBAs构造的实际意义，提出WBF-TOPSIS算法，并给出加权系数的最优化表达式。BF-TOPSIS算法是WBF-TOPSIS算法的一种特殊情况。相比于BF-TOPSIS算法，WBF-TOPSIS算法能够做出更优的决策结果;最后算例分析验证了所提算法处理多属性决策问题的优越性性。

关键词：多属性决策;置信方程;TOPSIS;信息融合

1    算法介绍

多属性决策（Multiple Criteria Decision Making，MCDM）[1-2]是在一定数量的备选方案上进行偏好决策，已广泛应用于安全性分析、风险评估、故障诊断等不同领域[3-6]。传统的多属性决策方法有层次分析法[7-9]（Analytical Hierarchy Process，AHP）、[10-12]（Technique Order Preference by Similarity to Ideal Solution，TOPSIS）方法、评价排序向量法[13]（Estimator Ranking Vector，ERV）、有序加权平均算子[14]（Ordered Weighted Averaging，OWA）等方法。

MCDM虽然易于表达，但是处理实际问题时，并不利于问题的解决，因为在实际工程应用中，属性值量纲不同、标准不同，甚至不同的信源之间的属性值存在冲突。因此，有必要对常规的MCDM方法进行改进，其中，模糊Dempster MCDM方法[15]是Deng教授基于不确定环境下MCDM问题提出的，结合了模糊集理论（FST）和证据理论（DST），有效地处理了供应商选择问题。Shaverdi[16]利用Fuzzy AHP和Fuzzy TOPSIS提出一种新的业绩评估方法，通过分析发现，在不确定的环境下，模糊MCDM决策方法比传统的MCDM决策方法更合适、有效。Zhang[17]针对经典TOPSIS的可比性问题，提出一种新的基于加权灰色关联系数的改进TOPSIS方法，将经典TOPSIS和灰色关联分析的优势集成在数据序列处理中的曲线位置和曲线趋势上，从而得到更能满足评估精度和稳定性的要求。Dezert[18]基于置信方程[19-21]提出新的BF-TOPSIS方法，BF-TOPSIS算法能够有效避免数据归一化处理，并且不存在排序反转现象。

本文将研究不确定信息的多属性决策，考虑到置信方程（即证据理论）在不确定信息表征、不确定推理方面的研究较为成熟，并且BF-TOPSIS方法很好地解决了TOPSIS反转现象。所以，本文将基于BF-TOPSIS对不确定信息的多属性决策问题进行研究，但是BF-TOPSIS在构造置信概率赋值（BPA）时，不确定区间较大，不利于后续的融合决策，鉴于此，本文基于BF-TOPSIS提出加权BF-TOPSIS（WBF-TOPSIS）。

本文所给出的算法WBP-TOPSIS是对BF-TOPSIS算法的有效拓展。通过分析算法BBAs的构造可以看出，WBF-TOPSIS算法中的BBAs构造是BF-TOPSIS算法和数据归一化处理的有效综合。通过改变WBF-TOPSIS算法中参数α的值，可以有效控制构造出的BBAs中模糊区间大小。本文通过分析，给出加权系数的最优化表达式。

本文首先介绍了BF-TOPSIS的4种算法;其次，分析了BF-TOPSIS的归一化问题，并给出BF-TOPSIS算法BBAs构造的一种新的证明;再次，给出WBF-TOPSIS算法的定义并进行相关分析，推导出加权系数的最优化表达式;从次，结合BF-TOPSIS和WBF-TOPSIS算法进行单属性决策和多属性决策算例分析;最后做出总结。

2    理论基础

BF-TOPSIS是结合置信方程和TOPSIS的多属性决策算法，记多属性决策中的决策矩阵为S=[Sij]M×N，其中，M>1表示目标Ai个数，N≥1表示属性Cj个数，第j列，表示Cj对目标作出的决策。记多属性决策结果为置信函数理论中的识别框架，对于命题，记：

3     BF-TOPSIS相关问题分析

3.1  BF-TOPSIS的归一化问题

所以BF-TOPSIS算法在构造BBAs时必须要满足不等式（2），Dezert等给出不等式（2）的详细证明过程，本文将给出BF-TOPSIS算法BBAs构造的一种新的解释。

如图1所示，将传感器Cj的决策向量从小到大排序，并表示成柱状图的形式，横坐标表示决策目标Ai，纵坐标表示传感器Cj对目标Ai的决策量Sij，曲线表示排序后决策量Sij的包络。一般地，考虑传感器Cj对目标Ak的BBAs构造过程，虚线l表示决策量Skj，结合公式（1）可以得到，积极证据支持度就等于虚线l下方浅绿色区域决策量之和，即：

4    加权BF-TOPSIS

4.1  新的加权BF-TOPSIS方法

Dezert基于置信方程提出的新的BF-TOPSIS方法很好地解决了TOPSIS反转现象。BF-TOPSIS在构造置信概率赋值（BPA）时，不确定区间较大（在后续的算例中有所體现），不利于后续的融合决策，鉴于此，本文基于BF-TOPSIS提出加权BF-TOPSIS（WBF-TOPSIS）。

置信区间的区间长度表示不确定度，通过分析式（5—7）及图1可以发现，构造出的BBAs不确定度主要是由图1中②④两块区域的置信度决定，即S∑2，S∑4决定了不确定度，其中：

当α=1时，WBF-TOPSIS的BBAs构造公式退化为归一化公式，此时的BBAsm（·）只与相关，丢失了部分信息量，但是，不確定度为0，问题退化为概率问题。

当α∈（0，1）时，如图2所示，红线表示WBF-TOPSIS中BBAs构造的，蓝线表示WBF-TOPSIS中BBAs构造的，阴影部分表示不确定区间，随着α从0→1变化时，不确定区间长度线性减少。

对WBF-TOPSIS中构造出来的BBAs相应的有4种处理方式，处理方式与BF-TOPSIS算法一样。

4.2  加权系数α的最优化

加权系数α可以取[0，1]中的任何一个值，不同的α取值，影响着BPA的生成，从而影响最终的决策效果。在此将对加权系数α进行分析，研究得到最优的加权系数。

通过上述分析可以得到，当α=0时，WBF-TOPSIS退化为BF-TOPSIS，而当α=1时，WBF-TOPSIS的BBAs构造公式退化为归一化公式。所以，α的取值取决于多属性的决策数据的性质。如果原始数据利用BF-TOPSIS更有利于决策，则α就变小，相反，如果原始数据利用归一化更有利于决策，则α就变大。

分析原始数据可以发现，当决策数据中，较优的决策值很少，而差的决策值相对较多时，决策的不确定性较小，如图3（a）所示，此时适合直接归一化得到BPA赋值，从而降低BPA的不确定区间的长度，此时的加权系数α应该偏大。而当决策值相对均匀分布时，如图3（b）所示，此时适合利用BF-TOPSIS方法得到BPA赋值，利用证据理论的优点，对不确定证据进行决策，此时的加权系数α应该偏小。

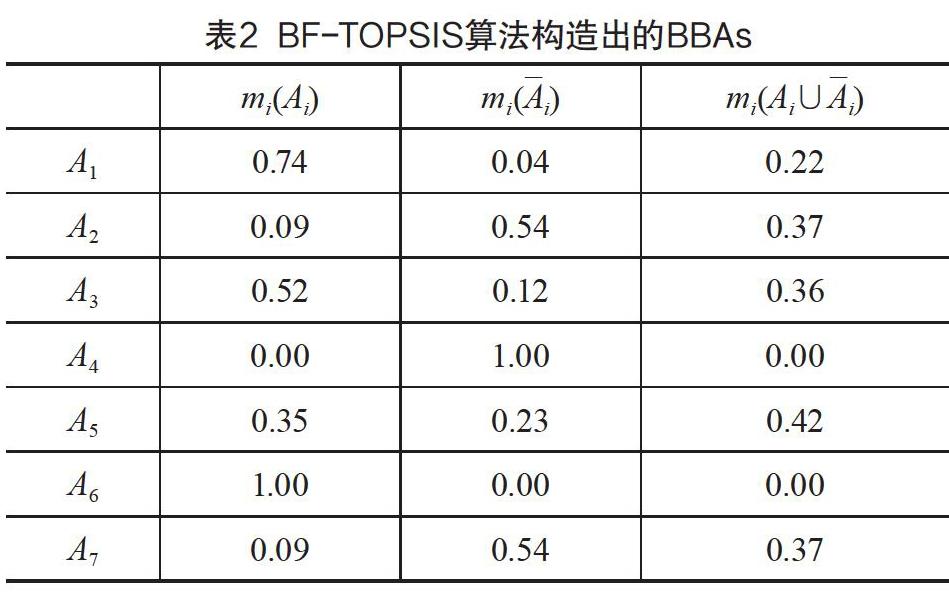
从决策可以看出，信源倾向于对命题A4作出决策，其余命题的信度都较差。而从表1中的数据可以看出，通过BF-TOPSIS构造出的BPA将较多的信度赋予了全集Ai∪ _Ai），而通过WBF-TOPSIS构造出来的BPA将较多的信度赋予了命题的非 _Ai，从而可以看出，在加权系数aj的优化下，WBF-TOPSIS得到了更优的BPA赋值。

5    基于WBF-TOPSIS的多属性决策算例分析

5.1  单属性算例分析

考虑单个属性C1。假设目标可能决策结果为Ai（i=1，…，7），相应地给出C1的决策向量（收益向量，值越大越优）S1=[90，50，80，30，70，100，50]，如果对决策向量直接排序，可以得到决策结果：

结果表明，WBF-TOPSIS可以有效地处理单属性目标决策问题。文章在此通过算例介绍了WBF-TOPSIS算法的一般步骤，并论证了算法的有效性，下面将具体结合案例，分析WBF-TOPSIS在多属性决策中的应用。

5.2  多属性算例分析

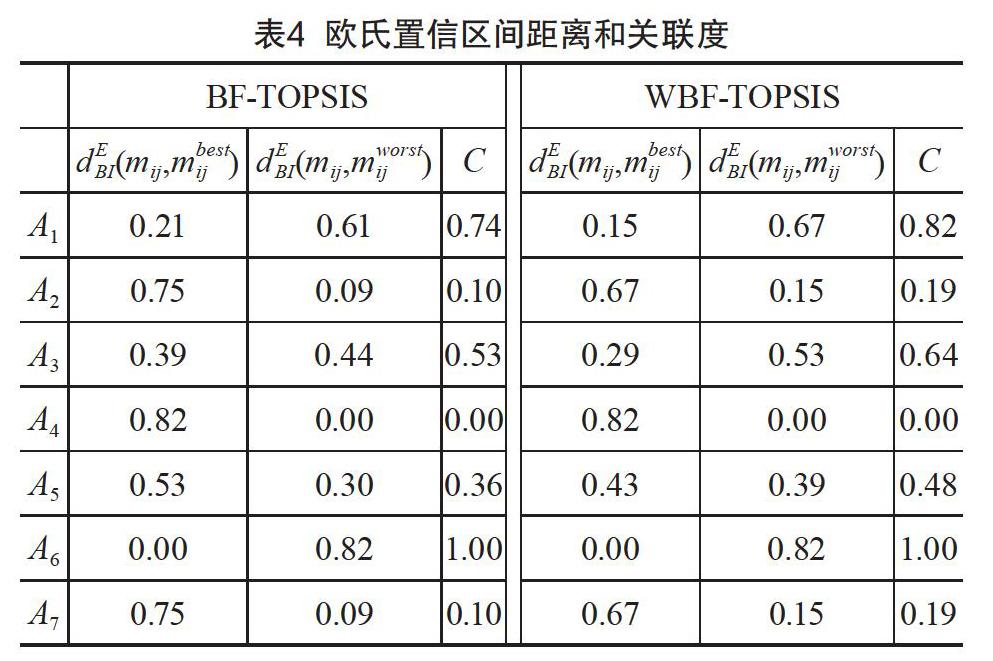
分别用BF-TOPSIS1-3和WBP-TOPSIS1-3对上述问题进行处理，其中WBP-TOPSIS1-3中参数a分别取0.1～0.9，步长为0.1，计算得到关联度C，结果如图4—6所示。

当a取0时，WBF-TOPSIS与BF-TOPSIS计算出来的关联度C相同，随着a的不断增大，WBF-TOPSIS的运行结果明显优于BF-TOPSIS的结果，很好地验证了算法的优越性。

6    结语

本文对BF-TOPSIS算法进行推广，提出WBF-TOPSIS算法。WBF-TOPSIS继承了BF-TOPSIS算法优点—避免了对数据归一化处理以及有效解决了排序反转现象。通过对BF-TOPSIS算法的归一化问题进行详细的推理论证，可以得到BF-TOPSIS算法在构造BBAs过程中蕴含了归一化过程;给出BF-TOPSIS算法的BBAs构造的新的证明，并在此基础上，引出WBF-TOPSIS算法，通过对所提算法的分析，可以发现：WBF-TOPSIS算法是BF-TOPSIS算法与直接归一化处理手段的有效综合。最后，文章给出了WBF-TOPSIS1-3算法的一般步骤，算例结果验证了所提算法的有效性。

[参考文献]

[1]GAVADE R K.Multi-criteria decision making：an overview of different selection problems and methods[J].International Journal of Computer Science&Information Technologies，2014（4）：5643-5646.

[2]DODGSON J S，SPACKMAN M，PEARMAN A D，et al.Multi-criteria analysis：a manual[J].Economic History Working Papers，2009（1）：113-118.

[3]TERVONEN T，NACI H，VALKENHOEF G V，et al.Applying multiple criteria decision analysis to comparative benefit-risk assessment：choosing among statins in primary prevention[J].Medical Decision Making，2015（7）：859.

[4]TZENG G H，HUANG J J.Multiple attribute decision making：methods and applications[J].Lecture Notes in Economics&Mathematical Systems，2010（4）：520-531.

[5]YANG H，LAI C，YU H，et al.Multiple-criteria decision analysis：public values influence on participation in unused medicine recycling[J].Journal of Applied Sciences，2016（6）：262-270.

[6]MARSH K，IJZERMAN M，THOKALA P，et al.Multiple criteria decision analysis for health care decision making-emerging good practices：report 2 of the ispor mcda emerging good practices task force[J].Value in Health the Journal of the International Society for Pharmaco economics&Outcomes Research，2016（2）：125.

[7]SAATY T L.How to make a decision：the analytic hierarchy process[J].European Journal of Operational Research，1990（1）：9-26.

[8]TAKAHASHI I.AHP applied to binary and ternary comparisons[J].Journal of the Operations Research Society of Japan，2017（3）：199-206.

[9]LI S，LI J Z.Hybridising human judgment，AHP，simulation and a fuzzy expert system for strategy formulation under uncertainty[J].Expert Systems with Applications，2017（3）：5557-5564.

[10]LAI Y J，LIU T Y，HWANG C L.TOPSIS for MODM[J].European Journal of Operational Research，1994（3）：486-500.

[11]VOMMI V B.TOPSIS with statistical distances：a new approach to MADM[J].Decision Science Letters，2017（1）：49-66.

[12]SANGAIAH A K，GOPAL J，BASU A，et al.An integrated fuzzy DEMATEL，TOPSIS，and ELECTRE approach for evaluating knowledge transfer effectiveness with reference to GSD project outcome[J].Neural Computing&Applications，2017（4）：1-13.

[13]YIN H，LAN J，LI X R.Measures for ranking estimation performance based on single or multiple performance metrics[C].Istanbul：International Conference on Information Fusion IEEE，2013.

[14]NGUYEN J，S?NCHEZ H G，AGELL N，et al.Evaluating student-internship fit using fuzzy linguistic terms and a fuzzy OWA operator[C].Beijing：IEEE International Conference on Fuzzy Systems，2017.

[15]DENG Y，CHAN F T S.A new fuzzy dempster MCDM method and its application in supplier selection[J].Expert Systems with Applications，2011（8）：9854-9861.

[16]SHAVERDI M，RAMEZANI I，TAHMASEBI R，et al.Combining fuzzy AHP and fuzzy TOPSIS with financial ratios to design a novel performance evaluation model[J].International Journal of Fuzzy Systems，2016（2）：248-262.

[17]ZHANG Z，WANG Y，WANG Z.A grey TOPSIS method based on weighted relational coefficient[C].Nanjing：IEEE International Conference on Grey Systems and Intelligent Services，2014.

[18]DEZERT J，HAN D，YIN H.A new belief function based approach for multi-criteria decision-making support[C].Heidelberg：International Conference on Information Fusion IEEE，2016.

[19]HAN D，DEZERT J，DUAN Z.Evaluation of probability transformations of belief functions for decision making[J].IEEE Transactions on Systems Man&Cybernetics Systems，2016（1）：1-18.

[20]YANG Y，HAN D.A new distance-based total uncertainty measure in the theory of belief functions[J].Knowledge-Based Systems，2016（6）：114-123.

[21]KERKVLIET T，MEESTER R.A Behavioral Interpretation of belief functions[J].Journal of Theoretical Probability，2017（7）：1-17.

[22]HAN D J，DEZERT Y Y.New distance measures of evidence based on belief intervals[C].Oxford：in Processing of Belief，2014.

[23]HAN D，DEZERT J，YANG Y.Belief interval-based distance measures in the theory of belief functions[J].IEEE Transactions on Systems Man&Cybernetics Systems，2016（3）：1-18.

[24]IRPINO，ANTONIO，VERDE，et al.Dynamic clustering of interval data using a Wasserstein-based distance[J].Pattern Recognition Letters，2008（11）：1648-1658.