基于FIR与相位补偿IIR滤波器的雷达回波信号处理
2020-04-09王光宇
王光宇

摘 要:FIR與IIR频率选择滤波器的设计,被广泛应用于数字信号处理领域之中。文章以雷达回波信号的数字处理为例,首先分别设计FIR,IIR滤波器完成了对信号特定频率分量的滤除。进而,针对IIR滤波器的非线性相位,基于最优化设计全通系统实现了相位补偿,并对FIR,IIR滤波器进行了综合比较。
关键词:无限冲激响应数字滤波器;有限冲激响应数字滤波器;全通系统;相位补偿
根据冲激响应的长度是否有限,可以将数字滤波器划分为无限冲激响应(Infinite Impulse Response,IIR)滤波器和有限冲激响应(Finite Impulse Response,FIR)滤波器。根据实际要求,合理选择滤波器的类别,在实现预期效果的同时尽可能降低成本,具有重要现实意义。
1 雷达回波信号的模拟
假设雷达回波信号包含载频50 MHz,带宽10 MHz,时宽10 μs的线性调频脉冲信号和20 MHz,80 MHz的正弦波,即:
2 数字滤波器设计的基本理论
根据广义线性相位系统的充分条件[1]知,h[n]为有限长偶对称序列,因此FIR数字滤波器具有线性相位、恒定群延迟,不会造成信号的相位失真。
对于频率选择性IIR数字滤波器的设计,通常是根据经典模拟滤波器原型,采用双线性变换法[2]实现,且模拟频率Ω与数字频率ω之间的映射关系为:
3.2 求解最优全通补偿系统的算法描述
在式(6)所示规划问题时,设计不同阶数的全通系统(即在一定范围内遍历N的取值),并在每一固定阶数下求解关于损失函数最小的无约束最优化问题,然后权衡系统阶数、极点分布情况对初代最优解进行筛选,得到最优补偿系统设计。具体步骤如下。
Algorithm 1:最优相位补偿系统设计算法。
Step 1:初始化系统阶数N。
Step 2:在当前N下,初始化系统函数(对应于式(4))的各阶系数{ak|k=1,2,…,N}。
Step 3:计算由当前N、{ak|k=1,2,…, N}决定的补偿系统损失函数FCost,若优化算法收敛,输出系统阶数N、各阶系数{ak|k=1,2,…,N}、损失函数FCost及相关量化指标;否则,基于算法搜索原则,更新各阶系数。
Step 4:重复Step 3,直至算法收敛,记录相关参数与结果。
Step 5:更新网络阶数N,重复Step 2~Step 4,得到多组阶数N下的损失函数FCost及各阶系数{ak|k=1,2,…,N}。
Step 6:结合量化指标及对相位曲线拟合度的直观判断,得到最优阶数N与最优系统各阶系数{ak|k=1,2,…,N},完成最优相位补偿系统设计。
在实际有限精度计算中,需要对系统频率响应进行抽样分析,本次实验中选取抽样点数η=256。
4 设计结果与分析
4.1 滤波器效果的评价指标
考虑以均方误差MSE、平均绝对误差MAE作为量化指标,衡量处理后信号时域波形与线性调频脉冲时域波形的吻合程度,定义如下:
4.2 相位补偿效果的评价指标
为量化评估全通系统相频响应与理想补偿相位的逼近程度,引入归一化均方根误差LNRMS、最大绝对误差eθmax两项指标,定义如下:
4.3 设计结果与分析
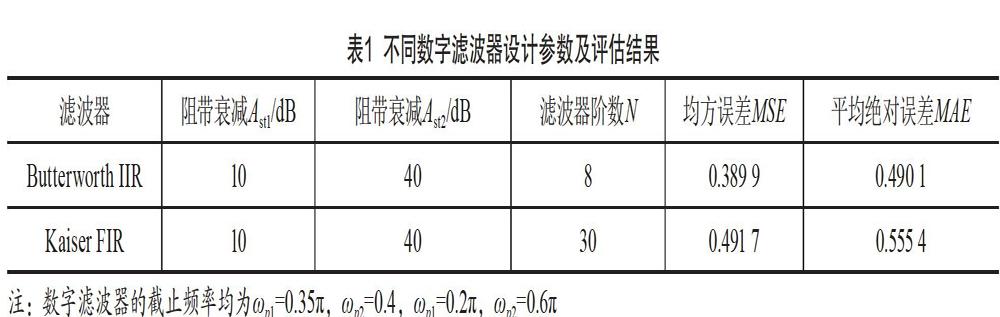
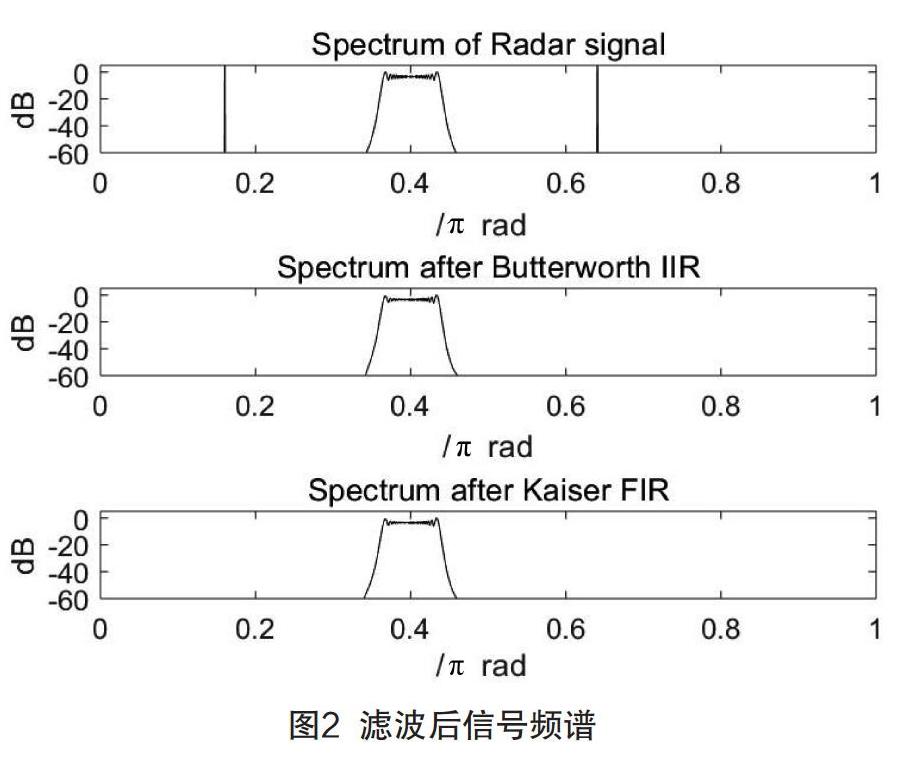
表1为Butterworth IIR、Kaiser FIR滤波器的设计结果,图2绘制了雷达信号经两种滤波器滤波后的幅度谱。可见,在相同技术指标下,Butterworth IIR,Kaiser FIR均完成了对原信号中正弦波成分的滤除;由MSE,MAE知,滤波后信号波形与线性调频脉冲信号逼近良好。由于IIR滤波器采用递归结构实现,如不考虑相位的失真效应,在相同技术指标下,设计Butterworth IIR滤波器仅需要8阶,而设计Kaiser FIR滤波器需要30阶[3]。
表2列出了Butterworth IIR滤波器的最优相位补偿参数,对于8阶Butterworth IIR滤波器,在不严格给定相位误差限制的前提下,按照3.2节算法得到的最优全通系统需要10阶。图3绘制了Butterworth IIR滤波器相位补偿前后的相频响应与群延迟,通过级联全通系统相位补偿后,滤波器相位线性程度显著提高,群延迟的变化幅度减小。通过级联全通系统加以相位补偿,可以明显改善信号的相位失真问题,但将大大提高滤波器系统复杂程度[4]。
5 结语
对于频率选择性滤波器,IIR滤波器以较低阶数即可获得可观的频选特性,系统结构复杂度低、经济高效。但若要避免信号相位的失真,必须级联全通系统加以相位补偿,使整个系统的阶数、复杂性、计算工作量大大提高。FIR滤波器本身具有线性相位,但要获得较高频选特性,需采用较高阶数进行设计,从而增加结构复杂度与信号延迟。因此,IIR和FIR滤波器各有所长,在实际中应统筹考虑各方面因素进行选择。
[参考文献]
[1]PROAKIS J,MANOLAKIS D.Digital signal processing[M].Third edition.London:Pearson Education,2005.
[2]DENG T.Simplified linear-programming method for designing all-pass phase-compensation network[C].Ho Chi Minh City:International Conference on Control,2012.
[3]赵淑清.随机信号分析[M].3版.哈尔滨:哈尔滨工业大学出版社,1996.
[4]DENG T.Minimax design of low-complexity allpass variable fractional-delay digital fifilters[J].IEEE Trans.Circuits Syst.I,2010(8):2075-2086.
