考虑E/T惩罚的产品SERU数量优化

(浙江工业大学 经贸管理学院，浙江 杭州 310023)

在当前的世界经济大环境下，客户对产品的需求日趋个性化、迅速化和多样化(比如：苹果公司在设计出新的iPhone手机后，便要求遍布全球的生产商快速进行各部分零部件的生产。除了手机之外，相关配套充电器和耳机等附属产品也要同时生产。部件生产出来后，中国和东南亚的装配商迅速组装产品并第一时间发货给苹果公司，由其在全世界范围内进行统一发售)。很多国家的生产企业为了适应当前的经济形势，调整了自身的传统流水线生产模式，改为采用更为先进和便捷的生产模式。自1960年开始，日本丰田公司采用U型生产线进行多品种、小批量化产品生产实践和改革。20世纪90年代，日本电子行业中的Sony公司将丰田的精益理念和索尼的单人生产结合起来，拆除冗长的装配式传送带，构建了SERU生产系统。随后，松下、佳能、东芝、日电显示器和理光公司等企业开始采用SERU生产方式进行产品生产。美国戴尔和韩国三星等世界知名企业也相继效仿这种先进的生产模式。20世纪60年代，部分中国企业逐渐采用了单元生产(Cell manufacturing，CM)或成组技术(Group technology，GT)进行传统流水线的改造。SERU和CM生产方式既有相同点，又存在一些差异。SERU和CM都是基于产品或工件的加工工艺进行零部件的分族之后，再将相关机器分配给相应的零部件族并按U型进行机器布置。对于CM[1-2]来讲，由于机器有限导致某个U型加工单元不能满足单元内产品族所有产品的加工需求，因此经常出现跨单元加工的现象。对于SERU而言，尽量保证每个加工单元有足够的机器，使得每个加工单元可以保证加工一个或多个产品族，因此基本不存在跨单元现象。CM和SERU虽然都强调工人的灵活性，但是对交叉培训的重视程度不一样，SERU更加看重工人的技能，所有采用SERU的企业都鼓励工人进行交叉培训，从而使工人获得更多技能。SERU和CM中主要有3 种单元类型：屋台式、逐兔式和分割式。屋台式是来源于日本街头的流动小吃车运作模式，十几种小吃都由老板一人按客人需求制作完成。屋台式的生产特点是整个单元的工作由一个人完成，加工机器的数量充足，工人具备全部技能。屋台式的优点是工序间的调整时间较小，工人的个人成就感强；缺点是个人移动距离相对较长，设备需要量大，工人掌握全部技能的时间长。逐兔式的生产特点是单元内部同时有几个工人进行工作，每个工人单独完成所有加工任务，一个工人完成了当前机器上的加工任务就立刻转到下一个机器上进行操作，从而让出当前的机器给后面的工人使用，工作过程类似于你追我赶的状态。逐兔式的优点是单元得到充分利用，生产效率提高，节省了单元构建成本；缺点是整个单元的效率受制于最慢的工人的工作速度，对于生产节拍的一致性要求高，同样需要掌握全面技能的工人。分割式的生产特点是一个单元内部有几个工人同时作业，每个工人负责几台机器，一个完整的加工任务由几个工人共同协作完成。分割式的优点是不需要全技能工人，交叉培训时间短；缺点是需要工人相互协作保证生产节拍一致性。

在考虑加工单元能力有限、产品的提前期和拖期惩罚以及不同产品间前后加工工具转换成本的前提下，笔者研究了在SERU系统中如何保证产品的按时交货且SERU使用数量最少的问题。研究的意义是在满足产品交货期的情况下，以最小的代价(机器和人员)快速生产所有产品。SERU数量越少意味着节约的机器和人员越多，从而可以使企业在最短的时间内，以最低的成本满足客户需求。在问题求解方面，笔者设计了混合鸡群-教与学算法，通过与基本鸡群算法和教与学算法的比较，验证了混合算法的适用性和有效性。

1 SERU相关研究综述

近年来，学者们逐渐认识到SERU系统涵盖并扩展了CM系统的各个方面，开始转向对SERU系统的研究。Yin等[3]给出了高成本环境下SERU系统对制造业竞争力的启示。通过案例研究表明SERU系统是对精益生产、敏捷生产和单元制造的扩展，解释了索尼和佳能如何应用SERU来提高生产力、改善产品质量和增加生产灵活性，从而使企业能够保持全球竞争力。Yu等[4-5]阐述了SERU生产所带来的利益，给出了传统装配线转换为SERU和短生产线系统的基本原理，针对如何构造混合SERU系统以及如何在混合SERU系统上进行生产调度提供了一些启示。Liu等[6]研究了如何将传送带装配线重新配置为SERU系统的问题。Zhang等[7]针对目前SERU研究主要关注经济绩效，而忽视了环境和社会绩效的现象，研究了SERU生产关键技术对可持续性发展的影响。Kaku[8]对SERU是否是一种可持续自造系统进行了详细的论述，通过实证研究明确了SERU可持续发展的特点。Liu等[9]也对如何在带有可持续发展措施的SERU生产系统中进行生产计划进行了相关研究。Lian等[10]以SERU生产系统为背景，在考虑工人技能集差异和熟练水平差异的情况下，解决了多技能工人分配问题。在多目标问题上，Yu等[5]建立了一个多目标优化模型，研究了总吞吐量时间(TTPT)和总工时(TLH)两种性能，通过对双目标模型的分析，给出解空间、组合复杂性和非凸性等问题数学特性—。Villa等[11]对SERU系统和CM的异同进行了理论分析和阐述。Suer等[12]研究了在SERU系统加工单元能力有限情况下，采用启发式算法解决SERU系统单元数量最小化问题。国内也有很多学者关注到了这一点，如2009年刘晨光等[13]概括总结了日本式单元制造SERU的背景、优劣势、与普通单元制造的区别以及本质特征，最后给出了研究方向。廉洁[14]对设备的SERU构建与生产任务分配的协同进行了决策研究，根据产品需求和机器加工能力将各类同质机器分成了若干相互独立的SERU，同时解决了每个SERU中的任务生产顺序。同样，吴旭辉等[15]针对SERU的优点，提出了一种协同改进算法，将SERU构建和SERU调度子问题进行协同优化，改进了已有算法的不足。

2 问题模型

黄德才[16]研究了交货期限制下的多机调度问题，主要是针对如何合理地调整机器加工顺序进行调度。本研究考虑企业在产品交货期限制下，以最少的加工单元数量完成订单。如果产品不是严格满足交货时间(即产品被提前生产或拖期生产(Earliness/Tardiness))，则产生惩罚成本。此外，考虑各个产品生产过程中，不同产品之间的生产准备时间(Setup time)不同，同时考虑每个SERU的加工能力相同。问题的变量和数学模型为

Pi：第i个产品的加工时间。

Q：SERU的启用成本。

Cj：SERU的加工能力。

di：第i个产品的交货期。

Fi：第i个产品的完成时间。

Aik：0～1变量，表示产品k是否在产品i紧后加工。

N：SERU的最大加工能力。

Xij：0～1变量，表示产品i是否在SERU单元j中加工。

Yj：SERU单元j内的所有产品加工完毕所需要的时间。

Vik：产品i和k之间的机器调整费用矩阵。

Ei：产品i的提前交货惩罚成本。

Ti：产品i的拖期惩罚成本。

m：单元数量。

n：产品总数量。

(1)

s.t.Fk=Fi×Aik+Pk∀k,∀i

(2)

Yj=max(Fi×Xij|i∈1，2，…，n) ∀j

(3)

Yj≤N∀j

(4)

(5)

数学模型中：式(1)表示目标函数是最小化SERU启用数量、提前交货惩罚、拖期交货惩罚和不同产品加工机器的调整准备费用；式(2)表示紧后产品的完工时间是紧前产品的完工时间与紧后产品的加工时间的和(机器的调整时间整合到产品加工时间)；式(3)表示SERU单元j的完工时间是其内部最后完工产品的完工时间；式(4)表示SERU单元j的加工任务量不超过单元加工能力限制；式(5)表示一个产品只能在一个单元进行生产加工。

3 鸡群算法

鸡群算法(Chicken swarm optimization, CSO)是由Meng等[17]于2014年10月在第5次国际群体智能会议(ICSI)上提出的一种新的仿生算法，CSO算法模拟了鸡群的层次结构和鸡群觅食行为。整个鸡群分为很多个由公鸡带领的子群，每个子群包括一只公鸡、几只母鸡和几只雏鸡。不同层次等级的鸡按照不同的觅食移动规律觅食，在完整的等级层次结构制度下，竞争不断发生在不同的鸡群之间，所以不同的鸡群都会有自己一定的觅食能力。该算法具有较快的收敛速度和较好的计算精度。

鸡群算法的基本原理是鸡群在进行觅食行为时会有一种倾向，通过错误的尝试来获得经验和了解不同的情况。此外，它们还会根据经验做出觅食决定，根据觅食经验的多少，分成不同等级。不同等级的鸡构成了一个完整的社会体系，即鸡群。在获取食物的过程中，经验丰富的鸡占主导地位，并有权利分配食物，与之同一社会体系的鸡可以通过其分配或在其边上觅食获得食物，鸡群中的鸡可以偷吃其他鸡群中的食物。根据各层次等级的鸡在鸡群中的觅食行为，实现如下设置：

1)所有子鸡群一般由一只公鸡、多只母鸡和多只雏鸡构成，并形成各自相对独立的群体。

2)根据鸡的适应度值，觅食能力最好的鸡认定是公鸡，最差的是雏鸡。母亲母鸡和雏鸡之间的亲属关系通过简单的随机组合确定。

3)群体中的各种关系将在特定的时间步骤中保持不变，所有特性值将在时间步长之后更新。

4)以公鸡为中心点，其他的鸡则围绕在其周围寻找食物，而它们可以避免其他组别的鸡偷食。雏鸡总是围绕在母亲母鸡的身边搜寻食物，占主导地位的母鸡在公鸡得到食物之后可以优先得到食物。

CSO算法在很多的领域得到了应用，发挥了算法的性能，CSO算法在短时间内发展迅速，逐渐完善成熟。目前，基本CSO算法及其改进算法已经在众多的科研领域得到了广泛且准确的应用，发挥了关键的作用。算法步骤为

1)初始化种群参数。初始配置算法参数，主要是初始化鸡群的种群数量大小、迭代更新次数、种群各层级关系的更新速度、个体位置的维度以及比例。

2)初始化鸡群。根据公鸡的数量将鸡群分成RN组，并将母鸡随机分配给每组。母鸡是随机选择产生的，并根据母鸡中母亲母鸡的数量，依照概率确定母亲母鸡与雏鸡之间的关系。

3)迭代开始，如果满足层级更新要求，则更新鸡群分组和他们之间的关系；否则，根据各自的觅食位置更新公式按等级制度高低进行有序更新，然后计算更新位置后的适应度值。

4)个体位置更新。各个位置更新公式计算形成的最优值与原始值进行比较，如果经过觅食位置更新后的最优值较大，则更新个体位置，否则保持原来位置。

5)在达到最大迭代次数后停止迭代，同时输出最优位置解，如果没有达到最大迭代次数，则返回步骤3)进行迭代循环搜索。

4 教与学算法

教与学算法(TLBO)是在2011年Rao等[18]为了解决机械设计中的优化问题而提出的一种人工智能算法，该算法主要是通过教师的教育来有效影响班级学生，以提高学生学习成绩，通过这种模拟方式进行寻优操作。与其他受自然启发的算法一样，TLBO也是一种基于群体的优化方法，它使用群体中的多个个体来进行全局优化[19]。

教与学算法假设一个班级的学生学习多门课程，学习最好的学生作为老师。学生的学习过程受到老师教学方案Xteacher、班级折中方案Xmean和教学因子TF=(1+rand(0,1))成绩的差值影响Xnew=Xold+r×(Xteacher-TF×Xmean)，r=rand(0,1)。此外，学生的学习方案也受到同伴的影响，如果同伴的成绩不如该学生的学习方案，则新的学习方案Xnew=Xold+r×(Xold-X)；如果同伴的学习方案优于该学生的方案，则新的学习方案Xnew=Xold+r×(X-Xold)。在教学过程中，教的过程和学的过程之后，都要更新每个学生的学习方案。算法执行步骤为

1)初始化学生数目、学习方案和变量的取值范围等参数。

2)计算每名学生的成绩。

3)进入教学阶段：确定学生群体中的教师，计算所有学生的折中学习方案；在教育阶段，执行老师教授课程过程，更新学生学习方案。

4)进入学习阶段：为每名学生随机选择班级内的另一名同伴；学生按照同伴的学习方案进行自身学习方案修正。

5)重复步骤2)～4)，直到满足停止条件，输出最优解。

5 混合算法设计

5.1 问题编码

本研究针对日本式单元制造系统中SERU单元数量优化问题，采用自然数编码方式对产品加工序列进行表示，如X=(5, 4, 6, 3, 2, 1, 7, 15, 10, 13, 8, 14, 9, 12, 11)。序列X表示产品安排在生产单元里进行生产的顺序，产品5首先安排到第1个生产单元，接下来安排产品4，如果产品4加入生产单元后超出了单元的生产能力，则产品4安排到新的生产单元。随后的产品6到产品11，首先试探安排在第1个生产单元，如果生产能力不超出单元能力，则安排产品到该单元进行生产，否则依次试探其他生产单元。如果所有的已经安排产品加工的生产单元都超出能力限制，则安排当前产品到新的生产单元进行加工。因此，某个加工方案可能为(5, 4, 2, 1 | 6, 3, 7 | 15, 10, 9, 12 | 13, 8, 14, 11)。根据方案得到SERU数量为4，再检验每个产品的交付期限，如果产品提前或者拖期交付，则产生相关费用。

5.2 混合算法

由于教与学算法主要用于在求解时计算量比较小并且一致性较高的连续的非线性函数的全局解，而在SERU最开始应用中，是将一条很长的流水加工线逐渐进行拆分，形成多条短生产线，类似于教与学算法中老师教育班级里的学生。在进行一段时间的教学以后老师会根据学生学习的好坏进行分类，形成多个不同的学习圈，将学习圈假定为一条条短生产线，但是教与学算法中的学习圈则是由一位班里学习较好的学生带领学习，学习圈的其他成员由班里成绩较差的学生组成。

而鸡群算法则是根据觅食能力对群体进行分类，觅食最好的作为群里的领导者、指导者和教育者；觅食较好的作为群里的传播者；觅食最差的作为跟随者。从细的方面来说，每个学生所学的科目相当于SERU中每个产品，每条生产线的各个方案就相当于学生们的学习成绩，而映射到鸡群算法则是鸡群中各种鸡的觅食能力，基于两种算法存在一定的可优化性，对两种算法进行混合，可以进一步提升算法的效率，优化生产线。

所以本研究混合鸡群算法和教与学算法，以鸡群算法为主框架，结合教与学算法的教和学思想。混合算法在执行初期保持全局最好解作为“教师”鸡，然后按照鸡群算法分群方法，将1 只公鸡、几只母鸡和几只小鸡随机分配给每个鸡群。在基本鸡群算法中，公鸡自身随机搜索。在混合算法中，公鸡除了自身随机找食过程，同时也会接受全局最好解的经验“教”授过程，可以认为公鸡会偷吃其他公鸡的食物。混合算法中的母鸡除了采用基本鸡群算法的位置更新公式之外，还增加本群公鸡“教”母鸡和母鸡与所有群中随机选择的1 只公鸡或母鸡相互“学习”的过程。混合算法中的小鸡除了跟随母鸡觅食，也加入公鸡“教”小鸡和小鸡之间互相学习的过程。

图1 混合鸡群-教与学算法流程图

6 数值算例

笔者算法的计算环境为Windows 10操作系统、AMD 2.2 GHz CPU、4 G内存和500 G硬盘，算法采用C语言进行编码实现，编译环境为VC++6.0。算法采用了C语言中的结构体和数组的概念，构建鸡群的结构体数组、子群的结构体数组、公鸡群的结构体数组、母鸡群的结构体数组和母鸡与公鸡组合群的结构体数组，每只鸡的结构Chicken{}包括鸡的类别{type: 1表示公鸡；2表示母鸡；3表示小鸡}、鸡的“教师”编号{teacher: 小鸡的教师是各自的母亲鸡；母鸡的教师为本群的公鸡}、鸡所在的群编号{group: 指出当前的鸡所在的子群}和鸡的编码结构数组{Code: 根据产品个数决定的多位自然数编码}。算法的参数为种群大小为50(分为5 个鸡群，每个鸡群1 只公鸡、3 只母鸡和6 只小鸡，每只母鸡带2 只小鸡)，最大迭代次数为产品个数的30倍，算法的学习因子、鸡群算法基本公式参数参考文献[17-18]。

算法的停止准则为达到最大迭代次数，算法的效果评价在最好解、解平均值和达优率3 个方面跟基本教与学算法和基本鸡群算法进行比较。算法采用小规模(产品个数分别为8，16，32，36，40)、中规模(产品个数分别为48，56，64，72，80)和较大规模(产品个数分别为85，90，95，98，100)算例进行算法性能验证，每个规模包含5 组算例，每组算例独立运行30 次，每个单元的启用费用为100。

表1～2中给出了8 个产品的小规模算例产品间生产准备费用和产品基本数据。ei表示产品i的提前交货惩罚费用，ti表示产品i拖期交货的惩罚费用，pi表示产品i的加工时间，di表示产品i的约定交货日期，Ji表示产品i(本文所有数据采用无量纲形式)。表3给出了不同规模、不同数量的产品所对应的单元加工能力。

表1 8 个产品的产品间生产准备费用表

Table 1 Schedule of inter-product preparation costs for 8 products

产品J1J2J3J4J5J6J7J8J101010101010010J210001010101010J31000100101010J410101001010010J510100100101010J610101010100100J70101001010010J810101010100100

表2 8 个产品的基本数据表

表3 不同规模算例的单元连续工作限制表

算例部分给出了小规模问题中8 个产品的问题基本参数和相关费用，其他算例的基本参数和相关费用随机生成。根据表1～2的相关数据，经过计算得到其中一个最好解的自然数序列为(5, 3, 4, 7, 8, 6, 1, 2)，根据这个自然数序列，可以得到生产计划安排如图2所示。其中，产品5，3和2在第1个单元，产品4，7和1在第2个单元，产品8和6在第3个单元，因此得出单元的启用数量为3 个，由于按此调度计划安排，每个产品都不存在提前或拖期交付的情况，因此提前和拖期惩罚费用为0。再查看产品间生产费用表，产品间生产准备费用也为0。综合以上情况，可以明确最好的目标函数值为300。

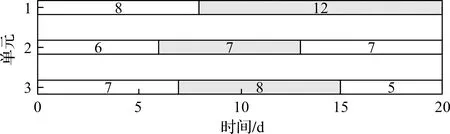
图2 8 个产品的生产调度图

通过大量仿真算例计算，计算结果列于表4，表中列出了产品数量、最好解、解平均值、算法的30 次独立运行中达到最好解的效率、算法的30 次独立运行中平均每次的计算时间以及最好解所对应的单元启用数量。从表4可以看出：针对小规模、中规模和较大规模算例，HA都取得了不错的效果；从最好解方面来看，HA的计算结果取得了所有算例的最好解，而CSO和TLBO针对小规模算例和部分中规模算例取得了最好解，但是对于较大规模算例，CSO和TLBO的计算效果不够理想；从平均值角度来看，CSO和TLBO的计算结果相差不大，无论是小规模、中规模还是大规模，HA的计算结果都明显优于CSO和TLBO；从达优率方面来看，HA的鲁棒性也全面优于CSO和TLBO，HA在小规模问题中的平均达优率高于90%，在中规模问题中的平均达优率近于85%，在较大规模问题中的平均达优率近于80%；从平均计算时间方面来看，HA的计算时间要稍微高于CSO和TLBO算法，这一点可以从HA的特性中看出。由于HA结合两个基本算法的公式，因此在算法执行过程中会多执行一些公式步骤，导致了算法的时间损失。

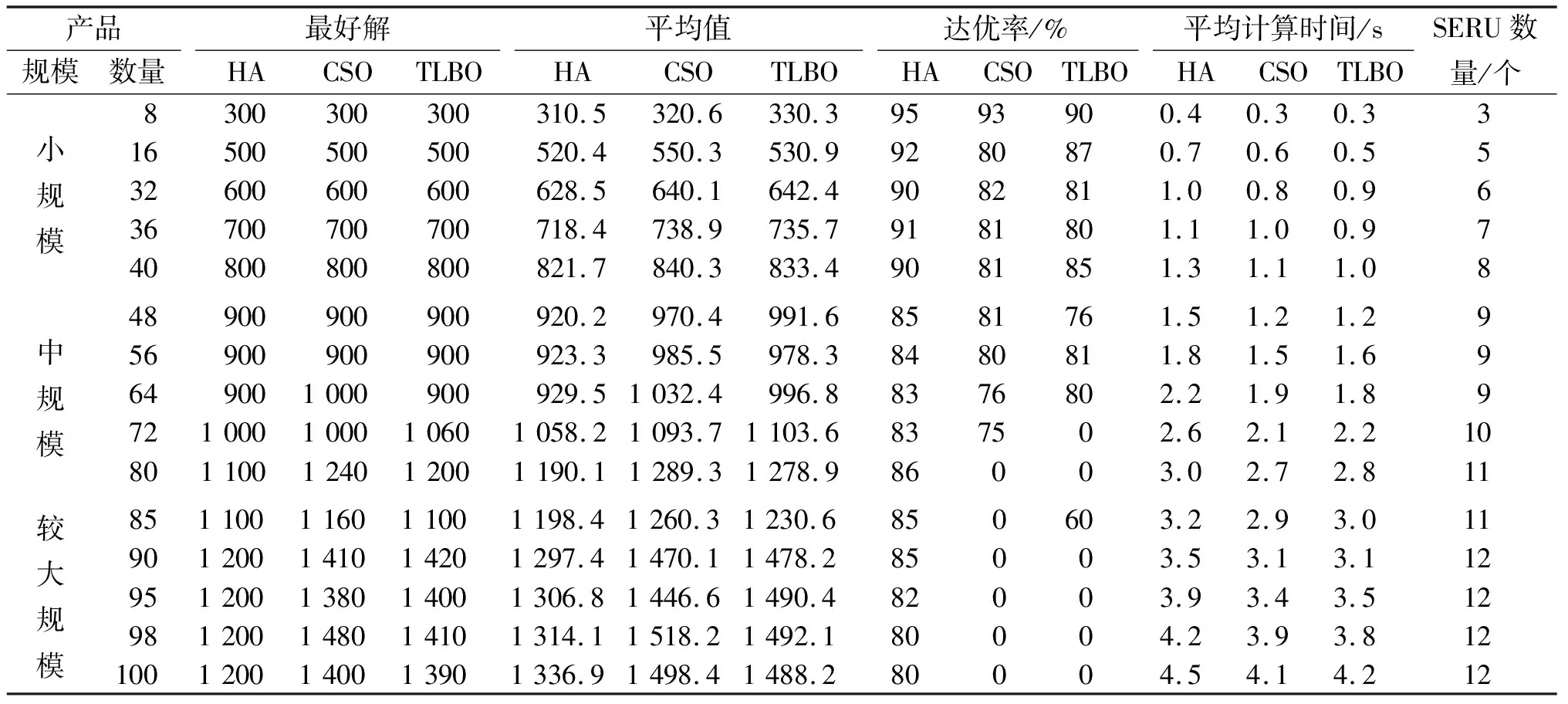
表4 混合鸡群-教与学算法(HA)计算性能比较表

因此，综合来看可以认为HA在大致相同的计算时间内取得的计算效果明显好于CSO和TLBO算法，针对SERU单元数量优化问题，HA不失为一种有效和适用的求解工具。

7 结 论

针对日本式单元生产系统中SERU数量优化问题进行了研究，提出了问题的数学模型，并结合国际上比较新颖的两类智能优化算法(CSO和TLBO)给出了问题的混合算法作为求解工具，取得了较为理想的效果。在后续的研究中，学者们可以考虑从问题复杂性入手，考虑多能工问题、车间调度理论以及库存和运输等相结合的集成优化问题，也可以考虑多个目标因素对问题的影响。从求解工具角度来看，可以考虑提出更加高效的编码方式和更加便捷、有效的新颖智能优化算法。