气动截止阀机理建模及其在阀门故障诊断中的应用
2020-04-09
(浙江工业大学 信息工程学院,浙江 杭州 310023)
气动截止阀作为核电站内使用数量较多的气动执行机构,主要用于主蒸汽系统的旁通阀、核取样系统的隔离阀、化容系统的下泄流孔板前后的隔离阀以及众多系统的安全壳外隔离阀[1]。就作用形式而言,主要分为气开式以及气关式,作用形式的选择主要受到工艺流程以及设备安全的影响。截止阀仅有全开以及全关两种位置状态,一般用于流体的快速截断以及开通,并不用于控制回路的调节,且开断时间是衡量其动作性能的重要指标。
目前,针对气动截止阀理论领域的研究较少,大部分研究主要集中于应用领域。如左修民[2]就气动截止阀的原理进行了分析并就气动截止阀的中性点设置进行了讨论;韩松等[3]就核电用气动截止阀执行机构的性能进行了结构设计以及检测;余美玲等[4]就气动截止阀开启时间超标的故障原因进行了分析。应用材料有限公司设计了一种手动气动组合截止阀,缩短了工艺流体控制装置的长度以及控制板的尺寸[5]。笔者建立了气动截止阀的机理模型,从理论上对其进一步深化,旨在为其后续的工业设计参数的确认以及选型奠定理论基础。
1 气动截止阀的机理建模
常见气动截止阀结构如图1所示,主要分为气动执行部分以及阀体。气动执行部分主体为薄膜气缸。手轮用于紧急状态下阀门的动作,中性点勺尺用于手轮位置的调整。气源入口与减压阀相连,用于控制压缩空气。气动执行部分通过联轴器与阀杆相连,由阀杆推动阀瓣动作。基本工作原理:以压缩仪表空气作为动力,通过DCS命令方式将动作指令发出,促使电磁阀开启提供动力给薄膜气室执行机构。在压缩空气的作用下,薄膜气室推动阀杆克服摩擦力以及弹簧弹力进行动作,进而带动阀芯动作,直到与阀座贴紧,实现对流体的开闭。
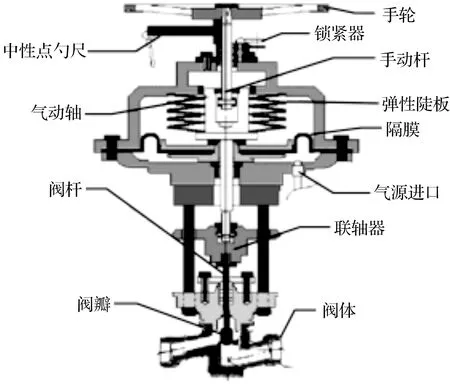
图1 气动截止阀结构图
基于气动截止阀的工作原理分析,将其机理模型分为两部分,分别为气动执行部分的质量流量模型以及阀体部分的动力学模型。
1.1 质量流量模型
将压缩空气经气动附件向薄膜气室充气的过程用收缩小孔流量特性进行等价。如图2所示,左侧为一理想气源,即压力不会随时间进行变化且内部空气流动速度u1约为0[6]。气源的气体密度为ρ1,压力为p1,温度为T1。右侧为小孔,其后假设为一空腔。设喷口出口处的有效截面积为Se,喷口处气体密度为ρ2,压力为p2,流速为u2,温度为T2。
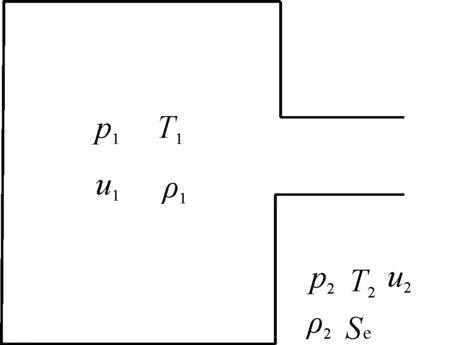
图2 小孔流量特性示意图
将空气视为理想气体,则其流动过程为一元等熵流动[7]。根据伯努利定理,有
(1)
则小孔处的流速u2为
(2)
式中k为空气比热容。小孔处的气体流速极快,可认为是绝热过程[8],即T1=T2。则流经小孔处气体的质量流量q为
(3)
式中R为空气的气体常数,且以上参数在一定工况下均为一定值。
假设小孔后连接为一密封罐体,且所有气动附件为理想附件,则当p1/p2大于0.528,小孔处气体的质量流量为一定值。此状态被称为声速流状态,此时气体质量流量的大小只与小孔处的等效面积相关。随着小孔后p2的压力上升,小孔处的质量流量减小。此时处于亚声速流状态时,质量流量不仅与开口面积相关,与小孔前后压差也相关。当处于声速流状态时,即其流量最大时有
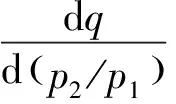
(4)
则其声速流下气体的质量流量为
(5)
再将声速流与亚声速流情况统一为θ的函数,即
(6)
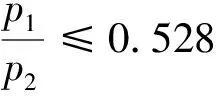
(7)
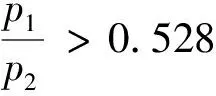
(8)
对于空气k=1.4,R=287 N·m/(kg·K),则声速流时θ为常数,即
(9)
亚声速流θ计算比较复杂,是压差的函数。当p1/p2>b时,根据标准ISO 6358所规定的亚声速流曲线,有
(10)
即将小孔的质量流量分为两种情况:
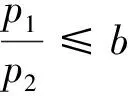
(11)
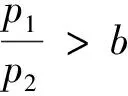
(12)
式中:q*为声速流时的质量流量;q为亚声速流时的质量流量;p1为小孔上游处的压力;p2为小孔下游处的压力;Se为小孔的等效面积;b为临界压力比。
由上述推导可以得出:气动附件的气体流量特性可以通过有效截面积Se以及临界压力比b两个特征参数进行描述。对于理想气体的流动,临界压里比b为0.528,但是由于在流速较大时,总参数与静参数之间存在误差,且在管道中存在压力损失,气动附件的b通常取0.2~0.5[9]。通过实验来确认气动附件的有效截面积Se以及临界压力比b后,利用式(11,12)可以描述在某时刻流入薄膜气室内压缩控制的质量流量qm。
1.2 动力学模型
由质量流量模型得某时刻的质量流量为qm,则此时薄膜气室内的压力P为
(13)
式中:R为气体常数;T2为薄膜气室的温度;V为此时刻的薄膜气室体积;qm为此时刻气体质量流量。
当气动截止阀处于动作状态时,在动作到某一位置时,主要受到薄膜气室在压缩空气作用下的气室压力,由薄膜气室压缩弹簧造成的弹簧弹力,由弹簧预压缩所带来的预紧力,由阀杆与填料以及其他部位摩擦所带来的摩擦力以及由阀芯上下不平衡面积造成的介质不平衡力。
阀杆受力情况[10-11]为
(14)
式中:M为阀芯以及阀杆的质量;x为开度位置;气室的压力Fa=AP,A为执行机构的膜片面积,P为气室气压;弹簧的弹力Fr=-kx;预紧力Fp=-kl,k为弹簧刚度,l为弹簧的预紧长度;Ff为阀杆所受的摩擦力;Fun为由于阀芯不平衡面积造成的不平衡力。
通过质量流量模型以及动力学模型的分析,得到模型的输入为:压缩空气气源压力;气动附件的有效截面积Se以及临界压力比b;气动截至阀本身的参数包括气动薄膜面积、弹簧刚度、摩擦力等;具体工况下介质压力作用于阀芯不平衡面积上的不平衡力。模型输出为阀门开度动作曲线。
2 实验验证
2.1 实验装置及方案
试验装置主要分为两部分,包括数据采集系统和实验对象。
数据采集系统以美国国家仪器仪表公司出品Crio-9030机箱为基础,搭载标准信号发射模块和标准信号采集模块,采集前端仪表所采集的气压以及开度信号。上位机以labVIEW为基础搭建上位机软件实现数据的处理。硬件采集装置如图3所示。

图3 实验采集装置
实验对象为浙江三方控制阀股份有限公司出品的两款阀:一款为气开阀,另一款为气关阀,并且分别在两种气源压力下做实验,得到4 组数据用于验证。阀门参数见表1。

表1 实验对象及其参数
为验证上述所建模型的准确性,搭建试验装置如图4所示。
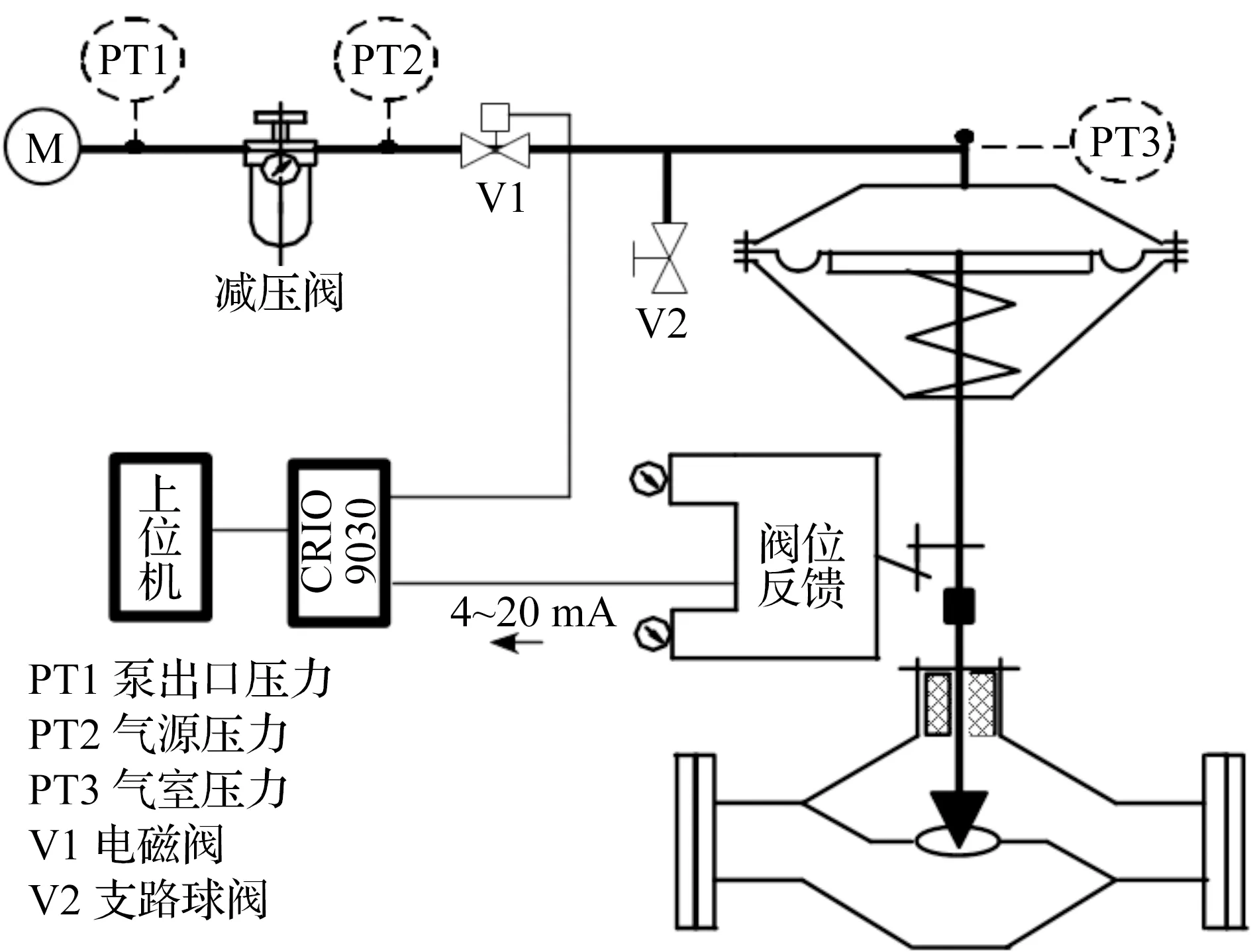
图4 实验装置示意图
实验步骤:1)搭建由稳压气罐、实验所用的管道和压力表等气动原件组成的试验装置,根据国际标准ISO 6358实验步骤测量气动部件的有效面积以及压力比阈值;2)连接试验装置,控制电磁阀对调节阀执行机构进行充气,同时记录气源压力以及调节阀的行程;3)调整气源压力,重复步骤2);4)更换实验对象,重复步骤2)及步骤3)。
根据国际标准ISO 6358所规定的方法测得所用气动附件的有效截面积Se,压力比阈值为b。实验测得有效截面积Se为6.89×10-6m2,压力比阈值为b为0.26。将气动附件参数,调节阀参数以及气源压力带入所搭建的simlink模型中。所搭建的模型如图5所示。
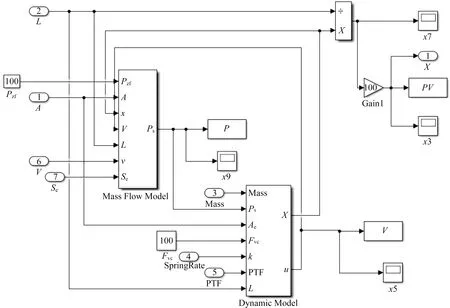
图5 模型图
2.2 实验结果
就两种气动截止阀分别在两种气源压力下进行实验,模型与实验的对比结果如图6~9所示。就所得的实验数据以及模型数据的差值进行误差分析,评价指标有均方根误差RMSE和平均绝对百分误差MAPE,如表2所示。从误差结果分析中可以看出:所搭建的模型与实验数据相比具有较高的相似性,说明所搭建的模型具有较高的仿真程度,可以较好地模拟真实的气动截止阀。
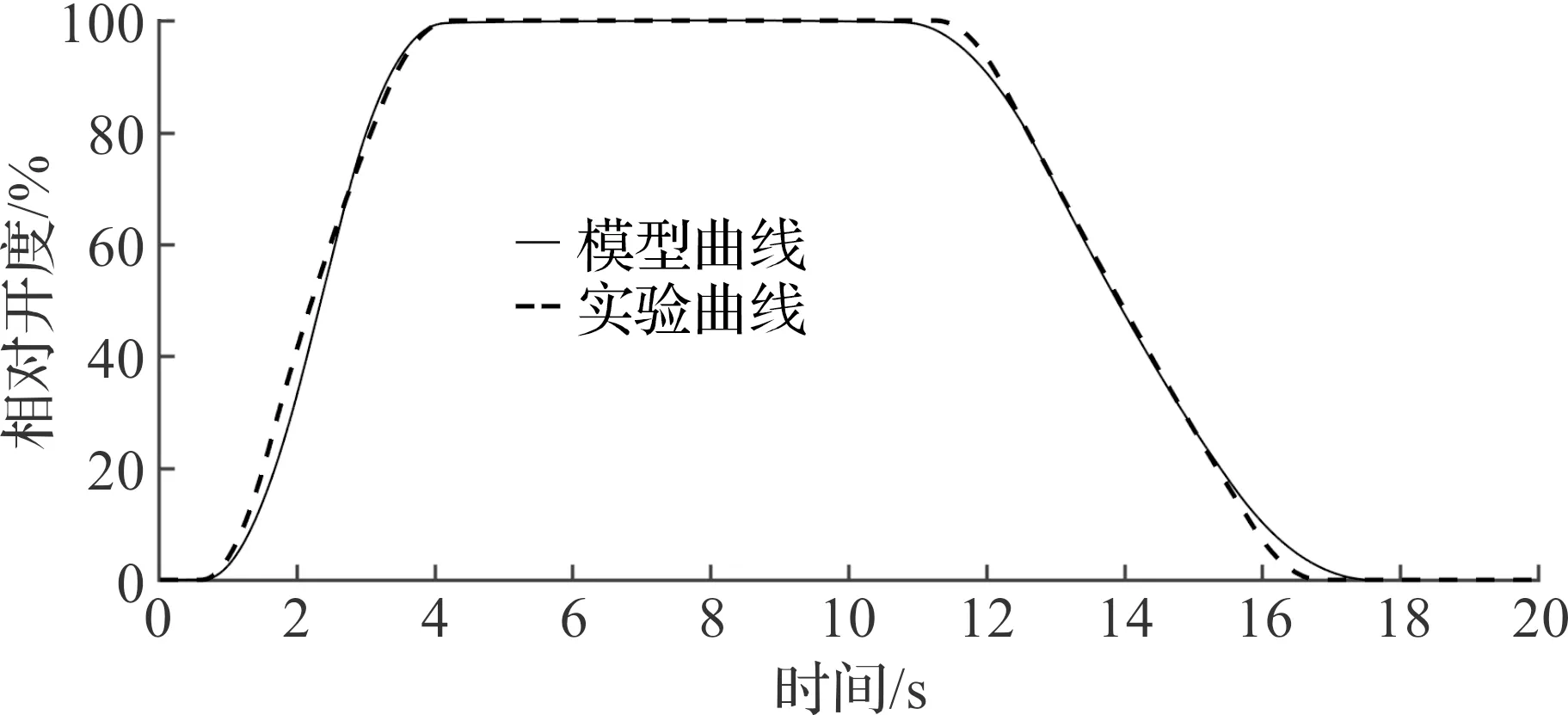
图6 A气动截止阀305.5 kP
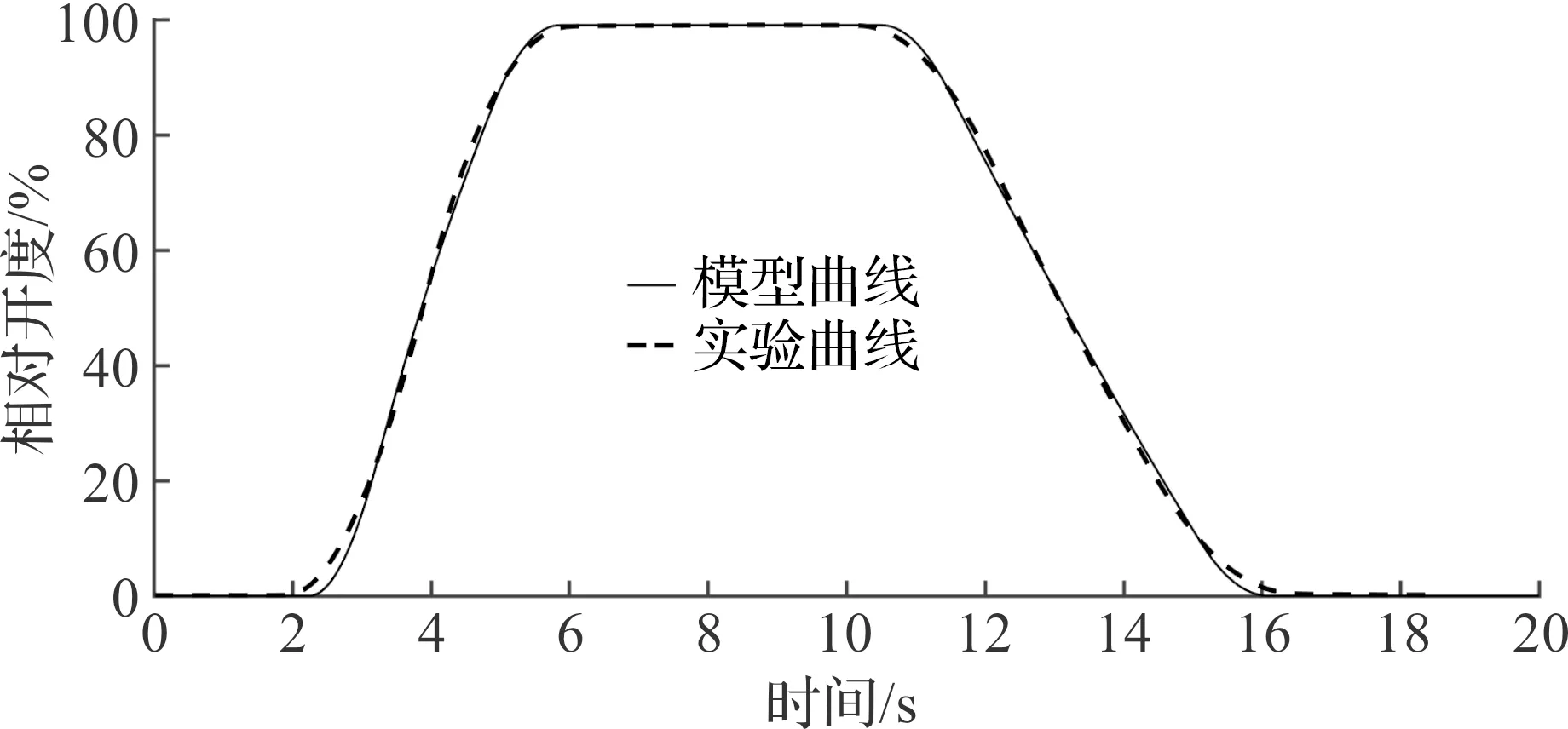
图7 A气动截止阀384.9 kP
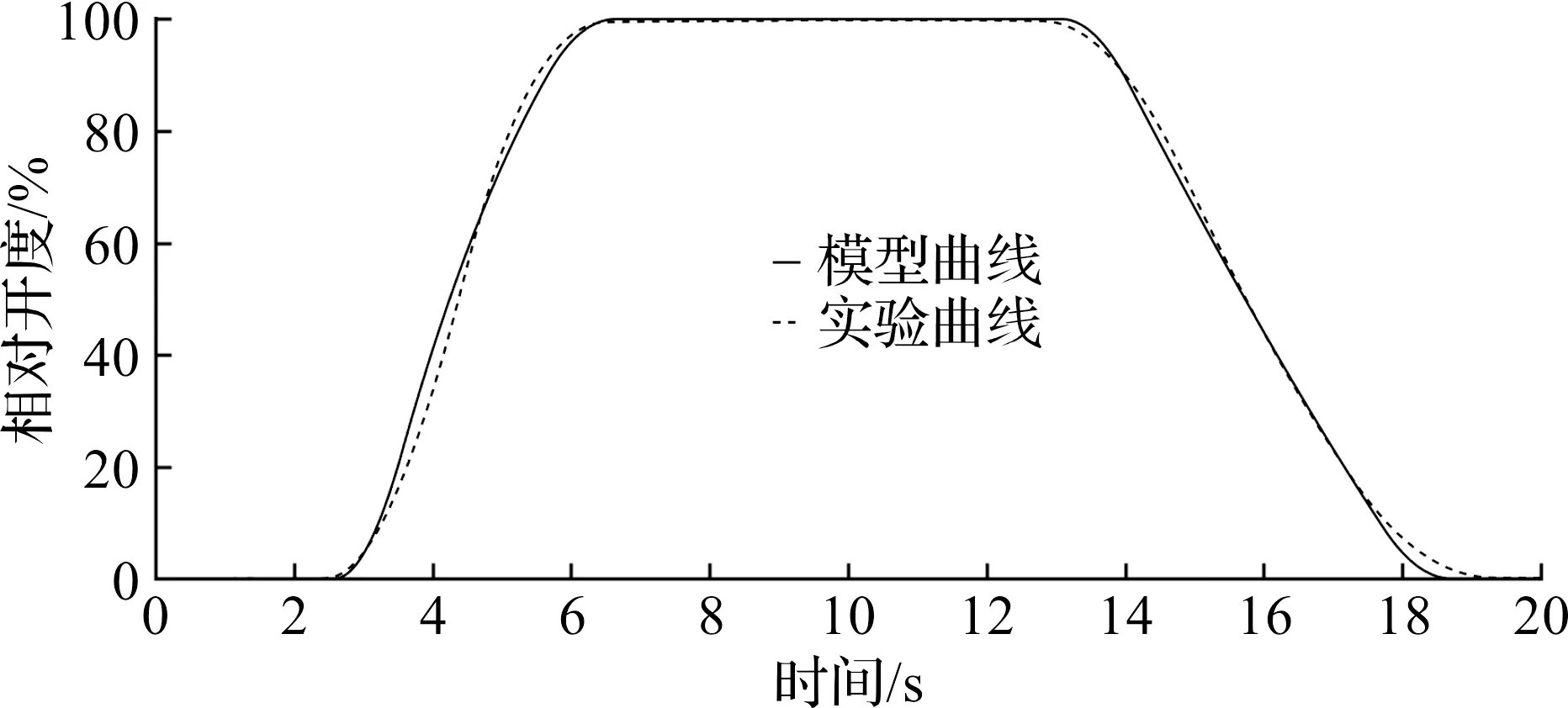
图8 B气动截止阀282.9 kP

图9 B气动截止阀384.8 kP
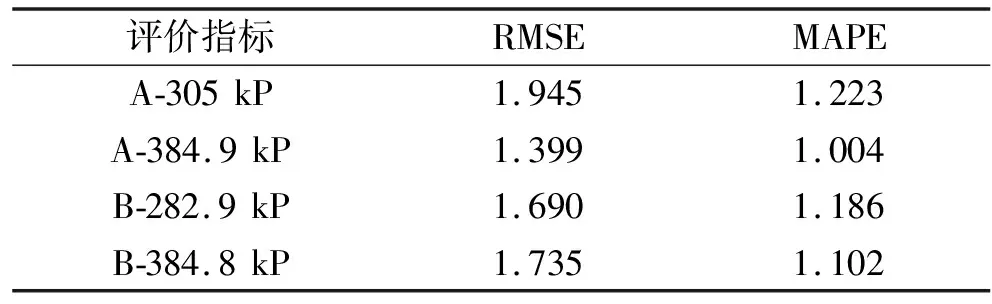
表2 误差分析结果
3 在故障诊断中的应用
气动截止阀作为过程控制回路的开断阀门,其动作时间是衡量其性能的重要指标。一般导致其动作时间减缓的原因较多。就气动附件而言主要包括:气源气压降低,且当小于某一压力时,阀不能完全开启;减压阀故障,减压阀出现漏气,导致压力波动,输入气室压力波动;管路故障,气动管路由于长时间使用导致出现老化裂缝,或出现较多凝结的水蒸气堵塞管路。就气动执行部分来讲,膜片以及气动接头的破损会造成动作时间变长。主要原因有:由于金属加工精度原因导致金属表面出现毛刺、尖角等缺陷,将膜片刺破;膜片长时间使用,导致材料老化强度降低,膜片表面出现孔洞;气路接口,因长时间使用以及压力原因导致接口松动等。就阀体而言,当填料与阀杆的摩擦力过大,也会造成动作时间减缓。
故障诊断方法可以分为三类:基于解析模型的方法、基于信号处理的方法以及基于知识的方法[12]。设计了一种基于模型的故障诊断方法,以模型作为气动截止阀动作时间的标定。当阀经过长时间的使用后,其动作时间会发生异常变化。以标定的动作时间为基础,当时间大于一阈值时,认定此阀出现了故障,需要进行维护。
实验方案:通过在气路增加一个支路,通过调节之路上通向大气的球阀的开度,模拟气路出现破损。实验方案示意图如图4所示。
实验结果分析:正常充气状态下在所搭建的模型上得到标定的响应曲线;通过调节旁通球阀的开度分别模拟弱漏气充气状态以及强漏气充气状态。如图10所示,随着故障强度即漏气量的增加,与模型对于动作时间的标定相比较得到:1)气动截止阀阀位由零至开始动作时间变长,即气动截止阀的响应速度降低;2)气动截止阀由开启动作至阀门全开时间变长,即全开启时间增加。由此两点得知该阀需要进行维护,就气密性易损部位进行排查。
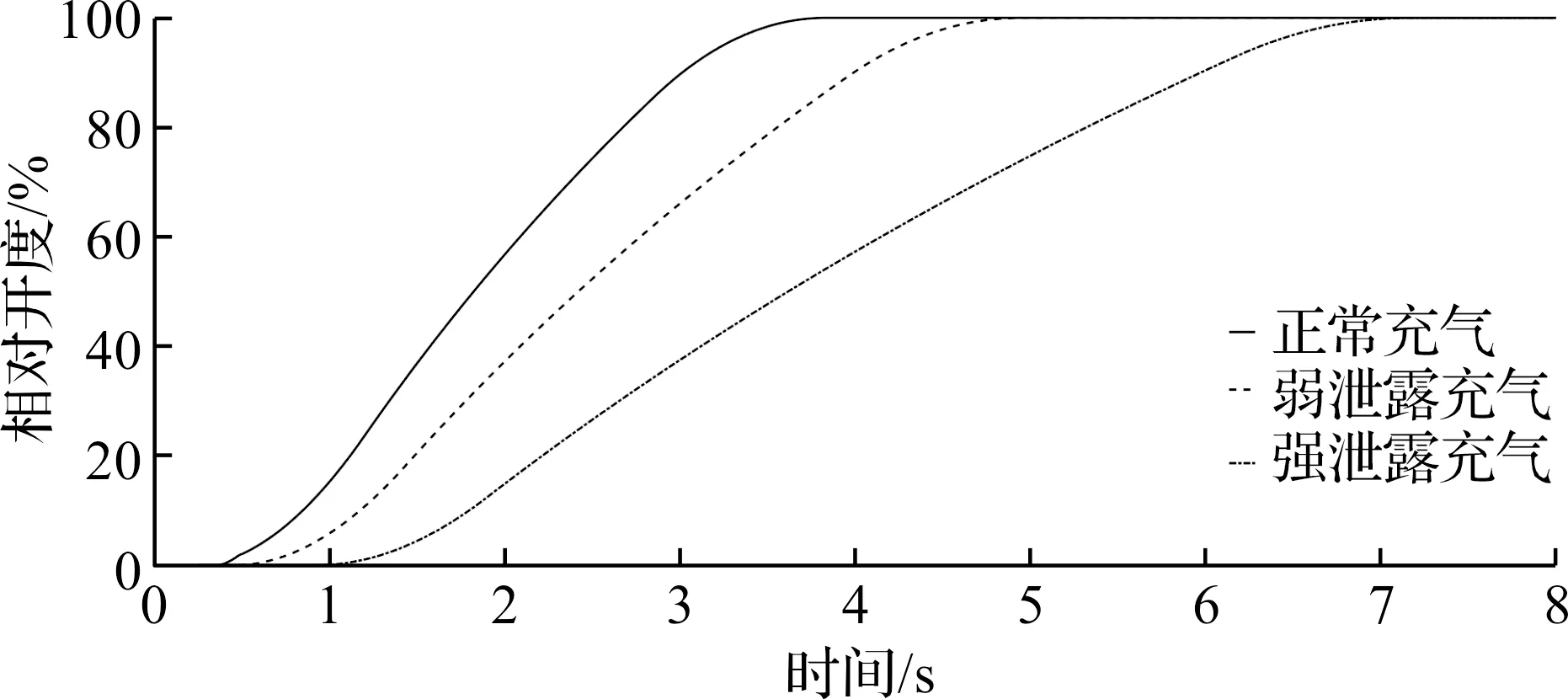
图10 故障现象图
4 结 论
建立了气动截止阀的质量流量模型和动力学模型。首先通过流体力学以及热力学原理建立了描述气动截止阀的质量流量模型,利用运动学原理建立了其运动学方程。两者结合,完整的建立了描述气动截止阀的动态模型。在此基础上,设计实验验证了模型,从RMSE和MAPE两个统计数据验证了模型的精度,证明了所建模型的有效性。最后设计了一种基于模型的气动截止阀气密性的故障诊断方法。
