微测井与方位加权插值精细近地表速度建模技术
2020-04-09金昌昆王延光尚新民崔庆辉王东凯
金昌昆 王延光 尚新民 崔庆辉 王东凯
(①中国石化胜利油田物探研究院,山东东营 257022; ②中国石化胜利油田博士后科研工作站,山东东营 257002; ③中国石化胜利油田分公司,山东东营 257000)
0 引言
近地表问题一直是陆上地震勘探的瓶颈。复杂近地表会严重影响地震波的激发和接收,并容易产生散射、次生干扰等噪声,淹没有效信号。近地表速度变化容易引起反射波同相轴畸变、振幅畸变,严重影响地震成像[1-3]。因此,研究近地表结构,尤其是近地表速度,一直是勘探领域的热点和难点。
近地表速度信息在地震数据采集前可通过近地表调查观测,在数据采集后可应用折射波解释[4-6]或初至层析反演[7-9]求取。现今常用近地表调查方法[10]有微测井调查、小折射法、浅层反射法、面波频散法[11-13]、地质雷达[14-15]、重磁电勘探[16]等。其中前两者最为常用,这两种方法各有特点,应用条件也有所不同。
小折射法主要适用于地形平坦、变化平缓的层状介质地区。而在地表地形起伏剧烈,低降速带速度和厚度横向变化大,高速层顶面不稳定,甚至速度发生倒转的复杂地区,小折射法往往难以适用。与小折射法不同,微测井的观测方式不受地形变化限制,施工中直接钻穿低降速带进行激发,接收的地震波信噪比较高,便于初至拾取。显然,微测井是一种相对成熟、可靠的近地表调查方法,即使是在巨厚砾石区,也能取得较满意成果。该方法的不足之处是成本较高,施工效率较低,通常仅在有限、离散的点展开[17]。若要得到完整的近地表模型,则要对离散数据进行内插,插值结果的精度取决于离散点的数量、分布和插值方法。插值的表层速度模型对地震数据现场采集、后期数据处理中的静校正、振幅补偿、深度成像[18]等具有十分重要的意义。
为构建精细近地表速度模型,本文提出一种基于微测井层析的方位加权插值建模方法,并在实际应用中与常规方法做了对比,结果令人满意。
1 微测井调查及插值建模简介
对于山前带等复杂地区的地震勘探,确定表层速度、厚度和最佳激发参数是十分重要的课题,而微测井调查发挥了举足轻重的作用。常规微测井调查首先钻穿低降速带,并从井底到井口依次布设激发震源,再由地面检波器接收透射波信号; 然后通过拾取初至走时并做垂直校正,得到垂向走时信息,绘制时深曲线。在地表速度呈层状分布的情况下,垂向走时分布具有一定规律性,同一地层内的垂向走时呈线性分布,而直线的斜率反映了地层慢度。根据这一规律,将时深曲线划分成不同地层并做拟合,计算出各层速度和厚度[19]。该解释过程可有效刻画局部速度结构,即使是在速度反转的情况下。但层位的划分通常依赖于处理人员的视觉和经验,参数选取的正确性和可靠性受人为因素影响,难以达到绝对准确、客观,尤其是在表层速度连续变化情况下,无法刻画层内速度变化,更易引入人为误差。
微测井调查获得的只是各点的垂向速度分布,若要描述完整的近地表速度分布,还必须进行数据内插。构建表层速度模型的常用方法有反距离加权法、径向基函数法、克里金插值法等[20]。反距离加权法效率高,能便捷地扩展到各向异性和高维情况; 但该方法对数据的分布较敏感,易出现“牛眼”效应。径向基函数法根据确定的基函数,构建线性方程组并求解加权系数。该方法插值效果好,但随着数据量增大,其计算量和储存量也显著增加,且求解过程可能出现不稳定问题。克里金插值是目前最常用的插值方法之一,该方法统计分析变差函数,并利用最小二乘算法求解插值系数。在插值过程中,采用的变差函数对插值结果的影响很大[18]。实际应用中,微测井观测点之间有较大间隔,实测数据欠充分均匀[21],直接拟合得到的变差函数可靠性较差。
为克服上述问题,通常基于数据统计特征和影响因素,选取适当的变差函数模型,再拟合确定其变程等参数。常用的变差函数模型有:高斯模型、指数模型、球形模型、幂函数模型等。若要描述更复杂的空间变异性,则需考虑尺度效应和各向异性情况,适宜的变差函数理论模型可描述不同尺度、不同方向的空间变异性。这需要大量的统计分析工作作为支撑,实际应用难度较大。此外,数据量较大时,求解克里金方程组也将变得困难。
2 微测井层析成像与方位加权插值
2.1 微测井层析成像原理
与微测井调查方法相同,初至波层析反演也是获取近地表速度分布的常用手段。它不依赖于层状模型假设,适用于复杂近地表情形; 对初始模型依赖性小,稳定性高,所得结果为地下各点的速度分布。微测井层析成像是一种将微测井的垂向走时、解释结果(地层厚度和速度)与初至波走时层析原理相结合,反演井壁速度分布的方法。
在图1中,假设微测井附近的地层速度横向变化可忽略,地震射线近似垂向传播,则可将实际三维问题简化为一维问题。以垂直校正后的初至走时作为观测走时T; 根据激发点、接收点的相对位置,计算垂向射线路径,并以各网格中的路径长度为元素,构建敏感度矩阵A; 设定井壁各点慢度值未知量为s,将微测井层位解释速度信息网格化,并以其倒数作为先验慢度值sH,则微测井层析的目标函数可表示为
(1)
式中:L为由一维二阶拉普拉斯算子构成的平滑矩阵;ε1为平滑约束权重;ε2为先验约束权重。引入单位矩阵I,与目标函数(式(1))对应的方程组为
(2)
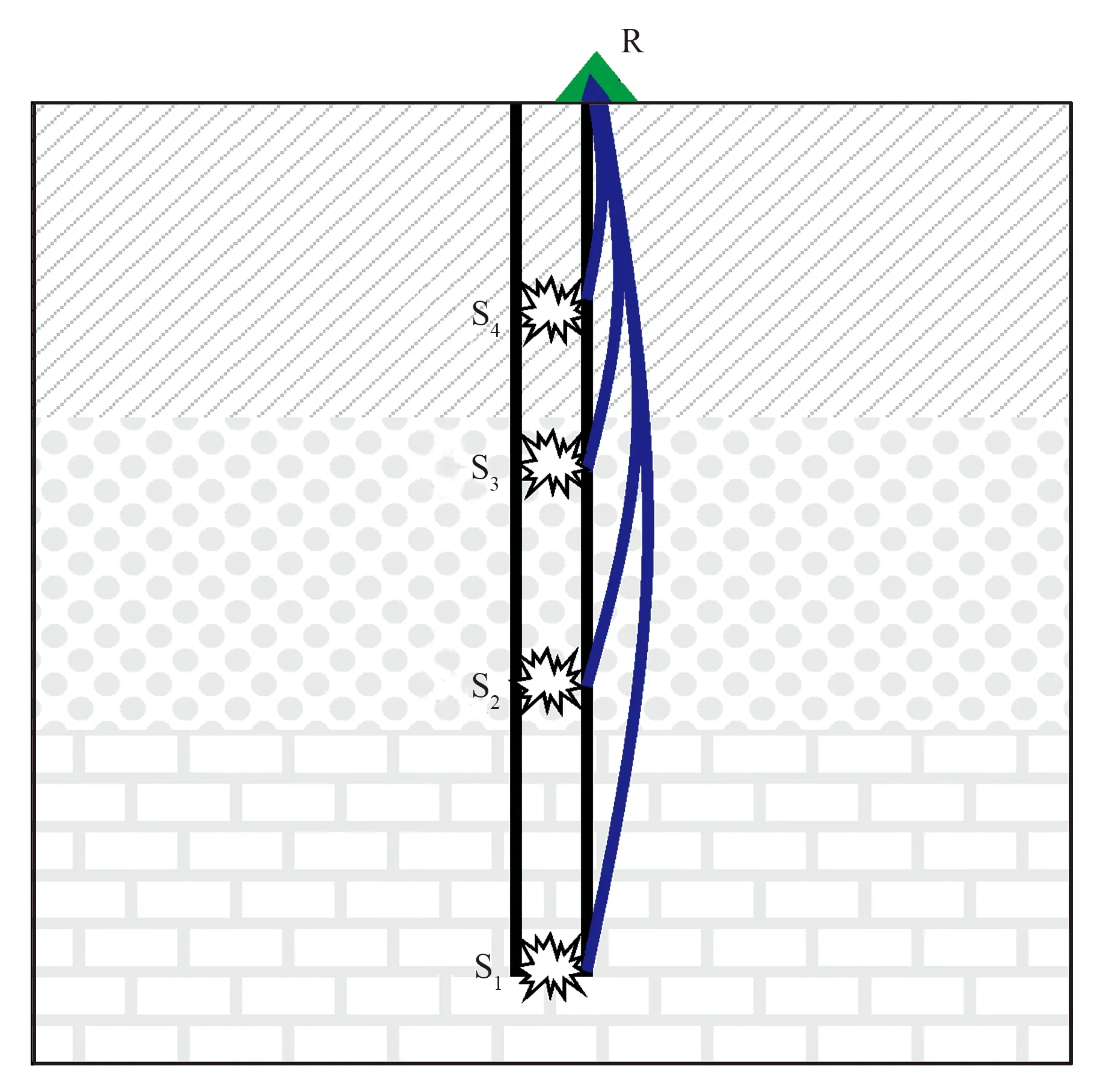
图1 微测井层析成像示意图
应用高效、稳定的联合迭代重建算法(SIRT)求解式(2),可得反演问题的最小二乘解。基于慢度值与速度值的倒数关系,慢度解可转化为井壁速度值。与常规初至走时层析反演不同,本方法射线路径及敏感度矩阵不随速度变化而改变,反演变量为井壁慢度值,而非慢度更新量。
以上处理将原问题转化为对线性反演问题求解,无须多次迭代,计算效率和反演稳定性高,可在微测井观测中进行现场处理。
2.2 方位加权插值
前已述及,微测井层析只能获得观测点处垂向速度分布,若要取得整个工区精细近地表速度场,就必须采用高精度横向插值方法。因此,本文提出一种基于微测井层析和层位信息并考虑方位因素的局部插值方法,以获得符合地表层趋势的精细模型。该方法主要涉及三个方面:基于层位的深度变换、构建基函数及求解权重方程组。
2.2.1 基于层位的深度变换
常规插值方法只考虑距离因素,且结果带有明显的平滑效应,而近地表往往是速度变化最剧烈的区域,横纵向变化十分明显。在地表层位起伏情况下,做横向插值所用数据可能来自不同速度的地层,若不做区分直接进行插值,其平滑效应会使插值结果产生横向拉伸现象。
为避免此情形,本文在插值前对微测井数据进行基于层位信息的深度变换,将沿起伏层位的数据转化为沿水平分布的数据,横向插值采用来自同一地层、同一深度的数据,插值完成后将沿水平分布数据反变换为沿起伏层位数据,可减少拉伸效应,并使插值结果符合层位趋势。有如下具体步骤。
(1)基于微测井解释的地层信息,通过反距离加权计算得到地下界面。
(2)以各界面的平均深度为基准,对微测井速度所对应的深度进行标准化,变换公式为
(3)
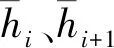
2.2.2 构建基函数
数据的空间相关性是空间插值研究的基础。Tobler定理认为空间上距离较近的数据比距离较远的数据具有更大的相关性[22],反距离加权、克里金插值等方法均服从这一定理。另外,数据在不同方向上可呈现出不同的变化,所以数据的空间相关性也具有各向异性特征[23]。因此,不同方向、相同距离上的数据对插值点的权重也应有所不同。为表征不同距离、不同方向的权重,本文构建的权重基函数包括径向基函数和方位基函数。
径向基函数:与全局径向基函数法不同,本文方法为一种局部插值方法,将凸起的余弦函数(汉宁窗)作为径向基函数,以降低计算量和存储量,并保证插值精度。基函数的具体形式[24]为
(4)
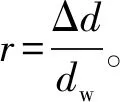
方位基函数:本文以八个主方位系数(正北、东北、正东、东南、正南、西南、正西、西北)加权结果表示各个方位权重。每个主方位的加权函数为二阶三角B样条函数,其分段表示形式[25]如下
(5)
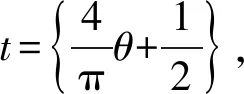
(6)
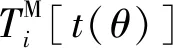
图2b显示八个主方位的B样条函数曲线在极坐标系下的分布,各主方位系数[0.8,0.8,0.8,0.8,0.4,0.4,0.8,0.8]的插值曲线(图2c)展示出相应的各向异性特征。
式(6)中B(θ)无法给出(θ,r=0)处的权重值。为此,将插值函数B(θ)进一步修改,作为方位基函数
(7)



图2 方位基函数显示图
(a)主方位B样条曲线; (b)极坐标系中八个主方位B样条曲线分布; (c)方位系数[0.8,0.8,0.8,0.8,0.4,0.4,0.8,0.8]在全方位上的插值结果(方位顺序依次为正北、东北、正东、东南、正南、西南、正西、西北); (d)与图c对应的方位基函数在定义域中分布显示(c=0.1)
基于式(4)与式(7),本文方法采用两者乘积的形式作为权重基函数
(8)
通过以上方法构建的权重基函数具有紧支撑性和各向异性特征。
2.2.3 求解权重方程组
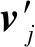
(9)
式中:vi为第i口井速度;W(θij,rij)为权重基函数;B(θij)为基于方位角θij的插值函数;θij、rij、Rij分别为第i口井到第j口井的方位角、距离参数和径向权重;wik为第i口井的第k个主方位系数。
将式(6)代入式(9)得
(10)

基于式(10),建立如下插值目标函数
(11)
式中:敏感度矩阵G的元素为由式(10)中与主方位系数相乘的系数值; 微测井的主方位系数w为未知量;V为微测井层析速度; 平滑矩阵L由微测井相邻主方位系数之间的平滑约束项构成;ε为平滑权重系数。与式(11)对应的反演方程组为
(12)
应用最小平方QR分解算法(LSQR)求解上述方程组,得到各微测井的主方位系数。与各向异性克里金插值统计区域各向异性不同,本文方法通过反演计算每口微测井相关性的各向异性特征。基于求解的主方位系数,插值点p的计算结果可表示为
(13)

3 实际应用
3.1 准南缘地区激发井深设计
中国西部探区大多具有地表及地下地质构造“双重”复杂介质特征[26]。准南缘米泉区块位于博格达山西北缘,地势西北低、东南高,地表高差达3km,为典型的山前带地貌[27-28]。工区北部低缓丘陵区分布有黄土、巨厚砾石层,南部山区出露二叠系灰质细砂岩或石炭系灰岩,中部高大丘陵区为侏罗系细砂岩和煤层。此次近地表调查采用了微测井、浅层地震等多种技术手段,其中微测井调查共173口,有5口为100m以上深井微测井,用以查明巨厚砾石层的底界。
图3展示了该地区微测井的解释结果和层析结果,包括微测井的时深曲线及层位解释(图3a)、微测井层析成像反演结果(图3b)。对比两者可见,微测井解释的斜率与时深曲线并不完全吻合,而层析结果却能清晰地展示地下速度变化细节,包括地表速度反转。
三维地震施工前,为确定不同地表条件下激发井深等设计参数,在工区内设计了自西北到东南的4个激发试验点。其中,S1试验点位于黄土砾石区,钻井深度达100m,未钻穿砾石层。图4a为S1点的微测井层析速度曲线,可见井壁速度整体在2.5km/s以下。S2试验点位于工区中北部,钻井井深为26m,从该点的微测井层析速度曲线(图4b)可见:在井深20m之下为3~4km/s的高速层,实际钻遇地层为侏罗系细砂岩。S3试验点位于工区中部,钻井井深为50m,从该点的微测井层析速度曲线(图4c)可见,深部高速层为侏罗系细砂岩,浅部低速为表层土、黄土及砂砾层。S4试验点位于工区中南部,钻井井深为22m,从该点的微测井层析速度曲线(图4d)可知:浅层速度低,主要成分为表层土和被风化的松散岩层; 深层速度在3~4km/s之间,为二叠系灰质细砂岩。米泉勘探通过各试验点的微测井调查以及大量的激发接收试验,明确了激发井深与激发岩性、激发速度的关系,确定了不同地表岩性条件下的最佳激发参数和激发原则,进而完成了逐点激发井深设计任务[29]。
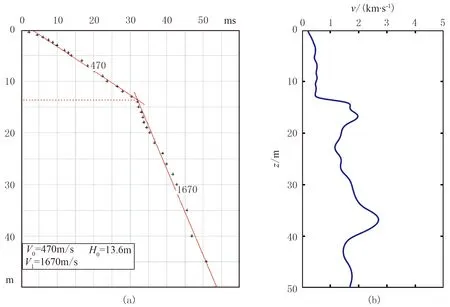
图3 米泉微测井解释结果(a)与层析结果(b)对比
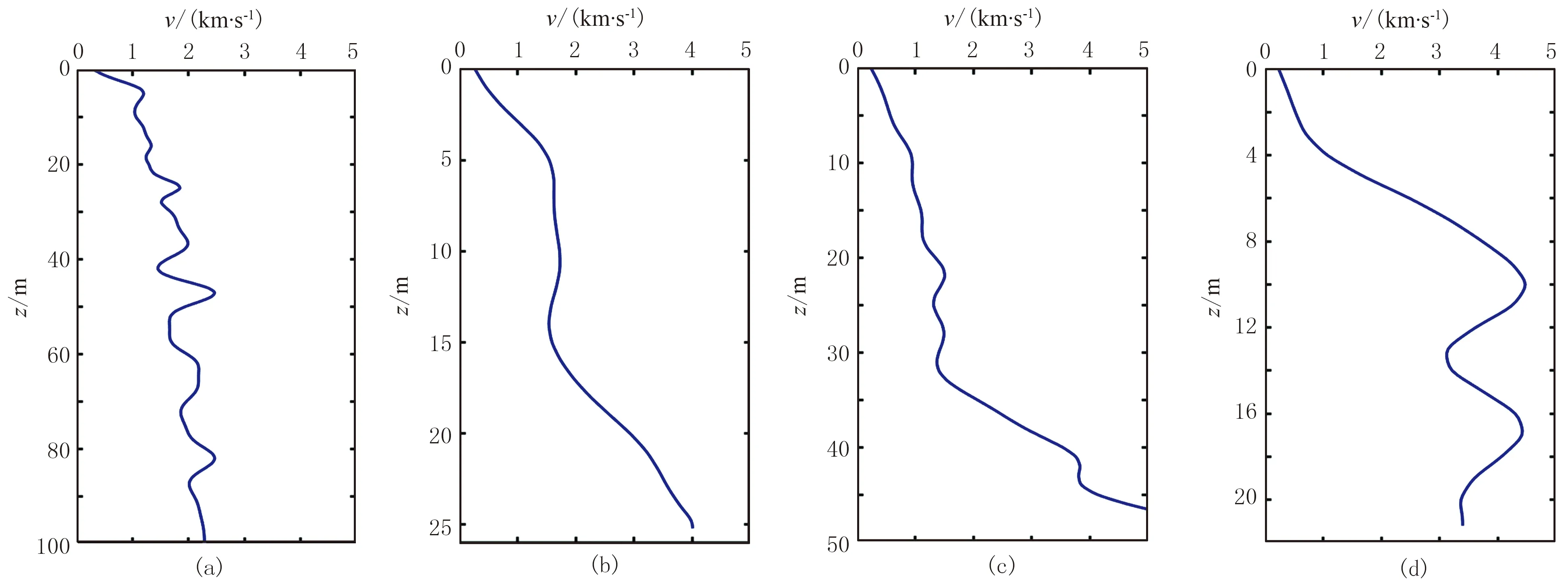
图4 试验点的微测井层析反演结果
3.2 陈官庄地区精细表层建模
陈官庄地区位于济阳坳陷,地表为第四系沉积物,潜水面浅,低降速带稳定,变化平缓,但仍存在异常区域。该区共做微测井129口,平面分布如图5a所示,微测井间距约为2km,钻井深度不超过30m,井壁速度不超过2km/s,钻遇地层以胶泥层为主,微测井解释结果(图5b)和层析速度曲线(图5c)均具有清晰的层位特征,层内速度较稳定。
根据速度曲线特征,工区近地表可划分为三层:第一层速度在0.6km/s 以下;第二层速度约为1km/s;第三层速度在1.4km/s以上。基于微测井的解释层位,插值得到全区层位分布(图6a)所示。对微测井数据做深度转换,并以4km作为最大井间距做方位加权插值,获得最终反变换后结果(图6b),可见该插值速度与层位趋势(图6a)相符合。
作为对比,采用普通克里金法进行插值。由于微测井分布稀疏,计算变差函数时采用各向同性模型表示。通过分析、拟合,以趋势相符的线性模型作为理论变差函数模型并得到变程、基台值、块金常数等参数。之后基于无偏性和最小二乘原理,利用拉格朗日乘法构造目标函数,并求导得到克里金方程组,求解得到插值权重,进而得到插值模型。
图7为两种插值结果的速度切片(深度为6m)。总体而言,两种方法的插值效果基本相当; 但对比黑色方框部分可知,本文方法结果(图7b)比普通克里金法(图7a)具有更高的横向分辨率。
为测试插值结果的准确性,以横向距离为14.09km、纵向距离为6.113km处的微测井数据作为验证数据,得到如图8a所示的解释结果。基于其他微测井的层位及速度信息,应用本文方法和普通克里金法对待验证位置做插值处理。从插值结果与验证数据的对比(图8b)可见:当深度小于10m时,两种结果与验证数据具有较高的吻合度,而在2.16m和8.34m处速度界面附近,本文方法结果的纵向分辨率高于克里金插值结果,更符合验证数据; 当深度大于10m时,两种插值结果的变化平缓,虽未体现出验证数据的局部异常,但在趋势上与验证数据一致,证明了插值结果的准确性。
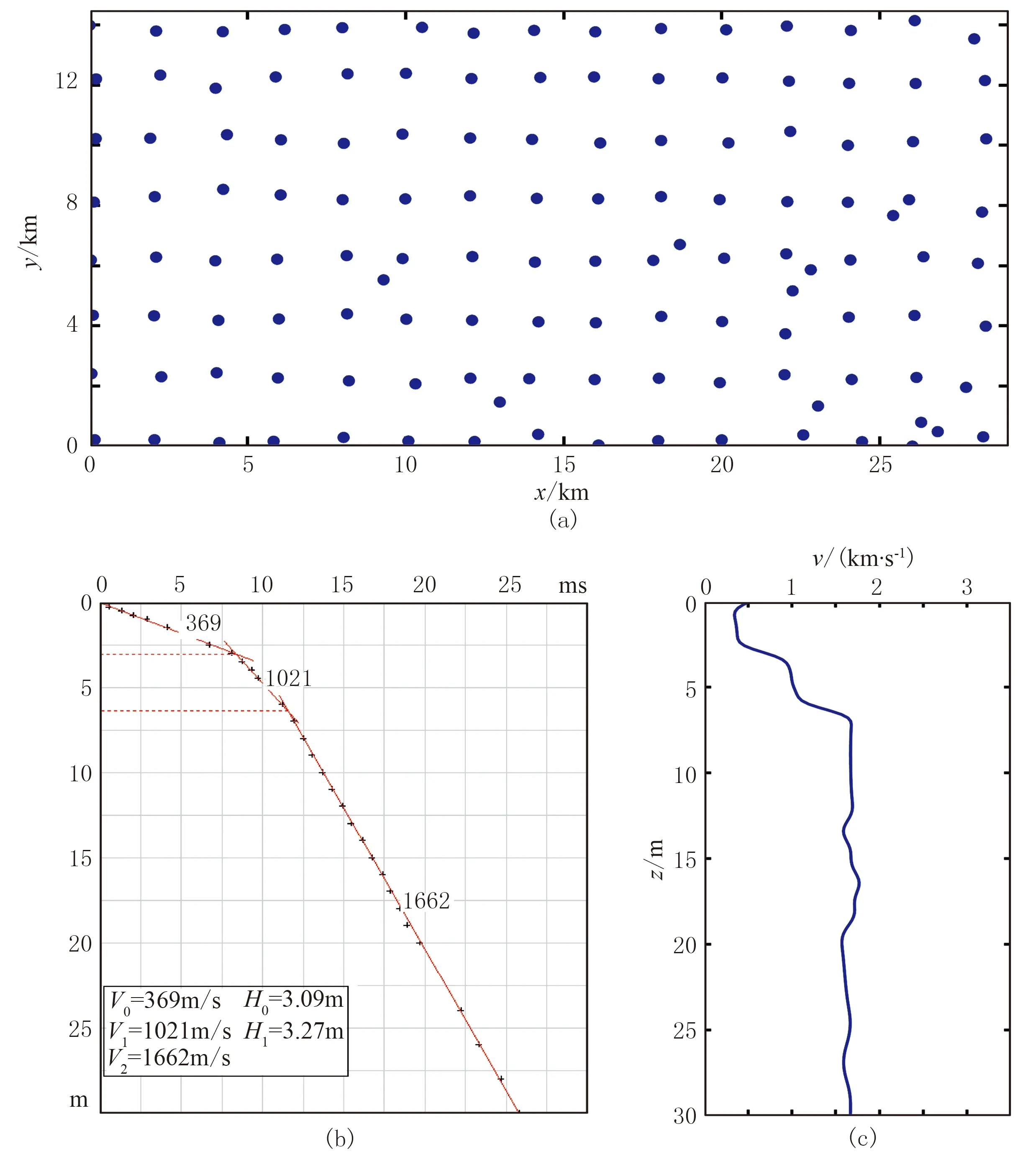
图5 陈官庄地区微测井调查情况
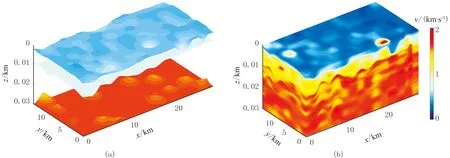
图6 陈官庄地区近地表层位分布(a)及插值结果(b)

图7 普通克里金法(a)与本文方法(b)的速度切片对比
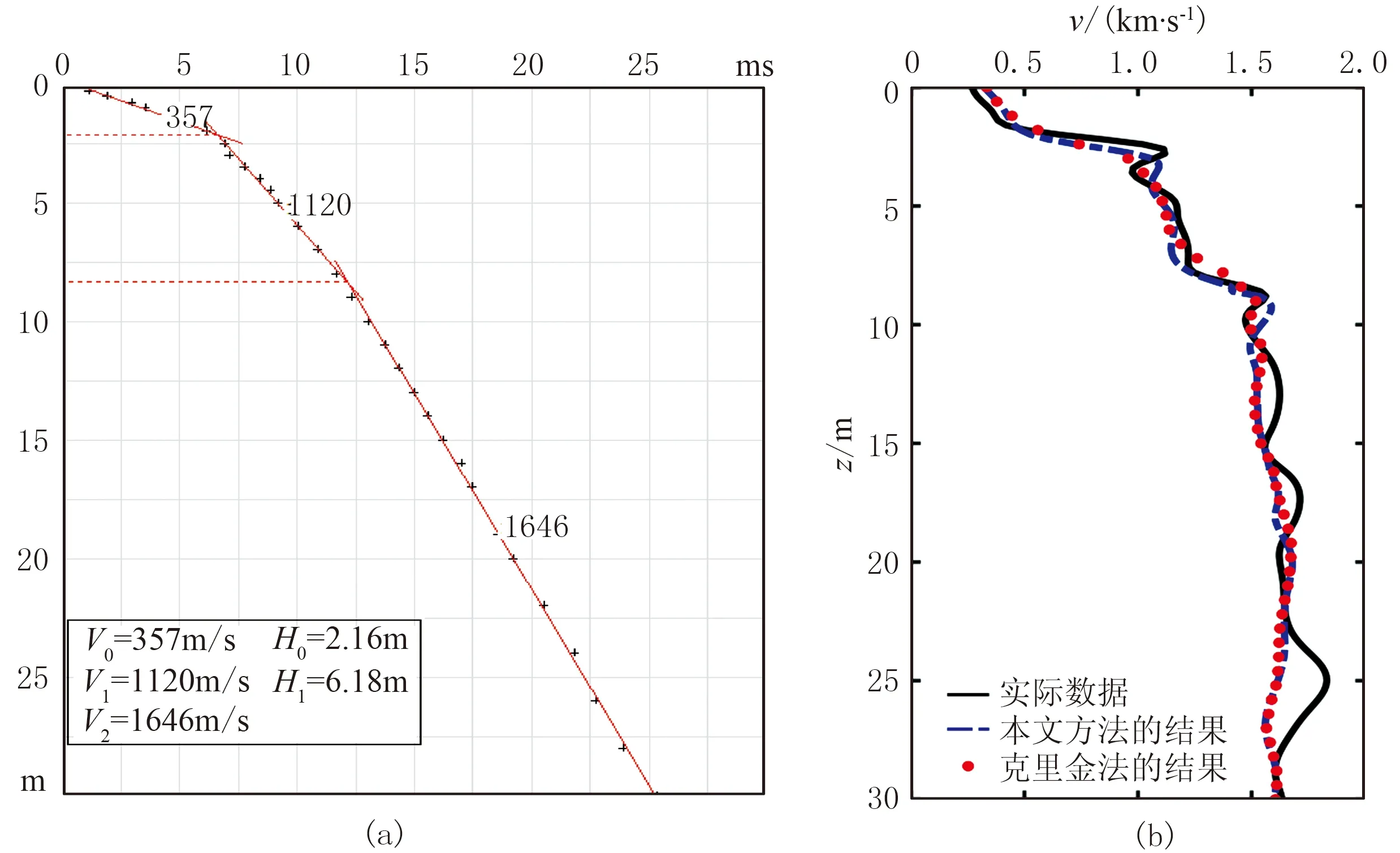
图8 验证数据与插值结果显示图
4 结束语
本文提出一种基于微测井层析的方位加权插值建模方法,实际数据测试结果表明:
(1)与常规微测井解释相比,文中的微测井层析成像可获得更精细、连续的井壁速度分布;
(2)该方法反演微测井的主方位权重,无须人工进行各方位的数据统计与分析,方便快捷; 所得速度数据符合层位趋势,且纵横向分辨率局部优于普通克里金插值的结果。
