基于物品的统一推荐模型
2020-04-09黄佳进
邓 凯,黄佳进,秦 进
(1.贵州大学计算机科学与技术学院,贵阳550025;2.北京工业大学国际WIC研究院,北京100000)
0 引言
推荐系统旨在为用户提供需要的物品,让用户能更快速更高效地找到自己所需物品。在信息过载的时代,推荐系统在电子商务、音乐/电影/书籍网址、社交平台等许多网络服务上扮演着重要的角色。现如今推荐系统已经成为了人们研究的热点话题,并且在信息检索、人工智能以及数据挖掘方面的关注度在逐渐增加。
在各种推荐方法中,协同过滤(Collaborative Filtering,CF)[1]已被人们广泛采用,它通过用户与物品之间交互的数据来预测用户与物品间的相关性。在一种假设下:CF 通过给相似用户推荐其他用户喜欢的内容;另一种假设是:基于用户对物品的偏好找到相似的物品,然后根据用户的历史偏好,推荐相似的物品给他。根据不同的假设,CF 被分为两种类型:一种是基于用户的协同过滤方法(User-based Collaborative Filtering,UCF);一种是基于物品的协同过滤方法(Item-based Collaborative Filtering,ICF)[2]。矩阵分解(Matrix Factorization,MF)模型[3-4]在UCF 中是一个典型的例子,通过计算该用户的潜在因子(Latent Factor,LF)和对应物品的LF的内积,最后将内积的结果作为预测的评分矩阵。基于物品的协同过滤表示一个用户已经购买过的物品记录,并且通过使用该用户要购买的目标物品和该用户购买过的物品的相似性来评估用户-物品的相关性。为了更好地表示出一个用户和他购买过的物品记录,每一个用户都有一个固定的ID,这样在输入阶段ICF过滤方法与UCF 相比更具有标志性。此外,当一个用户有新的物品购买记录或者一个新用户开始购买物品,不需要重新训练模型参数来更新推荐列表。ICF 能通过简单的检索新购买的物品和之前购买过的物品的相似性来更新物品清单。然而UCF 方法像矩阵分解一样将模型参数与用户ID 关联,强制它们为了一个用户更新参数来更新推荐列表(MF是在线更新策略)。
在最近几年,用户购买的物品被应用在两种常见的代表方法中:一种是直接采用用户已经购买过的物品作为输入向量,并且采用神经网络把输入的向量转化为能更好表示用户低秩表示的学习(Latent Low-Rank Representation,LatLLR),这充分利用了神经网络的非线性和高容量特征;另一种表示将每一个被用户购买过的物品作为一个潜在向量,并且把这些潜在向量两两内积计算其两个物品的相似性。前一种方法仅仅是把历史物品转化为一个用户向量而没有考虑物品之间的相似性;后一种方法考虑了物品之间的相似性,但每一个被购买过的物品都有很多参数以及一个额外的潜在向量。因此这两种方法各有优势,如果能把这些不同性能的方法整合起来将得到更好的推荐效果。
1 相关工作
虽然MF 在推荐研究中很受欢迎,但ICF 在推荐系统中效果要好于UCF。ICF 通过表示用户所购买的物品,在物品中编码更多的信号输入,并不是简单地使用ID 表示用户的UCF。这为ICF 提供了更大的潜力,且提高了用户偏好建模的准确性和可解释性。对于top-N 推荐,ICF 方法的准确性优于UCF 方法[5]。ICF 可以将推荐的物品解释为与用户之前购买过的某些物品高度相似,这比基于“相似用户”的解释方案[6]更容易被用户接受。其次,ICF在用户偏好建模中的可组合性使得在线个性化[7]的实现更加容易。例如,当用户有新的购买时,ICF 不需要重新训练模型参数来刷新推荐列表,而只需检索与新购买的物品相似的物品,就可以近似地得到已刷新的列表。这种策略基于用户最近的观看成功地在YouTube 上提供了即时个性化。相比之下,像MF 这样的UCF方法将模型参数与用户ID 关联起来,使得它们必须更新模型参数来刷新用户的推荐列表。
ICF通常是采用Pearson相关性和余弦相似度来计算两个物品之间的相似性[8-9]。近年来,为了从数据中学习物品相似度,人们研究了获取数据特征的方法,其中比较有代表性的两种方法是稀疏线性方法(Sparse Linear Method,SLIM)[10]和分解物品相似度模型(Factored Item Similarity Model,FISM)[11]。在FISM 中,两个物品之间的相似性是通过它们的潜在向量乘积后得到的,可以将其视为物品-物品相似矩阵。ICF 的一些最新发现通过神经注意相似度(Neural Attentive Item Similarity,NAIS)模型扩展了FISM 模型。利用注意网络区分物品间的相似性对预测更为重要,即协同去噪自动编码器(Collaborative Denoising Auto-Encoder,CDAE)[12]采用非线性自编码结构[13]学习物品相似性全局和本地SLIM,它为不同的用户子集使用不同的SLIM模型。
MLP(Multi-Layer Perception)[1]是一个多层神经网络模型,它一般由三部分组成:一部分是输出层且含有多个感知单元;一部分是由多个感知单元构成的一层或者多层隐藏层;还有一部分是含有多个感知单元的的输出层。MLP被广泛地应用于自然语言处理、图像处理等多个领域。在本文工作中,将MLP 应用于个性化推荐领域,用于建模用户和物品或者是物品与物品之间的交互关系。
基于前人的研究,本文将FISM 模型和MLP 模型结合成UICF模型,这对于物品的推荐更具有表征力。
2 模型设计和描述
2.1 MLP
设用户集U 包含M 个用户,物品集I 包含N 个物品,ruj表示用户u 对物品j 是否有过交互。对于隐式反馈(如购买),ruj用二进制数1或0表示用户u是否和物品j有过交互,1表示有过交互,0 表示没有。这种思想是基于物品的协同过滤,它通过一个用户和该用户在过去所有交互过的物品与现有物品i的相似性来预测该用户对现有物品i的偏好。
对于用户u 有:ru=(ru1,ru2,…,ruN)。本文把一个N 行N列的物品-物品表示为相似矩阵S。在相似矩阵S 中第i 行和第j 列表示的是第i 个物品和第j 个物品的相似性。Si表示的是物品i 和其他所有物品之间的相似性。的值表示的是用户打算购买的目标物品与该用户之前交互过物品的相似性。预测模型被表示为:
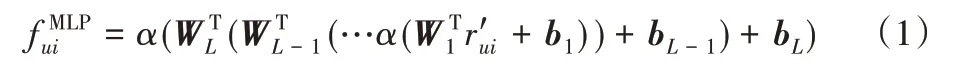
其中:W*和b*表示每一层的权重和偏置,α 是Sigmoid 激活函数。
2.2 FISM
Ru表示用户u 购买过的物品集,并且每一个物品被两个嵌入向量p 和q 划分为两部分:一部分是预测的目标物品,另一部分是之前与用户交互过的物品。预测模型表示为:

式(1)采用0-1 向量直接表示一个用户的输入,并且把这个向量转化成一个LatLLR 方法。两个向量的内积被直接用来表示物品i与购买物品i的这个用户之前所交互过的所有物品之间的相似性。在式(2)中,被购买过的物品嵌入到q ∈RN×d中,其中d 是物品嵌入的维度。式(2)能被考虑作为计算物品i与购买物品i的用户所有交互过的物品之间相似性的一种直接方法。不同的0-1 表示,不仅从整个物品集中获取物品的嵌入,并且这样还包含了全局语义信息。对于每一个被购买的物品,这样的分布式表示自然可以作为用户对物品的喜好程度。
2.3 MLP和FISM结合
为了结合FISM和MLP这两种模型,本文需要设计一种策略融合它们,以便结合后它们的性能都得到增强。其中一种最常见的融合策略是通过连接学习表示法来获得联合表示,并且把这种表示输入到一个全连接层。在本文的方法中,预测函数是由两步得到的:第一步,该模型利用FISM 模型和MLP 模型中用户偏好潜在因子和物品潜在因子的元素乘积⊙分别计算出两个预测向量;第二步,将用户进行Multi-Hot编码,目标物品进行One-Hot 编码,再用不同权重将两个预测向量串联起来。CF 两种类型方法有不同的优势,并且从不同的环境中学习预测向量,将这两个预测向量连接起来,将得到一个更健壮、更鲁棒的联合表示用户-物品对。由此产生的全连接层使模型能够对联合表示中包含的特征分配不同的权重。图1说明了上述提出的融合策略,给出的形式如下:

其中:hT、b 分别是权重和偏置,σ 是Sigmoid 激活函数。UICF的模型图如图1所示。
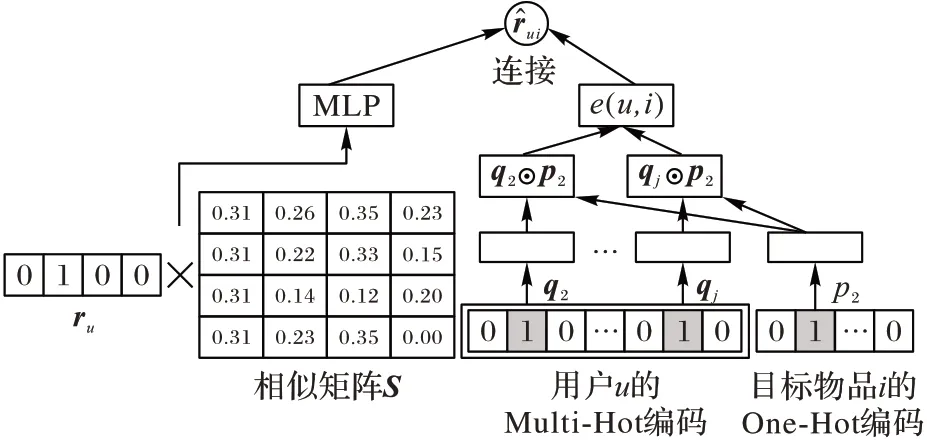
图1 UICF模型Fig.1 Model graph of UICF
2.4 损失函数
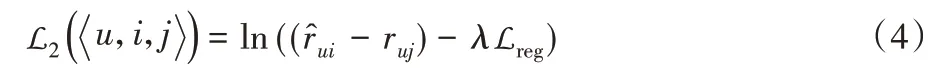
其中σ 是Sigmoid 函数。Sigmoid 函数是一个单调增函数,在式(4)中将使得大于
文献[14]提出,模型参数的初始化对基于深度学习(Deep Learning,DL)的模型收敛和最终表现起到相当重要的作用。为了能够得到更好的预测评分的效果,先初始化FISM模型的参数,使其服从均值为0、标准差为0.01 的Gaussian 分布,然后再训练FISM 模型直到收敛。同样地,也初始化MLP模型,使其服从均值为0、标准差为0.01 的Gaussian 分布。对于最终模型的融合是分别将单独训练好的FISM 模型和MLP模型对应参数初始化融合模型中的FISM 和MLP,其中包含了FISM 中的用户偏置项、物品偏置项以及MLP部分隐藏层权重系数和偏置项的初始化。
3 实验结果与分析
3.1 实验设置
3.1.1 实验数据集
本文使用了3个公开的数据来验证本文方法的有效性:
1)MovieLens 是一个被广泛使用于验证CF 算法有效性的电影评分数据集。MovieLens 有多个版本,在本文的实验中选择含有约100 万条交互记录的版本ML-1M。因为在这个版本的MovieLens数据集中,每个用户都至少含有20条交互记录。
2)Foursquare数据集。该数据集相当稀疏,为了能更好地评估本文的模型,先对Foursquare 进行过滤,使得这个数据集中每个用户至少含有30条交互记录。
3)ratings_Digital_Music 数据集(下面简称Music数据集)。该数据集同样极其稀疏,因此对该数据集也进行了同样的过滤,确保每个用户至少含有30条交互记录。
3个数据的具体数值指标如表1所示。
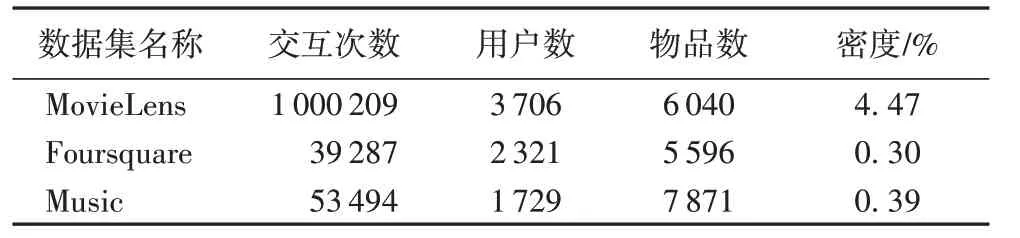
表1 实验数据集的统计信息Tab.1 Statistics of experimental datasets
3.1.2 评估指标与对比算法
为了验证本文将两个模型结合后的评分预测效果的有效性,选择了4个基准方法进行对比实验,分别为ItemKNN(Itembased K-Nearest Neighbors)[16]、DeepICF(Deep Item-based Collaborative Filtering)[17]、MLP 和FISM。其中,ItemKNN 是传统的基于物品的协同过滤方法,DeepICF是解决物品间高阶连接(Higher-Order)关系问题的一种基于物品的协同过滤方法。
在实验中,首先根据数据中的时间戳信息来对每个用户以及物品进行由远及近进行编号和排序。对于3 个数据集,本文都用同样的方法,对每个用户选择最后一次交互的数据作为测试集,其他部分作为训练集。关于评价指标,采用了两种 不 同 的 评 估 方 法:NDCG(Normalized DCG)和HR(Hit Ratio),对于两个评级指标的计算参考文献[15-16]。NDCG和HR的值越大,表示模型预测分值越精确。
3.1.3 参数设置
为了避免模型过拟合,对于每一个方法本文都会在[10-7,10-6,…,10-1,100]范围内来调整正则化项系数的值。对于用户(物品)潜在因子向量的维度embedding_size,本文在进行不同方法对比中选取 32 进行测试,即embedding_size=32;另外也对不同向量维度进行对比,即embedding_size=8,16,32,64。对于学习率,在实验中对不同大小的学习率选择[10-5,10-4,…,10-2]进行实验,选出最佳学习率;本文选择的优化器为标准梯度下降法(Gradient Descent,GD)。
3.2 实验结果与分析
1)UICF模型与3个基准模型在2个评估指标上的效果的展示。
UICF 与基准方法的对比结果如表2 所示,加粗的数值表示最好结果。为了公平地进行比较,表中每个方法的embedding_size 均设为32(本文将在下个实验中比较不同embedding_size 对UICF 的影响)。从表2 中可以看出,融合后的模型UICF 在3 个数据集上的HR 和NDCG 上基本上都取得了最大值(HR 和NDCG 的值越大代表训练出来的模型在测试集上的测试分值越接近实际分值),特别是在Foursquare 和Music两个数据集上,效果更加明显。
融合后的模型UICF 的HR 和NDCG 的值在top-5 和top-10上效果很明显,远大于其他三个对比方法的HR 和NDCG 的值;而在MovieLens 数据集上,这两个值有了提高但并不是很明显。
2)预训练与非预训练对实验效果的影响。
表3 展示了在3 个数据集上分别使用预训练和未使用预训练对实验效果的影响。从表3 可以明显观察出,使用预训练后效果都明显好于没有预训练的,这也进一步说明了,预训练对基于DL 模型的收敛和最终表现效果起到了极其重要的作用。
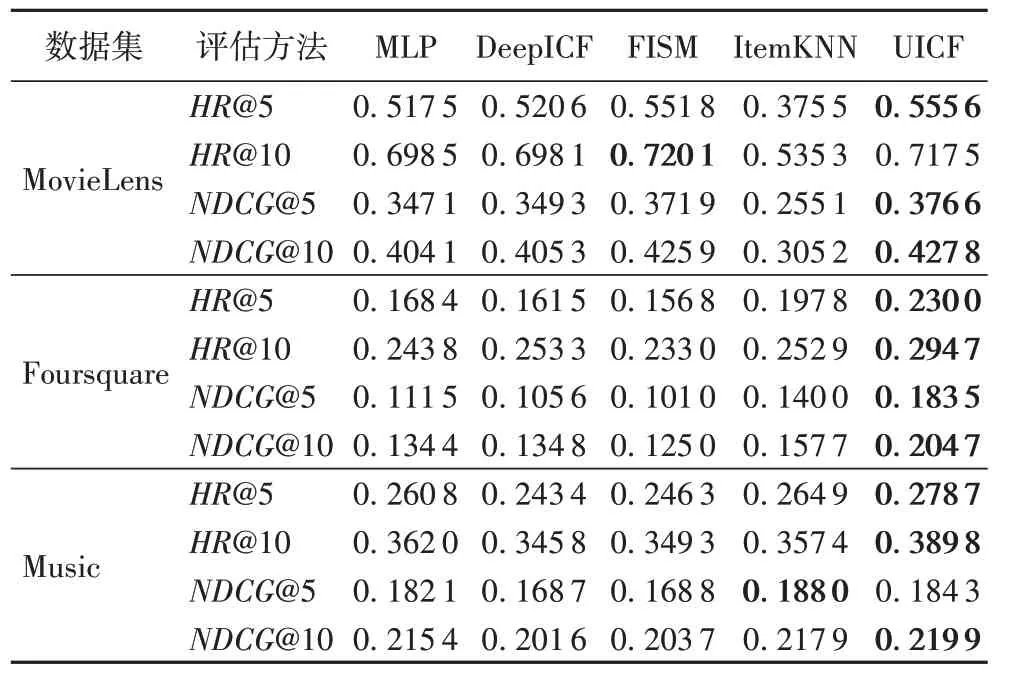
表2 UICF和基准方法的对比结果Tab.2 Comparison between UICF and benchmark methods
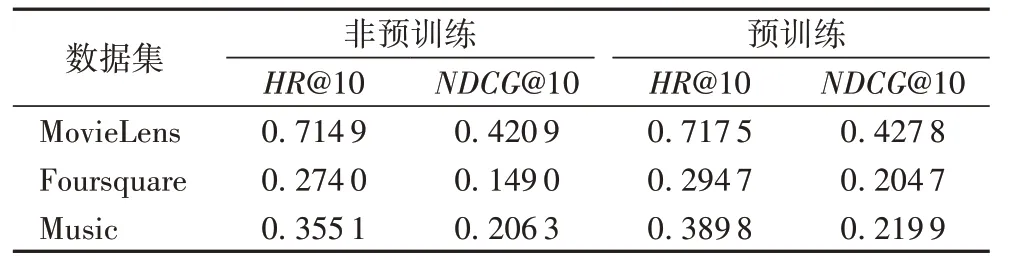
表3 预训练和非预训练方法的对比结果Tab.3 Comparison between method with pre-training and method without pre-training
3)维度d对实验效果的影响。
对于物品维度d 的大小考虑与其他基准方法在3 个数据集上对比NDCG 和HR 值的变化,在实验中不同维度d 对预测评分的影响。表4 为维度d 取值8、16、32、64 时UICF 的不同表现效果。从表4 中可以看出,当维度d 的值分别为8、16、32、64 时HR 和NDCG 的值基本没什么波动,这也说明了维度d的大小对UICF的表现效果影响不大。
4)UICF与基准方法在数据集上的HR@5走势图。
将各方法分别在3 个数据集上运行90 个epoch 后,top@5时HR上的结果如图2所示。可以看出,本文方法把MLP方法和FISM 方法结合后性能得到了提高,经过90 个epoch 的训练,本文的融合方法UICF 在3 个数据集上的结果好于对比方法;而且UICF 模型从开始训练到训练结束时HR 值的变化不大,这是因为FISM 和MLP 这两个模型在结合前都经过预训练,收敛较快。在MovieLens 和Foursquare 数据集上,UICF 模型的HR 从开始上涨到一定值后就保持不变了,UICF 模型的效果高于其他几种对比方法;在Music 数据集上,HR 的值在0.23与0.28之间波动相对很大,这是由于学习率设置较大造成的,但这并不影响它的效果优于其他对比方法。
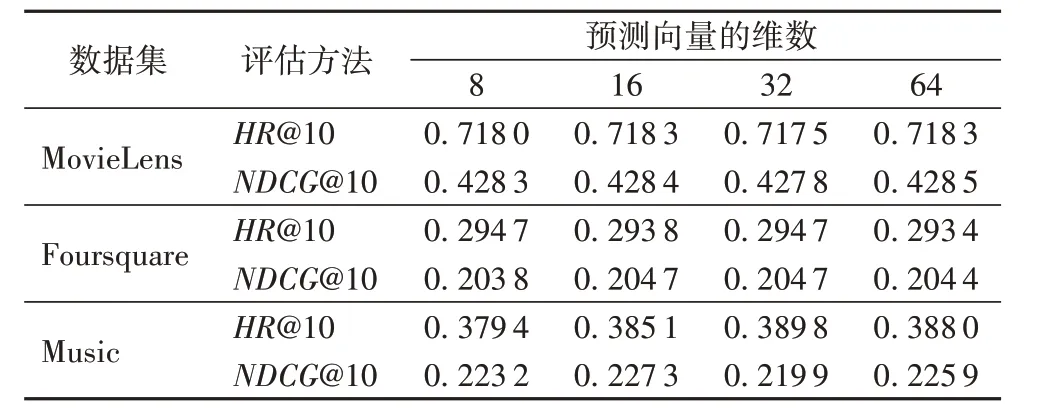
表4 维度大小的影响Tab.4 The impact of dimension size
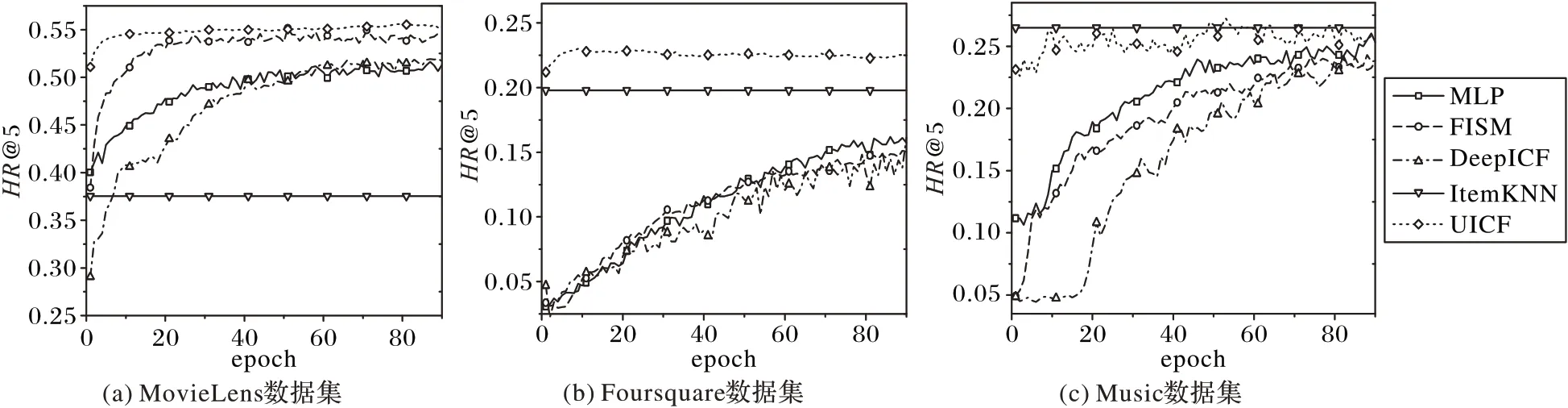
图2 UICF和基准方法在3个数据集上的HR@5走势图Fig.2 HR@5 of UICF and benchmark methods on three datasets
4 结语
本文提出了FISM 模型和MLP 模型结合后的UICF 模型,并通过实验验证了UICF 模型的有效性。本文主要利用了基于物品的推荐方法假设用户倾向于选择与他们之前喜欢的物品相似的物品,因此利用物品的相似作为推荐的依据,在解决数据稀疏性上具有优势。
