耦合火焰不稳定的爆炸超压预测*
2020-04-09李艳超毕明树
李艳超,毕明树,高 伟
(大连理工大学化工学院,辽宁 大连 116024)
为缓解化石类能源引起的环境问题,碳氢类气体燃料(如天然气和液化石油气)正广泛应用于内燃机和涡轮机等供能系统。但在制备、存储、输运及使用碳氢类气体燃料过程中,不可避免地会发生燃料泄漏,进而引发燃烧和爆炸事故。由于火焰不稳定的存在,膨胀火焰表面会出现胞格结构,进而引起火焰加速并导致爆炸超压的增强[1-3]。为降低爆炸灾害后果,建立考虑火焰加速效应的爆炸超压预测模型势在必行。
为此,国内外学者对爆炸超压预测进行了深入的研究。基于三点假设:(1) 爆炸过程中火焰表面始终光滑、(2) 火焰前端未燃气体被绝热压缩、(3) 分压升高正比于已燃气体质量分数,Dahoe 等[4]建立了预测球形容器爆炸超压的光滑火焰模型:
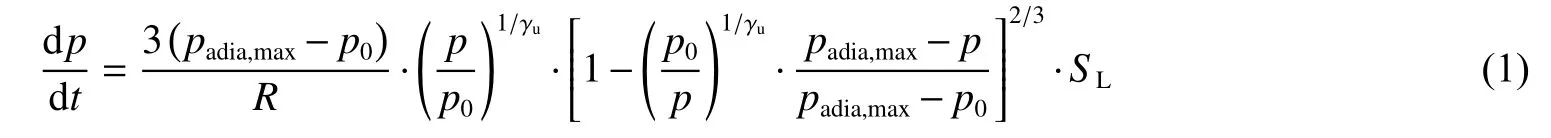
式中:p 为预测爆炸压力,padia,max为绝热最大爆炸压力,p0为初始压力,R 为密闭腔室半径,γb和γu分别为已燃区域和未燃区域的比热比,SL为层流燃烧速度。
假设火焰前端未燃气体被等温压缩,且已燃区域和未燃区域比热比相等(γu=γb=1),Bradley 等[5]对微分方程(1)进行简化:
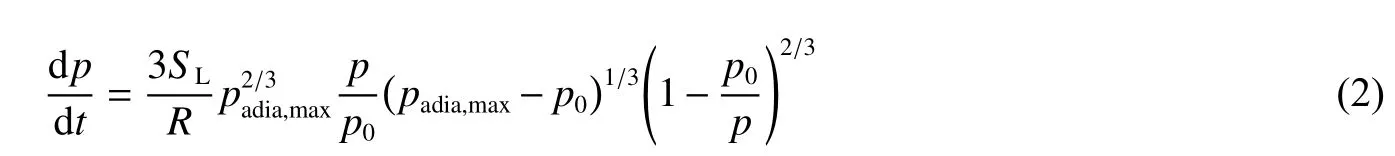
Lautkaski[6]对偏微分方程(2)进行简化积分,推导出了受限空间内预测爆炸超压的立方根定律,但该模型仅适用于Δp≤p0的情况,具体的:
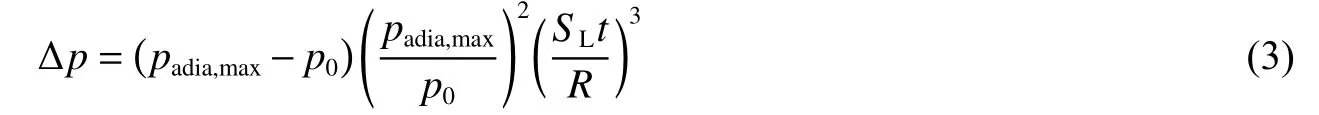
值得注意的是,上述爆炸超压预测模型均假设爆炸过程中膨胀火焰始终光滑。Kuznetsov 等[7]对比了常压阶段和升压阶段的富燃氢气/空气火焰形态,发现常压阶段火焰表面始终光滑,升压阶段形成了胞状火焰。Jiang 等[8]实验分析了爆炸压力升高对胞状火焰结构的影响规律,指出爆炸压力升高初期,平均胞格面积快速减小,随着爆炸压力的继续升高,平均胞格面积趋于定值,且该定值与氢气掺混比无关。基于分形火焰理论,假设火焰完全湍流化,Nishimura 等[3]对方程(1)进行了修正:
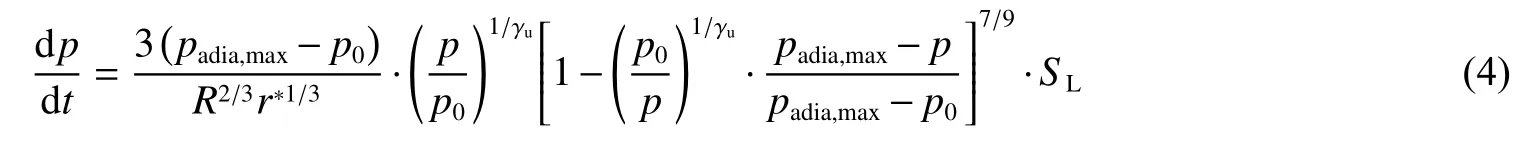
但该模型的预测精度强烈依赖于火焰失稳的临界半径,而且临界半径难以预先确定。
虽然爆炸超压预测模型已有不少,但均未充分考虑火焰加速对爆炸超压的增强效应。基于此,本文揭示了定容燃烧阶段火焰失稳机理,通过引入褶皱因子,修正了光滑火焰模型,建立了耦合火焰不稳定的爆炸超压预测模型。
1 实验装置和实验方法
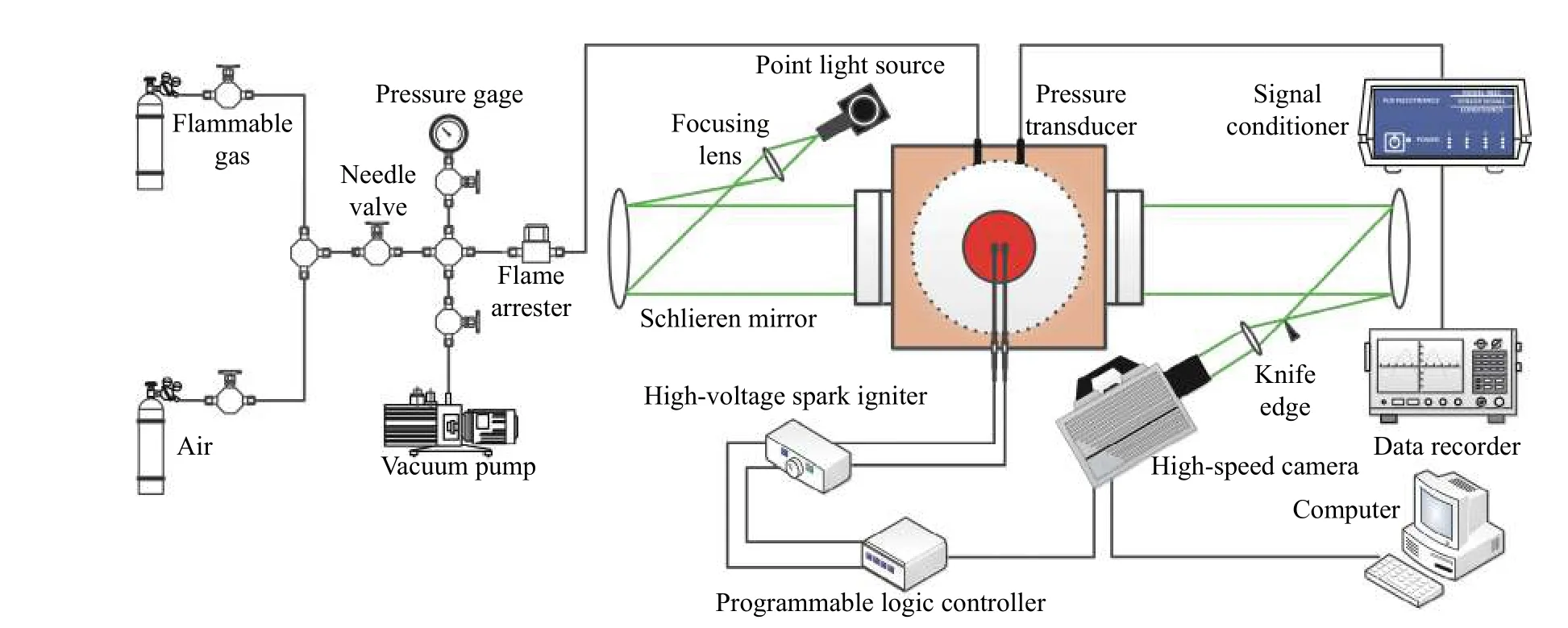
图 1 实验装置图Fig. 1 Experimental apparatus
验装置包括配气系统、高速纹影系统、压力采集系统、高压点火系统和时序控制系统。高速摄像机的拍摄频率为105s−1。采用压电式压力传感器采集球形燃烧室内瞬态爆炸压力,压力数据使用横河数据采集仪记录,记录频率为105s−1。高压点火器、高速摄像机、计算机均由时序控制器进行控制。
2 结果与讨论
2.1 火焰失稳传播和爆炸超压的耦合机制
忽略浮力不稳定,膨胀火焰失稳主要受热扩散不稳定和流体动力学不稳定控制。热扩散不稳定可用刘易斯数表征,流体动力学不稳定可用热膨胀比和火焰厚度表征。其中刘易斯数、热膨胀比和火焰厚度的计算公式如下[11-13]:

式中:Le 为刘易斯数,DT为热扩散系数,DiM为质量扩散系数,σ 为热膨胀比,ρu为未燃气体密度,ρb为已燃产物密度,δ 为火焰厚度,λ 为热传导率,cp为定压比热容,SL为层流燃烧速度,Tad为绝热火焰温度,T0为燃料初始温度。
考虑火焰前端未燃气体被绝热压缩,且假设燃烧反应瞬间达到平衡状态,进而计算整个爆炸过程中的刘易斯数、热膨胀比和火焰厚度。图2 给出了甲烷/空气火焰形态特性和爆炸超压的耦合关系。本研究将爆炸压力低于初始压力10%的燃烧阶段视为定压阶段,爆炸压力高于初始压力10%的燃烧阶段视为定容阶段[14]。定压阶段,火焰表面整体光滑;定容阶段,火焰表面呈现典型的胞格结构。在整个爆炸过程中,刘易斯数变化不大,近似等于1,这意味着热扩散不稳定对火焰失稳或稳定均不起任何作用。热膨胀比和火焰厚度比值在常压阶段几乎不变,但随着爆炸压力的升高,热膨胀比和火焰厚度的比值快速升高。上述结果表明,对于当量比Φ=1.0 的甲烷/空气爆炸,定容燃烧阶段火焰失稳可归因于增强的流体动力学不稳定。
图3 给出了丙烷/空气火焰形态特性和爆炸超压的耦合关系。定压阶段和定容阶段的火焰形态迥异,胞状火焰仅在定容燃烧阶段形成。对于丙烷/空气火焰,尽管刘易斯数在整个爆炸过程中变化不大,但刘易斯数却始终大于1。这意味着热扩散不稳定能够对膨胀火焰起稳定效应。定压阶段,热膨胀比和火焰厚度比值变化不大,但在定容阶段,该比值迅速升高,这意味着流体动力学不稳定对火焰失稳效应逐渐增强。结合刘易斯的变化趋势可知,定容燃烧阶段,热扩散不稳定和流体动力学不稳定相互竞争,并最终导致火焰失稳。

图 2 甲烷/空气火焰形态特性和爆炸超压的耦合关系(Φ=1.0)Fig. 2 Couplings of flame morphology and explosion pressure of stoichiometric methane/air mixture (Φ=1.0)

图 3 丙烷/空气火焰形态特性和爆炸超压的耦合关系(Φ=1.0)Fig. 3 Couplings of flame morphology and explosion pressure of stoichiometric propane/air mixture (Φ=1.0)
2.2 耦合火焰不稳定的爆炸超压预测模型
基于2.1 节可知,在增强的流体动力学不稳定作用下,胞状火焰会出现在定容燃烧阶段,这必然会增加火焰燃烧表面积,进而增强爆炸超压。因此,爆炸超压预测必须考虑定压阶段和定容阶段的火焰形态差异。通过引入褶皱因子ΞΔ,褶皱火焰模型建立如下:

式中:γ 为未燃气体绝热系数,ΞΔ为褶皱因子。
在增强的流体动力学不稳定作用下,胞状火焰呈分形特性,基于文献[15],采用等效面积和等效周长方法,可知爆炸过程中分形火焰的褶皱因子极限值是ΞΔmax=2.464 9。对于光滑火焰模型,褶皱因子始终等于1.0;对于湍流火焰模型,褶皱因子始终等于2.464 9;对于褶皱火焰模型,假设褶皱因子以指数形式从ΞΔ=1.0 增长,且极限值是2.464 9,详细如下:

另外,本研究对比了绝热压缩和等温压缩对爆炸超压预测的影响规律。绝热压缩条件下,层流燃烧速度的计算公式如下[16-17]:

等温压缩条件下,整个爆炸过程中层流燃烧速度始终等于初始条件下层流燃烧速度,即Φ=1.0,对于甲烷/空气混合气体,SL=0.36 m/s;对于丙烷/空气混合气体,SL=0.345 m/s。
2.3 尺度效应对爆炸超压预测的影响规律
图4 给出了当量比Φ=1.0 的丙烷/空气爆炸超压预测。可以发现,光滑火焰模型忽略了火焰不稳定对燃烧速率的增强作用,因此光滑火焰模型预测的爆炸压力远低于实验压力。对于光滑火焰模型,等温压缩预测的爆炸压力明显低于绝热压缩预测的爆炸压力,原因在于绝热压缩可增加层流燃烧速度。点火后,假设膨胀火焰完全湍流化,火焰褶皱程度被显著高估,进而造成理论预测压力偏高。充分考虑爆炸过程中火焰形态由光滑向胞状结构的转捩过程,假设褶皱因子以指数形式增加,褶皱火焰模型预测的爆炸压力和实验压力基本吻合。
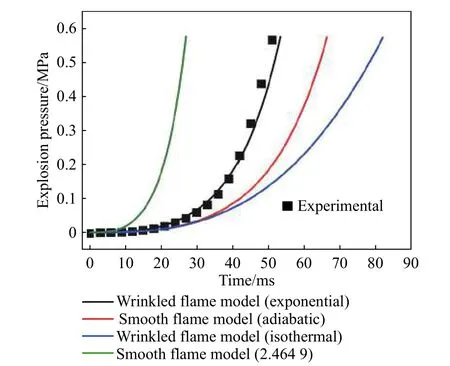
图 4 丙烷/空气爆炸超压预测(14 L 燃烧腔室)Fig. 4 Explosion pressure prediction of stoichiometric propane/air mixture in a 14 L chamber
图5 给出了当量比Φ=1.0 的甲烷/空气爆炸超压预测的尺度效应。燃烧腔室体积V=0.12 m3,V=1.25 m3、V=25.6 m3的压力数据摘自文献[18-20]。随着密闭腔室尺度的增加,湍流火焰模型均高估了爆炸超压,光滑火焰模型均低估了爆炸超压。另外,相比于丙烷/空气爆炸,甲烷/空气爆炸的绝热光滑火焰模型和等温光滑火焰模型的预测值相差不大。当燃烧腔室体积满足0.014 m3≤V≤1.25 m3时,实验压力处于褶皱火焰模型和绝热光滑模型计算值之间,这说明V≤1.25 m3时,褶皱火焰模型会高估火焰表面的褶皱程度。当燃烧腔室体积增大至25.6 m3时,流体动力学不稳定随着火焰尺度的增加而增强,火焰褶皱加剧,火焰传播速度加快,因此该腔室尺度下褶皱火焰模型能成功预测爆炸压力。
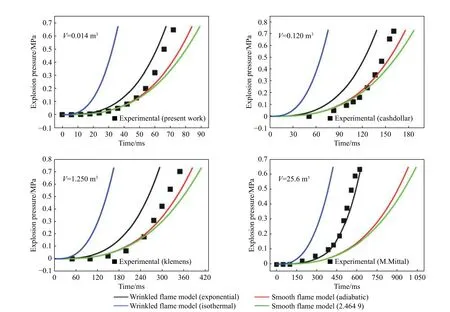
图 5 甲烷/空气爆炸超压预测的尺度效应(Φ=1.0)Fig. 5 Scale effect of explosion pressure prediction of stoichiometric methane/air mixture (Φ=1.0)
3 结 论
为预测密闭腔室内爆炸压力行为特性,本文首先揭示了火焰不稳定和爆炸超压的耦合机制,之后通过向光滑火焰模型引入褶皱因子,建立了考虑火焰不稳定的褶皱火焰模型和湍流火焰模型,最后揭示了尺度效应对爆炸超压预测的影响规律。结论如下:
(1)随着爆炸压力的升高,流体动力学不稳定增强,火焰失稳加剧,且在定容燃烧阶段,胞状火焰形成;
(2)相比于实验压力,光滑火焰模型忽略了火焰不稳定,进而导致理论预测值偏低,且绝热压缩下理论预测压力高于等温压缩下预测值;湍流火焰模型会高估膨胀火焰褶皱程度,理论计算值明显高于实验压力;
(3)通过改变气体种类和密闭腔室体积,褶皱火焰模型在一定程度上可以成功再现甲烷/空气和丙烷/空气的爆炸压力。
