应用改进迭代最近点方法的三维心脏点云配准

王 宾，刘 林，侯榆青，贺小伟

(西北大学 信息科学与技术学院，西安市影像组学与智能感知重点实验室 , 陕西 西安 710127)

1 引 言

三维点云配准技术就是求解不同点云之间的旋转平移变换，将源点云调整到和目标点云相同的坐标位置，实现点云表达的实物信息的融合,在三维轮廓测量[1],医疗诊断和图像处理[2]，虚拟现实[3]和逆向工程[4]等领域有着重要作用。

在目前流行的医学图像分割方法中，大多数研究者将图谱配准或者关键特征点配准与机器学习的方法结合起来，首先通过图谱配准或关键点配准得到图像分割的初始位置或者统计概率图，然后通过各种机器学习的方法对分割结果进一步精确微调。大多数情况下单个图谱因不能体现个体间的差异而难以取得满意的结果，所以许多研究者通过整合多个图谱单独配准的结果来弥补这些差异。在基于多图谱配准的医学图像分割方法中[5-6]，由于生物体自身的差异以及器官的形变、蠕动等原因，导致不同样本中组织器官的形状、位置等有一些偏差，为了确立各图谱与目标图像之间的对应点关系，需要选择目标图像作为参考来配准所有图谱。由于心脏是所有器官中形状最为复杂的，因此三维点云数据模型复杂，不同图谱和目标图像之间具有一定差异；同时，在进行CT心脏数据分割时，由于轮廓不清晰以及人为分割误差等因素可能造成数据部分残缺，这几种情况均加大了配准的难度。

为了提高三维心脏点云数据配准的精度和速度，本文采用先粗配再细配的配准方法。目前常用的粗配准方法主要包括重心重合法[7],标签法[8]和特征提取法[9]。重心重合法通过计算两个模型的重心坐标将其重心重合，这种方法的优点是可以缩小平移差异，缺点是无法缩小旋转差异；标签法通过检测时人为贴上的特征点进行定位，从而将两个模型的位置大致调整到同一个坐标系下，这种方法的缺点是过于依赖新加入的特征点，人为因素对于结果的影响比较大；特征提取法一般根据提取到的平面特征、轮廓特征和边角特征等将两个模型表面特征相同部分重合使其初始位置差异进行缩小，这种方法的缺点是要求模型具有足够多的明显特征。迭代最近点算法(Iterative Closet Point, ICP)是Besl和Mckay[10]在1992年提出的一种精确配准算法。由于其思想简单，容易理解，方便操作和良好的配准效果而成为了主流的配准算法，在各种领域的配准问题上得到了广泛地应用[11-12]。但是，传统的ICP算法对于初始值的敏感性比较高，并且在每次迭代中都对点云数据进行全局搜索以查找对应点，所以计算量大，而且，对于较为复杂的两个模型不能得到良好的配准结果。针对传统ICP算法的缺点，中外许多学者提出了各种改进算法以提高算法的速度和精度。Rusinkiewicz等[13]提出基于法线空间的均匀采样方法，在具有较少特征点的点云进行配准时，该方法可以提高配准速度。Chen等[14]采用待配准点云的点法线与参考点点云的交点确定对应点，该方法能减少迭代次数并加快算法收敛速度，但在某些情况下鲁棒性较差。王欣等[15]提出基于点云边界特征点的改进ICP算法，提高了逆向工程中点云数据配准的效率和精度。Chetverikov等[16]提出的TrICP算法基于稳健统计分析中的最小截断二乘法的一致性对点云进行配准，适用于点云初始值比较差的配准，该方法可以提高配准精度，但是仍会有异常数据影响结果准确性，并且该方法在效率上改善不大。

为了解决多图谱配准中心脏点云数据在具有复杂形状和局部残缺情况下的配准问题，考虑到主成分分析法(Principal Component Analysis, PCA)在特征降维和图像去噪的广泛应用[17-18]，本文采用主成分分析法进行粗配准[19-20]，用KD-tree进行最近点搜索提高搜索速度，在精配准方面提出了基于双向距离比例的ICP算法提高配准的精度，最后使用加权最小二乘法迭代求解坐标转换[21]。

2 基本原理

2.1 模型的粗配准

在精确配准之前，由于两个模型的点集处在同一坐标系的不同位置，没有足够多的重复率，初始位置差异较大，因此点集迭代初始值不能满足精确配准的要求。在点云数目较大的情况下，进行最近点搜索时，算法的复杂度和计算量会剧增，为了提高算法执行效率和配准精度，在进行精确配准之前，先对两个点集进行全局的粗配准，以便为精确配准提供良好的初始值。

综合考虑各粗配准方法的优缺点，本文使用的粗配准方法是主成分分析法(PCA)，算法实现步骤为：

(1)设n维的三维点数据集P={P1,P2,P3,...,Pn}，计算其均值和协方差矩阵cov；

(2)对矩阵cov进行特征向量分解，得到的正交特征向量作为点集P的三坐标轴x,y,z，以其均值作为坐标系原点O；

(3)按照上述方法分别对两组点云数据集计算坐标系，并求取两组点云数据集的参考坐标系间的刚体转换参数，以实现点云数据集间的粗配准。

2.2 模型的精配准

精确配准即局部配准，在粗配准的基础上，如何精确求解两点云数据集之间刚体转换参数是整个配准过程中最为重要和核心的部分。本文提出基于双向距离比例的ICP算法提高配准的精度，利用迭代算法求解基于加权最小二乘理论的最优解，得到具有较高精度的全局最优化刚体转换参数，完成两个点云数据集的配准。针对点云配准的本质问题，即求解两个点集之间的旋转矩阵和平移矢量，本文采用奇异值分解法(Singular Value Decomposition, SVD)进行求解。

2.2.1 传统的ICP算法

假设源数据点集P：{Pi,i=1,2,...,Np}及目标数据点集Q：{Qi,i=1,2,...,NQ}，每一次迭代中，执行如下步骤：

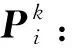
(1)

(2)通过最小二乘法计算最优刚性变换：

(2)

(3)对Pk+1做旋转平移变换：

(3)

(4)计算平均距离dk+1：

(4)

当平均距离dk+1小于一定的阈值τ时，迭代终止，否则重复迭代直到dk+1<τ或迭代次数达到预设的阈值为止。

2.2.2 改进的ICP算法

针对目前常用的ICP算法存在的问题本文提出了基于双向距离比例改进的ICP算法，使其更加方便的应用在基于多图谱配准的医学图像分割问题上，同时保证配准精度和速度。

在经典的ICP算法中，计算过程中的每一组匹配点对具有相同的权重，对于错误匹配点没有进行任何处理，这样会使得一些错误匹配点对影响配准结果的精确度。目前常用的TrICP方法是基于最小截断二乘法的思想，即将所有匹配的点对之间的距离计算并排序，把残差较大的直接去除，该方法可以减小离群点对配准结果的影响，但是去除匹配点对的比重不好掌握，如果去除过多，有可能去掉正确匹配点对，如果去除较少，有可能仍旧会残留错误匹配点对，匹配精度无法保证。因此，受加权最小二乘法思想的启发，给每组匹配点对一个权值，本文提出基于双向距离比例的ICP算法来提高配准的精度，既能减少误匹配对配准精度的影响，也能保证搜索到更多的点对参与最终配准结果的求解。算法的主要思想是:对于目标数据中的点Qi在源数据点集中寻找最近的点Pi，如图1(a)所示，然后对点Pi反向在目标数据中寻找最近的点Ql，搜索到的点Ql有可能是点Qi本身，也有可能是其相邻点，如图1(b)所示。

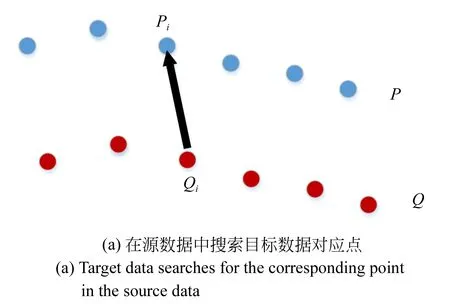
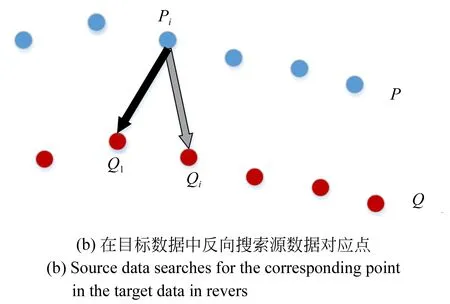
图1 双向距离搜索示意图

分别建立双向匹配，如式(5)和式(6)所示：

(5)

(6)

其中，Rk-1，tk-1分别为每次迭代过程中的旋转矩阵和平移矢量。

采用式(7)基于双向距离求比值。

(7)

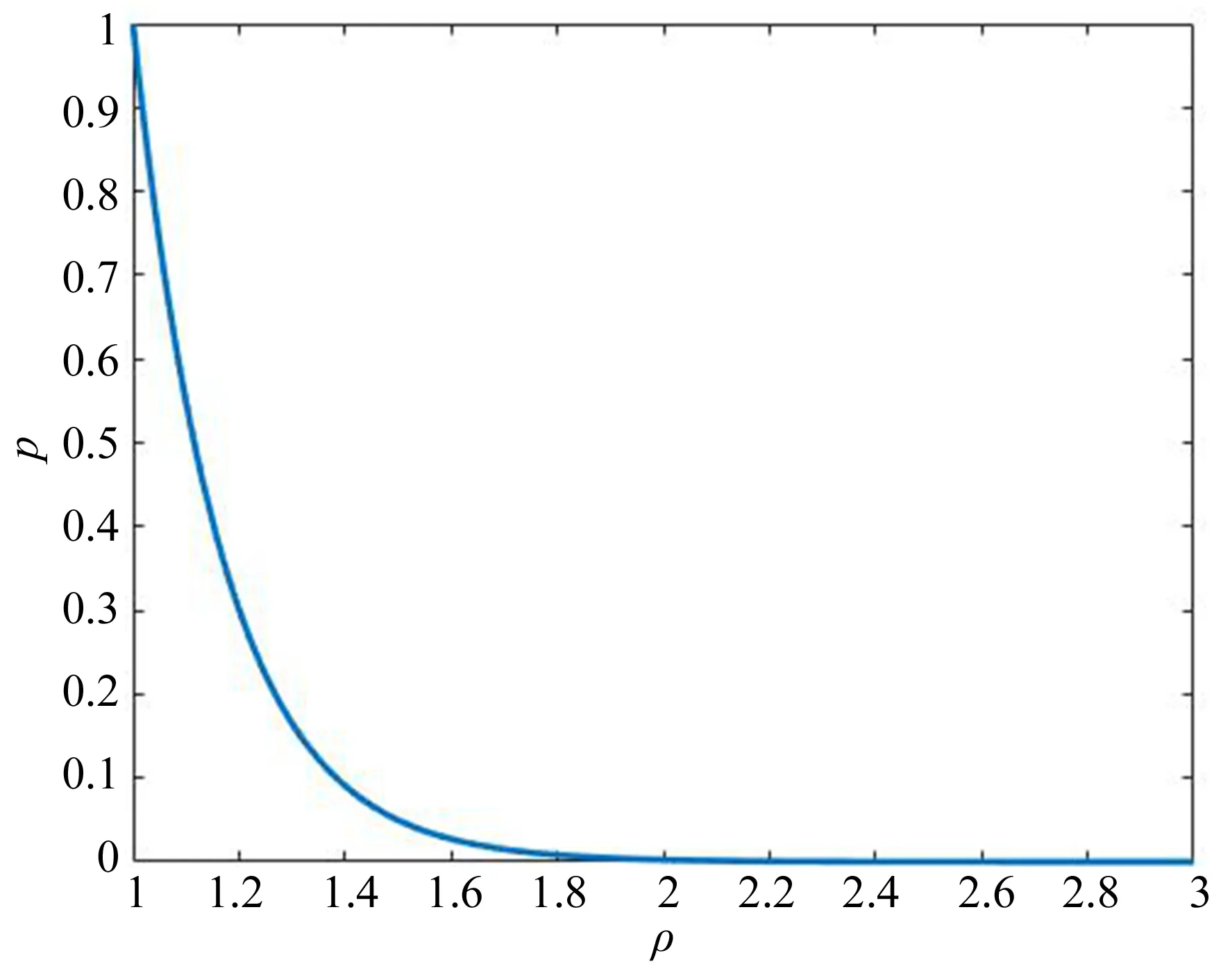
图2 本文所用指数函数特性示意图Fig.2 Exponential function characteristic diagram used in this paper

在此算法中，基于加权最小二乘求解最优变换，权重的赋值即概率值是需要解决的重要问题。根据指数函数的特性，引入一个指数函数来计算概率值pi，有效反映每一点对双向距离比值与应该赋予权重之间的关系，本文所采用指数函数特性如图2所示。其中，pi是与ρi相关的一个概率值，此概率值可以反应点对是否属于内点的概率，即正确匹配的概率。

概率值的计算如式(8)所示：

pi,k=e-λ(ρi,k-1),

(8)

其中：λ是预设参数，依据指数函数的特性,可以反映出随着双向距离的比值ρi增大，概率值pi下降的特性。如果双向距离相等，那么最大概率的被视为内点，如果ρi比值增加，概率值会下降。

本文以pi值作为权重，用一个新的函数表示加权最小二乘法：

(9)

通过加权最小二乘计算最优变换：

(10)

使用SVD算法求解对应点集，具体步骤如下：

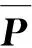
Step2 以重心为三维坐标系的原点重建源数据点集和目标数据点集坐标系，并以Pi′和Qi′作为下一步的运算数据，以简化运算。

(11)

Step3 以Pi′和Qi′为基础构造矩阵H，利用奇异值分解法分解矩阵H，得到矩阵U和V。

(12)

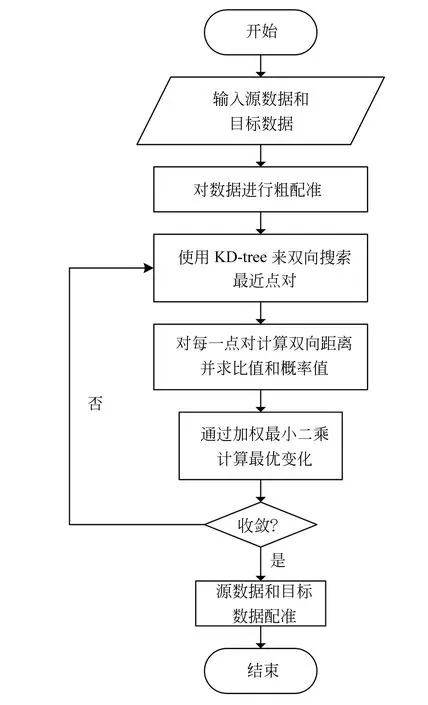
图3 改进的ICP算法流程图Fig.3 Flow chart of improved ICP algorithm

Step4 由U和V，计算旋转矩阵R和平移矢量t。

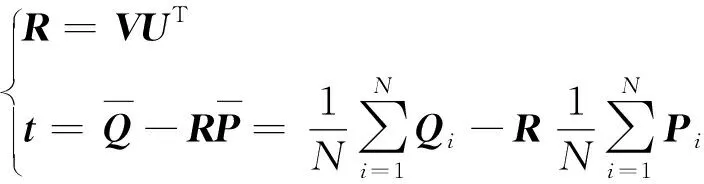
(13)

改进的ICP算法总体描述为：首先输入源数据和目标数据，对其进行粗配准；然后使用KD-tree进行双向距离搜索，并且对每一点对计算双向距离比值和概率值；最后利用加权最小二乘计算最优变换，运用奇异值分解法得到最终的变换矩阵。判断是否收敛，如果不收敛，重复迭代，如果收敛，源数据和目标数据配准并输出最终结果，算法流程图如图3所示。

3 实验与结果分析

在CT心脏点云数据的配准中，主要面临具有较大初始位置差异、较大形状差异和局部残缺的心脏点云数据配准的精度以及速度问题，因此，本文设计两组实验验证本文算法在不同情况下的点云数据配准精度以及速度。一组是斯坦福点云数据配准实验，一组是心脏点云数据配准实验。实验中，设置式(8)中的λ=6，最大迭代次数设为150。本部分实验均在配置为3.00 GHz Intel Core i5 CPU 和8.00 GB RAM的个人计算机上完成，计算工具为MATLAB R2015b。

3.1 斯坦福点云数据配准实验

为了验证本文算法对初始值敏感性和初始姿态重叠度具有较好鲁棒性，首先采用公用的斯坦福点云数据设置一组实验，源数据为斯坦福bunny点云数据，目标数据为源数据在三维空间做(Re,te)的较大幅度旋转平移变换，并分别在整个点云数据上随机剔除5%，10%，15%，20%的点云。实验引入参数间相对的误差来衡量配准精度，εR=‖Rk-Re‖F，εt=‖tk-te‖2。其中(Rk,tk)是最终求解的最优变换，(Re,te)是人为对目标数据做的旋转平移变换，‖·‖F是F范数。为了研究本文方法在配准精度和配准速度方面的性能，将本文算法与经典ICP算法和文献18提出的TrICP算法进行了对比。其中，剔除20%比例点云的配准结果如图4所示。

图4 斯坦福bunny数据配准结果Fig.4 Stanford bunny data registration results

通过表1和图5的数据分析可以得出在剔除不同比例点云数目的情况下，TrICP算法通过剔除异常点，较经典ICP算法减小了配准误差，但精度仍不及本文算法，本文算法的相对旋转误差较经典ICP算法减少了48%～49%，较TrICP算法减少了30%～32%，相对平移误差较经典ICP算法减少了47%～52%，较TrICP算法减少了36%～45%。同时，TrICP算法的效率稍优于经典ICP算法，而本文算法采用KD-tree进行双向距离搜索，同时由于配准精度的提高，算法收敛速度快，因此效率大幅优于以上两种算法，并且以上两种算法在残缺程度(剔除点云比例)较大的情况下，相对误差会增大，本文算法在残缺程度较大的情况下依旧可以得到精确的配准结果，同时在减少点云数目的情况下旋转误差和平移误差基本不受影响，趋于稳定，而且由于需要搜索点云数目的减少，配准时间减少，4 500～6 000的点云数目根据模型残缺程度以及模型复杂程度的不同一般只需要0.6～1.3 s的配准时间。因此使用本文方法可以通过减少目标数据点云数目来提高搜索效率，降低时间。通过对斯坦福点云数据配准结果的分析可以初步确定本文改进的ICP算法可以精确高效稳定的解决心脏点云数据的配准问题。

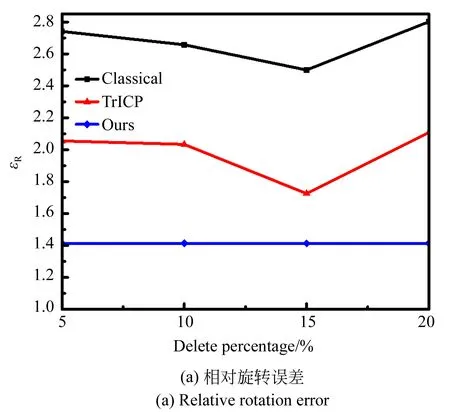
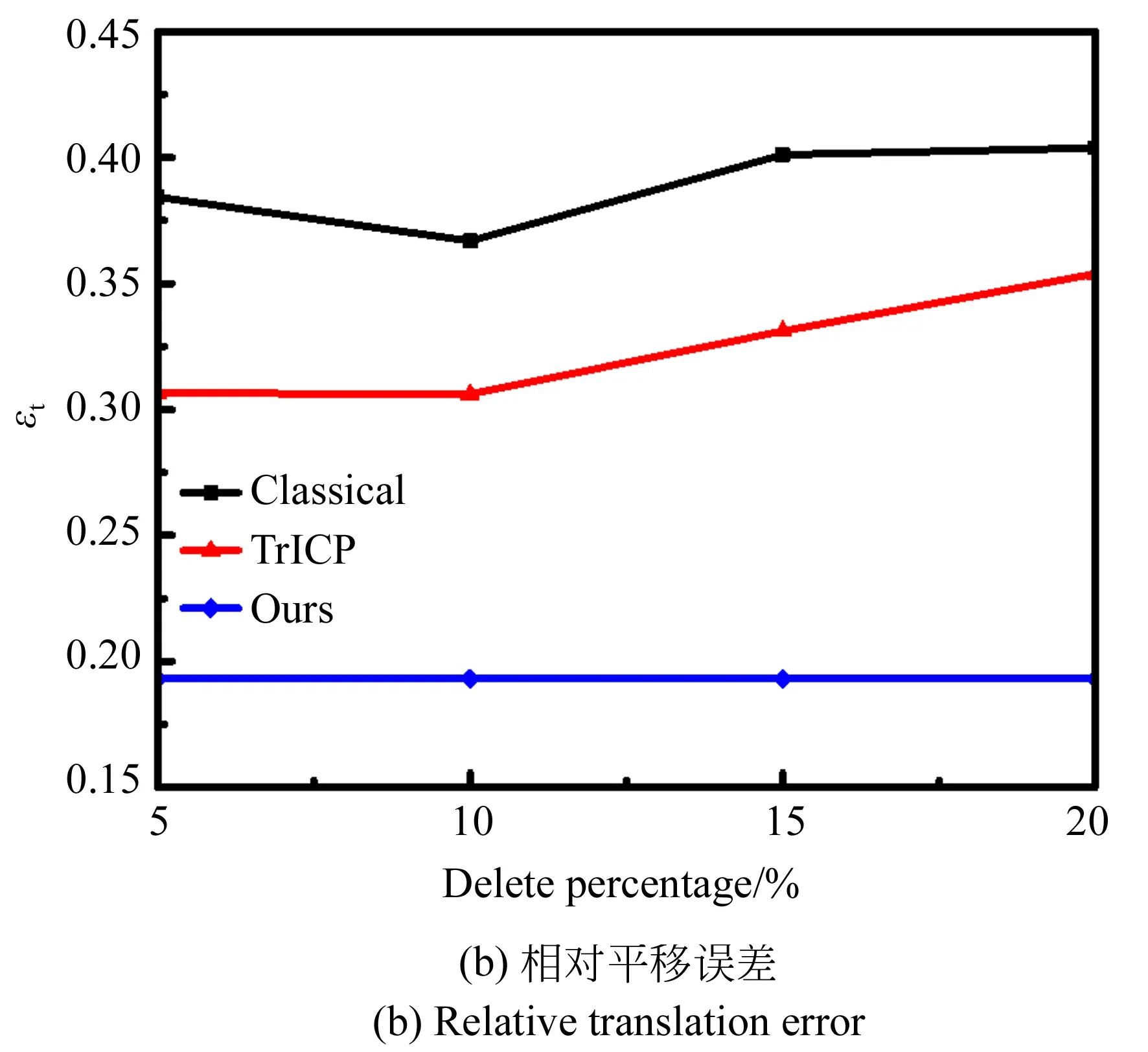
图5 bunny数据配准结果分析Fig.5 Bunny data registration result analysis

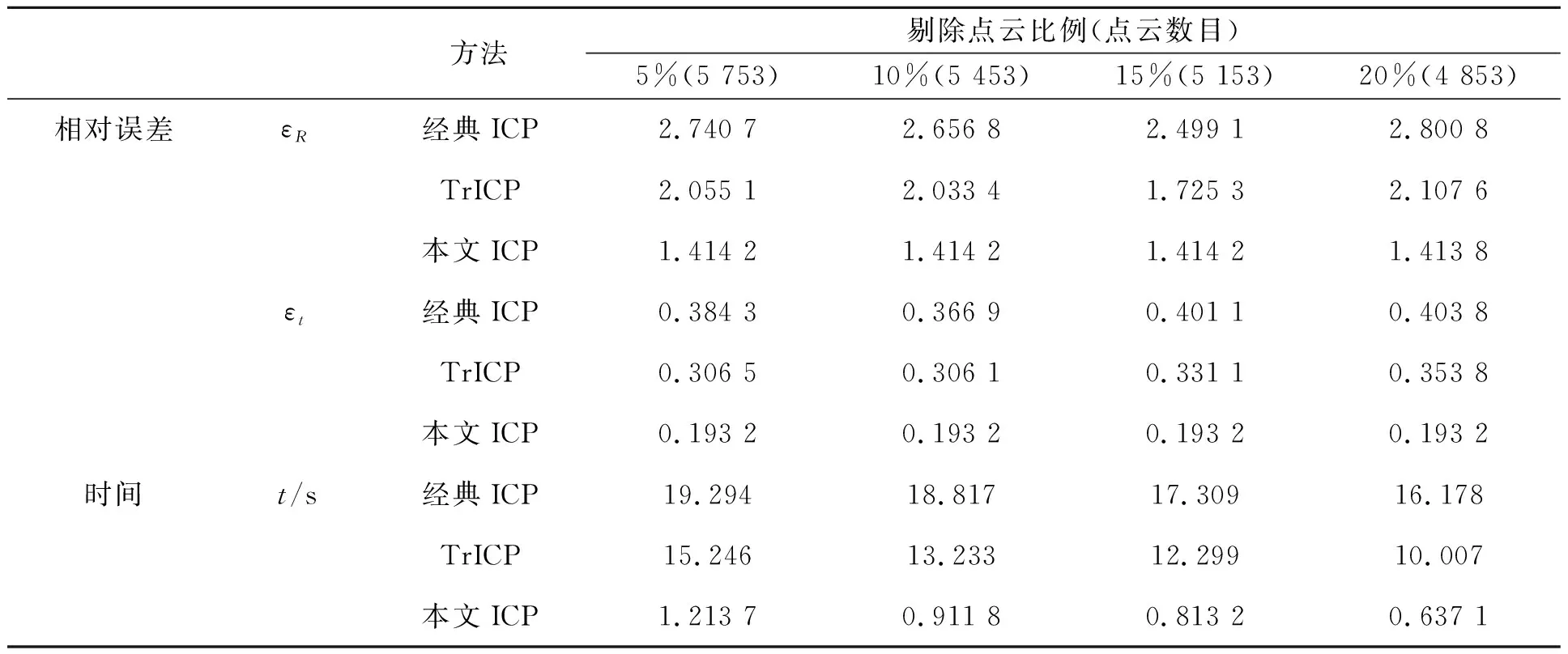
表1 bunny数据配准的定量分析结果

3.2 心脏点云数据配准实验

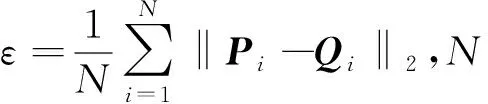
通过观察图6的配准结果可以发现在具有较大形状差异和残缺差异的心脏点云数据配准中，本文改进的ICP算法的配准结果吻合度更高，特别是图谱的边缘部分以及局部形状差异大的部分。通过表2和图7的配准定量分析结果和对比结果也可得到虽然由于模型差异较大导致配准误差较大，但是本文算法的配准精度仍旧高于经典ICP算法和TrICP算法，配准平均误差较经典ICP算法减少了约21%，较TrICP算法减少了约13%。通过对比第一组和第二组的误差可以得到本文方法在第二组心脏配准的误差改善更大，通过观察待配准图谱可以发现，第二个待配准图谱较目标图像之间的残缺更大，特别是心脏上部较目标图像有着明显的形状差异和残缺差异，而第一个待配准图谱较目标图像之间差异较小，由此可以体现出本文方法在具有较大残缺差异和形状

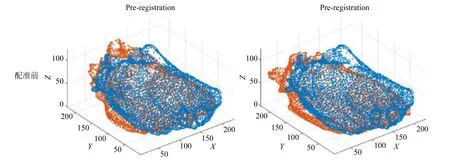
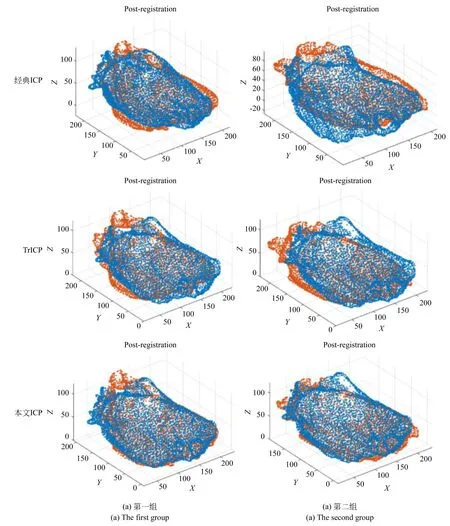
图6 两个图谱与目标图像之间的配准结果Fig.6 Registration result between two maps and the target image

差异时对于精度的提高较经典ICP和TrICP的优势更加明显。在配准速度方面，TrICP算法稍优于经典ICP算法，但仍不及本文算法的配准速度，本文算法由于采用KD-tree进行双向距离搜索，同时由于配准精度的提高，算法收敛速度快，4 500左右的点云数目根据模型复杂程度以及残缺程度只需要1.6～1.8 s左右的配准时间，因此速度大幅优于以上两种算法。

因此，本文改进的ICP算法可以满足基于多图谱配准的CT心脏分割中具有较大初始位置差异、较大形状差异和局部残缺的心脏点云数据之间精确高效地配准。

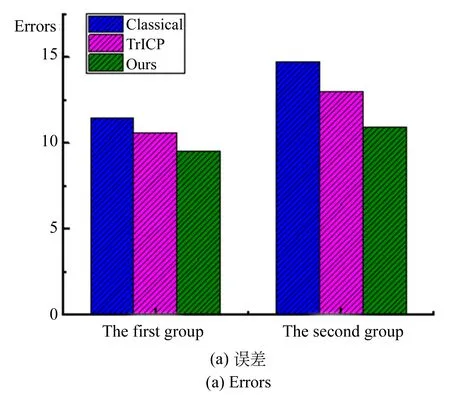
图7 心脏数据配准结果分析

Fig.7 Analysis of cardiac data registration results

表2 心脏数据配准的定量分析结果

Tab.2 Quantitative analysis of cardiac data registration

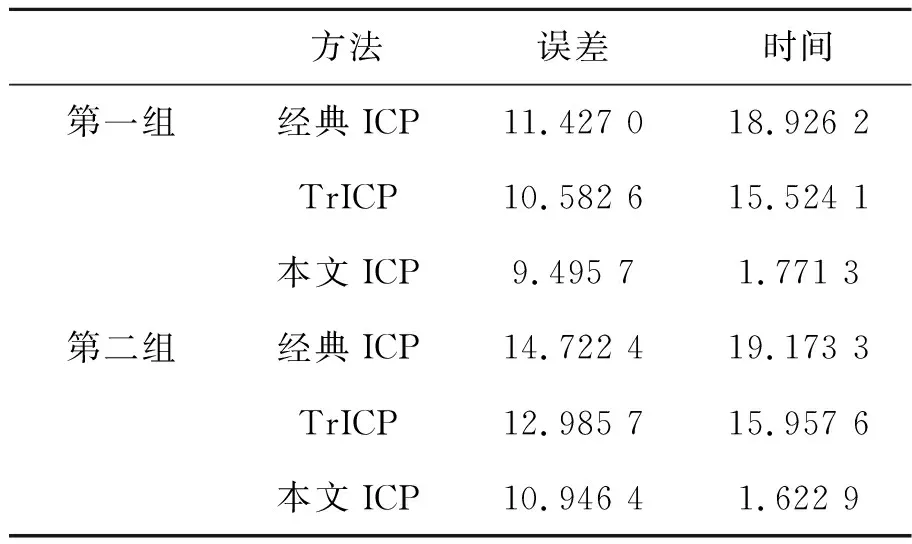
方法误差时间第一组经典ICP11.427 018.926 2TrICP10.582 615.524 1本文ICP9.495 71.771 3第二组经典ICP14.722 419.173 3TrICP12.985 715.957 6本文ICP10.946 41.622 9

4 结 论

为了提高具有较大初始位置差异、较大形状和局部残缺差异的心脏点云数据配准的精度以及速度问题，本文采用一种先粗配再精配的配准方法。首先采用主成分分析法进行粗配准，然后在精配准方面提出了基于双向距离比例的ICP算法提高配准的精度。实验结果表明，本文方法具有良好的稳定性，较高的精度和效率，配准平均误差较经典ICP算法减少了约21%，较TrICP算法减少了约13%。改进算法的优势主要体现在两方面，一是在模型残缺程度较大的情况下配准精度基本不受影响，但由于点云数目减少，配准时间减少，因此可以通过减少目标数据点云数目来提高搜索效率，降低时间；二是在具有较大残缺差异和形状差异时本文算法具有很强的鲁棒性，在配准精度方面的优势更加明显。因此本文算法可以应用于基于多图谱配准的医学图像分割中。进一步优化配准方法，以及将本文配准方法适用于其它应用环境中，比如生物医学的中的不同模态，不同结构的对象配准问题，是下一步研究的方向。