基于导通角调节的双足式尺蠖电机驱动

赵 勃，史维佳*，王丙泉，亓 雪，谭久彬

(1.哈尔滨工业大学 超精密光电仪器工程研究所，黑龙江 哈尔滨 150080;2.超精密仪器技术及智能化工业和信息化部重点实验室(哈尔滨工业大学)，黑龙江 哈尔滨 150080)

1 引 言

压电尺蠖执行器是利用尺蠖作动机理，基于压电材料的逆压电效应和界面间的摩擦传递作用输出精密运动的新式执行器。压电尺蠖执行器具有小质量下的高能量输出、纳米级的位移分辨力、断电情况下可自锁等特性。压电尺蠖执行器具有良好的性能，且经过特殊工艺制造，由多层压电陶瓷片构成的压电叠堆具有十分优良的性能，因此非常适合应用于超精密定位技术领域中[1-5]。

根据钳位单元和驱动单元的装配位置、工作方式，压电尺蠖执行器可分为爬行式、推进式及爬行-推进式三类。由于爬行式压电尺蠖执行器的驱动压电叠堆和钳位压电叠堆都被装配在动子上，工作中势必影响其运动精度和运动稳定性，同时在动子上设计的多组柔性铰链，也势必降低动子自身刚度，工作中容易产生附加变形。而且钳位机构的钳位力较小，导致执行器承载能力较小。推进式压电尺蠖执行器钳位单元和驱动单元都被装配在定子上,由于定子位置是固定不动的，钳位过程和驱动过程稳定可靠,容易产生较大的钳位力和驱动力。此外，动子内部没有任何机械元件和电器元件，其加工质量容易保证,并能保证驱动器具有很大的运动行程[6-8]。该执行器结构合理、原理科学，驱动器整体性能良好、运行稳定。然而，推进式尺蠖电机传统驱动方法中，其步距和驱动速度相互影响无法单独调节，因此无法同时实现高速高精度驱动[9-12]。本文提出一种基于导通角调节的推进式尺蠖电机驱动方法，该驱动方式下电机实现了高速、高位移分辨率，满足超精密领域的需求。

2 电机结构设计及机电耦合模型建立

2.1 单足定子结构设计

按照椭圆运动轨迹方程中两压电叠堆的输出位移耦合方式，非共振激励下椭圆运动轨迹方程可分为位移耦合型和位移解耦型[13-14]两种。

上述两种模型的相同之处在于都是通过两组压电叠堆实现驱动足空间两个方向的运动。压电叠堆是由多层薄片结构堆积形成，每层薄片具有固定的极化方向，施加在每层陶瓷片上反向电场强度不能太大，以防退极化。因此，压电叠堆的驱动电压信号带有正偏置的特征。同时，这种层积结构只能承受轴向正压力，而不能承受拉应力或者是横向的剪切应力。

图1 尺蠖电机单足定子结构Fig.1 Single-foot stator of inchworm motor

根据实际性能要求确定压电叠堆性能，压电叠堆最终采用哈尔滨芯明天科技有限公司的产品XMT150/17×7/18，截面积为7 mm×7 mm的方形，长为18 mm。

图1为V形双足式尺蠖电机单足定子的结构图，该定子由2组压电叠堆、定子金属头、陶瓷球、预紧螺杆、预紧螺母和基体组成。其中，定子金属头将压电叠堆的位移变化传递到驱动足，起到放大微小位移的作用；陶瓷球是定子与动子之间的接触体，作为驱动足驱动动子运动；基体用于支撑压电叠堆，起到机械固定作用；预紧螺杆和预紧螺母与定子金属头、基体配合使用，对压电叠堆进行机械压紧固定。

预紧螺杆一端经螺纹连接旋入定子金属头，另一端穿过基体上的光孔。两组压电叠堆分别压设在定子金属头和基体之间，所有零件经预紧螺母旋紧成一体。在基体后座上留有两个螺纹孔，用于安装、固定定子。

2.2 压电叠堆数学模型

压电材料的本构方程反映了弹性变量(应力T、应变S)和电学变量(电场E、电位移D)间的关系。在忽略非线性因素影响的前提下，压电叠堆应力(应变)-电场(电荷)符合线性关系，在压电叠堆所用方向上有:

S33=s33T33+d33E3，

(1)

D3=d33T33+e33E3，

(2)

式中：S33为压电叠堆所用方向上的应变；s33为压电叠堆的柔度系数；T33为压电叠堆的内部应力；d33为压电叠堆所用方向的压电常数；D3为压电叠堆的电位移；E3为压电叠堆的外加电场；e33为自由状态下压电叠堆的介电常数。

根据应变与位移关系可知，压电叠堆输出的总位移为:

W=ntS33，

(3)

式中：n为压电叠堆层数。将式(1)代入式(3)得到:

W=nt(s33T33+d33E3).

(4)

若压电叠堆一端固定，另一端处于自由状态，则其内部应力T33=0，有:

W=ntd33E3.

(5)

工作中通常考虑施加在压电叠堆上的电压，施加在单层压电片上的电压为：

E3=U/t，

(6)

式中：U为施加在压电叠堆单层压电片上的电压；t为单层压电片厚度。

将式(6)代入(5)得到:

W=nd33U.

(7)

由式(7)可知，当压电叠堆一端固定，一端自由时，其伸长量与所施加电压呈线性关系。

2.3 定子的驱动模型

根据如图1所示的定子结构，如下假设成立：

(1)由两刚性杆连接代替铰链连接；

(2)两刚性杆与水平面的夹角θ1=θ2=45°。

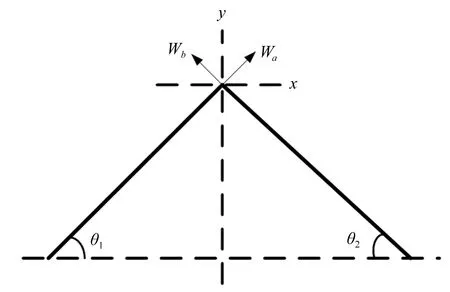
图2 定子位移模型Fig.2 Model of stator displacement

因此，图2为定子位移简化模型，两刚性连杆端点的x位移和y位移分别为：

x=Wacos45°-Wbcos 45°，

(8)

y=Wasin45°+Wbsin 45°.

(9)

连续作动模式下，两组压电叠堆分别被施加两组相位差为π /2的正弦电压，由于压电叠堆不能承受反向电场，这两组电压信号都带有峰峰值一半的正偏置。

定子左右两端的压电叠堆上所施加的正弦电压为：

Ur=Udc(1+sinωt)，

(10)

Ul=Udc(1+cosωt)，

(11)

式中：Ul，Ur分别为左、右两端压电叠堆施加的电压信号；Udc为母线电压。

由压电叠堆输出位移与施加电压的关系式(7)得到输出位移：

(12)

(13)

式中ω为正弦电压的角频率。

由式(12)和式(13)可知，在两刚性连杆两端施加正弦变化的位移时，两刚性连杆端点x，y方向的位移是有一定相位差的正弦信号，消去时间参数。拟合x，y得到两刚性连杆端点的位移轨迹方程为：

(14)

式中M=nd33Udc。由式(14)可知，驱动足的运动轨迹为圆。

为了使定子的驱动效果与驱动效率最大化，仿照尺蠖运动的双足，设计双足定子结构分别与动子紧密接触。一个接触时，另外一个分离，二者实现无缝对接，使驱动稳定且驱动效率最大化，定子与动子接触和分离的临界条件为y=2。

联立式(13)得定子与动子接触和分离的临界时刻为：

(15)

进一步可得两组定子的相位滞后为：

Δφ=(t2-t1)·ω=π.

(16)

在此驱动工作模式下，驱动时间周期T，x和y的位移变化量分别为：

(17)

Δx=2nd33Udc，

(18)

Δy=nd33Udc.

(19)

由式(17)和式(18)可得x方向的速度为：

vx=Δx·2f=4fnd33Udc.

(20)

式中f为驱动电压信号的频率。

由式(18)和式(20)可知，电机的步距、驱动速度均与母线电压Udc成正比，若实现高位移分辨力，驱动速度会因此降低，无法同时实现高速与高位移分辨力。因此，为了解决尺蠖电机高速和高精度难以兼顾的问题，本文提出一种新的驱动方法，在减小步距提高位移分辨力的同时，保证较大的驱动速度。

3 尺蠖电机驱动电路方案设计

3.1 驱动电路方案总体设计

驱动电路系统的重要功能如下：

(1)FPGA模块：通过对50 MHz的基频进行分频，产生所需频率的脉宽调制(Pulse Width Modulation,PWM)信号，作为全桥驱动模块的输入信号;

(2)半桥驱动模块：由于现场可编程门阵列(Field Programmable Gate Array,FPGA)产生的PWM信号无法直接驱动半桥逆变电路，全桥驱动模块将FPGA产生的单极性方波信号转变成双极性方波信号，控制全桥电路的MOSFET管的导通;

(3)半桥逆变模块：对PWM信号进行功率放大，之后通过匹配电路驱动电机;

(4)匹配电路：匹配负载的容性，降低电流尖峰，提高驱动电路效率和可靠性，附带效果可实现滤波。

3.2 双路半桥驱动电路设计

如图4所示，采用FPGA产生S1，S3开关信号，驱动半桥电路中的MOSFT产生驱动电压ua，ub，其周期均为T(角频率ω=2πf=2π/T)，导通角分别为αa，αb，高电平幅值为Udc。

按照傅里叶级数的定义，驱动电压ua，ub可表示为：

ua=Udcαaf+

(21)

ub=Udcαbf+

(22)

由于匹配电路具有低通滤波，通过合理设计截止频率，可只保留直流分量和基波分量，由此可将加在尺蠖电机上的驱动电压ua，ub简化为：

(23)

(24)

令αa=αb=α，由式(8)得到压电叠堆的输出位移为：

(25)

(26)

图3 双路半桥驱动电路Fig.3 Two-way half-bridge drive circuit

图4 开关信号及输出电压波形Fig.4 Switching signals and output voltage waveforms

拟合x，y得到两刚性连杆端点的位移轨迹方程:

(27)

在此驱动模式下，步距、驱动速度的表达式如下:

(28)

(29)

与式(18)和式(20)相比，电机的步距、x方向驱动速度引入了导通角这一新变量，改进的优势如下：

(1)调导通角比调母线电压更容易实现高精度；

(2)母线电压不降低可保证纵向位移不减小，进而保证足够的分离位移，不会出现调速死区；

(3)频率和导通角是两个独立的控制变量，可对步距和驱动速度单独调节，由此可兼顾高位移分辨率与大驱动速度。

4 尺蠖电机运动机理及实验研究

4.1 双足尺蠖电机运动机理

电机的单个定子简化表示为一个刚性的等腰三角形，驱动足位于三角形定点处，压电叠堆位于底边的两个端点处。当左右的两个压电叠堆两端施加相位差为90°的正弦信号时，驱动足以椭圆轨迹振动。

当给定子上的4组压电叠堆分别施加相同幅值、两两相位差为90°的正弦电压时，两个驱动足将以椭圆轨迹进行振动，且振动的相位相差180°。双驱动足的工作模式如图5所示。

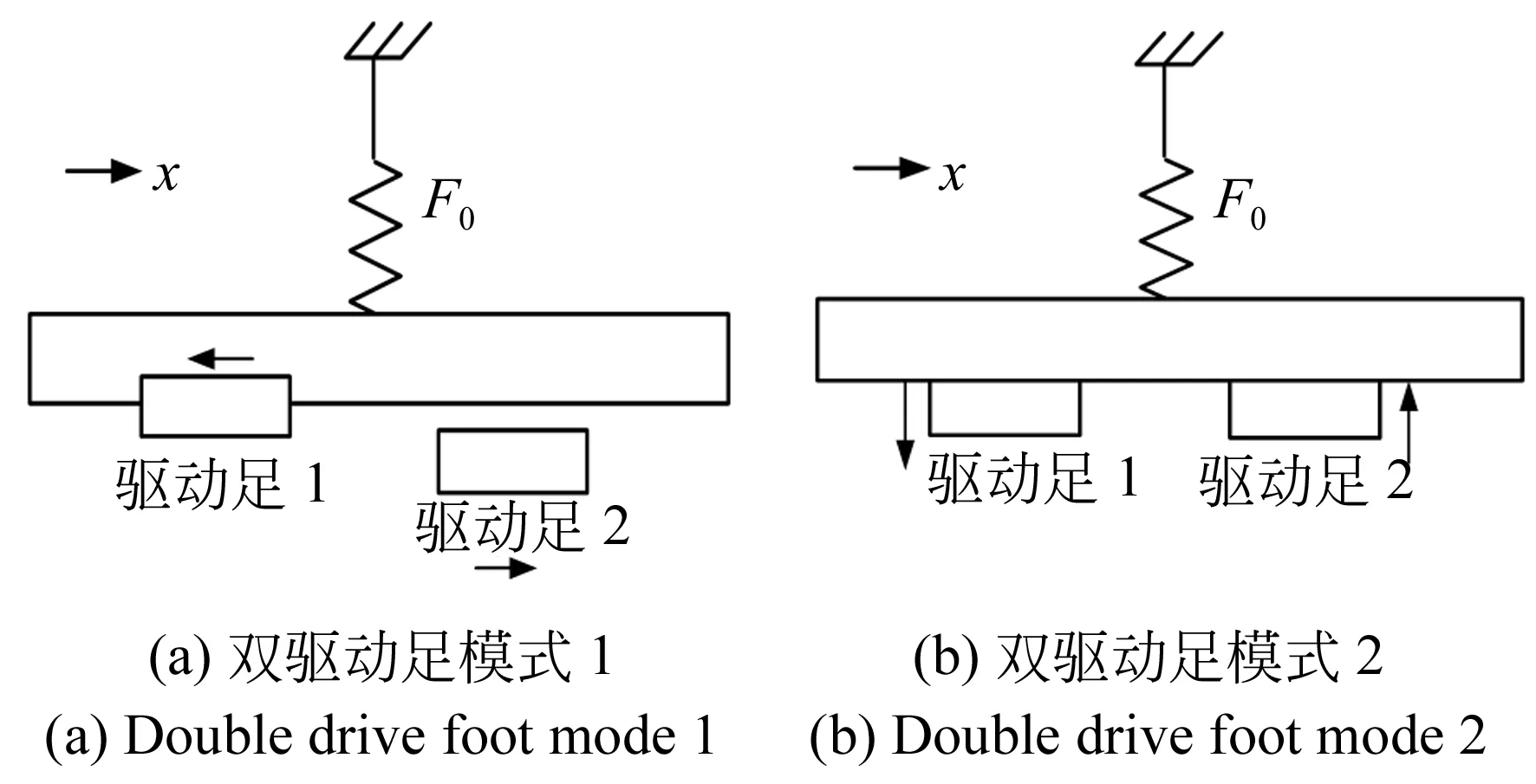
图5 双驱动足的工作模式Fig.5 Working modes of double drive foot

模式1：驱动足1与动子紧密接触，在静摩擦力的作用下驱动动子向-x方向移动；此时，驱动足2与动子分离，并向+x方向移动。

模式2：驱动足1向-y方向移动，即将与动子分离；此时驱动足2向+y方向移动，即将与动子接触。

模式3：驱动足2与动子紧密接触，在静摩擦力的作用下驱动动子向-x方向移动；此时，驱动足1与动子分离，并向+x方向移动。

模式4：驱动足2向-y方向移动，即将与动子分离；此时驱动足1向+y方向移动，即将与动子接触。

整个过程完成后，驱动足1和驱动足2分别驱动动子实现-x方向的位移。

图6 V形双足式尺蠖电机运动平台Fig.6 V-shaped biped inchworm motor motion platform

反之，如果驱动模式按照模式4，3，2，1的顺序进行循环，驱动足1，2驱动动子产生反方向(x方向)的位移，模式循环顺序取决于驱动电压Ul，Ur的相位差。

4.2 实 验

4.2.1 实验平台搭建

通过SolidWorks等三维软件进行V形双足式尺蠖电机实验平台整体装配图的绘制。运动平台的三维模型与实物如图6所示。该平台主要包括电涡流传感器、动子导轨、双足定子、压力传感器、弹簧与手轮。通过调节手轮对双足定子施加一定的预紧力并通过压力传感器显示；双足定子施加驱动信号之后，驱动动子导轨运动，并通过激光干涉仪、电涡流传感器等得到动子导轨的运动位移、驱动速度等数据。

4.2.2 驱动方法实验验证

驱动电路系统产生驱动电压ua，ub，采用Fluke 190B对驱动电压进行实时观测。尺蠖电机驱动平台在驱动电压的驱动下运动，采用激光干涉仪进行步距测量，电涡流传感器IWFM 20U9501/S35进行驱动速度测量。

在无负载的条件下，固定母线电压Udc=150 V，驱动信号频率f=50 Hz，改变导通角α，在0°～180°内每隔5°进行取值，采用激光干涉仪、电涡流传感器测得对应的电机步距、驱动速度与其各自的理论值(式(28)、式(29))的对比曲线如图7和图8所示。

图7 步距与导通角的关系曲线Fig.7 Relation curve between step distance and conduction angle

图8 驱动速度与导通角α的关系曲线Fig.8 Relation curve between drive speed and conduction angle

由图7和图8可以看出，在一定允许误差范围内，实验结果满足前期理论推导，验证了驱动方法设计的合理性和可行性。同时发现当导通角α小于20°时，实验数据与理论值相差较大，其原因在于随着导通角的降低，驱动电压ua，ub的幅值减小，Δx，Δy减小，因此外界因素的影响逐渐显现出来。这些影响因素包括压电叠堆的非线性特性、外界的振动、定子与动子无法完全分离等。

4.2.3 电机最小步距实验

由于定子与动子的分离位移Δy、压电叠堆的非线性特性以及外界因素的限制，尺蠖电机存在最小步距。在无负载的条件下，固定母线电压Udc=150 V，驱动信号频率为0.5 Hz，导通角α从0°开始逐渐增大，采用激光干涉仪测得最小步距，引入导通角前后的最小步距对比曲线如图9所示。引入导通角后，最小步距由500 nm降低到330 nm，降低了34%。

图9 引入导通角前后最小步距对比曲线Fig.9 Contrast curves of minimum step length before and after introduction of conduction angle

4.2.4 电机最大驱动速度实验

由于压电叠堆的最大输出功率以及机械系统动态响应速度的限制，尺蠖电机存在最大驱动速度。在无负载的条件下，固定母线电压Udc=150 V，导通角α为180°，驱动信号频率f从0开始逐渐增大，得到引入导通角前后，尺蠖电机驱动速度与驱动信号频率f的关系对比曲线如图10所示，引入导通角前后，最大驱动速度均约为0.5 mm/s。

图10 引入导通角前后驱动速度与驱动频率的关系对比曲线Fig.10 Comparative curve of drive speed and drive frequency before and after introducing conduction angle

由图10可以看出，在一定允许误差范围内，当母线电压与导通角确定时，尺蠖电机驱动速度与驱动信号频率近似成线性关系。当驱动信号频率增大到一定程度(100 Hz)时，驱动速度达到最大值，之后驱动速度开始变小，这是由于机械系统，特别是各组柔性铰链结构的动态响应速度跟不上驱动信号的速度，执行器低频段的稳定性要高于高频段。

5 结 论

本文为了解决尺蠖电机高速和高位移分辨力难以兼备的问题，提出一种基于导通角调节的尺蠖电机驱动方法，引入新变量导通角α。首先介绍了尺蠖电机机电耦合模型的建立以及基于导通角调节的驱动方法，然后分析了V形双足式尺蠖电机的驱动机理，最后通过实验平台的搭建验证了驱动方法的合理性与可行性。实验结果表明：引入导通角后，最小步距由500 nm降低到330 nm，降低了34%；通过同时调节频率f和导通角α，可使电机具备0.5 mm/s的最大驱动速度和330 nm的最小步距的能力。