重组竹短期蠕变性能研究

孙丽惟，卞玉玲，周爱萍*，朱彦

(1.南京林业大学生物质材料国家地方联合工程研究中心，南京210037；2.无锡商业职业技术学院，江苏 无锡214153)

重组竹是将原竹沿顺纹方向疏解成疏松网状纤维束后，按顺纹方向组坯，经热压或冷压胶合而成的高强竹基复合材料[1-3]。随着其结构设计体系研究[4-6]的不断深入，已逐步应用于建筑结构主体。在正常使用条件下，结构材料将不可避免地因外界荷载及环境温湿度共同作用而产生蠕变。因此，明确重组竹在不同温度及应力水平下的蠕变性能对于重组竹结构体系的推广尤为重要。

蠕变一词由da C Andrade[7]于1910年提出，随后国外学者针对不同材料的蠕变进行了较为深入的研究，将蠕变分为瞬态蠕变、稳态蠕变及加速蠕变3个阶段，得到了典型蠕变曲线[8]。国内对于木材蠕变性能的研究起步较早，目前已形成了较为成熟的理论体系[9-10]。因竹、木材料具有相似的内部结构，故竹材蠕变性能的研究可参考木材。陈世英等[11]以竹材刨花板为研究对象，分析发现竹材刨花板的蠕变性能符合黏弹性理论。以Burgers模型为拟合依据，喻云水等[12]通过干湿两状态下的竹胶合板模板短期受弯蠕变试验，得出了竹胶合板模板在干湿两状态下的蠕变规律。涂道伍等[13-14]以毛竹为研究对象，分析了在不同应力水平、温度及含水率下毛竹横纹压缩蠕变特性，结果表明：当压应力在屈服极限以下时，毛竹横纹压缩蠕变三组分总量均与压应力、温度及含水率成正比，Burger模型用以拟合毛竹横纹压缩蠕变精确性较高。张晓敏等[15]综合考虑温湿度、含水率及竹节对毛竹径向压缩蠕变性能的影响，得出了不同温湿度条件下的蠕变规律。对于毛竹短期拉伸蠕变性能，闫薇等[16-17]以应力水平对其的影响进行了试验研究，确定了竹材短期拉伸蠕变中Burgers模型参数值。上述研究结果均表明，低应力水平下Burgers模型可很好地描述毛竹蠕变性能。李磊[18]和李玉顺等[19]分别对胶合竹及重组竹进行了长期蠕变性能研究，结果表明，Burgers模型在胶合竹梁的长期蠕变试验中拟合结果较为准确，而Findley模型在重组竹的长期蠕变试验中拟合结果较为准确。

上述研究主要局限于毛竹和竹材胶合板，对于类似重组竹材的蠕变性能研究相对较少，传统长期蠕变试验是将大型构件置于室外，采用单一加载方式(多为受弯)对其施加恒定荷载，缺乏同时具有重组竹拉、压、弯全面单轴受力方式的蠕变研究，且因简化了季节变化引发的温度波动等影响因素，得到的试验结果难以较好地反映实际情况。因此，笔者以重组竹小试件为研究对象，通过重组竹不同应力水平下24 h短期蠕变试验，得出蠕变应变-时间曲线及蠕变量-时间曲线，并以Burgers模型为基础，对其短期蠕变试验结果进行拟合。

1 材料与方法

1.1 试验材料

以江西省奉新县4年生毛竹经工业化加工的同批次重组竹材为试验材料，参照美国标准ASTM D143，综合考虑蠕变试验机内腔尺寸制备重组竹蠕变试件。每组应力水平设置3个平行试件，如图1所示。

图1 试件形状及尺寸示意图Fig. 1 Schematic diagram of specimen shape and size

1.2 试验设备与方法

选用深圳三思纵横50 kN微机控制电子蠕变持久试验机进行蠕变试验，产品型号为UTM5504-GD；选用量程为50 mm的Reliant引伸计进行变形测量。

对重组竹进行不同应力水平下的顺纹拉伸、压缩及弯曲试验。将温度和相对湿度统一调节为25 ℃和60%，拉伸、弯曲应力水平统一设置为15%，30%，60%及70%，压缩应力水平统一设置为15%，30%及60%，时间统一调节为24 h，以避免高温或高应力水平下试件因蠕变速率加快而中途破坏。每个试件在试验前预先按照目标温湿度置于环境箱中调置1 h。

对于顺纹受拉蠕变试验，由材性试验可得重组竹顺纹受拉极限强度ft=145.49 MPa，调节应力水平分别为15%ft、30%ft、60%ft及70%ft。

对于顺纹受压蠕变试验，由材性试验可得重组竹顺纹受压极限强度fc=102.36 MPa。调节应力水平分别为15%fc、30%fc及60%fc。

对于三点受弯蠕变试验，由材性试验可得重组竹三点受弯极限荷载Fb=561.36 N。调节荷载分别为15%Fb、30%Fb、60%Fb及70%Fb。

顺纹受压、顺纹受拉、三点受弯试验均分为加载和保载两阶段，加载阶段获得初始变形，保载阶段持续变形。顺纹受压和顺纹受拉试验采用引伸计测量其中部50 mm范围内的变形，三点受弯试验采用试验机作动器记录变形，由此绘制蠕变应变-时间曲线及蠕变量-时间曲线。

2 结果与分析

2.1 顺纹受拉蠕变结果

选取不同应力水平下的典型顺纹受拉蠕变应变-时间曲线，如图2所示。

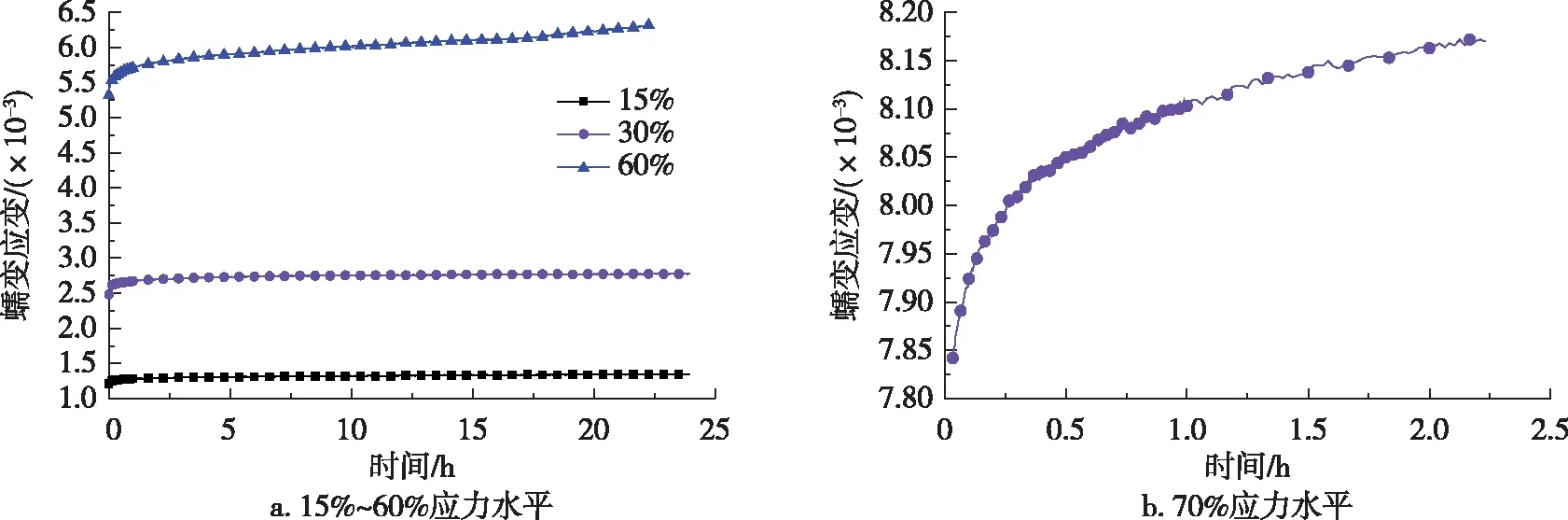
图2 顺纹受拉蠕变曲线Fig. 2 Creep curves of tensile along grain direction

由图2a可知，15%及30%较低应力水平下，蠕变应变-时间曲线走势相同，只包含瞬态及稳态蠕变2个阶段。15%应力水平下，重组竹初始蠕变应变为1.25×10-3左右，达到稳态阶段所用时间为2 h，2 h后材料进入变形稳定阶段，基本维持在1.30×10-3不变；30%应力水平下，重组竹初始蠕变应变为2.5×10-3左右，达到稳态阶段所用时间为3 h，随后基本维持在2.7×10-3左右。这表明较低应力水平下，重组竹初始蠕变应变及蠕变应变总量与应力水平呈线性正相关关系，达到稳态阶段后重组竹几乎不再发生变形及破坏，其内部细胞间孔隙、纤维及基体在历经初始变形后能够维持稳定，具有良好的抵抗蠕变变形的能力。60%应力水平下，材料虽未破坏，但曲线已具有加速蠕变趋势，说明较高应力水平下，重组竹蠕变不稳定性增强，抵抗蠕变性能有所降低。

由图2b可知，70%较高应力水平下，重组竹内部纤维先后发生断裂，最终仅在2.5 h内被拉断，破坏呈脆性断裂，说明较高应力水平对材料拉伸蠕变性能影响较大，使其表现出明显的破坏趋势。因此，较低应力水平下，重组竹拉伸抗蠕变性能明显优于较高应力水平，设计时应控制抗拉构件尺寸，确保其处于较低工作应力水平下，以利于其发挥自身抗蠕变性较高的优势。

2.2 顺纹受压蠕变结果

选取不同应力水平下典型顺纹受压蠕变应变-时间曲线，如图3所示。

由图3a可知，15%应力水平下，顺纹受压与顺纹受拉曲线趋势大致相同，仅包含瞬态及稳态蠕变2个阶段，初始蠕变应变为4.3×10-3左右，曲线斜率在0.1 h瞬态蠕变阶段内迅速减小，0.1～10 h逐步减小，10 h后趋于平稳；30%应力水平下，材料瞬态阶段变形量较大，达到稳态阶段的时间较长。

由图3b可知，60%较高应力水平下，材料表现出瞬态及稳态蠕变。试验后期曲线斜率迅速增加，变形急剧增大至破坏。不同于顺纹受拉试件，材料在顺纹受压时抵抗压力的时间较长，这是由于重组竹受压呈非线性，具有明显的破坏征兆，内部孔隙被不断压密，胶层开裂或纤维被逐步压溃直至与基体分离。对比顺纹受拉和顺纹受压两试验结果可知，重组竹抵抗受拉蠕变的能力较强，为降低其蠕变性能对结构的影响，在设计受压构件时，应尽量控制其处于较低应力水平。

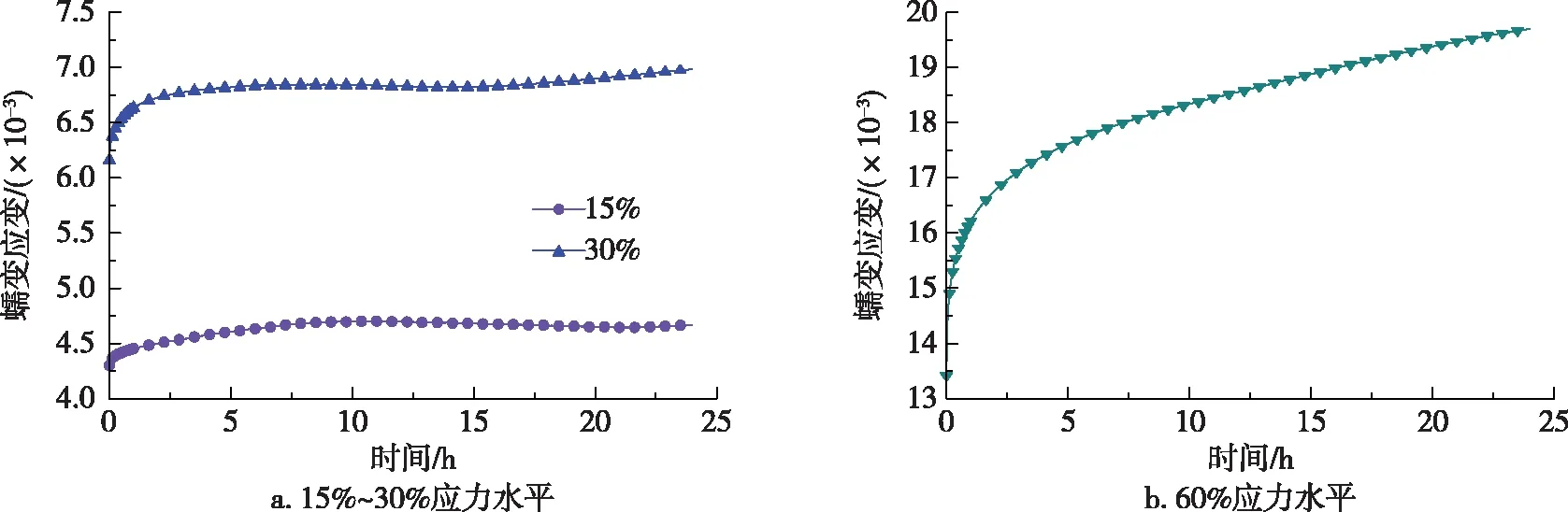
图3 顺纹受压蠕变曲线Fig. 3 Creep curves of compression along grain direction

2.3 三点受弯蠕变结果

选取不同应力水平下典型三点弯曲蠕变量-时间曲线，如图4所示。

由图4a可知，15%及30%较低应力水平下，蠕变量-时间曲线走势较为平缓，仅包含瞬态及稳态蠕变2个阶段。15%应力水平下，重组竹初始蠕变量为2.91 mm，约0.5 h后达到3.03 mm，随后维持在3.0 mm左右直至试验结束；30%应力水平下，重组竹初始蠕变量为5.88 mm，约为15%时的2倍，约0.5 h后达到6.13 mm，随后维持在该值直至试验结束。由此可知，较低应力水平下，重组竹初始蠕变量与应力水平呈正比，且具有较好的抵抗蠕变变形能力。相比较低应力水平，在60%应力水平下，曲线已具有加速蠕变趋势，即较高应力水平下，重组竹蠕变不稳定性增强，抵抗蠕变的能力有所降低。

图4 三点受弯蠕变曲线Fig. 4 Creep curves of three-point bending

由图4b可知，70%较高应力水平下，重组竹表现出瞬态、稳态及加速蠕变3个阶段。4.2 h左右曲线斜率迅速增加，试件跨中变形急剧增大，下部纤维先后断裂直至破坏。与顺纹受拉及顺纹受压不同，重组竹在三点受弯情况下，具有较高的蠕变初始量。对比较高应力水平下3种加载方式的蠕变曲线可知，顺纹受压蠕变曲线的第3阶段时间最长，三点受弯次之，顺纹受拉最短，这与其最终的破坏形式有关。

3 模型验证

3.1 Burgers模型简介

Burgers模型[8]是一个由Maxwell模型及Kelvin模型串联组成的四元件力学模型，能较好地描述重组竹材料的黏弹性行为，如图5所示。

η1和η2分别为黏性元件的黏性系数；E1和E2分别为弹性元件的弹性模量。图5 Burgers模型Fig. 5 Burgers model

该模型的本构方程为：

σ+p1σ+p2σ=q1ε+q2ε

(1)

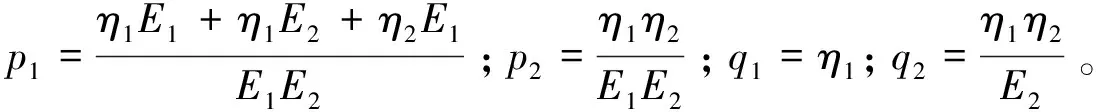
将式(1)作Laplace变换，当t=0时，可得：

(2)

式中：ε(t)为应变；σ0为保载阶段的应力值。当应力不变时，Burgers模型可转化为：

ε(t)=A+B(1-e-Ct)+Dt

(3)

式中：A为瞬时弹性变形；B为延迟弹性变形；C为黏弹系数；D为黏性系数。A和D可反映弹性形变和黏性形变；B和C可反映黏弹性形变。

3.2 模型拟合曲线

3.2.1 顺纹受拉蠕变模型拟合

基于Burgers模型的重组竹短期顺纹受拉蠕变曲线拟合结果及拟合参数如图6及表1、2所示。

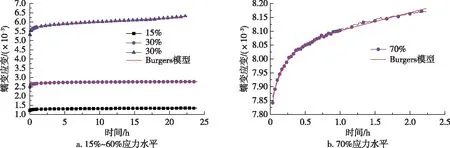
图6 顺纹受拉蠕变拟合曲线Fig. 6 Creep fitting curves of tensile along grain direction

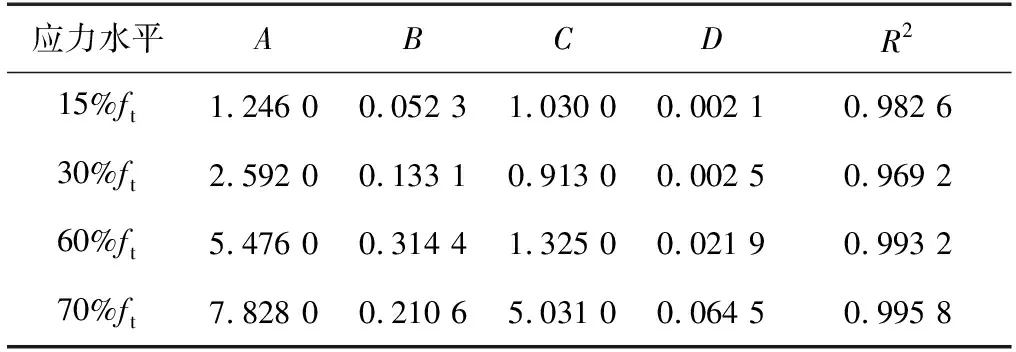
表1 不同应力水平顺纹受拉蠕变拟合参数结果Table 1 Creep fitting parameters of tensile along grain direction at different stress levels

表2 不同应力水平顺纹受拉不同部分蠕变值Table 2 Creep values of different parts of tensile along grain direction at different stress levels %

由图6及表1可知，对于只具有瞬态及稳态蠕变阶段的重组竹受拉蠕变试验，Burgers模型拟合所得曲线与试验曲线趋势相同，拟合决定系数(R2)均在0.96～1.00，能够与试验结果良好吻合。将表1中的参数代入式(3)可得各对应情况下的蠕变量，如表2所示。由表2可知，对于顺纹受拉试验而言，重组竹蠕变总量、弹性应变及黏性应变均随应力水平的升高而增大，说明应力水平的升高会对重组竹受拉蠕变产生不利影响。

3.2.2 顺纹受压蠕变模型拟合

基于Burgers模型的重组竹短期顺纹受压蠕变曲线拟合结果及拟合参数如图7及表3、4所示。

由图7及表3可知，参数A随应力水平的升高而变大，即应力水平越高，蠕变变形量中的弹性变形越大，弹性应变与应力水平基本呈线性关系。对于只具有瞬态及稳态蠕变阶段的重组竹顺纹受压蠕变试验，Burgers模型拟合所得曲线与试验曲线趋势相同，拟合决定系数均在0.96～1.00，能够与试验结果良好吻合。将表3中的数据代入式(3)可得各组分蠕变值，如表4所示。由表4可知，重组竹弹性应变、黏弹性应变、黏性应变及蠕变总量均随应力水平的升高而变大，说明较高应力水平会增加重组竹材的蠕变量，产生不利的影响。

图7 顺纹受压蠕变拟合曲线Fig. 7 Creep fitting curves of compress along grain direction

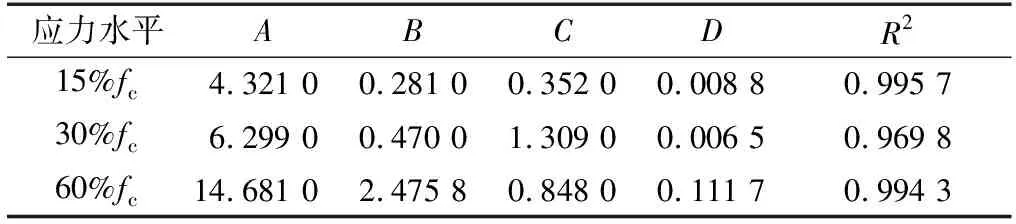
表3 不同应力水平顺纹受压蠕变拟合参数结果Table 3 Creep fitting parameters of compress along grain direction at different stress levels

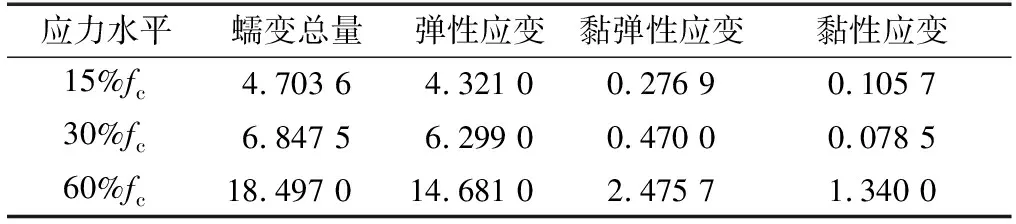
表4 不同应力水平顺纹受压不同部分蠕变值Table 4 Creep values of different parts of compress along grain direction at different stress levels %

3.2.3 三点受弯蠕变模型拟合

基于Burgers模型的重组竹短期三点受弯蠕变曲线拟合结果及拟合参数如图8及表5、6所示。

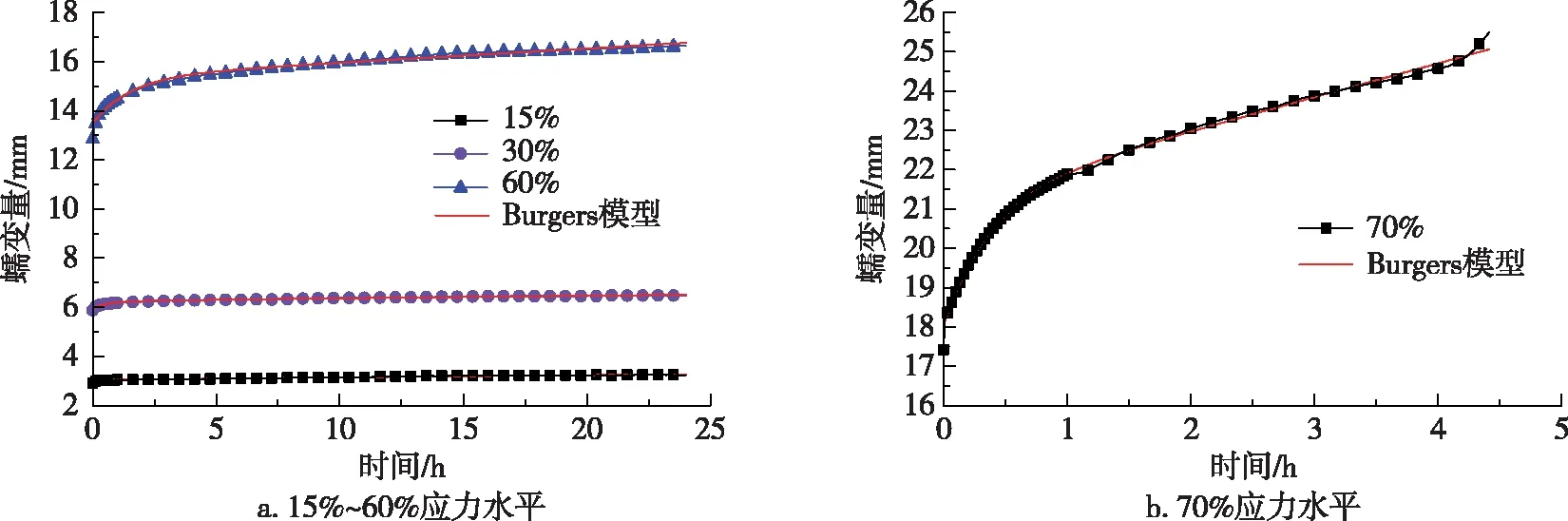
图8 三点受弯蠕变拟合曲线Fig. 8 Fitting curves of three-point bending creep

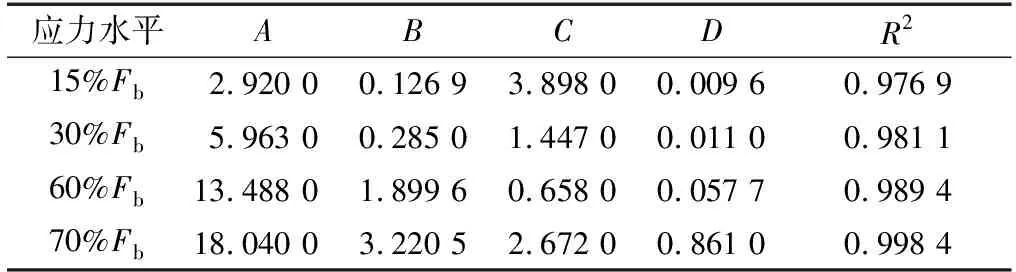
表5 不同应力水平三点受弯蠕变拟合参数Table 5 Creep fitting parameters of three-point bending at different stress levels

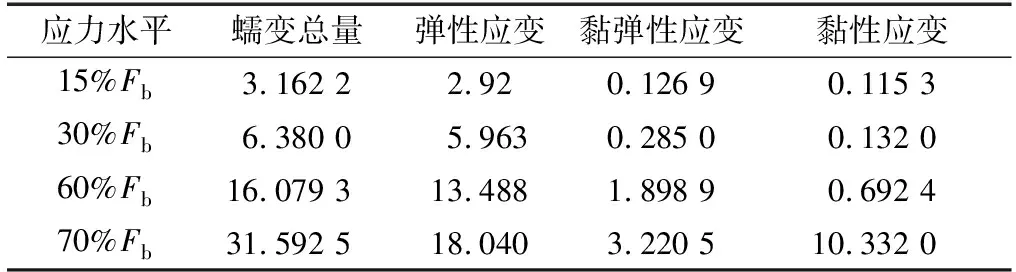
表6 不同应力水平三点受弯不同部分蠕变值Table 6 Creep values of different parts of three-point bending at different stress levels %

由图8及表5可知，对于只具有瞬态及稳态蠕变阶段的重组竹三点弯曲蠕变试验，Burgers模型拟合所得曲线与试验曲线趋势相同，拟合相关系数均在0.97～1.0，能够与试验结果良好吻合。将表5中的数据代入式(3)可得各组分蠕变值，如表6所示。由表6可知，三点受弯蠕变试验中应力水平对重组竹弹性应变、黏弹性应变及黏性应变3个部分蠕变值及蠕变总量的影响规律与顺纹受拉和顺纹受压蠕变相同，黏弹性形变均随应力水平的升高而增大。

4 结 论

1)温湿度一定时，对于顺纹受拉、顺纹受压、三点受弯试验，在较低应力水平下，蠕变只包含瞬态及稳态蠕变2个阶段，初始蠕变应变及蠕变应变总量与应力水平呈线性正相关关系，达到稳态阶段后重组竹几乎不再发生变形及破坏，具有良好的抵抗蠕变变形的能力。在较高应力水平下，重组竹蠕变不稳定性增强，抵抗蠕变性能有所降低，设计时应控制构件尺寸，确保其处于较低工作应力水平下，以利于其发挥自身抗蠕变性较高的优势。

2)对比顺纹受拉、顺纹受压、三点受弯3种受力情况，顺纹受拉破坏呈脆性，无明显的破坏征兆，顺纹受压、三点受弯均具有一定的破坏征兆。在较高应力水平下，顺纹受压蠕变曲线第三阶段时间最长，三点受弯次之，顺纹受拉最短。

3)Burgers模型对于仅包含瞬态及稳态蠕变阶段的重组竹短期蠕变性能拟合程度较高，拟合决定系数均为0.96～1.0，能够较好地表现重组竹短期蠕变性能。重组竹蠕变总量、弹性应变及黏性应变均随应力水平的升高而增大。