矩形小翼不同排列方式换热特性研究

(华北理工大学 冶金与能源学院，河北 唐山 063210)

随着时代的进步与发展,当今社会各种样式的热交换设备在建筑、能源、化学、金属提炼、航天等工业方面大量使用。但传统的换热设备存在换热效率较低，造成一定的资源浪费现象,只有逐步加强热交换设备的使用效率,才能提高能源转换效率，减轻能源浪费和材料短缺现象。因此，需要不断开发出各种新的换热方法实现热交换效率的提高。

研究过程通过对湍流流动下流体在加装矩形小翼的通道的流动的换热特性开展模型设计及数值研究,比较矩形小翼在不同排列布置方式下不同的换热特性,并提出换热特性良好的攻角和排列方式,为矩形小翼在不同方式下的换热特性的研究与技术的改良提供了一定量的数据参考。

1 物理模型的建立与数据处理

通过Gambit进行物理模型的建立，采用Fluent数值模拟进行计算，从而得到攻角对换热性能的影响。研究过程中选择顺排、错排、V形排列三种排列方式，截取通道的不同截面来研究相应的速度、温度、压力等云图和流动轨迹图，得出不同攻角下数据并作Nu-Re、f-Re、JF-Re折线图研究讨论，得到攻角对换热性能的影响，并优化攻角的换热。在不同的攻角中，选取换热效果较好的角度，对其进行排列方式的优化，找出相同攻角下最佳的排列方式，选出较优秀的方案。

1.1 物理模型的建立

根据曾卓雄[2-5]等学者的研究发现，确定在60°时顺排的换热情况最佳，因此，研究过程首先进行大量研究在顺排情况下，矩形小翼不同的角度排列的换热情况，大致角度范围定在30°～75°，每15°为一个单位量，如何进行验证，并研究出在60°的情况下错排、顺排、V型排列那个更佳。大致确定的数据如表1所示。V形通道尺寸大致数据如表2所示，L、W、H为矩形通道的长、宽、高,m、n为横、纵向间距，为攻角，l、w、h为矩形小翼的长、宽、高(其中a为两对小翼之间的间距)。

表1 通道1基本数据

表2 通道2基本数据

1.2 数学模型

1.2.1 控制方程及边界条件

(1)

动量方程：

(2)

能量方程：

(3)

方程的求解模型采用RNGk-ε湍流模型，用于确定湍动能k和湍动能耗散率ε的控制方程为[6]

(4)

(5)

式中：C1ε、C2ε、σε及σk为常数项；Gk表示平均速度梯度产生的湍流动能。此外，RNGk-ε模型中还引入了不同于标准k-ε模型的湍流黏度计算公式：

(6)

流经通道的干空气密度ρ=946.2 kg/m3，黏度μ=2.19×10-5Pa·s，导热系数λ=0.321 W/(m·K)，等压比热容cp=1 022 J/(kg·K)，水在圆管进口处的速度范围定为3～10 m/s，有公式

(7)

式中：ρ为水的密度，g/m3；v为水在圆管进口处的速度,m/s；Dv为通道进口截面的当量直径；μ为水的黏度[7]。

通过式(7)可得，不同速度下的雷诺数和湍流强度结果如表3所示。

表3 不同速度下的雷诺数和湍流强度

1.2.2 数据处理

雷诺数Re的定义为

(8)

式中：v为通道进口截面的平均速度；Dv为通道进口截面的当量直径；μ为通道空气的运动黏度。

通道壁面的局部表面传热系数定义如下

(9)

式中：qw为壁面局部热流密度,kg/m3；Tw为壁面的温度，K；Tf为冷却气体的平均温度，K。

局部努赛尔特数Nux:

(10)

平均努赛尔特数Num:

(11)

换热因子j定义为

(12)

阻力因子f定义为

(13)

式中：Δp为进出口压差，Pa；L为通道长度，m；ρ为流体的密度，kg/m3。

综合性能评价标准为

(14)

2 计算结果对比分析

2.1 攻角对流动换热性能的影响

为了验证所采用的数据模型可靠，分别从攻角、排列方式、两个方面进行研究，研究各自对通道换热性能的影响。首先，对攻角展开进一步的讨论和流动传热的细节分析。由于物理模型在结构上的周期性重复，为了能够展现局部并且节省计算空间只给出了两排的小翼分布情况。

2.1.1 角度的优化

如图1所示，由光滑通道与加装矩形小翼的通道相比，加装矩形小翼的通道的传热能力明显提高，冷却速度增加的区域主要为小翼周围，可见矩形小翼区域的传热增强是由于小翼的阻挡带来的特殊流动所改变的。因此分别选取加装攻角为30°、45°、60°、65°、75°和90°的矩形小翼在通道内的计算结果进行对比分析。

图1 矩形通道内的温度变化

图2为在顺排的工况下，攻角为变化值，在攻角为30°、45°、60°、65°、75°、90°的通道的换热面努塞尔数分布。由于攻角的度数不同使得换热面积及传热系数发生了变化。6种通道在相同工况下的小翼表面的努塞尔数Nu/Nu0，如图2所示。从图2中可看出：30°、45°、60°、75°努塞尔数非常接近，攻角为60°、75°的通道努塞尔数大于其他2种，在雷诺数小于5 000时，攻角为60°时换热效果最佳，当雷诺数大于5 000时，攻角为75° 的努塞尔数略大于攻角为60°，差值不超过2%。

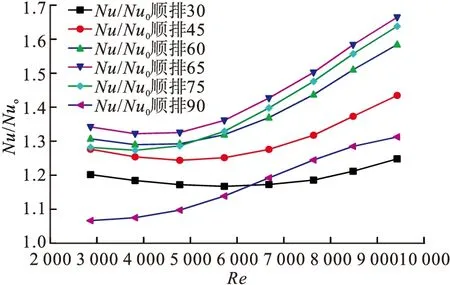
图2 相同工况下不同攻角下的通道换热面Nu/Nu0分布

为了研究出矩形小翼综合对流换热流动性能相对较佳的攻角，进一步对矩形小翼攻角为90°时通道的换热面努塞尔数进行求解，可以看出攻角为90°时换热情况远低于攻角为75°时，所以矩形小翼综合对流换热流动性能与攻角并非线性关系，加装攻角为75°，在雷诺数大于5 000时矩形小翼综合对流换热流动性能相对较佳。

在进一步研究出矩形小翼综合对流换热流动性能相对较佳的攻角，进一步对矩形小翼攻角为65°时通道的换热面努塞尔数进行求解。并对加装攻角为65°的矩形小翼的矩形通道进行实验分析。

如图3所示阻力因子f反映的是矩形通道内的阻力特性，阻力因子的值越大，表面流体在流动过程中所消耗的功就更大。图3所示为不同攻角的Re-f图像，对不同攻角进行了比较。通过不同方式f的比较可看出，虽然攻角65°时的换热性能表征系数Nu大于其他攻角度数，但其阻力因子并不是最小的，f的大小随着攻角度数增大而增加明显程度约为1%～5%。

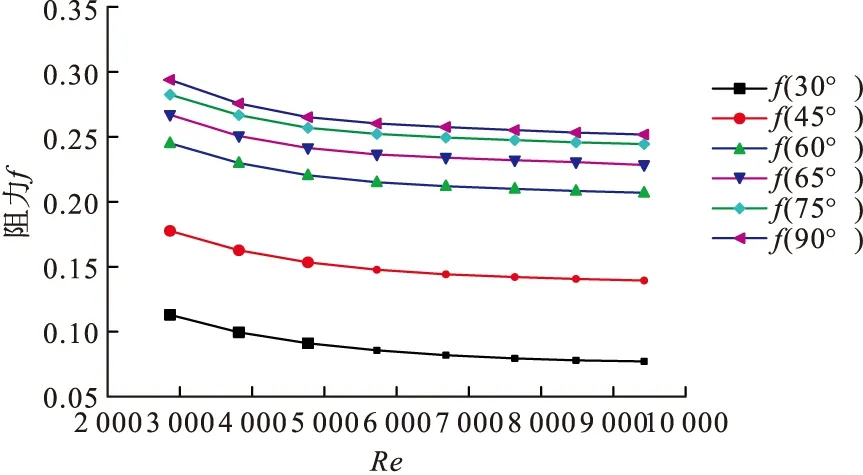
图3 不同雷诺数下的阻力比较

当具有相同雷诺数时，换热因子j和阻力因子f均随着攻角的增大而增大，随着雷诺数的增加而减小，最终都趋于稳定。不能判定哪种角度换热效果最好，只能通过综合性能来判断，从图4可以看出：综合性能JF最好时对应的矩形小翼的攻角为65°。

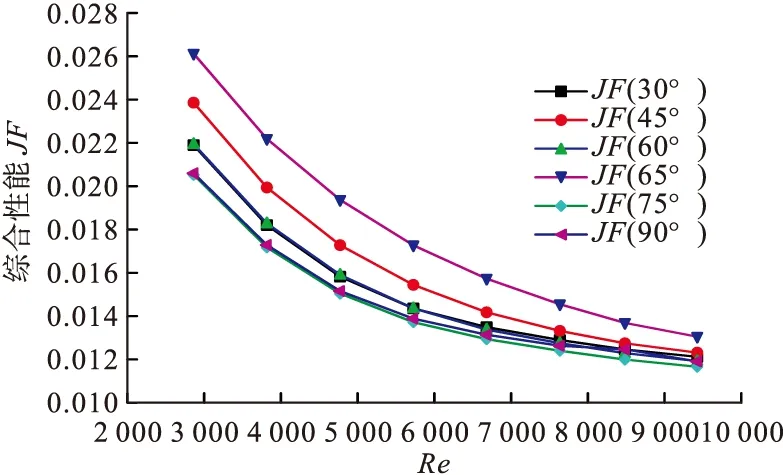
图4 不同雷诺数下的综合性能

得出如图2所示结果，无论雷诺数为何值换热,情况均好于60°和75°。且本身在不同雷诺数下呈线性增长趋势，因此在相同工况下矩形小翼的攻角为65°时，换热效果最佳。

2.1.2 速度场分析

图5为速度在6 m/s时不同攻角下矩形小翼周围的速度变化，由不同攻角的纵向截面速度矢量图可以看出，随着矩形小翼攻角的增大，小翼周围的速度减小的面积区域越来越大，观察图5中的变化，小翼周围的速度减小，说明流体流经通道受到了阻力的影响，且随着攻角的变大，通道的阻力也增大。因此，加装矩形小翼是阻力因子产生的原因。

图5 不同攻角下的速度矢量图

2.1.3 压力场的分析

流体的入口速度为6 m/s的工况下，不同攻角下的压力分布如图6所示，图中矩形截面左侧为流体入口，右侧为流体出口，观察6种不同攻角下的压力分布对比图，根据整体的压力分布图可以看出：压力的大小随着流动方向而逐渐减小，进出口压力的存在，是流体克服摩擦阻力进行流动的主要原因。不同攻角的压力损失相比，攻角的增大会引起压力损失的变大，也就是说都是由于流动阻力的增加而引起的。这说明传热性能的增强都是以流动阻力的增加而变化的。

图6 不同攻角下的压力云图

2.2 排列方式对流动换热性能的影响

2.2.1 排列方式的比较

图7～图9是不同攻角的矩形小翼在不同排列方式下的换热情况，主要针对攻角为45°、60°、75°时的顺排及错排的流动换热，得到的努塞尔数比Nu/Nu0(Nu0为光滑通道静止时的努塞尔数)，通过折线图可以得出：

(1)无论是何种攻角、何种排列方式下，当雷诺数不同时，努塞尔数比均大于1，说明不论在什么情况下，矩形小翼结构的引入使得通道换热面Nu/Nu0明显提高，小翼的强化传热效果明显增强。随着Re的增加,各种方案Nu/Nu0均近似线性增加。

(2)无论何种攻角，矩形小翼结构的引入使得通道换热面Nu/Nu0明显提高，小翼的强化传热效果明显增强。随着Re的增加,各种方案Nu/Nu0均近似线性增加；在Re相同时,顺排小翼的Nu/Nu0相比于对应的错排小翼传热效果明显，差值不超过2%。

(3)两种不同排列方式的换热器综合性能JF随雷诺数的变化情况与基本结构相比有所降低，且随着雷诺数的增加而减小，由于阻力的产生使加装小翼的矩形通道换热综合性能比光滑通道要低。

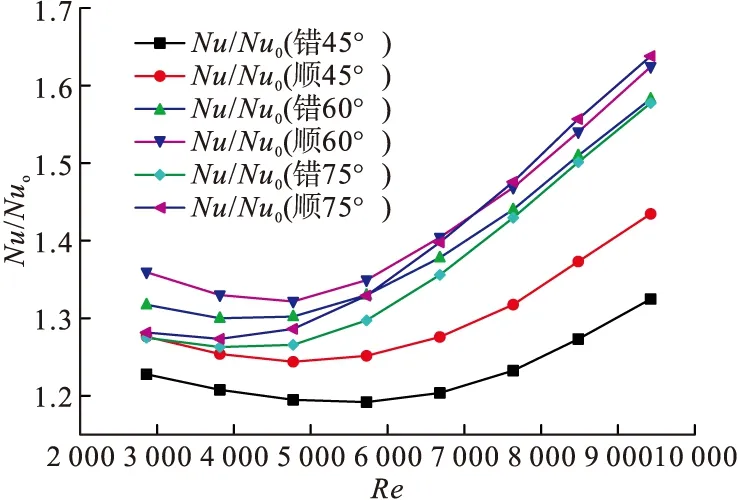
图7 相同工况下不同排列方式及不同攻角小翼通道换热Nu/Nu0面分布

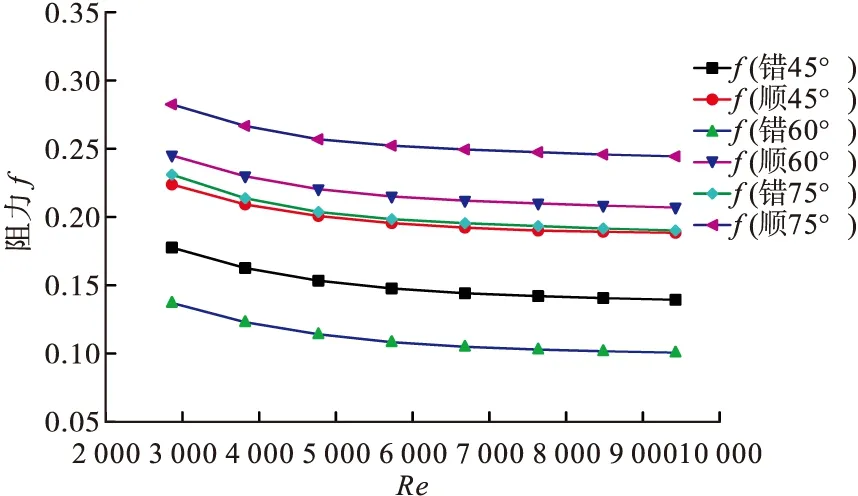
图8 不同排列方式不同攻角的阻力比较

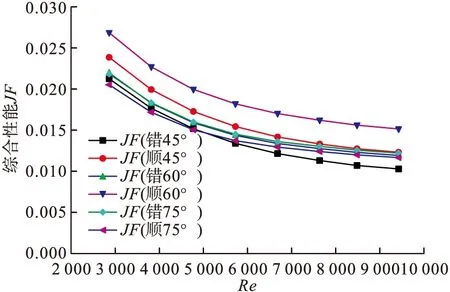
图9 综合换热性能的比较

因此接下来在顺排60°的相同条件下，采用不等间距(间距分别为25、35、45、55)的排列方式，来比较相同工况下的不同排列方式的换热情况。得到数据如图10所示。明显不等间距排列方式的换热情况优于错排及顺排。

其综合性能同样由换热因子j及阻力f所决定，错排、顺排、不等间距排列的换热因子基本相同，不等排列的在数值上稍微大一些，图11表明三者的阻力系数却是顺排>不等间距>错排，充分说明交错排列所产生的阻力小，但换热因子不如顺排及不等排列，因此导致结果如图12所示，不等间距排列的综合换热性能更好，雷诺数更高，换热效果更优异。

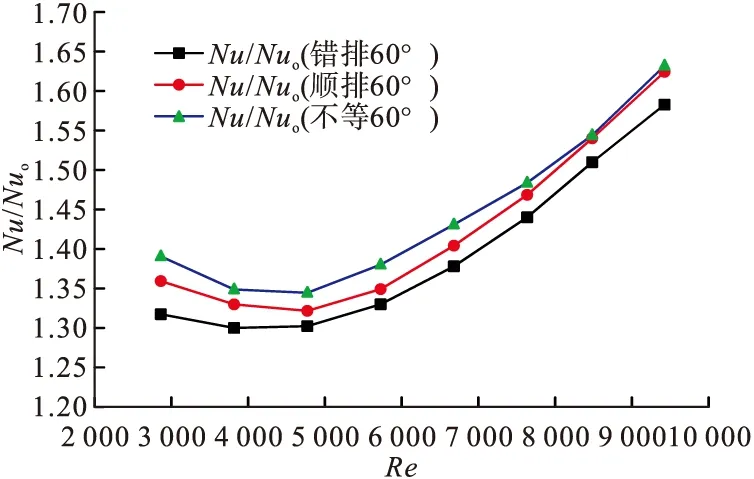
图10 相同工况下不同排列方式小翼通道换热面Nu/Nu0分布

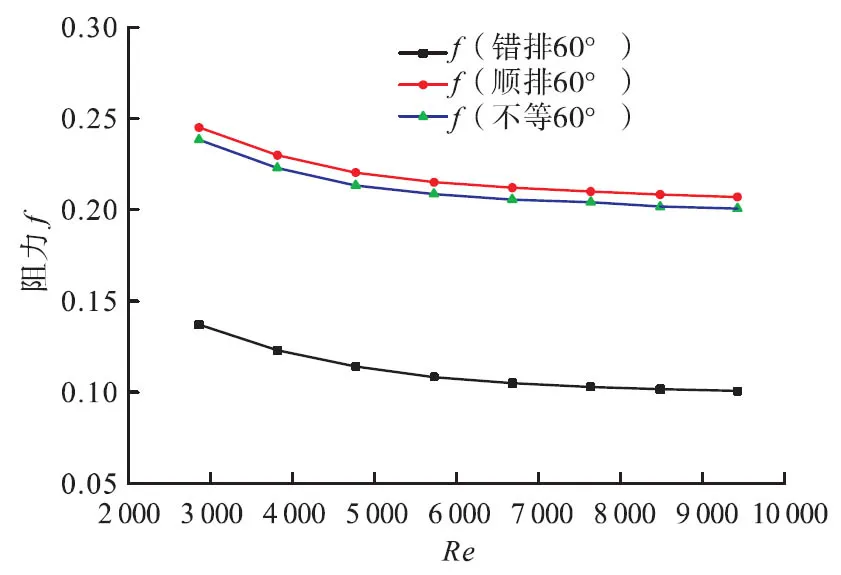
图11 相同工况下不同排列方式的阻力

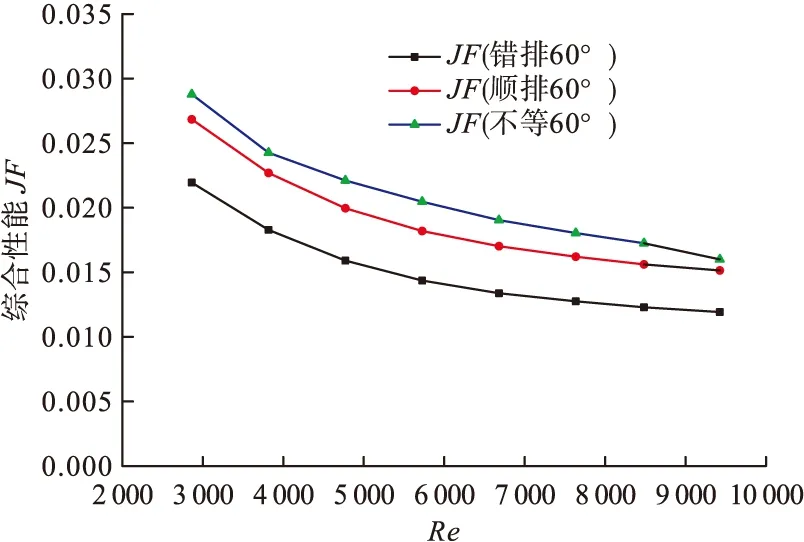
图12 相同工况下不同排列方式的综合换热性能

为了比较V型排列与“一”字型排列的优越性，采用不同的模型，选取比较宽敞的通道进行V型排列，采用同样介质流过通道，进行同样的Fluent计算，得到图13的结果。

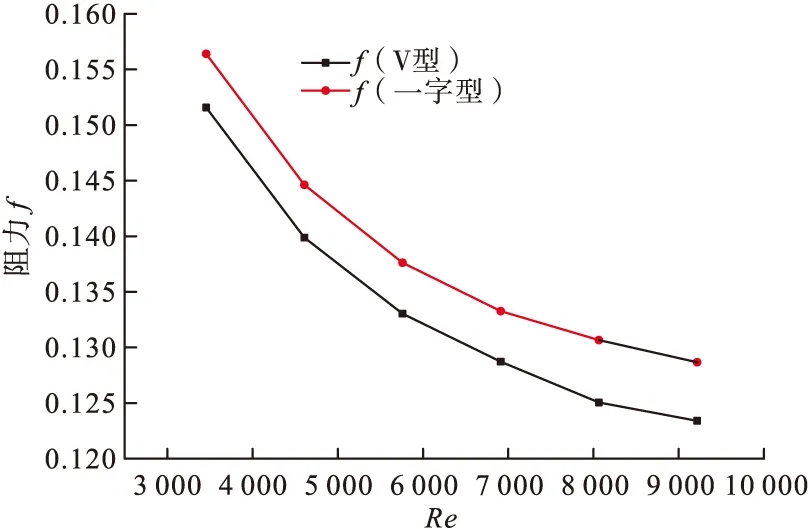
图13 相同工况下不同排列方式的阻力

如图13所示，由于通道比较宽敞V型排列阻力相比于“一”字型排列阻力较低，如图14所示，因此“一”字型排列的换热情况要比V排列方式的换热效果要好。“一”字形排列的努赛尔数高于V型1%。而图15中综合换热性能两种排列方式基本相同，差距很小。

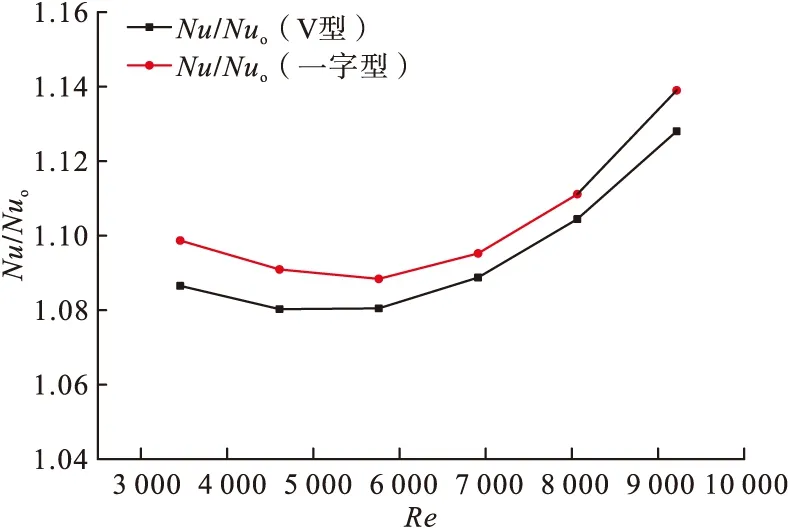
图14 相同工况下不同排列方式小翼通道换热面Nu/Nu0分布

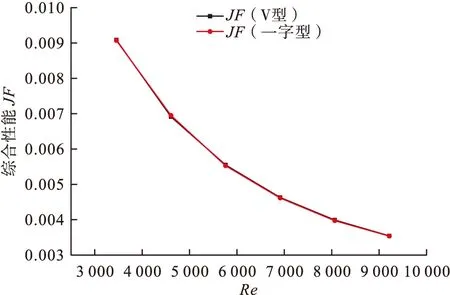
图15 相同工况下不同排列方式的综合换热性能

2.2.2 沿程分析

图16给出了Re=5 727.3 ，矩形小翼个数为5对时，垂直于X轴方向截取210个截面(坐标分别为X1=-105、X2=-104、X3=-103……X108=103、X209=104、X210=105等截面)的努赛尔分布图。由于进出口截面比较特殊，不放在计算结果内。

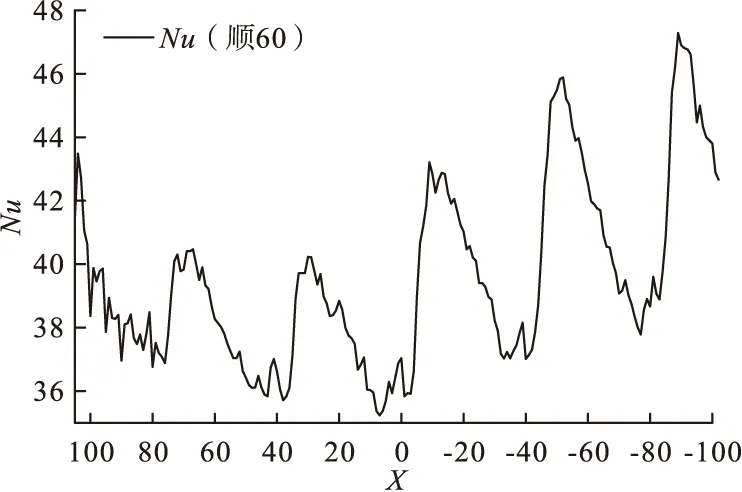
图16 矩形通道的沿程Nu分布

由图16可得，随着流动的进行，横截面上的温度逐渐降低，而努赛尔数逐渐升高，但在升高的过程中流体被温度较低的壁面小翼冷却。在安装矩形小翼的地方，由于矩形小翼的存在，产生一定的阻力而导致在小翼处的努赛尔增长缓慢，在小翼周围努赛尔数先增加在减小，且增加的幅度越来越大，与光滑通道相比，加装矩形小翼的通道沿程的换热效果均比光滑通道高，结果如图17所示。

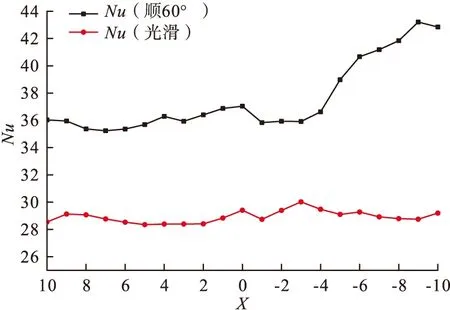
图17 沿程局部努赛尔数的对比

顺排方式排列在坐标为0处是小翼的尾部，从图17中可以看出，在流体通过效益的阻力后，努赛尔数迅速增加，一定距离后，努赛尔数开始逐渐降低，因此再来观察错排与顺排相比。经过截面以及计算，得到结果如图18所示。

顺排时在0处有一对小翼，而错排在0处只有单个小翼，经过小翼后顺排的努赛尔数超过错排的努赛尔数，其换热情况反而超过了错排方式，说明一对小翼所影响的换热效果要比单个小翼的换热效果好。

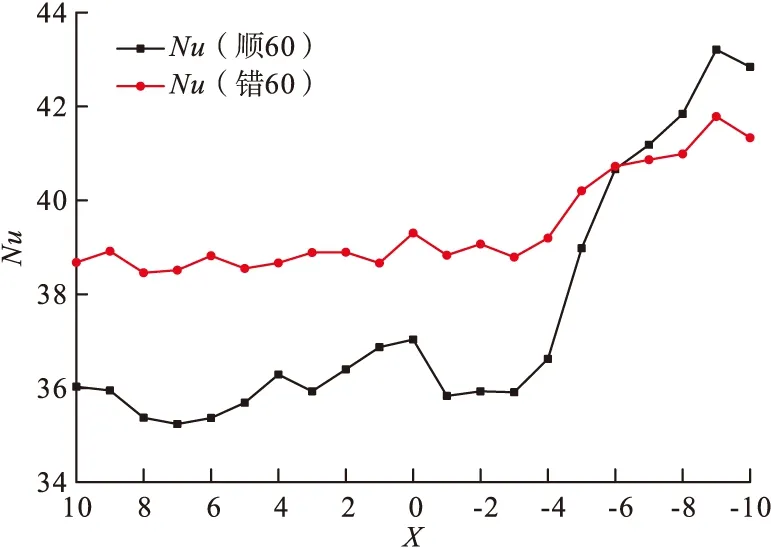
图18 不同排列方式沿程的局部比较

2.2.3 温度分析

在宽敞通道中，“一”字型排列的温度变化与V型排列温度变化相比温差较明显，出口温度更低一些，因此换热情况的比较中，“一”字型排列的努赛尔数更高(见图19)。

3 结 论

研究应用Gambit及Fluent软件对加装矩形小翼的矩形通道内的流动换热性能的影响进行了数值模拟分析，分别计算矩形小翼不同攻角和排列方式下矩形通道内的速度场、压力场和温度场。得到不同雷诺数下加装矩形小翼矩形通道的阻力、换热因子和换热曲线，并比较分析了模拟和实验的结果，验证了模拟的可靠性主要从努塞尔数Nu、阻力因子f、换热因子j及综合换热性能JF等性能系数进行换热性能的分析，主要结论如下：

(1)具有矩形小翼的矩形通道流动和传热性是周期性波动的，在加装矩形小翼的部分换热能力最强，光滑部分换热能力较弱，所以具有矩形小翼的矩形通道的换热比光滑通道得换热能力强。

(2)通过加装不同攻角的矩形小翼的通道换热情况对比，可发现：随着矩形小翼攻角的增大，换热通道的回流区面积逐渐减小。攻角为65° 的矩形通道，在不同的雷诺数下，努塞尔数呈线性增长，大于其它攻角下的努塞尔数，通道内的阻力随着攻角的增大而增大，综合换热性能在攻角为65° 时呈现最佳状态。

(3)在不同排列方式下，从数值模拟结果的观察分析可得出，顺排的换热性能优于错排，不等间距排列方式优于顺排、错排。

(4)宽敞的通道情况下，可以采用V 型排列与“一”字型排列方式的比较，研究表明，“一”字型排列的换热情况优于V型排列。

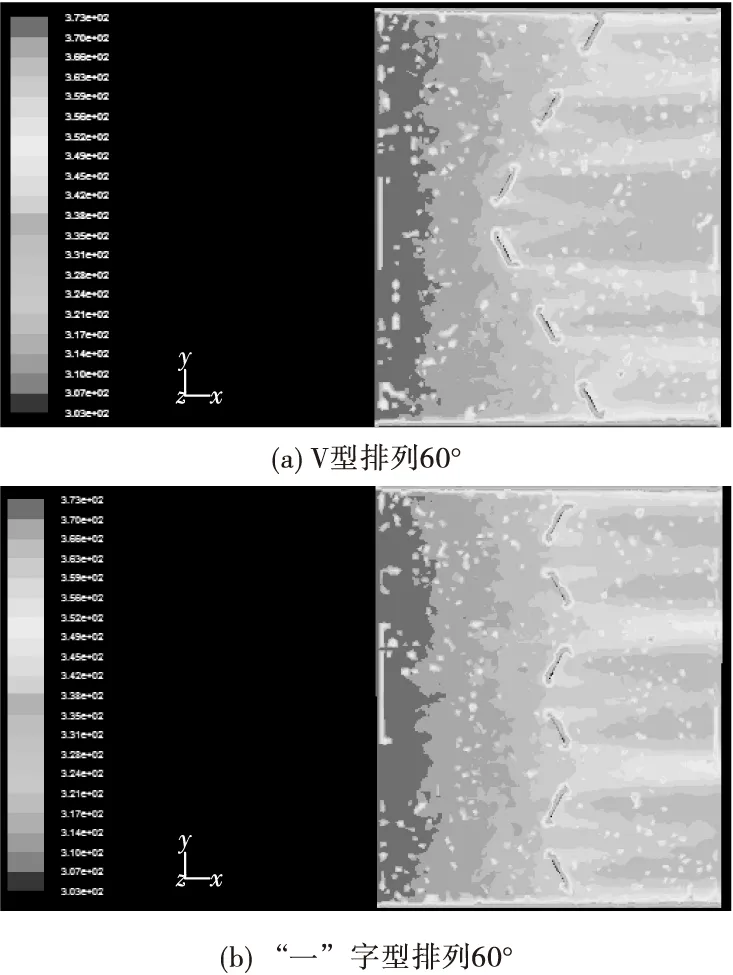
图19 不同排列方式下的温度变化