集装箱码头泊位—堆场资源的鲁棒性模板决策

韩笑乐，许 可，陆志强

(同济大学 机械与能源工程学院，上海 201806)

0 引言

随着经济全球化的发展，集装箱码头在全球经济中的地位日趋凸显，为加快集装箱码头的工作效率，提升各国集装箱码头的吞吐能力，近年来，大批学者针对集装箱码头中的各项问题展开了具体研究，Bierwirth等[1-2]和Carlo等[3]对这些研究进行了总结与归纳。通常，集装箱码头相关决策根据作业区域的不同，分为海侧、堆场和陆侧3类问题。而根据集装箱的中转与转运比例不同，也可将集装箱码头分为中转港与进出口港两类，二者的区别主要在于对集装箱的处理，前者中集装箱需在船舶之间进行转运，主要考虑转运时的总距离和堆区分配问题，后者中集装箱需在船舶到达前和离开后对堆场进行较长时间的占用，其停留时长也与闸口的能力相关，故考虑较多的是堆场的容量与闸口能力问题。就笔者所知，目前各类文献研究都集中在中转港，而对于进出口港的研究较少。中国作为世界港口大国，其港口主要为进出口港，各种问题亟待研究和探讨，基于此，本文将问题的研究背景设为进出口港。

对于海侧、堆场和陆侧问题，已有大量文献分别针对它们展开了研究，主要涉及到的资源包括泊位、岸桥、堆场、场桥、集卡和闸口等。其中，泊位与堆场作为两大最主要的固定资源，在集装箱码头一旦建成后，就难以像岸桥、堆场、集卡和闸口等资源一样可以重新添置或扩建，因此二者的容量往往成为制约码头效率的关键因素，而在实际调度中，这两类资源存在相互制约的关系，一方面，只考虑泊位分配问题，当出现堆场资源不够的情况时，泊位分配的结果也就失去了意义；反之，只考虑堆场容量问题，则可能出现不能满足泊位的情况。因此，二者必须同时考虑，才能满足船舶在集装箱码头的真实调度情况。随着研究的深入，许多学者开始考虑到二者联合调度的必要性，对此，Zhen等[4]针对BAYAP(Berth allocation and yard allocation problem)，提出一个混合整数非线性规划模型，并对该模型进行了线性化处理，在此基础上，提出一个三阶段启发式算法规则，最后通过仿真算例，验证了算法在大规模真实环境中的有效性；Ma等[5]对文献[4]模型进行了改进，提出了基于有向邻域搜索(guided neighborhood search)的启发式算法，并与临界摇摆邻域搜索算法(critical shaking neighborhood search)及传统方法改进后的实用算法进行了对比；Liu等[6]以最小化超出时间窗量和最小化运输距离为目标，建立了双目标的数学模型，在带精英策略的快速非支配排序遗传算法(fast elitist Non-dominated Sorting Genetic Algorithm, NSGA-Ⅱ)算法框架的基础上提出了进化算法。

另一方面，许多学者开始意识到模板计划对于集装箱码头的重要性，一个相对固定的作业调度可以为船舶公司及码头有效地降低因每个周期的作业不同所带来的成本及给其他船舶造成的影响。对此，Moorthy[7]首次提到了泊位模板和堆场模板的概念，他们以船舶到达后两小时内能开始作业的比例和中转箱运输成本为目标，提出一个基于序列对的模拟退火算法；此后，Zhen等[4]、Ma等[5]、Liu等[6]在考虑泊位堆场联合调度问题的同时，同样考虑了模板计划的问题；Hendriks等[8]也同样，在集装箱的到达和离开时间给定的情况下，以集装箱运输距离最小化为目标，提出一个启发式算法并得到了局部最优解，同时提出一个算法来选择合适的初始点，最后用安特卫普提供的真实数据进行了实验，并与经典方法进行了对比，证明了算法的有效性；Jin等[9]在Hendriks等[8]提出的混合整数规划模型的基础上，考虑周期性船舶的靠泊位置，母船与支线船舶之间转运的堆场位置，以及支线船舶的开始时间调度模板这3个决策问题，将模型转换为集覆盖模型，并使用列生成的方法对该问题进行了求解。

而在进行模板计划决策时，另一个重要的因素，即不确定性也必须被考虑。由于在实际调度决策过程中，存在着来自各方面不确定因素的干扰，导致船舶无法按预定的计划进行作业，这不仅会影响该船本身，还会影响其他船舶的调度，甚至导致模板计划变得不可行。因此，一个针对不确定性的调度方案是行之必要的。Zhen等[10]考虑船舶到港时间和作业时间不确定性的泊位分配问题(Berth Allocation Problem, BAP)问题，以最小化等待时间和最小化与成本最低的泊位的偏差为目标，提出一个基于模拟退火的两阶段迭代算法对该问题进行了求解；Xu等[11]考虑了同样的问题，以最小化离开延迟和最大化时间缓冲为目标建立了数学模型，提出了基于模拟退火算法和分支定界法的鲁棒性泊位调度算法；Zhen[12]在考虑船舶作业时间不确定性的同时，还考虑了船舶周期性到达的BAP问题，提出一个随机规划模型和一个鲁棒性模型，并针对这两个模型分别提出了启发式算法对问题进行了求解；Liu 等[13]考虑船舶到港时间不确定和作业时间不确定，以最小化延期成本和最小化非最优泊位成本的加权和为目标，建立了一个混合整数及两阶段随机规划模型，在此基础上，提出了自适应差分进化(Adaptive Differential Evolution, ADE)算法并与成本导向(cost oriented)及鲁棒性导向(robust oriented)的调度进行了对比，证明了算法得出的调度的有效性。

总之，由于集装箱码头问题的综合性，许多研究开始考虑泊位、堆场等的联合调度问题。同时，在此基础上，由于船舶到港的周期性，在考虑联合调度问题的同时，还涉及了模板计划问题。而伴随着模板计划问题同时出现的还有不确定性问题，尽管已经有学者讨论了不确定环境下的泊位分配问题，也考虑了模板计划问题，但将泊位和堆场同时放在不确定环境下一起进行讨论的则几乎没有，而值得一提的是，Moorthy 等[7]同时考虑了这些因素，然而其问题的背景为中转港，未考虑进出港所关心的堆场容量等问题。基于以上原因，本文在进出口港的背景下，考虑集装箱码头的泊位与堆场调度问题，并着眼于对船舶到达时间不确定性和周期性到达进行研究。

1 泊位—堆场资源集成调度问题模型

基于码头的实际情况，现作出如下假设：①连续型泊位，并离散化处理，即船舶可停靠在岸线任意处；②船舶为动态到达，即船舶依次到达，需遵守船舶不早于预计到达时间的约束；③出口箱预留时间与进口箱留存时间相同，且前者只与船舶预计到达时间有关，即进口箱提前从闸口端进入堆场等待装运的时间和出口箱从船舶卸载至堆场后等待闸口端运走的时间相等，且前者按预定时间到达堆场后不再随船舶实际到达时间的延后而延迟；④集装箱对堆场资源的占用采用保守策略，即船舶进口箱从提前期时刻起即保持对堆场资源最大的占用(与该船进口箱数量一致)，至该船舶离港时刻才统一进行释放，出口箱亦然；⑤考虑全堆场，即满足不超过堆场的最大容量限制的约束，因中转港中集装箱的搬运绝大部分集中在堆场与海侧区域，而进出口港的搬运任务中仅一半在此，另一半则在堆场与陆侧区域，故比起前者由于集中搬运所导致的搬运距离成本高、交通拥堵等问题，进出口港更在意的是为满足陆侧闸口端搬运需求所应考虑的堆场能力问题，即堆场容量限制；⑥考虑船舶到达时间不确定性；⑦船舶以周为单位周期性到港。

基于以上假设，泊位与堆场两类资源的约束与关系表示如图1所示。图中上下部分分别表示泊位和堆场计划。矩形框表示船舶对泊位的占用及进出口箱预留时间，分别对应各时间段内集装箱对堆场的占用情况。此外浅灰色的矩形框表示船舶开始作业时间的延迟，用以应对不确定性。在决策计划过程中，应满足各船舶的泊位计划不冲突及船舶装卸载箱的总量不超过堆场容量的约束。

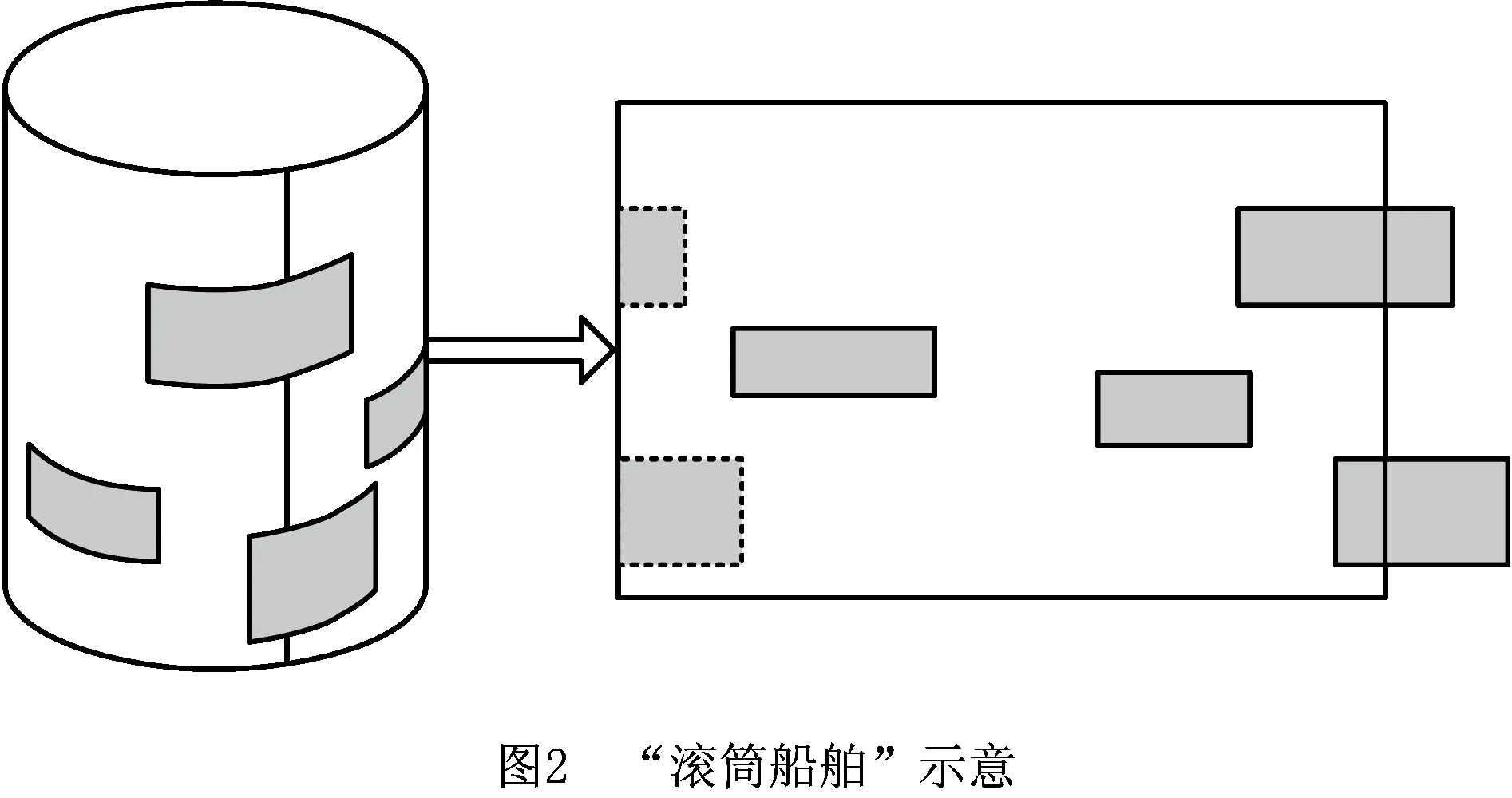
为决策周期性到达船舶的泊位计划，本文参照Moorthy 等[7]的滚筒式添加泊位的方法来表示周期性船舶，以下称“滚筒船舶”。如图1虚线矩形所示，将那些跨越了周期边界的进入本周期内的上一周期船舶和进入下一周期的原本属于本周期的该船舶看作是同一艘船舶，即“滚筒船舶”。这就如图2所示，将一张代表一个决策周期的矩形白纸卷成一个圆筒，上面的贴纸代表船舶，接合处的贴纸既可视作上一周期也可视为本周期的，即“滚筒船舶”，在圆筒上，就可以将它们视为同一艘船舶。如果“滚筒船舶”在一个决策周期内的计划可行，意味着该决策在其他周期同样有效，因此只需为所有船舶在一个周期内找到一个可行的计划即可。

由此，针对所界定的问题边界，建立周期性及不确定性环境下，集装箱码头泊位—堆场资源集成调度问题模型。

(1)符号说明

i表示船舶编号；j表示离散化处理的泊位编号；t表示离散化的时间编号；k表示周期编号。

(2)输入参数

(3)决策变量(基础计划，X0)

(4)决策变量(不确定性场景ω下第k周期的实际执行，XR(ω,k))

目标函数：

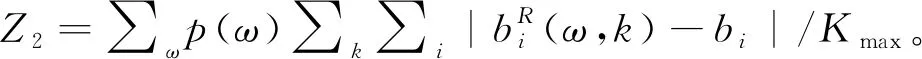
(1)

s.t.si≤t·xit+M·(1-xit),

∀i∈V,t∈To;

(2)

ei≥t·xit,∀i∈V,t∈To;

(3)

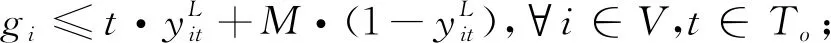
(4)

(5)

(6)

(7)

(8)

(9)

ei=si+Mi-1,∀i∈V;

(10)

∑t∈Toxit=ei-si+1,∀i∈V;

(11)

(12)

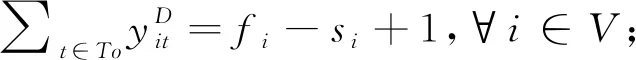
(13)

bi≤j·wij+M·(1-wij),∀i∈V,j∈J;

(14)

bi+Li-1≥j·wij,∀i∈V,j∈J;

(15)

∑j∈Jwij=Li,∀i∈V;

(16)

(xit+wij-1)/2≤αijt≤(xit+wij)/2,

∀i∈V,j∈J,t∈To。

(17)

(18)

∀i∈V,t∈To；

(19)

(20)

∀i∈V,t∈To；

(21)

∑i∈Vαijt+∑i∈Vαij(t+T)≤1，

∀j∈J,t∈T1；

(22)

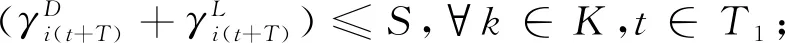
(23)

si∈{Ai,…,2*T},ei∈{Ai,…,2*T}，

∀i∈V；

(24)

∀i∈V；

(25)

bi∈{1,…,J-Li+1}，∀i∈V；

(26)

∀i∈V,j∈J,t∈To；

(27)

XR(ω,k)=Fω(X0)，∀ω∈Ω,k∈K。

(28)

目标函数为优化不确定性条件下的质量鲁棒性及解鲁棒性，前者以船舶总等待时间的期望衡量，这是通常采用的目标，后者以靠泊位置相对基础计划变动的期望衡量，用以衡量因靠泊位置的变动而发生的额外临时搬运与调度等成本，以及对计划稳定性所造成的损害成本。注意这里的临时搬运成本不同于中转港中的船与船之间的搬运距离成本，后者属于计划中的成本，而前者是计划外的由于不确定性而产生的成本。两者均定义在所有的待评估周期上，以体现周期性考量。

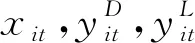
对于反应式调整过程，其核心表达式为(28)，该式代表了从确定性环境下的基础调度计划X0到不确定性场景ω下第k周期的实际执行结果XR(ω,k)的映射关系Fω。这是考虑到不同的反应策略下映射关系各有不同，且通常不存在显式表述。其具体过程将在反应式调度算法中详述。另外，调整决策变量是基础计划的实际执行结果，因此也必须服从后者的定义域和内在约束关系，这里不再一一列出。

2 算法设计

由于目标函数为双目标且需要仿真获得，无法通过模型的线性化求解直接得到，因此，在满足以上模型约束的前提下，本文提出如图3所示的前摄—反应调度算法框架。其中，前摄计划通过自适应遗传算法及启发式算法规则得到，反应阶段则使用特定的反应规则进行仿真以获得两个目标函数并验证前摄计划的有效性。本文将该算法定义为ASB。

2.1 基于代理目标的前摄计划算法设计

前摄计划由搜索与评价两部分组成，其中搜索部分使用了遗传算法进行搜索，为改善遗传算法早熟收敛以及收敛性能差的缺点，使用了自适应的策略进行改善[14-15]。由于自适应遗传算法已标准化，故不再赘述，这里仅介绍编码、初始化和早熟机制等不一样的地方。

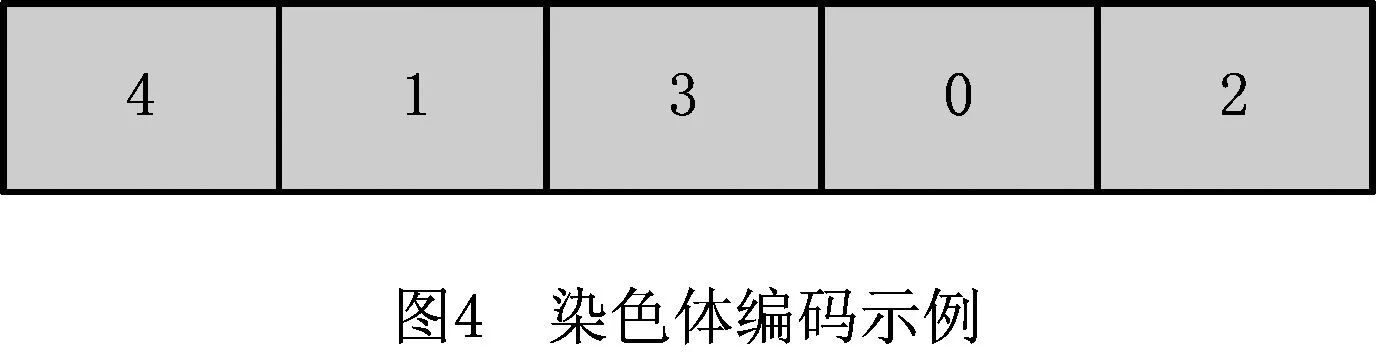
在编码方面，采用自然数编码的形式。如图4所示，编码为一条长度为Vmax的优先级序列ch=(I1，I2，…，IVmax)，即染色体。数字表示船舶的编号，位置表示船舶的优先级。

在初始化方面，为提高搜索效率，本文根据先到先服务(First Come First Served，FCFS)规则、最短处理时间(Shortest Processing Time，SPT)和最长处理时间(Longest Processing Time，LPT)规则等常用规则生成部分染色体，其余染色体均随机生成。

此外，为防止早熟，算法引入了重启机制，当目标函数连续δ代(文中设为15)未发生改善时，启用重调度机制，将群体一部分(文中设为20%)最好个体直接复制到下一代，另一部分(文中设为30%)用随机法重新生成，其余个体以较大概率(Pm=0.9)发生变异。

在评价环节，包括启发式算法规则解码与目标函数评价两部分，其中解码过程的伪代码如下所示。这里blockoccupiedt和berthoccupiedtb分别表示堆场在t时刻的占用量和泊位b在t时刻的占用情况，另外，在决策前摄计划中，为了表示“滚筒船舶”，本文对于blockoccupiedt和berthoccupiedtb中t<0的部分，令t=t+T；对于t>T的部分，令t=t-T。

Begin

遍历优先级列表pl，令i←pl1to plVmax

令si=Ai，如果船i未安排完毕，则si++

则令bi=0，如果船i未安排完毕且bi≤Jmax-Li，则bi++

如果对于∀t∈{si,ei}，满足对于∀b∈{bi,bi+Li}，berthoccupiedtb=0

则船i安排完毕

则更新堆场泊位占用情况

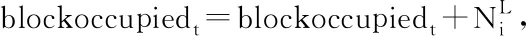
End

解码完成后，将得到的解代入目标函数进行评价。在实际求解过程中，由于原目标函数需通过抽样仿真才能得到，且为多目标优化，为加快搜索速度，本文首次提出如下代理目标函数：

minZ=∑i(ei-Mi-Ai)-λ∑isti。

解的鲁棒性参考了文献[16]中的松弛时间(slack time)的概念，使用了sti来代理，松弛时间指泊位占用有重叠的一前一后两艘船舶中，前一船舶离港后至后一船舶靠泊时的这段时间，“松弛”是指如前船出现延迟，只要延迟量在这松弛时间以内，则不会对后船造成影响。通过加权和形式构造单一目标，既加快了算法效率，又同时考虑了两个鲁棒性指标。这里的sti定义为：sti=sigmoid(sp1-ei)+sigmoid(sp2-ei)，其中p1∈Pi,p2∈Pi.p1和p2分别表示船舶i的所有紧后船舶中最早开始的船舶和除p1外最早开始的船舶。其具体意义如图5所示。以船舶0为例，紧后船舶是指与其在泊位上存在冲突的所有在其后到达的4、5、6船舶。根据它们的到达时间，船舶4即为p1，船舶5为p2。sp1-ei表示船舶p1的开始作业时间减去船舶i的完成作业时间，sp2-ei同理，它们的加权和衡量了船舶i与其紧后船舶的松弛时间。为兼顾两个鲁棒性，本文希望船舶的松弛时间能在一个最适范围内，当松弛时间较小时能尽快增大，而松弛时间很大时又不让其再继续增加而影响其他船舶，因此使用Sigmoid函数对其进行加权。

这里sti只考虑了紧后船舶中最早开始的两条船，出于两方面原因的考虑：①由于在实际情况中，各类船舶的体积大小差别不会很大，故各船舶通常只会直接影响到最多两个紧后船舶的靠泊。如图5所示，船舶0最早开始的两个紧后船舶4和5之间，通常是无法再多容下一艘船停靠的；②由于对于像船舶6这样的船舶，通常不会直接受到船舶0的影响，即使真的因为船舶0导致船舶4和船舶5延迟进而导致船舶6延迟，关于船舶6的松弛时间计算也已在船舶4和船舶5中考虑到，因此不再加入船舶0的计算中考虑。

2.2 基于松弛时间的反应规则设计

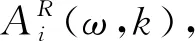
在ω中，由于船舶的实际到达时间会与计划产生偏差，因此还需要一套与前摄计划相匹配的调度规则以得出实际调度解。基于此，本文设计了如下的反应策略，即模型中的Fω部分。

本文通过调整泊位以使船舶更早开始作业，同时为充分利用船舶之间的松弛时间，防止船舶过度调整泊位打乱基础计划，本文设计了基于松弛时间的局部调整策略。该策略的核心思想如图6所示，首先根据前摄计划调度实际到达船舶；当资源不够时，将船舶靠泊时间及相应的堆场占用时间延后；若延后量超过st*，启用重调度，为船舶寻找临近可行泊位；若超过了泊位调整上限τ，或称阈值τ，则将时间后延，直到找到可用泊位为止。这样既能保证船舶尽快开始作业，又能充分利用基础计划中的松弛时间，防止重调度过于频繁，导致完全打乱前摄计划及很差的调度解的鲁棒性。

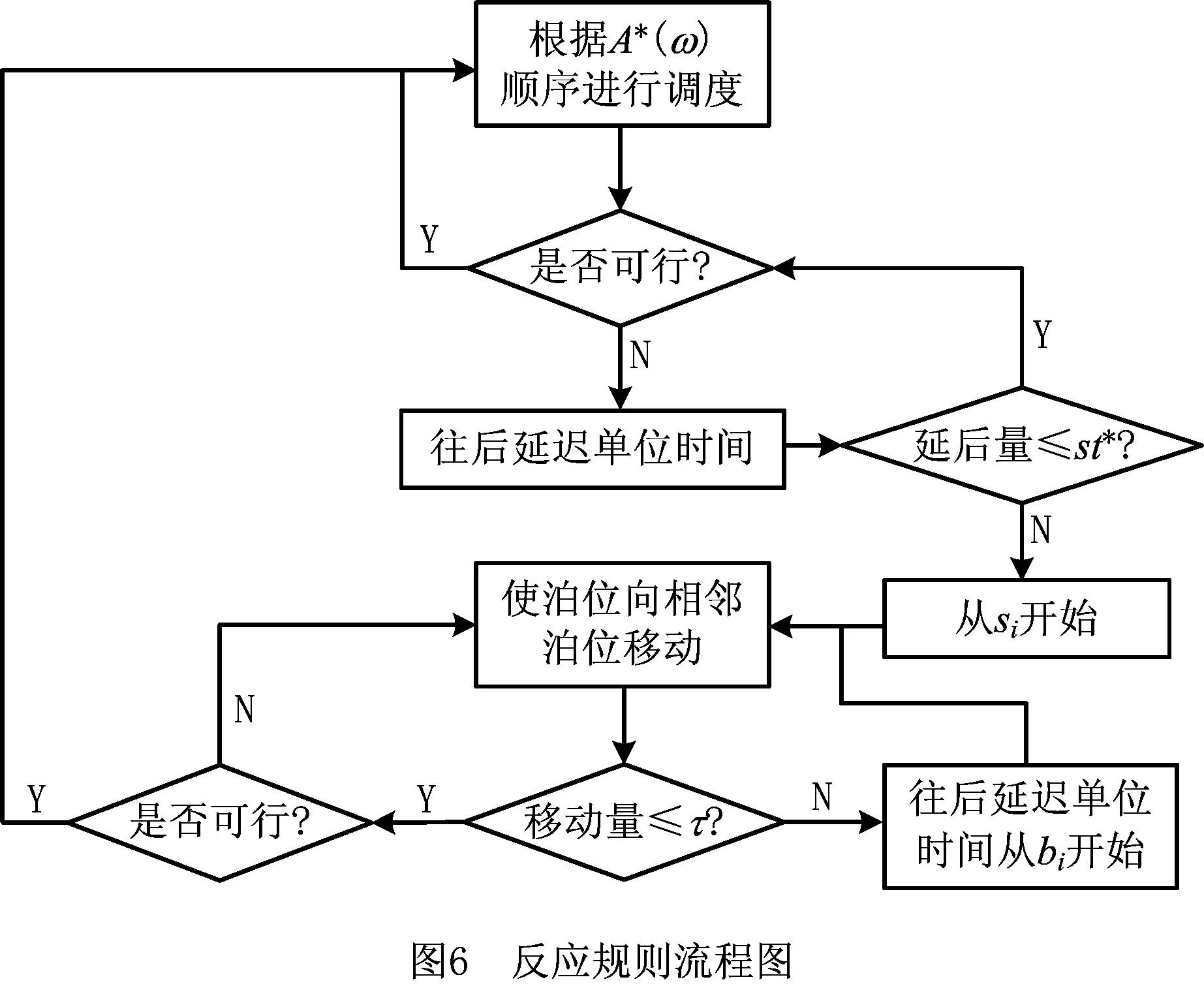
图6中的st*并不等于目标函数中的sti。考虑到sti只是对紧前紧后船舶之间松弛时间的一个参考指标，还需要在实验中确认st*取多少才能够得到较好的鲁棒性。

此外，由于本文假设为全堆场，未考虑集装箱在泊位与堆场间搬运的距离成本，该策略则可以给决策者提供一个参考：通过调整τ的大小，可以得到一系列不同解的鲁棒性与质量鲁棒性的调度方案，决策者可根据船舶的延迟时间成本和运输成本进行权衡，以得到一个最优方案。

注意这里调整泊位的方法，即用一部分解的鲁棒性换取质量鲁棒性，一方面意味着临时成本提高而船舶的延期成本降低，另一方面由于进出口港中堆场的集装箱状态将被作为陆侧闸口端的输入进行决策，而船舶能尽量按照计划进行作业，也意味着堆场集装箱的资源状态更加稳定，一定程度上增加了堆场资源解的鲁棒性，只是为目标函数相对简洁，本文不再加以考虑。

3 数值实验

3.1 实验对照

为验证算法的有效性，本文设计了对照组，定义为ATB。对照组同样采用本文提出的算法框架，并参考BAP的传统做法，在目标函数上，采用了如Xu等[17]、Imai等[18]使用的最小化在港时间的目标，本文中其定义如下：

minZ=∑i(ei-Mi-Ai)。

在调整策略上，使用了如文献[19]里所阐述的常见的右移策略(Right-Shift Policy)，即在资源不够时，泊位不变，将时间延后直到资源足够为止。

3.2 实验基本参数设置

为验证本文提出的模型、算法和反应策略的有效性，参照Meisel 等[20]和Zhen等[4]的参数与计算方法，分别在小、中、大3种规模的情景下进行了数值实验，具体数值考虑泊位与堆场的利用率大致分别为50%和60%计算得出，即每种规模下每周船舶数为20、30、40；泊位数为70、100、140；堆场容量为900、1 300、1 800。堆场容量的单位设为岸桥·时，在实际情景中，可根据码头的岸桥工作效率将该单位换算成集装箱数量。在反应阶段，模拟了半年的到达时间服从N(Ai,(10/3)2)的船舶序列进行仿真。为排除偶然误差，每种规模的集装箱码头情景各进行了10组不同的算例测试，每组算例中，分别生成大、中、小3种规格的船舶，三者各占1/3，具体数值参照文献[4]，其中岸桥数取用平均值。此外，本文将不同规模下的遗传算法参数设为同一组固定值。具体参数为：种群数量100，算法进化代数100，交叉和变异的相关参数Pc1，Pc2，Pm1，Pm2分别为0.7，0.3，0.3，0.2。在仿真阶段，抽样次数设为200次。

实验使用C#(Visual Studio 2015)进行编程以实现算法，测试平台为Intel Xeon E5-1650 v3处理器，3.5 GHz主频，16 G内存。下面介绍实验结果。

3.3 实验结果对比

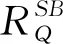
表1 20船规模下ASB与ATB对比

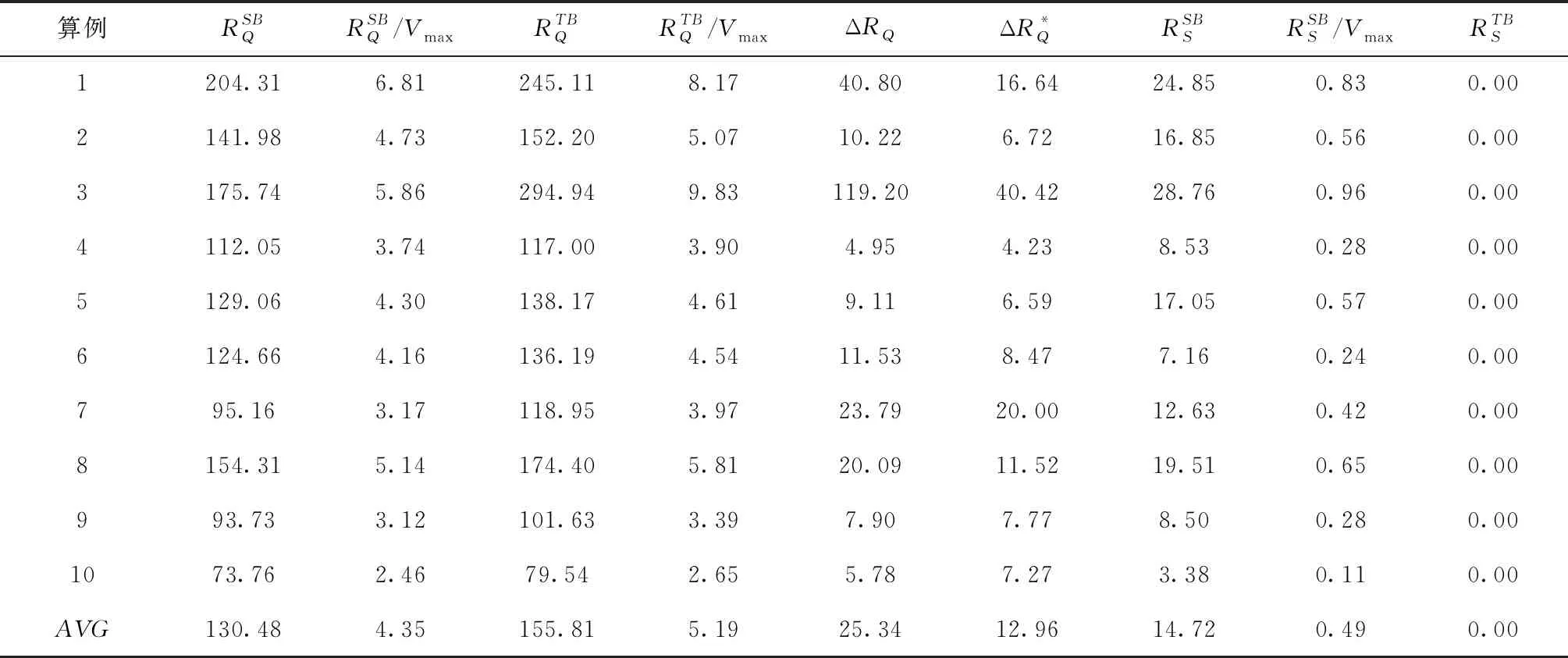
表2 30船规模下ASB与ATB对比

表3 40船规模下ASB与ATB对比

续表3

本文提出的ASB与ATB相比，质量鲁棒性都有了较大改善，在3个规模下，平均的改善比例分别达到了17.66%、12.96%和15.17%;另一方面，解的鲁棒性都保持在非常低的水平，每个规模平均每个船舶变动的泊位量只有0.73、0.49和0.08。因此，本文提出的算法对于改善集装箱码头泊位堆场周期性调度问题具有现实意义。

3.4 敏感性实验分析

图7是3个规模下两个鲁棒性与堆场容量取值(单位：岸桥·时)的关系。由图可以看出堆场容量对进出口港的运转效率也起着较为重要的作用。当堆场资源不足时，会导致船舶在港时间变长，即质量鲁棒性增加，这意味着船舶在入港时不仅需考虑其泊位是否被其他船舶占用，同样还需等待堆场资源足够方可进行作业。而值得注意的是，解的鲁棒性并没有随着堆场容量的减少而表现出相关的趋势，这是因为一旦堆场资源不足，只是调整泊位是同样无法满足约束的，两个资源的约束相对独立。

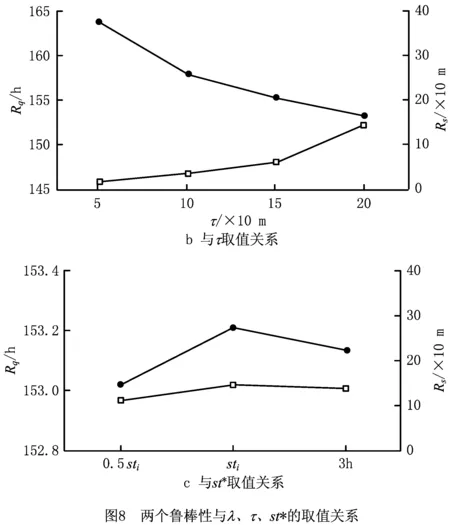
图8是20船规模下10个算例的平均质量鲁棒性和平均解的鲁棒性随三个参数分别取不同值下的表现。图8a显示两个鲁棒性与λ的取值未表现出明显相关性，表明代理目标只是对两个鲁棒性在一定程度上的反映。图8b表明随着τ取值的增大，质量鲁棒性随之减小，解的鲁棒性随之增大，这是由于τ的增大导致船舶可调整范围也随之变大，更多的船能尽快完成作业，但同时导致船舶与基础计划产生更大偏差，增大了其解的鲁棒性，在实际码头调度过程中，需根据对两个鲁棒性的要求来权衡τ值的大小。图8c表明不同st*的取值下两个鲁棒性表现各有不同，可视实际情况进行选择。

总的来说，本文提出的ASB与传统的做法ATB相比，在保证好的解的鲁棒性情况下，对质量鲁棒性的改善有着较大的现实意义，且为两个鲁棒性在实践中的权衡提供了一定的参数修改方向。然而值得注意的是，个别算例改善比例并不突出，这是由于代理目标函数及调整策略与两个鲁棒性之间的复杂关系造成的，这也从侧面说明了该问题的难度极大，难以找到明确的优化方向。

4 结束语

本文以集装箱进出口港为背景，研究泊位分配、堆场分配、船舶到港周期性及不确定性等因素影响下的资源计划与调度问题。构建了相应的混合整数线性规划的数学模型，基于模型提出了前摄-反应调度的启发式求解算法，并提出了代理目标的方法来评价中间解的效果，在效率上大大优化了算法。同时还提出了基于松弛时间的启发式调整规则。在最后的实验结果上，与设置的对照组相比，本文算法的有效性也得到了验证。为提高集装箱码头服务水平和减少运营成本提供了可参考的思路。然而出于问题规模太大的考虑，本文将堆场设为了全堆场，并未考虑到集装箱在各个堆区的占用情况，此外，本文所考虑的不确定性主要来源于船舶到港时间的不确定性，未来将考虑作业时间的不确定性。