基于跳度约束的重叠拐角高速加工平滑算法
2020-04-08张立强郭景浩
王 勇,张立强,郭景浩
(上海工程技术大学 机械与汽车工程学院,上海 201620)
1 问题的描述
传统的数字控制(Computer Numerical Control, CNC)系统在对具有复杂轮廓的零件进行加工制造时,通常对几何路径进行离散化处理,采用基本的G01指令对路径插值[1]。但是这样的加工路径仅仅是位置连续的,在加工过程中,进给运动必须在路径拐角处减速至停止,否则,驱动器的加速度值或跃度值将有可能超出系统限制,导致加工零件表面的光滑度遭到破坏[2-4],形成具有明显进给标记的粗糙加工表面,导致加工时间延长。解决这一问题的常用方法是采用样条曲线进行插补,使机床能够在加工路径的拐角处实现连续不间断进给运动,常见的样条曲线有:PH(Pythagorean-hodograph),Bezier和非均匀无理B样条(Non-Uniform Rational B-Splines, NURBS)曲线等[5-8]。但这种思路通常仅考虑了加工路径拐角处的平滑转接,不足以应对实际加工中的特殊情况,如:在粗加工或者半精加工中,由于设置的轮廓误差较大,造成局部的拐角轮廓重叠现象,如图1所示。一旦出现这种情况,进给运动必须在拐角处降低转接速度,否则重叠部分的进给运动就会超出驱动系统的限制,引起机床进给颤动。但这种做法浪费了驱动器的运动性能,无法获得时间最优的进给运动,同时加速度轮廓也会存在跳动或不可导点,影响加工质量。
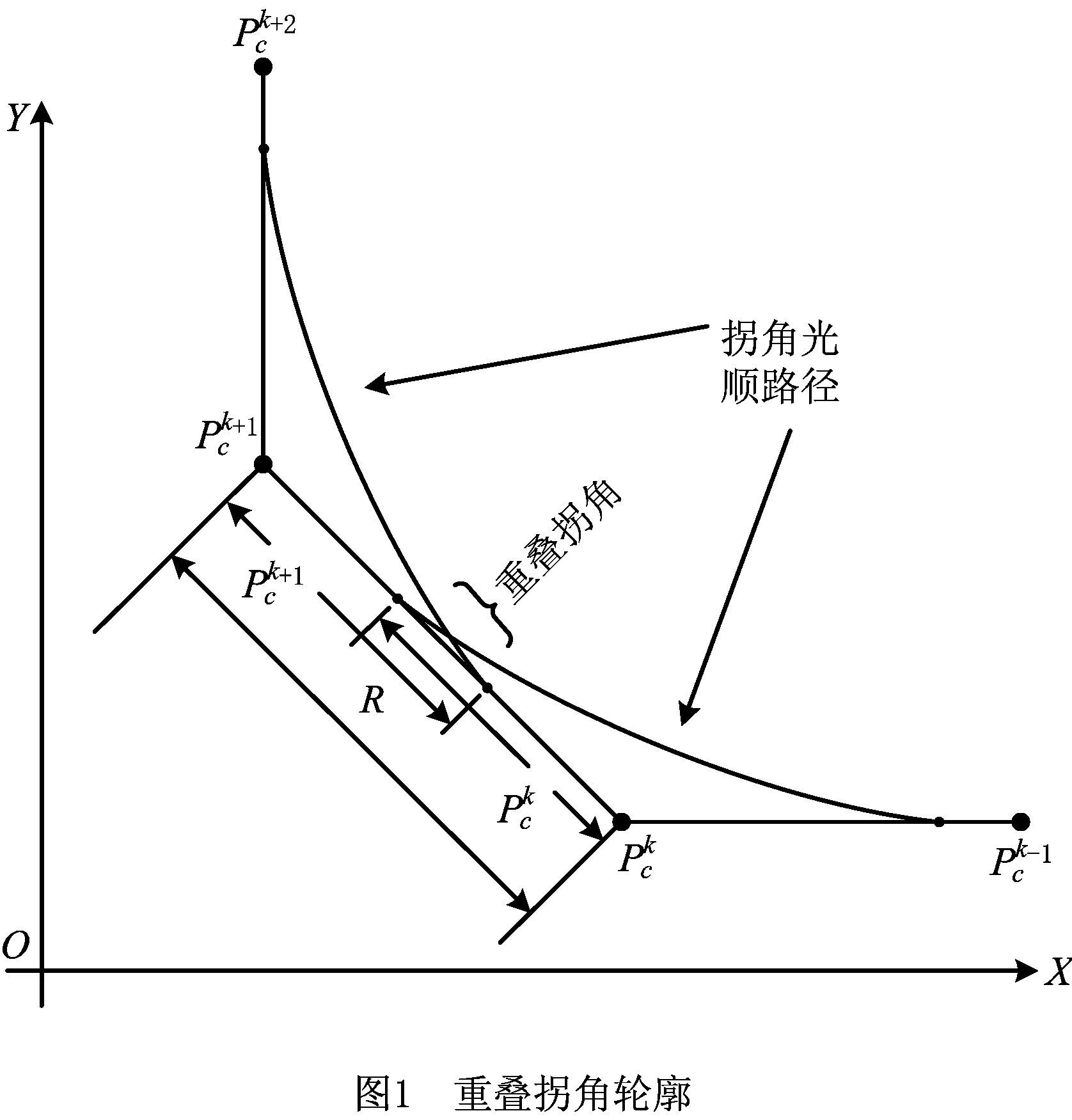
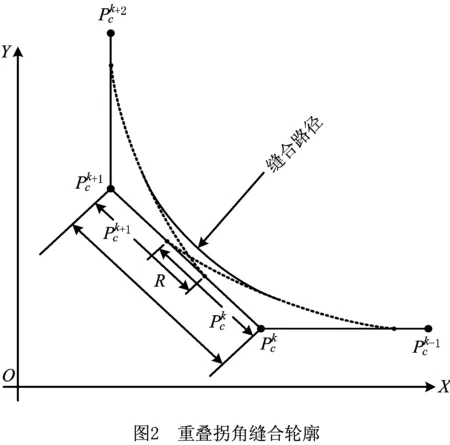
目前,国内外对上述这种特殊情况主要还是从样条曲线插补和运动学两部分来探究。样条曲线插补法首先用样条曲线插补前后两个重叠的拐角,生成多个控制点的样路径,再进行速度规划,使得进给运动可以平滑转接。但是这种两步规划的方式大大增加了数控系统的计算量,造成严重的计算负载。近年来,有学者从运动学角度进行研究,如Sencer等[9]提出了一步实现不间断进给运动技术,Tajima等[10]提出了基于跃度约束的拐角运动学平滑算法,实现进给轴在拐角处的最优运动。Zhang等[11]在Tajima基础上提出了基于跳度约束的加速度平滑算法。Tajima等[12]又提出通过平滑两个相互重叠拐角轮廓的中点,可实现在重叠拐角轮廓部分进给运动平滑转接。文献[12]中提出通过跃度限制加速度曲线,虽然平滑了重叠拐角部分的转接运动,但加速度曲线还存在严重的突变点和不可导点,在拐角轮廓的中点处加速度值会产生突变引起惯性振动,导致工件表面形成明显的进给标记。本文在文献[11]和文献[12]的基础上,通过连接重叠拐角的轮廓中点,以两个中点处的速度、加速度、跃度和驱动器运动性能为边界条件,提出基于跳度限制加速度的重叠拐角轮廓平滑算法,实现进给运动在重叠拐角轮廓处速度和加速度平滑转接。最后对所提算法进行实验分析,通过对比传统的点对点插补算法验证本文算法的有效性。
2 基于跳度约束的运动学平滑算法原理
为便于理解,下文中出现的各符号含义见表1中的符号说明。
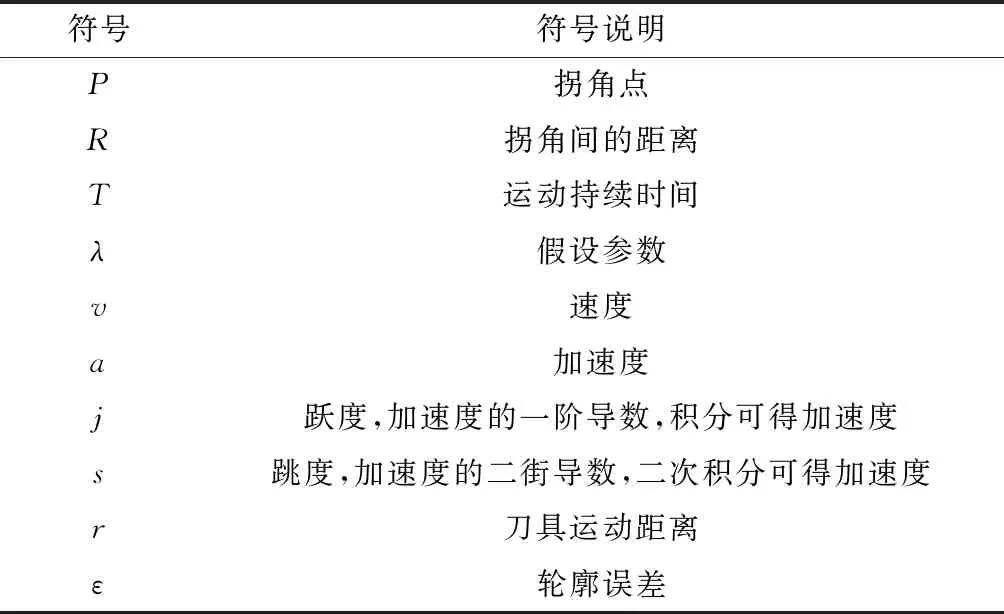
表1 符号术语表
2.1 二段平滑插补算法
本节针对重叠拐角轮廓现象提出基于2段跳度限制加速度曲线的平滑过渡算法,将转接运动过程分解为两部分来处理,假设Tm为整个过渡过程的总时间,设T1=λxTm为第一阶段持续时间,T2=(1-λx)Tm为第二阶段持续时间。通过对2段跳度限制加速度曲线再附加拐角中点处的边界条件,即可求得2段平滑过渡算法的各项所需参数。跳度约束曲线如图3所示。
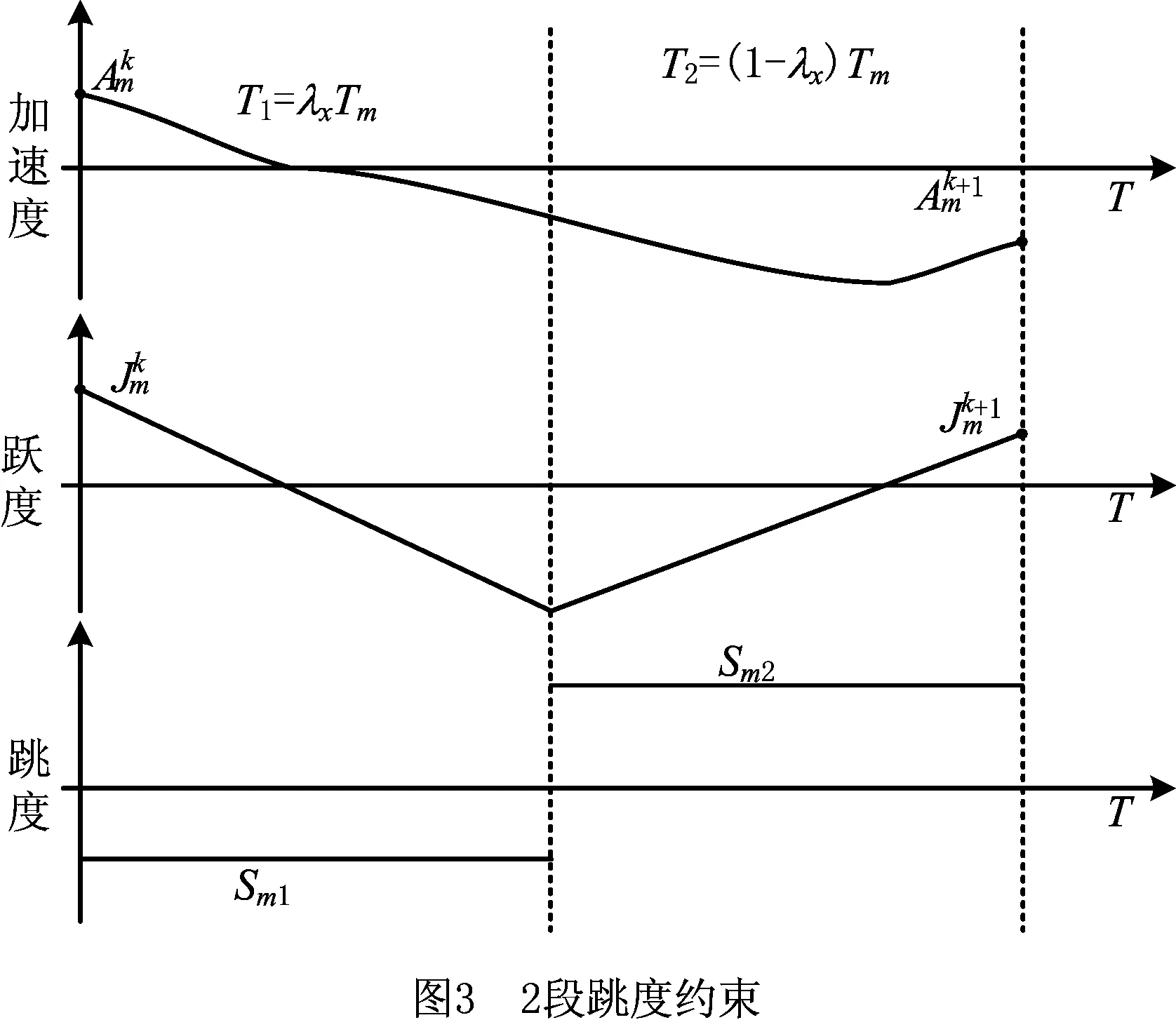
用S表示跳度,根据文献[11]所提的跳度约束加速度曲线公式,则第k个拐角轮廓中点处的跃度(j),加速度(a)和速度值(v)在X方向和Y方向可分别表示为:
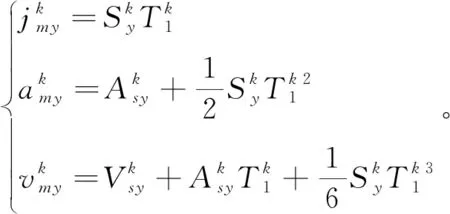
(1)
因此,基于跳度限制加速度曲线的2段平滑过渡算法的公式为:
jx(τ)=
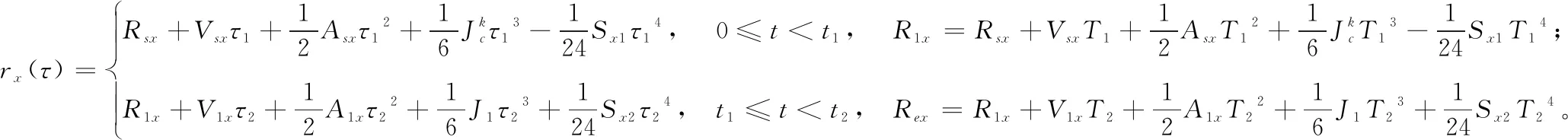
(2)
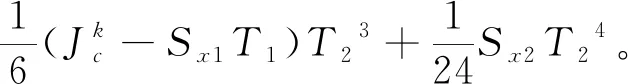
(3)
通过设置λx=0.5,使前后两段运动时间相等,即T1=T2,代入式(3)可以求得X轴2段平滑过渡算法的方程组:
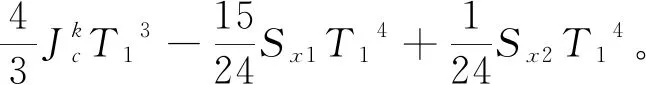
(4)
式(4)可化简为:
(5)
通过式(5)即可求出X轴的各项参数,Y轴的各项参数可以用类似求法。需要注意的是,求出的各项参数不能超出驱动器的运动极限:
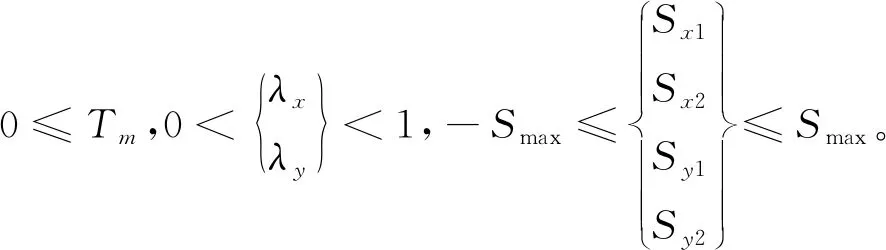
(6)
若所求得的参数值超出驱动器的运动极限,则通过极限值反求出拐角轮廓中点处的转接速度,从而推导出该拐角平滑算法所允许的最大转接速度,实现对超出驱动器运动极限部分的参数调整。
2.2 四段平滑插补算法
采用2.1节所述的二段算法,进给运动过程的加速度和速度曲线都能实现平滑转接,插补后的加工路径能够实现曲率光顺达到G3连续。但要能够充分发挥驱动器的性能,还需要进一步调整各项参数。当求出跳度S后,可根据式(7)反求出跳度J、加速度A和速度V:
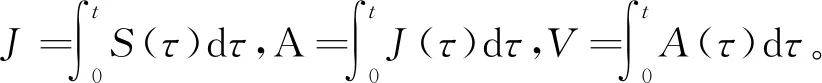
(7)
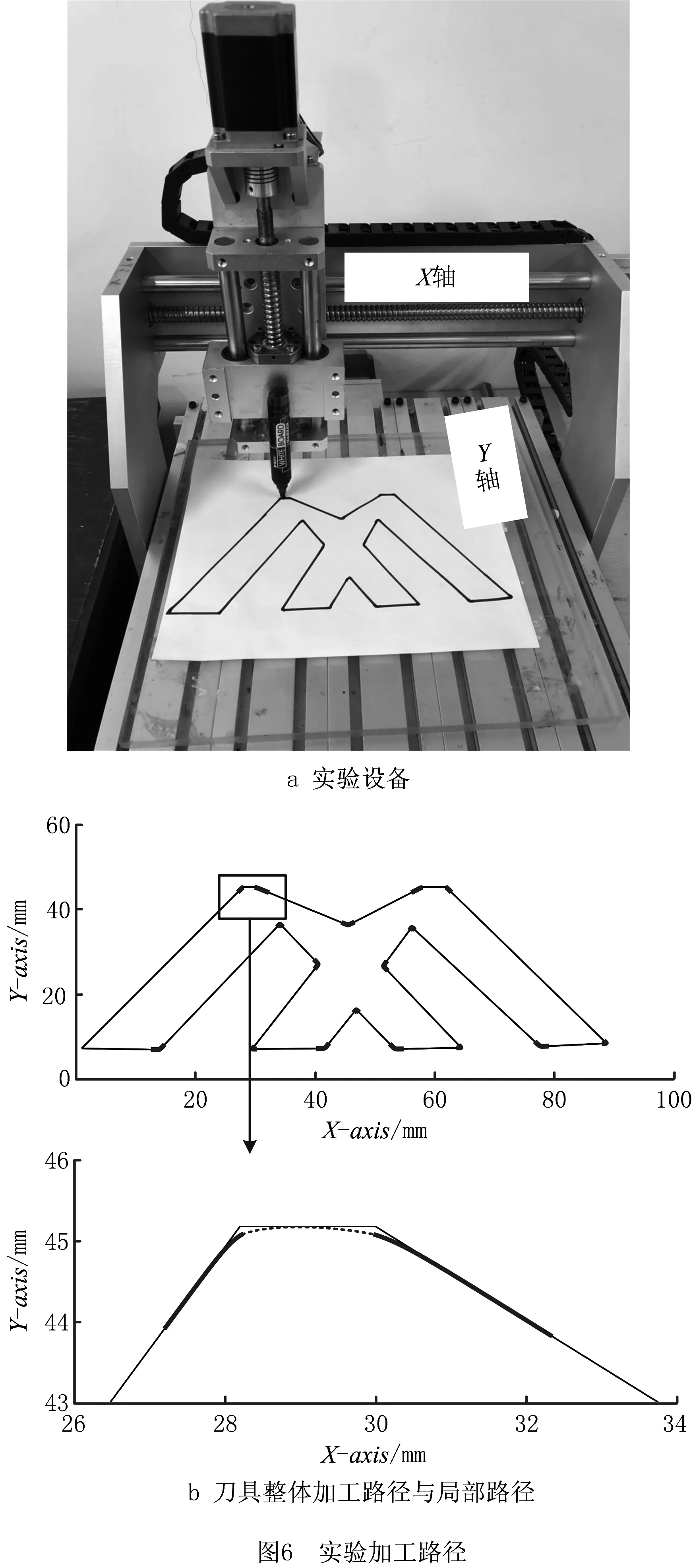
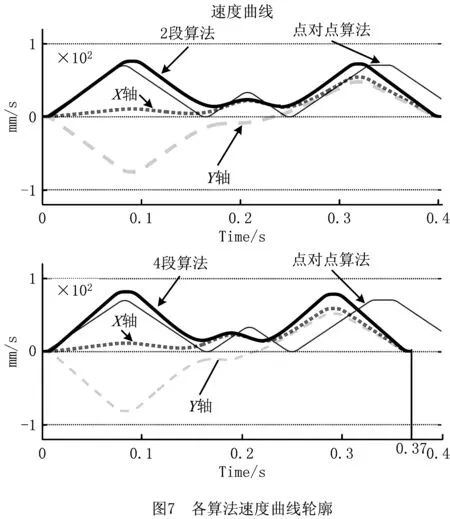
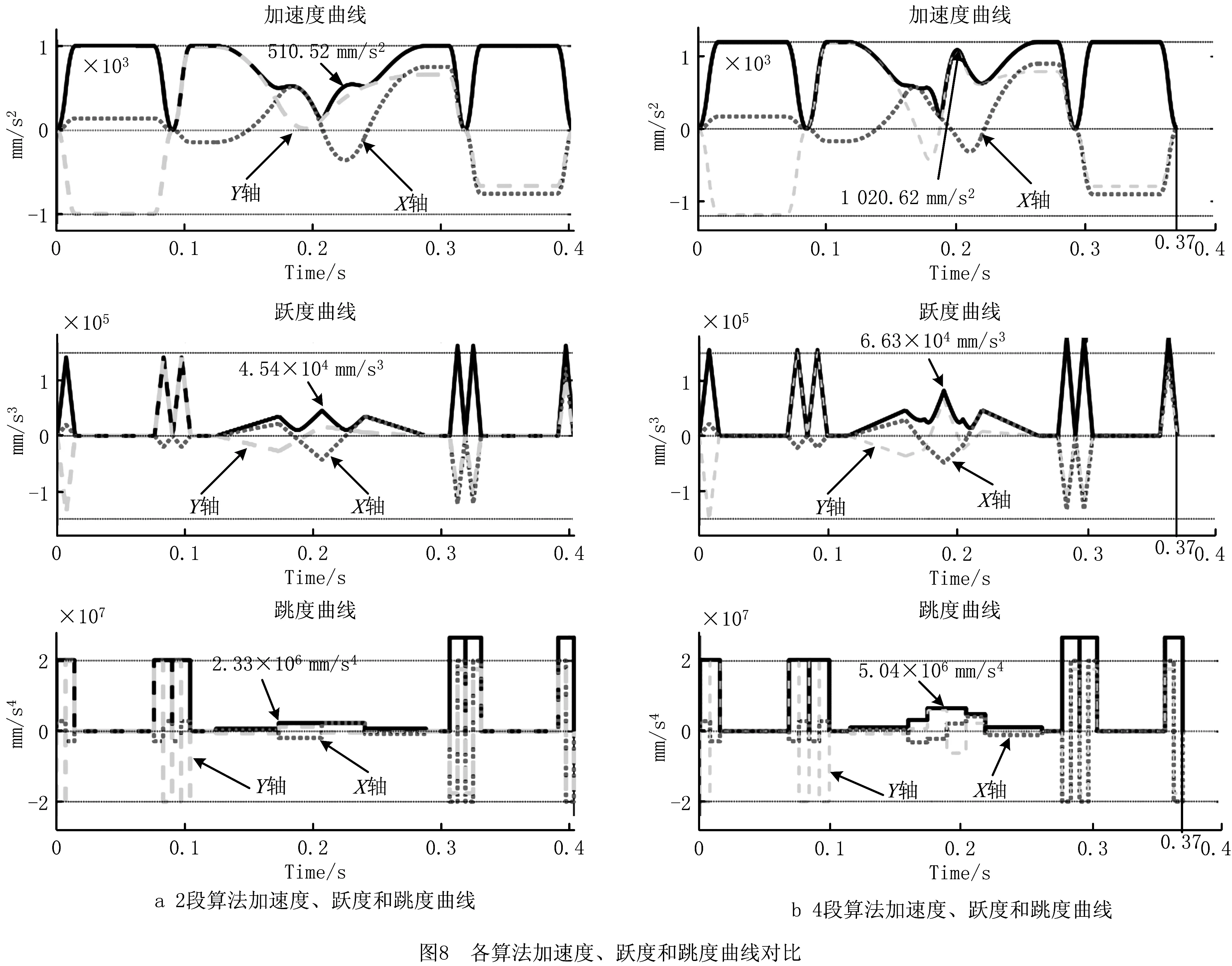
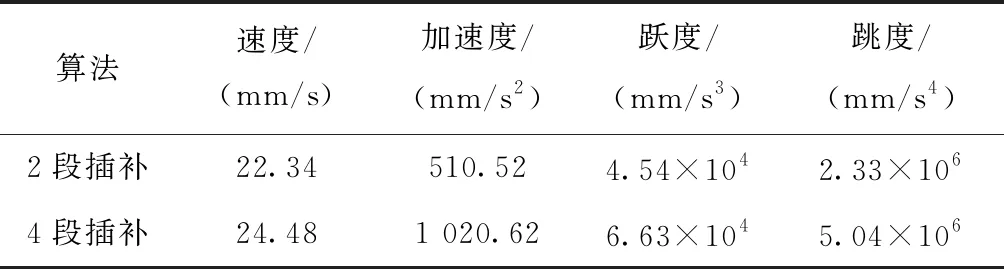
此时若满足S 基于跳度限制加速度曲线的4段平滑过渡算法的公式为: (8) 式(8)描述的过程即是:初始时刻刀具在前一拐角轮廓中点处在X方向上以4段给定的跳度值作为约束,运动至后一拐角轮廓中点处。其中Ji、Ai、Vi和Ri(i=1,2,3,4)分别为Ti时刻的跃度、加速度、速度和位移。前后两个拐角轮廓中点处的跃度,加速度,速度和位移值满足式(1),通过将其作为边界条件附加到4段平滑过渡算法,刀具在后一个轮廓中点处的运动状态可通过前一轮廓中点处的状态进行推导,如式(9)所示: (9) 其中:Tm是运动过程的总持续时间,Sm1~Sm4为各个阶段的跳度值,X轴、Y轴的边界条件共有11个未知量:Sm1x~Sm4x,Sm1y~Sm4y,λx,λy,Tm,却只有8个方程,因此需要增加边界条件才能求解。为方便求解,令λx=0.5,Sm2x=-Sm3x,Sm1x=-Sm4x,代入式(9),经化简整理后得到式(10)。由此可以求出Sm1x~Sm4x和Tm。根据所求得的Tm,使用相同的方法可以将Y轴的未知量求出。 (10) 此处同样需要注意的是,求出的各项参数不能超出驱动器的运动极限: (11) 若求出的值超出驱动器的运动极限,则可以通过极限值反求出拐角轮廓中点处的转接速度,从而推出该拐角平滑算法所允许的最大转接速度,实现对超出驱动器运动极限部分参数的调整。上述算法能够在实现速度和加速度的平滑转接,获得曲率光顺的加工路径的同时不浪费驱动器的性能。算法流程图如图5所示。 为验证所提算法的有效性,对连续短线段加工路径分别采用传统点对点插补算法和重叠拐角轮廓插补算法进行对比分析。 实验设备如图6a所示,X-Y数控系统由两个线性电动机驱动,为保持良好的位置同步和路径跟踪,伺服放大器设置为转矩(电流)控制模式下操作,线性编码器的反馈分辨率为0.8 um,伺服系统的闭环采样时间为0.1 ms,X轴与Y轴的位置反馈带宽为ωn=25 Hz。实验加工路径为如图6b所示的“倒双V”路径(图6a所示为便于示意进行放大后的实验路径),总长度339.49 mm,共有18个拐角,其中4个拐角形成2处重叠路径,方框图的局部路径为其中一处。局部拐角路径长度为8.92 mm,包含两个拐角,角度大小分别为125.43°和149.98°。在该段路径上分别进行点对点插补算法和重叠拐角轮廓插补算法对比实验。其中点对点插补算法要求刀具运动到每个拐角点前开始减速,直至拐角处完全停止,再进行转向进给,完全与G01代码所规定的路径同步;重叠拐角轮廓插补算法须设定最大允许轮廓误差为0.1 mm。利用伺服控制器对不同算法进行实时采样和命令。设置驱动器各轴的最大进给速度为100 mm/s,最大加速度为1 000 mm/s2,最大跃度为1×105mm/s4,最大跳度为2×107mm/s4。拐角中点缝合加工路径如图5局部路径放大所示。图7所示为各算法在局部路径上运动的速度曲线轮廓,可以看出点对点插补算法速度曲线存在较大的波动,且该算法需要在每一个拐角处完全停止,加速度跳动,对驱动器的负载较大。 3种算法对比如表2所示,在包含重叠拐角轮廓的局部路径中,2段插补算法与4段插补算法的加速度曲线都达到G1连续,在加工时间方面分别比传统点对点插补算法减少了15.4%和22.2%。4段插补算法与2段插补算法相比,加工时间减少了8.1%。图7和图8显示了在上述驱动器设定参数下,运用2段算法与4段算法在局部路径中的速度曲线、加速度曲线、跃度曲线和跳度曲线。两种算法的速度曲线波动都较小,趋于平稳,能够一直以较大的速度进给,并且加速度曲线达到G1连续。图7和图8中的数据整理如表3所示,可以看出,在局部路径中采用2段插补算法时,在经过重叠拐角轮廓处最大速度为22.34 mm/s,最大加速度为510.52 mm/s2,最大跃度为4.54×104mm/s3,最大跳度为2.33×106mm/s4,采用4段插补算法时各项运动参数都有所提升,分别为24.48 mm/s,1 020.62 mm/s2,6.63×104mm/s3,5.04×106mm/s4,因此采用4段算法可以更好地发挥驱动器的运动性能。 表2 算法对比 表3 2段算法4段算法运动参数 本文针对加工路径中的特殊情况即重叠拐角轮廓现象提出平滑算法,采用基于跳度约束加速度曲线的方式,保证加工路径在拐角处满足曲率光顺,实现平滑的速度和加速度转接。 本文所提算法中的参数计算没有高阶项,不需要进行深层迭代寻找最优解,满足数控系统插补算法实时性的需求。其中2段平滑插补算法已满足平滑地插补加工路径的要求,无需进给运动减少拐角转接速度或最大轮廓误差,即可实现平滑的速度和加速度转接;在其基础上使用4段平滑插补算法可以充分利用驱动系统的运动性能,获得时间最优的进给运动,但是相对于2段算法计算量较大,计算所得参数容易超出驱动器极限。 最后通过实验对比,两种重叠拐角轮廓插补算法的加工时间相比于点对点插补算法都减少10%以上。在实际加工中,较长的连续短线段路径往往包含数百甚至数千拐角,其中可能存在大量重叠拐角,因此使用重叠拐角轮廓平滑算法在复杂零件的生产和加工中能够显著减少加工时间,提高加工效率。本文的研究与实验都是在X-Y坐标系下进行的,为进一步应用于复杂零件的生产制造,可扩展研究到多轴加工领域。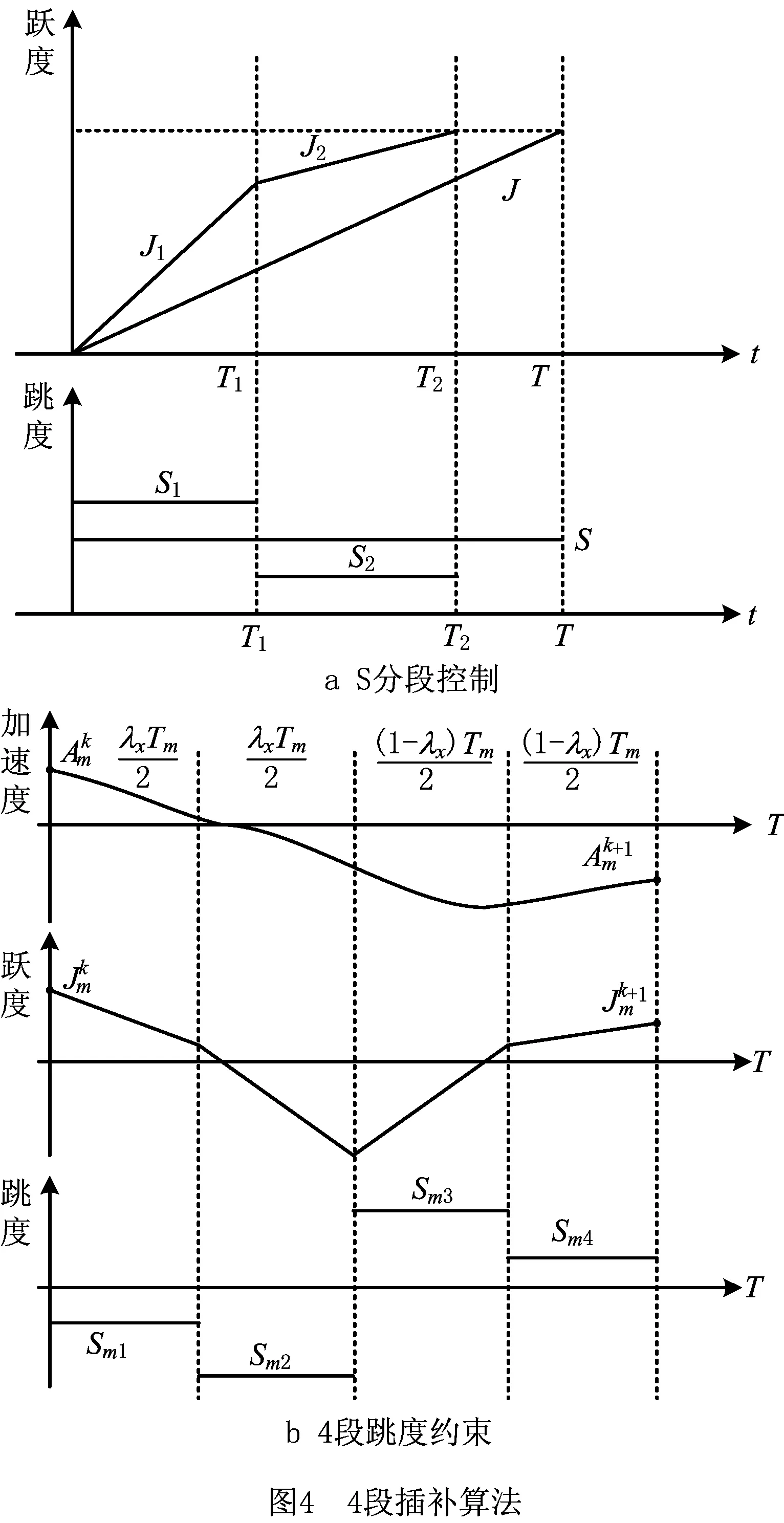
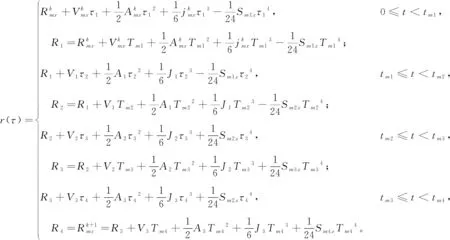
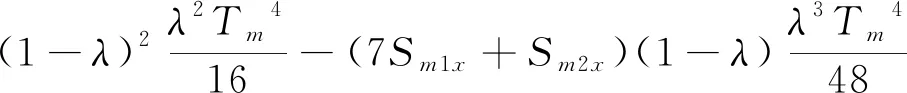
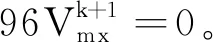
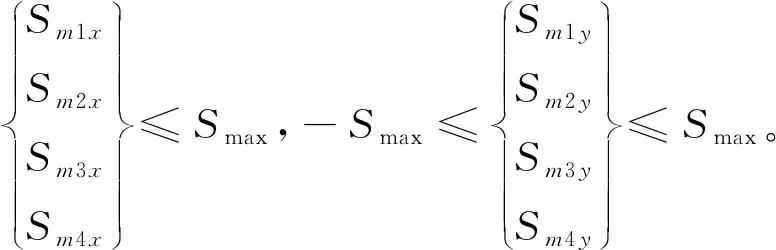

3 仿真分析

4 结束语
