基于差分进化算法的辅助燃油系统燃油转输参数优化

龚 昊

(中国商用飞机有限责任公司上海飞机设计研究院，上海 201210)

飞得更高、更快、更远一直是航空领域追求的目标。在飞机的气动外形和动力装置不进行改进的情况下，通常需要增加飞机的载油量才能实现飞机航程的增加或留空时间的延长。对于民用飞机而言，在改进原机油箱以增加载油量以外，更为便利的方式是在飞机机身货舱内安装辅助油箱，以存储更多的燃油[1]。通过辅助燃油系统将辅助油箱中的燃油转输至飞机的基本油箱中，供发动机消耗。国外采用这种方式的机型包括B737、B777、A319、ERJ190、世袭1000等。中国在民机加装辅助油箱方面的研究很少，目前尚无加装辅助油箱的国产民用飞机交付使用。

Fasanella等针对B737机身下部设辅助油箱的情况，建立了全尺寸三维有限元模型，并利用非线性瞬态动力学软件进行了坠落撞击仿真[2]。Gavel等针对带有辅助油箱的飞机，基于飞机级顶层需求，对燃油转输系统进行了概念设计[3]。刘胜君对加装了辅助油箱的BBJ公务机和ACJ公务机的特点进行了介绍[4]。刘德刚等对辅助油箱的设计、布置和安装进行了介绍，对采用增压气体转输燃油的辅助燃油系统的设计特点进行了分析[1]。

在辅助燃油系统设计中，燃油转输相关参数的确定是方案设计的核心，凭借工程经验人为给定的方式难于获得最优方案，可以考虑使用优化算法对设计方案进行优化。

随着人们对各种优化问题的关注，目前发展了诸多各具特点的优化算法，如遗传算法、粒子群算法等。其中，差分进化算法由Storn和Price于1997年正式提出，是一种基于种群的启发式进化算法[5]。差分进化算法以其算法结构易执行、优化效率高、参数设置简单、优化结果稳健等优点，受到诸多研究者的关注。Das等综述了差分进化算法的研究现状，并从基本概念、算法构造、控制参数、变量范围、优化目标等方面对差分进化算法进行了理论分析[6]。丁青锋等概述了差分进化算法的研究概况以及存在的问题，综述了差分进化算法在控制参数、差分策略、种群结构以及与其他最优化算法混合等4个方面的改进策略，并讨论了各自的优缺点[7]。

为了对燃油转输参数方案进行优化，本文将辅助燃油系统燃油转输设计过程抽象成约束优化问题，并对差分进化算法进行改进，在此基础上进行燃油转输参数的优化。通过本文的研究，完成了对辅助燃油系统燃油转输优化设计问题的求解，同时也为差分进化算法的应用研究提供了新的参考。

1 辅助燃油系统燃油转输工作原理

图1为本文所研究的辅助燃油系统进行燃油转输的示意图，辅助油箱采用闭式通气系统，利用飞机客舱的增压空气或发动机引气作为压力源，将辅助油箱中的燃油转输至原机的基本油箱。燃油转输过程的本质是用同体积的增压空气替代从辅助油箱转输出的燃油，这是当前民用飞机辅助油箱采用的主流方式[1]。

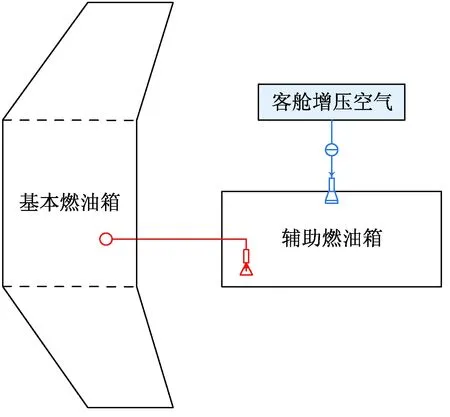
图1 辅助燃油系统燃油转输示意图Fig.1 Schematic diagram for fuel transfer of the auxiliary fuel system

理论上，燃油从辅助油箱向基本油箱的转输可能发生在整个飞行任务的任意飞行阶段。对于民用飞机而言，飞行时间最长的是巡航阶段，也是燃油转输最主要的阶段。因此，为简化问题，假设燃油转输仅在巡航阶段进行。

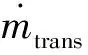
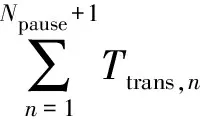
2 燃油转输优化设计问题

通常，满足要求的燃油转输参数方案不止一个，可以将其作为约束优化问题进行求解：

(1)

式(1)中：f(X)为目标函数：X=(x1,x2,…,xn)是优化变量；XU和XL分别为优化变量的上下限；hi(X)为等式约束；gj(X)为不等式约束。

辅助燃油系统燃油转输参数优化设计问题可描述如下。

(2)目标函数f(X)如式(2)所示，求解目标为完成燃油转输的总时长最短：

(2)

式(2)中：T0为从巡航开始到燃油转输开启所需的时间；Wmain_ini为开始巡航时的基本油箱载油量；Waux为辅助油箱总的载油量。转输中断次数Npause由式(3)计算，“⎣」”表示向下取整。

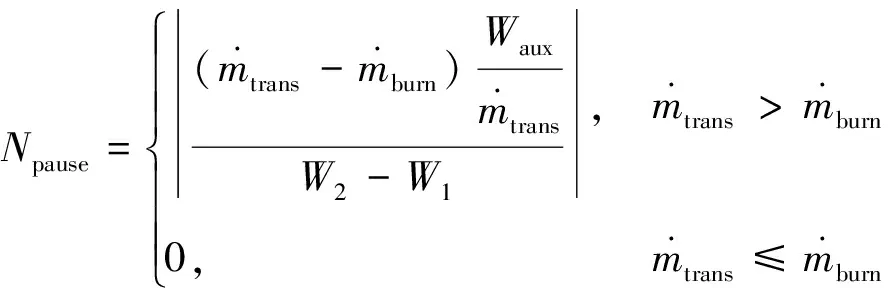
(3)

(3)约束条件1是当完成燃油从辅助油箱向基本油箱的转输时，基本油箱的载油量不少于备用油量，如式(4)所示：

(4)

(4)约束条件2是燃油转输中断的次数不大于预设值，即0≤Npause≤Nmax，如果要求燃油转输过程不得出现中断，则Npause=Nmax=0。

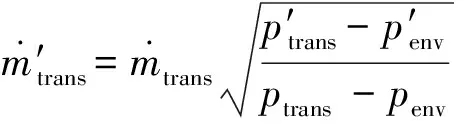
(5)

式(5)中：p′trans和ptrans分别为单、双发运行时的客舱压力；p′env和penv分别为单、双发运行时的外界大气压，客舱压力与飞行高度的关系为已知条件。

当单发运行时，在规定的时间Tsingle内，基本油箱的载油量不得下降至备用油量：

(6)

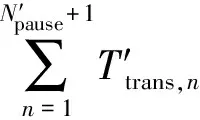
(7)

3 差分进化算法改进及验证

差分进化的基本原理是从随机生成的初始种群开始，通过反复进行变异、交叉和选择等操作来模仿生物界的进化过程，不断使种群中的个体向着适应环境的方向发展(保留适应环境的个体)，即逐渐逼近问题的最优解。文献[5, 6]对差分进化算法的概念、计算过程等进行了详尽的阐述，不再赘述。为了达到更好的算法稳定性与效率，在基本差分进化算法的基础上进行了改进。

3.1 改进差分进化算法

使用的改进差分进化算法的计算流程如图2所示。变异操作采用DE/best/2的差分形式，交叉操作采用二项式交叉，选择操作采用贪婪算法，迭代计算中采用精英保留策略。迭代过程将持续进行直到获得最优解或达到最大迭代次数限制。差分进化算法的基本概念和操作过程详见文献[6]，下面仅介绍本文对差分进化算法的改进。

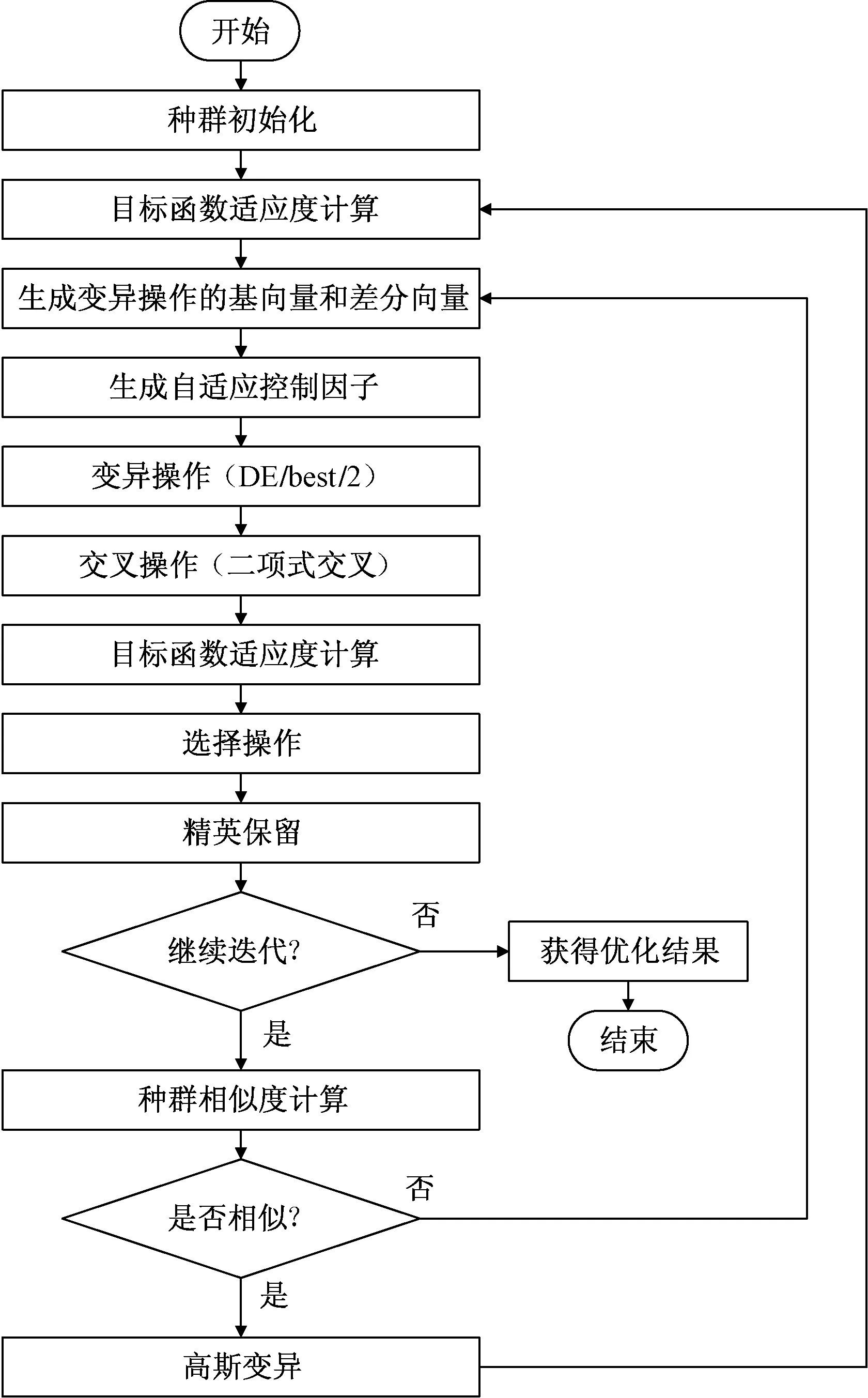
图2 改进差分进化算法计算流程Fig.2 The modified differential evolution algorithm calculation flow chart

3.1.1 基于自适应惩罚函数的适应度计算

为求解式(1)所示的约束优化问题，采用惩罚函数法将适应度函数fitness(X)构建为带有惩罚函数的非约束优化问题的目标函数fp(X)，如式(8)～式(10)所示。适应度函数最小值对应优化问题的最优解。构建目标函数时，将惩罚因子选取为关于自变量的函数[8]，以解决惩罚因子的确定问题。此外，为加快收敛速度，构建目标函数时，还借鉴了“多级惩罚”的思想[9]，即对违反约束大的段给予较大的惩罚而违反约束小的段给予较小的惩罚。

fitness(X)=fp(X)=f(X)+C(X)p(X)

(8)

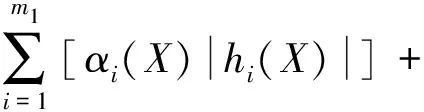
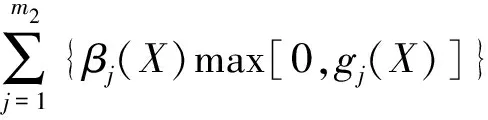
(9)

(10)

式中：C(X)为多级惩罚因子；p(X) 为惩罚函数；αi(X)和βj(X)为自适应惩罚因子，分别如式(11)和式(12)所示：

(11)

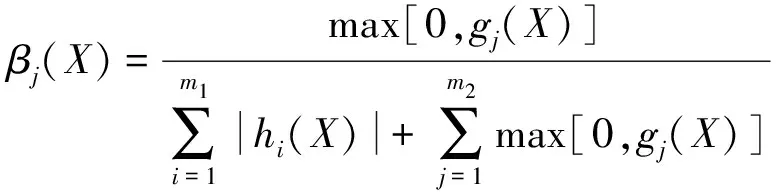
(12)

3.1.2 采用自适应缩放因子的变异操作

变异操作中，最重要的参数是缩放因子F，其取值对于种群的多样性有很大影响。采用基于种群个体适应度的时变计算策略，如式(13)所示[10]。

(13)

式(13)中：控制因子Fmax需预先给定数值；f(Xbest)为当前代种群中适应度最优个体的适应度，则参数Δfi和λ分别如式(14)和式(15)所示。

Δfi=|f(Xi)-f(Xbest)|

(14)

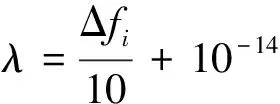
(15)

3.1.3 采用自适应交叉概率因子的交叉操作

交叉操作中，最重要的参数是交叉概率因子Cr。采用基于种群个体适应度的时变计算策略，如式(16)所示[11]。

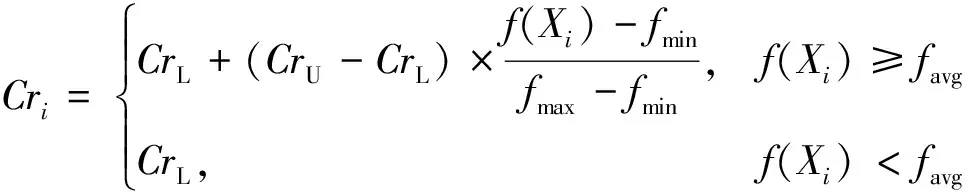
(16)

式(16)中：fmin、fmax和favg分别为种群个体的最小、最大和平均适应度；CrU和CrL分别为交叉概率因子上下限。

3.1.4 高斯变异

为了防止种群进化阶段陷入局部最优，补充了高斯变异操作[12]。针对当前种群适应度最优的个体，通过高斯变异产生一个新的最优个体，将二者中适应度更好的个体作为最终的当前代最优个体。该操作并非每一次计算都进行，而只在种群相似度达到一定程度之后才进行。

从差分进化算法的角度来看，一组优化变量值就代表了种群中的一个个体，即一个燃油转输参数候选方案；将燃油转输计算过程作为优化问题的适应度函数，通过对目标函数最佳适应度的计算获得最优的燃油转输参数方案。

3.2 数值实验

为了验证发展的改进差分进化算法对求解约束优化问题的有效性，使用以下典型测试函数对算法进行测试。文献[13]对这些测试函数进行了图形化显示。

(1)测试函数1：Sphere函数为

(17)

式(17)中：D为维数。该函数理论最优值为0，对应的最优点xi=0。

(2)测试函数2：Rosenbrock函数为

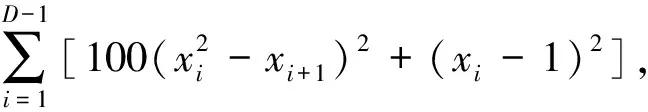
xi∈[-2.048,2.048]

(18)

该函数理论最优值为0，对应的最优点xi=1。

(3)测试函数3：Rastrigin函数为

xi∈[-5.12,5.12]

(19)

该函数理论最优值为0，对应的最优点xi=0。

(4)测试函数4：Ackley函数为

xi∈[-32,32]

(20)

该函数理论最优值为0，对应的最优点xi=0。

数值实验中，维数D取为10，种群大小Np取为优化变量个数的10倍，即Np=100，缩放因子F的上限取为1.0，交叉概率因子Cr的上下限分别取为0.9和0.1，最大进化代数取为500。为了减小随机干扰，对每个问题都重复进行50次实验。

表1为本文算法对测试函数的计算情况。结果表明，本文发展的改进差分进化算法的求解情况较为理想，可有效求解约束优化问题。

表1 测试函数计算结果

4 辅助燃油系统燃油转输参数优化

基于上述改进差分进化算法，进行辅助燃油系统燃油转输参数优化计算分析。优化计算所需限制参数等计算输入如表2所示，燃油转输参数变化范围如表3所示。

表2 计算输入

表3 优化参数变量范围

优化计算过程中，燃油转输参数和优化问题适应度随进化代数的变化情况如图3～图6所示。可见，在500代进化计算内可以求得最优解，本文发展的改进差分进化算法对燃油转输参数方案的优化求解有效。

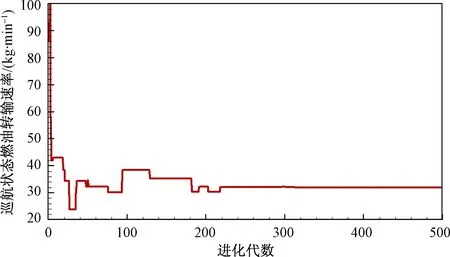
图3 巡航状态燃油转输速率随进化代数的变化情况Fig.3 Optimization calculation iteration history of the fuel transfer flowrate of cruise condition

图4 开启转输时的基本油箱载油量随进化代数的变化情况Fig.4 Optimization calculation iteration history of the main tank fuel quantity when fuel transfer starts

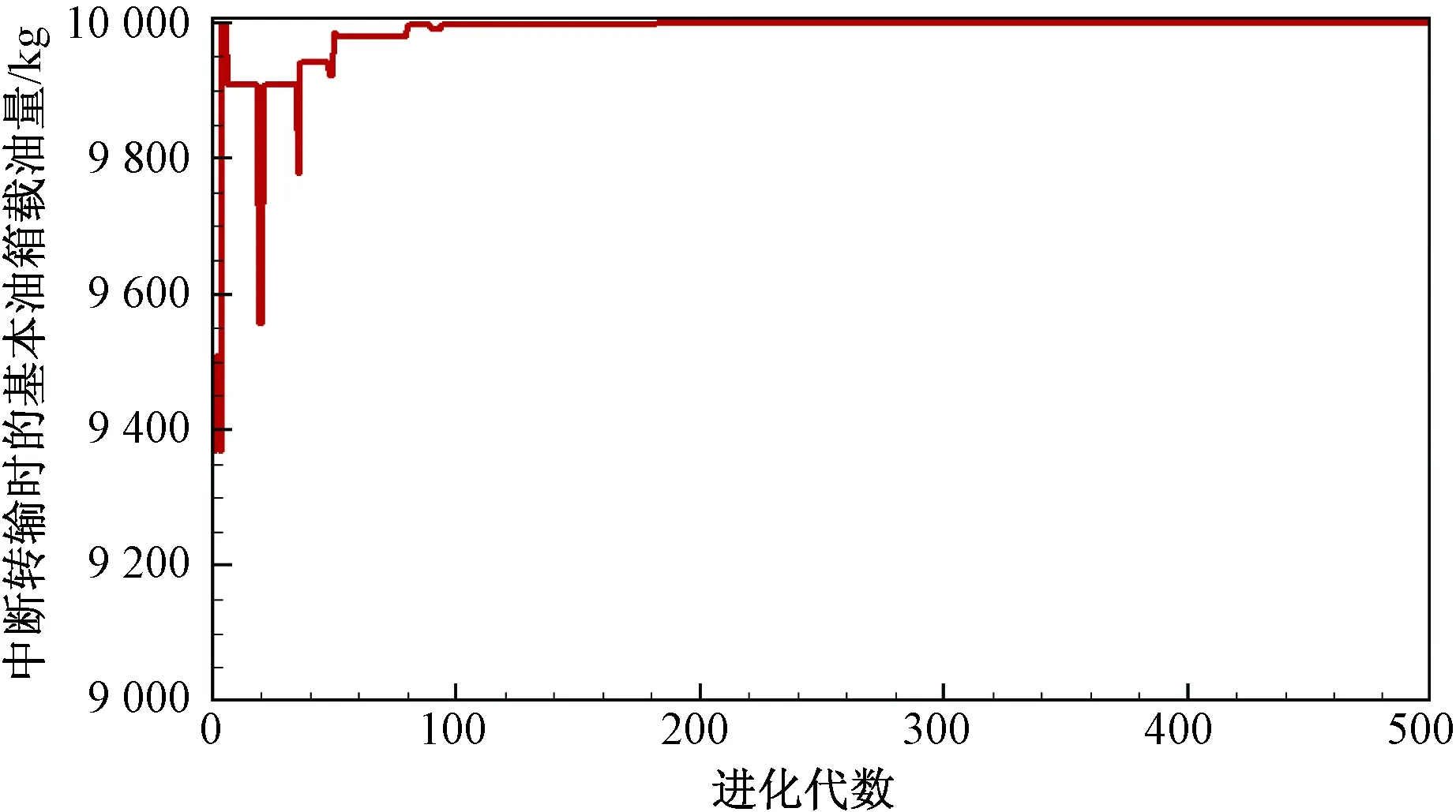
图5 中断转输时的基本油箱载油量随进化代数的变化情况Fig.5 Optimization calculation iteration history of the main tank fuel quantity when fuel transfer pauses

图6 适应度函数随进化代数的变化情况Fig.6 Optimization calculation iteration history of the fitness

优化计算得到的燃油转输参数方案及其燃油转输性能如表4所示。可以看出，优化计算结果可满足各项限制和优化约束条件。

基于表4中优化得到的燃油转输参数方案，对双发运行情况下的燃油转输过程可解析如下：①飞机经过10 min的双发运行，基本油箱的载油量从10 000 kg下降到9 700 kg；②此时，开启从辅助油箱向基本油箱的燃油转输；③以速率31.9 kg·min-1进行连续的燃油转输，转输过程持续157 min；④此时，基本油箱载油量上升至10 000 kg，燃油转输过程结束。

除了燃油转输参数方案优化计算结果以外，表4还列出了基于不同的燃油转输策略的计算结果。

对于双发运行的情况，各策略与最优方案对比如下：①策略一与最优方案相似，但由于转输速率低于最优方案，转输用时较最优方案多10 min；②策略二和策略三开启转输时的基本油箱载油量与最优方案相同，但转输速率远高于最优方案，使得转输中断次数很多；③策略四、策略五和策略六开启转输时的基本油箱载油量低于最优方案，转输速率高于最优方案，转输过程存在一到两次的中断，由于转输开启前用时和转输中断等待用时较长，使得完成燃油转输所需时间多于最优方案；④策略七与最优方案相比，转输开启前无需等待，但由于燃油转输速率低于最优方案，使得转输用时较长。

表4 优化计算结果及与给定的燃油转输策略的对比

对于单发运行的情况，各策略与最优方案对比如下：①策略一与最优方案相似，但转输结束时基本油箱的载油量低于最优方案；②策略二和策略三转输中断次数较多；③策略四、策略五和策略六转输结束时的基本油箱载油量低于最优方案；④策略七为连续转输，转输结束时的基本油箱载油量与最优方案接近。

通过上述对比可知，燃油转输参数优化方案可以保证双发运行情况下和单发运行情况下的性能最优，体现在双发运行情况下完成燃油转输的总时长最短且转输中断次数最少，同时在单发运行情况下转输完成时的基本油箱载油量接近满油。

5 结论

对差分进化算法进行了改进，发展了辅助燃油系统燃油转输参数优化计算方法，在此基础上对燃油转输进行了优化计算。得出主要结论如下。

(1)在分析辅助燃油系统燃油转输工作原理的基础上，将燃油转输设计过程抽象成可求解的约束优化问题，为燃油转输参数优化提供了解决思路。

(2)对差分进化算法进行了改进，通过典型测试函数的测试，表明了所发展的改进差分进化算法对约束优化问题求解的有效性。

(3)在给定的计算输入和变量范围的情况下，使用改进差分进化算法计算得到了燃油转输参数最优方案，其燃油转输用时短，转输中断次数少，结束转输时基本油箱的载油量高。

(4)与给定的燃油转输策略的计算结果对比表明，燃油转输参数优化方案在双发运行和单发运行情况下的性能都优于其他转输策略。