基于边缘概率的层次交互式图像分割算法

薛丽霞, 孙 伟, 汪荣贵, 杨 娟, 胡 敏

(合肥工业大学 计算机与信息学院,安徽 合肥 230601)

图像分割是图像处理领域和计算机视觉领域中的经典难题之一,其目的是从图像中将感兴趣区域与其他部分进行分离并提取出来。随着计算机处理能力的提高以及对图像处理需求的增加,图像分割更是受到研究者们越来越多的关注,它是许多高层视觉任务的基础,如场景识别、图像理解、视频目标追踪等。由于自然图像类型的多样性以及内容的复杂性,再加上理想分割目标对于人类主观视觉感知的依赖性,完全自动式图像分割方法显然不具有较好的实用性。目前,融合用户先验知识的交互式分割已逐渐成为图像分割中流行的方法。文献[1]提出的Graph Cut方法将图割应用到灰度图像前景提取领域,用户只需指定一部分区域作为前景和背景;文献[2]提出的Grab Cut方法利用高斯混合模型对前景和背景的颜色空间进行建模,并采用迭代的图割进行图像分割。上述方法虽然能够实现较好的分割效果,但是都以像素为基本处理单元,在计算效率上很难满足实际应用要求。

2003年,文献[3]首次提出超像素概念,并将其应用于图像分割中。经过十几年的发展,超像素在图像分割领域中的应用日益广泛。基于图论的图像分割算法具有很好的代表性。文献[4]提出了懒人抠图(lazy snapping)技术,较之于Graph Cut[1],该方法利用watershed[5]作为预处理,将得到的超像素作为图的顶点并用于构建图模型;文献[6]使用Mean Shift[7]作为初始分割,并利用迭代的图割进行图像分割;文献[8]在基于Graph Cut框架的基础上,通过学习超像素间的相关性,并用它们作为相邻超像素间边的权值来构建超像素图。由于超像素的数量远远小于像素,图的规模将大大减小。基于区域合并的图像分割方法也是很好的例子。文献[9]提出了基于区域合并的最大相似度交互式分割算法(maximal similarity based region merging,MSRM),该算法使用Mean Shift对输入图像进行初始分割,并依据局部最大相似度合并策略实现区域合并;文献[10]对MSRM进行了改进,根据k-全局最大相似度合并策略(即每次区域合并时合并前k个最相似的区域)来完成图像分割。尽管这些基于区域合并的分割算法能够实现较好的分割性能,但在预处理阶段,超像素分割算法(如Mean Shift)通常会产生较多的超像素,使后续区域合并操作的代价大大增加,甚至降低了整个算法的执行效率。Mean Shift过分割图像如图1所示。

图1 原始图像以及对应的Mean Shift过分割图像

本文提出了一种新的基于边缘概率的层次交互式图像分割算法。利用一种性能优异的边缘检测算子[11](structured edge,SE)作为输入,得到边缘概率图,并作用于现有的超像素分割算法,实现对超像素的提纯;通过计算相邻区域之间的相似度,并依据全局最大相似度合并准则,采用区域邻接图[12](region adjacency graph, RAG)和最近邻图[13](nearest neighbor graph, NNG)来实现层次区域合并,提高区域合并操作的准确性。本文方法的流程如图2所示。

1 本文方法

本文方法主要概括为基于边缘概率的超像素分割算法、相邻区域间相似度计算和层次区域合并3个部分。

1.1 基于边缘概率的超像素分割算法

1.1.1 人工标记的超像素分割

本文给出了超像素提纯的流程,如图3所示。在实验中,采用Mean Shift生成初始过分割区域(即超像素),为了对图像进行标记,用户可以输入任何线条、曲线和笔触来指定目标和背景。本文分别使用绿色、蓝色标注所有的初始目标区域和初始背景区域,如图3b所示。若一个区域中含有绿色目标标记的像素点,则该区域为目标区域;若一个区域中含有蓝色背景标记的像素点,则该区域为背景区域;剩余的所有区域为无标记区域。通常,用户只需标记部分目标区域和背景区域。如果用户指定的先验信息越少,那么交互式算法的鲁棒性越强。

用户标记完之后,共有带标记的目标区域、带标记的背景区域、无标记区域3种不同标签类型的区域,分别记为MO、MB、U。所有的目标区域都应该具有相同的标记,所有的背景区域以及无标记区域亦然。

1.1.2 SE+超像素分割算法

实验中发现大部分相邻超像素之间的边界并非真实目标轮廓。因此,为了更好地提纯超像素,本文引入结构化边缘检测算子SE[11]。相比于其他方法[14-15],SE法极大地提高了检测速度。在检测阶段,1个32×32图像块的特征向量X∈R32×32×K(K为通道数目)输入到结构化随机森林中,通过联合多棵决策树的输出结果可以得到图像的边缘概率。对于像素点(i,j),将它的边缘概率值记为Pb(i,j)。图像bird的边缘概率图如图3c所示。每个像素点的边缘概率取值范围为[0,1]。像素点的边缘概率值越大,表明其属于真实目标轮廓的可能性就越大,反之则越小。

对于图像的边缘概率图,对其进行二值化操作可得边缘二值图,即

(1)

其中,b(i,j)表示像素点(i，j)的二元取值0或255;T为SE阈值。在实验中,使用边缘概率图的边缘概率均值作为阈值T的值。

利用(1)式对边缘概率图执行阈值操作可得边缘二值图,如图3d所示。此外,对于相邻超像素R、Q,需要知道边界处的像素点是否位于真实目标轮廓。定义如下:

(2)

其中,e(i,j)表示像素点(i,j)是否位于真实目标轮廓;(i,j)∈lRQ,lRQ为R与Q之间公共边界处的像素点集合。

为了判断相邻超像素R、Q是否被合并,定义R、Q的边界强度arcRQ为:

(3)

若arcRQ>0,则R与Q不合并;否则R与Q合并。

联合(1)～(3)式,最终可以得到提纯后的超像素图,如图3e所示。

1.2 区域的内容表达与相似度度量

为了更好地指导后续合并操作,使用归一化的颜色直方图作为区域的特征描述符。首先,将RGB空间中的每个颜色分量都量化为16级,因此在特征空间中共有16×16×16=4 096个通道可以用来描述区域。则区域R可以表示为:

(4)

本文选择巴氏系数[16]度量区域R、区域Q的相似度。由于区域合并过程中仅合并相邻的2个区域,对于不相邻的2个区域,它们之间的相似度置为0。则区域R、区域Q的相似度定义为:

ρ(R,Q)=

(5)

1.3 层次区域合并

本文利用RAG和NNG来实现层次区域合并。RAG表示区域间的拓扑关系,NNG则对区域间的拓扑关系进行抽样简化,反映了合并的顺序。通过RAG与NNG的联合,本文构建了一个快速、高效的区域合并方法。

RAG为无向简单图,其顶点为区域,边为拓扑关系。一幅m个区域的图像可以表示为G=(V,E)。其中,V={v1,v2,…,vm},为图像的顶点集,表示图像的区域;E表示图像的区域相邻连接关系,E⊂V×V，在图结构中为边集,其权重w(vi,vj)为区域之间的相似度,可由(5)式计算。本文给出了一个区域划分以及对应的区域邻接图,如图4所示。

图4 区域划分以及对应的区域邻接图

在区域合并过程中,通过寻找RAG中的全局最大相似度边,并将相应顶点进行合并,更新RAG。如此反复执行,最终可实现图像分割任务。但是在寻找全局最大相似度边时,需要不断对边集进行排序,这是一个极为耗时的过程。另外,在区域合并时,只有部分区域的拓扑结构发生改变,此时只会影响RAG部分边的权值。NNG则是简化区域间的拓扑关系,仅保留每个顶点中最大相似度的边描述图像区域。对于给定的RAG图G=(V,E),NNG为有向图Gm=(Vm,Em),其中Vm=V,边集合Em可表示为:

Em={(vi,vj)|wm(vi,vj)=

maxw(vi,vk),(vi,vk)∈E}

(6)

其中,wm(vi,vj)为顶点vi相关联的指向其最相近区域vj的最大相似度边。对于NNG图的顶点序列,若始点与终点相一致,则称其为环。图4b对应的一个可能的NNG图，如图5所示。由图5可知,顶点序列v4v5v4(或v5v4v5)为环,v4与v5为2个区域互为最相似的区域,即该NNG中拓扑子图的最优合并区域对。

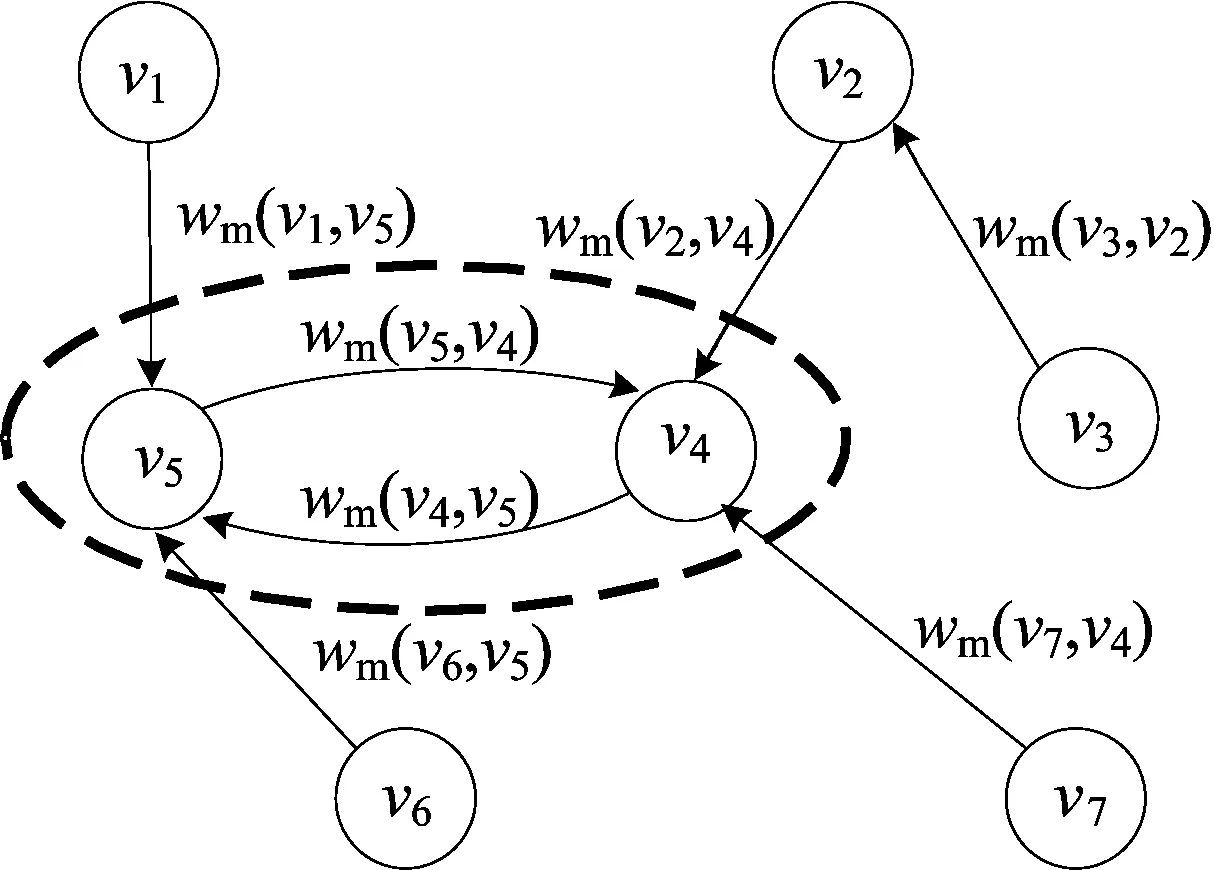
图5 最近邻图

易证得NNG的下列性质[13]:

(1) 沿着边的方向,权值逐渐减小。

(2) 环的最大长度为2。

(3) 至少存在1个子图,即至少有1个环。

由性质(3)可知,若NNG中不存在环,则区域合并将终止,即在区域合并终止之前,总能找到至少一个区域对进行合并。由性质(4)可知,NNG中环集合的数量小于边的数量,因而其搜索和排序的时间都将大幅降低。在合并期间,只需要维持NNG环,而不必对整个RAG进行搜索。初始的RAG来源于过分割图像,在搜索每个顶点的最相似邻域时形成NNG。在对NNG进行扫描时可发现NNG环。当区域合并终止时,所有的目标(背景)都被标记为目标(背景)标签,此时的目标区域轮廓即为待提取目标的轮廓。

2 实 验

为了评估本文方法的分割性能,选择Grab Cut[2]、GSC[17]、 MSRM、CRCM[18]4种不同的分割算法进行对比。实验中所有图像来源于MSRM分割图像库[9]和ASD自然图像库[19]。ASD自然图像库包含1 000幅自然图像和1 000幅人工标记的真实分割图像。

本文的实验平台为Matlab 7.12,操作系统为Windows 7 64 bit,CPU为双核2.60 GHz,RAM为4 G。

2.1 过分割区域数量对比

为了验证本文提出的SE+超像素分割算法的有效性,选择Mean Shift与SE+Mean Shift进行对比。实验中选用ASD自然图像库作为测试数据集。本文从ASD自然图像库中选取5幅自然图像作为初始分割结果展示,相应图像的Mean Shift和SE+Mean Shift过分割结果如图6所示。2种算法的初始过分割区域平均数量对比见表1所列。从实验结果来看,SE+Mean Shift能够产生更少的过分割区域,并且仍能保持较强的边界一致性。值得注意的是,本文提出的SE+超像素分割算法具有较强的普适性。当前其他一些应用较为广泛的初始过分割算法如watershed[5]、SLIC[20]等,也可以应用于本文提出的SE+超像素分割算法模型中。

图6 Mean Shift和SE+Mean Shift过分割结果

表1 2种算法的初始过分割区域平均数量对比

2.2 本文方法与其他方法的对比

为了对分割质量进行定量分析,本文以人工分割的结果作为理想情况,并参考文献[21]的方法,使用查准率P、查全率R、F度量进行评估。查准率P代表当前分割结果中准确分割所占的比例;查全率R代表此准确分割部分在理想分割结果中所占的比例;而F度量则为查准率P与R的线性加权(加权系数参考文献[21],设定α=1)。F度量所表示的综合指标值越大,则分割结果越符合人类视觉的主观目标判断准则。定义如下:

(7)

(8)

(9)

其中,N(PG)为真实目标区域的像素点数目;N(PO)为由算法计算得到的目标区域的像素点数目;N(PO∩PG)为真实目标区域与算法计算得到的目标区域之间的重叠像素点数目。

实验比较了本文方法与其他4种分割算法在ASD自然图像库上的分割性能,结果见表2所列。所有实验均在相同的人工标记下执行。

表2 不同方法在ASD自然图像库上的分割性能对比 %

由表2可知,本文方法的分割性能优于其他4种分割算法；而且本文方法具有最高的F度量,并且比MSRM高出1%。由于对超像素进行了有效的提纯,本文方法在执行效率上比MSRM更高效。尽管本文方法的分割性能优于竞争对手,但是当输入图像带有噪声或者由SE产生的边缘不是很明显时,本文方法的分割性能可能会受到影响。为了直观地展示图像分割结果,给出了5张原始图像以及对应的本文方法分割结果,如图7所示。

图7 原始图像以及本文方法的分割结果

2.3 不同颜色空间和相似度度量准则下的分割

2.2节的实验已经表明了本文方法在RGB颜色空间具有令人满意的分割性能,下面将测试本文方法其他颜色空间是否也具有较为理想的分割效果。分别将RGB颜色空间转化成HSI和LAB颜色空间。对于这2种颜色空间,仍使用HSI和LAB颜色直方图以及巴氏系数来计算相邻区域间的相似度。本文方法在图像bird上的分割结果如图8所示。从图8可以看出,基于HSI和LAB颜色空间的分割结果与基于RGB颜色空间的几乎一致,说明本文方法在不同颜色空间下都具有不错的分割性能。

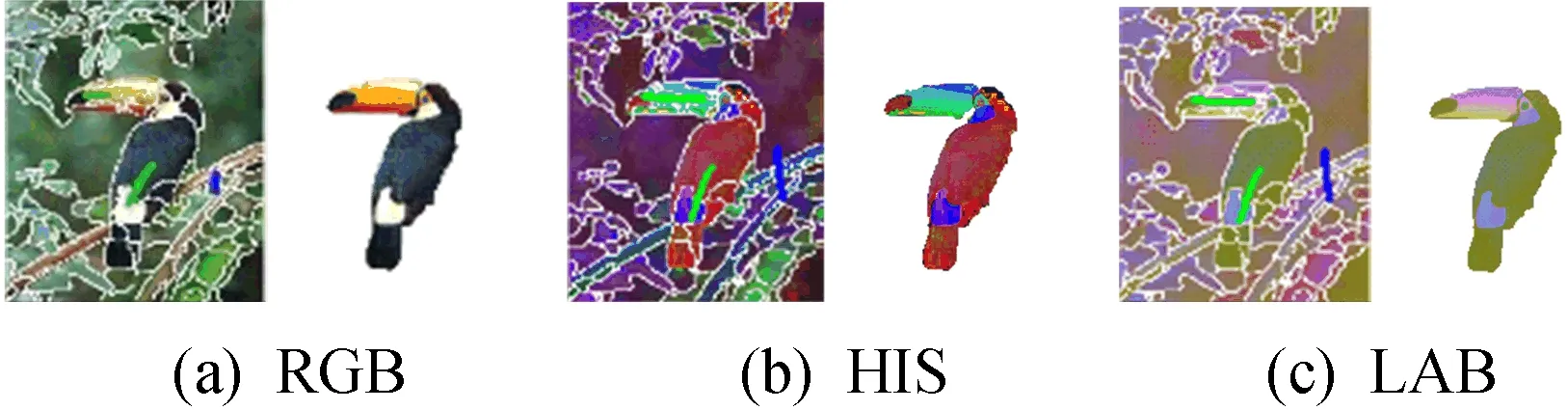
图8 本文方法在3种不同颜色空间下的分割结果

采用不同的相似度度量准则测试本文方法的分割效果。实验仍使用RGB颜色直方图,但利用欧式距离替换巴氏系数作为相似度度量准则。区域R、区域Q之间的欧式距离定义如下:

(10)

本文方法在图像dogs上的分割结果如图9所示。从图9可以看出,基于欧式距离的分割结果与基于巴氏系数的基本类似。可见本文方法在不同相似度度量准则下都具有较好的分割结果。

图9 2种不同相似度度量准则下的分割结果

2.4 本文方法的鲁棒性分析

本文方法是一种交互式方法,用户输入的先验信息对算法性能有着较大程度的影响。通常,只要用户标记的区域能够很好地覆盖主要特征区域,目标区域基本都能被准确地提取出来。

图像plane的初始分割以及图像分割结果如图10所示。图像plane的主要特征区域为机翼、机身、尾翼等,只需对这些主要特征区域进行简单的人工标记即可实现较为理想的分割效果。但对于复杂的图像,往往需要更多的用户输入。2组不同人工标记下的分割结果如图11所示。在图11a左半部分,左上角和右下角部分目标和背景较为相似,使得本文方法未能完整地提取出目标区域;在增加了一些额外的用户输入后,本文方法最终可以完整地提取出目标区域,如图11b右半部分所示。

图10 图像plane的初始分割以及图像分割结果

图11 2组不同人工标记下的分割结果

本文方法尽管在大部分情形下可以实现令人满意的结果,但若目标和背景极为相似或者初始分割质量不是太好,则不能取得较好的分割效果。本文方法2个失败的例子如图12 所示。

图12 本文方法2个失败的例子

在图12a左半部分,部分目标与背景极为相似(2点钟、4点钟、5点钟方向),即便使用了较多的用户输入先验信息,但最终的分割效果仍难以令人满意;在图12b左半部分,由于初始分割算法的目标边界一致性不是很好,临近目标边缘的部分区域既包含了目标也包含了背景(8点钟方向),导致最终的分割结果不是很理想。幸运的是,图12a左半部分的分割结果可以通过增加更多的用户输入来改善,例如对于靠近目标边缘的区域给与更多的用户标记;图12b左半部分的分割结果可以通过调整初始分割算法参数加以改进。对于初始分割算法的进一步研究将会改善初始分割质量,从而提高本文方法的鲁棒性。

3 结 论

本文提出了一种新的基于边缘概率的层次交互式图像分割算法。在初始分割阶段,本文利用SE提纯人工标记的超像素图,得到的超像素数量较少且边界一致性较好。在区域合并阶段,利用RAG和NNG实现了快速、高效的区域合并。由于初始的超像素被进一步提纯,本文方法的层次区域合并代价明显降低,算法执行效率大大增加。仿真实验结果表明,本文方法的鲁棒性、分割性能更好。

本文方法的最终分割结果依赖于初始过分割质量,后续工作是研究如何进一步改进超像素分割算法。另外,本文方法仅使用颜色直方图作为超像素的内容表达,接下来将研究如何使用更加有效的特征对超像素进行描述。