构建“数学模型”,求解“最小值”问题

江苏省海门市能仁中学(226100) 仇建新

关于用数学模型方法处理实际问题的过程,可以用图1表示.

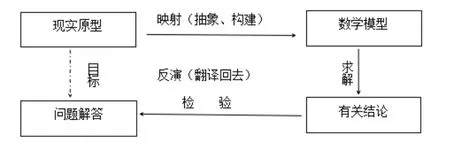
图1

其一,了解经典数学几何模型——“胡不归”模型的相关背景:相传一个身处异乡的小伙子,得知父亲病危的消息后便日夜兼程.然而,当他气喘吁吁地赶到父亲面前时,老人刚刚咽气！周围人告诉他,在弥留之际,老人不断喃喃地叨念“胡不归、胡不归?”

早期数学家曾为这则古老传说中的小伙子设想了一条路线(如图2),A是出发地,B是目的地,AC是一条驿道,而驿道靠目的地的一侧是沙土地带.为了急切回家,小伙子选择了线段AB.但是,他忽略了在驿道行走要比在沙土地带行走更快的因素.若他事先设计一条最合适的路线(尽管该路线长一些,但速度可以加快),是可以提前抵达家门口的.那么,他该选择哪条路线呢?

图2

其二,由现实情境抽象并构建“胡不归”数学模型,总结与归纳一般求解步骤及其依据:假设在驿道、沙地上行走速度分别为v1,(v1＞v2),在AC上任取一点D,设小伙子从A行走到D的路程AD,然后从D折往B路程为DB,则由A-D-B累计时间:.故此类问题关键在于如何找出点D,使得的值最小,这即是古老的“胡不归”问题.为此,我们归纳求解其“最小值”问题的一般步骤:

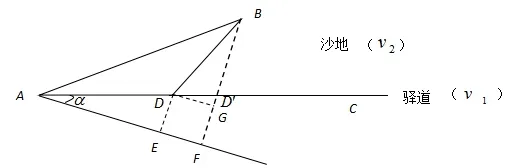
图3

第一步,在AD的一侧、BD的另一侧(如图3),设法构造一个锐角α,使得

第二步,过点B作新构造锐角α一边的垂线,垂足为点F,该垂线段BF的长度即为所求最小值;

第三步,代入上面有关式子进行计算.

解释第二步最小值的理论依据:易证四边形DEFG是矩形,得DE=FG,在RtΔAED中,sinα=sin ∠DAE=因此,+BD=sinα·AD+BD=DE+BD=FG+BD≥FG+BG=BF,当D运动到与点D′重合时,三点B,D′,F共线(恰好取“=”号),此时,根据“垂线段最短”得

其三,化归“胡不归”问题来探究“PA+K·PB”型最小值问题的几何模型(如图4)和数学原理(方法):

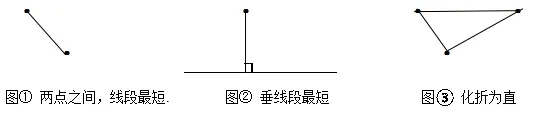
图4

当K=1 时,转化为“PA+PB”的最小值问题,即为“将军饮马”问题;

当1 且为正数时,按动点P 的运动轨迹分类:

(1)点P在直线上运动的类型称之为“胡不归”问题(如图5的①);

(2)点P在圆周上运动的类型称之为“阿氏圆”问题(如图5的②)

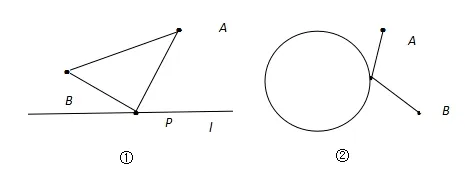
图5

其四,以中考数学真题为例侧重研讨以“胡不归”问题求解“PA+K·PB”型的最小值.

例题1(2019年成都中考数学B 卷第24 题)如图6,在边长为1 的菱形ABCD中,∠ABC=60°,将ΔABD沿射线BD的方向平移得到△A′B′D′,分别连接A′C,A′D,B′C,则A′C+B′C的最小值为:_____.

图6

评析由求“A′C+B′C的最小值”的数量关系,联想“胡不归”(K=1)的特例——将军饮马问题的几何模型,双动点A′,B′分别与定点C的距离的和的最小值,关键如何构造点C所在的定直线a,以及这两个动点(与a同侧)利用(与a)轴对称使之变为(与a异侧)“两点之间,线段最短”(如图6左图),过C点作BD的平行线l(定直线),以l为对称轴作B点的对称点B1,连接AB1交直线l于点C1,根据平移性质和轴对称性质可知A′C+B′C=AC1+BC1,当三点A,B1,C1=共线时AC1+BC1=AC1+B1C1取最小值,即AB1,根据已知可得AB=BB1=1,再解等腰三角形ABB1,此时BC ⊥AB1,根据勾股定理得,AB1=故答案为

这里的双动点A′,B′分别转化为双定点A,B,而定点C对应转化为动点C1(由将军饮马几何模型确定),此步最为关键,通过“形”来解“数”,将线段AC′与B′C的折线位置关系通过以上方法化归为线段AC1与B1C1的共线关系,事实上AB1与A′B′′也是相等的数量关系,最后利用“胡不归”模型求解.

例题2(2019年绵阳中考数学第24 题)在平面直角坐标系中,将二次函数y=ax2(a ＞0)的图象向右平移1 个单位,再向下平移2 个单位,得到如图所示的抛物线,该抛物线与x轴交于点A,B(点A在点B的左侧),OA=1,经过点A的一次函数y=kx+b(k≠0)的图象与y轴正半轴交于点C,且与抛物线的另一个交点为D,ΔABD的面积为5．

(1)求抛物线和一次函数的解析式;

(2)抛物线上的动点E在一次函数的图象下方,求ΔACE面积的最大值,并求出此时点E的坐标;

(3)若点P为x轴上任意一点,在(2) 的结论下,求PE+PA的最小值．

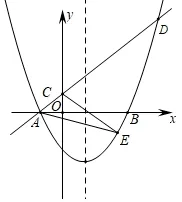
图7

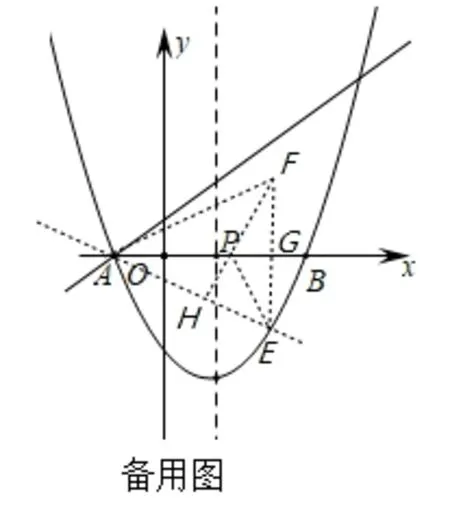
图8

评析(1)考查待定系数法求函数解析式,渗透数形结合思想,抛物线的解析式为即：直线AD的解析式为;(2)利用“参数法”设点则构建“二次函数模型”求解(面积的) 最大值问题,S△ACE=时,ΔACE的面积有最大值,最大值是此时点E坐标为(); (3)转化“胡不归”问题求解最小值的一般步骤,第一步探求sin ∠BAE=(具备sinα是前提),第二步作点E关于x轴的对称点F,连接EF交x轴于点G,过点F作FH ⊥AE于点H(构造了“PA+K· PB”型最小值问题的几何模型,是关键),交x轴于点P(如备用图),此时点F,P,H共线,=(PF+sin ∠BAE·AP)最小值=(PF+PH)最小值=FH,由“两点间距离公式”计算再由面积法AE·FH=EF·AG得FH=3.

从上面的例子看出,构建恰当的“数学模型”,是学习和研究数学的一种重要途径,既可以启发解题路思,处理数学个别问题,又可用来指导数学发现,和揭示解题规律、渗透数学思想及方法等.化归“胡不归”问题求解“PA+K·PB”型最小值问题的方法,本质上是初中数学“构造法”在不同层次上的应用之一,望多加体会！