典型缺陷车轴应力分布及对疲劳性能影响研究

2020-04-08任尊松吕晓旭李秋泽

北京交通大学学报 2020年1期

任尊松，吕晓旭，李秋泽

(1.北京交通大学机械与电子控制工程学院，北京 100044；2. 中车长春轨道客车股份有限公司国家轨道客车工程研究中心，长春 130062)

复兴号标准动车组正式运营标志着我国高速铁路发展迈入了新的阶段.在高速铁路快速发展的同时，高速动车组的运行安全性问题不容忽视，需确认其每一部件的结构可靠性，否则极可能会造成难以估量的后果.车轴作为高速动车组的关键承载部件，伴随列车的高速化和服役环境日趋复杂化，不可避免地产生异常损伤，如车轴击伤.在旋转弯曲载荷作用下，缺口处易萌生裂纹，进而会对车轴正常服役带来巨大安全隐患[1-2].

传统的车轴设计方法是将材料视为无缺陷的均匀连续体，通过加载求得结构中的最大应力，再根据最大应力小于材料许用应力的原则进行设计[3].对于实际服役的构件，总是不可避免地会出现各种形式的缺陷，使得结构强度远小于理论强度.因此，对于出现缺陷的车轴，传统的设计方法和运用经验已不再适用，必须开展基于断裂力学的损伤容限分析，采用更为科学准确的方法评估其安全性及可靠性[4].欧洲针对车轴从缺陷检测、断口形貌、载荷历程等方面建立起相对完善的评价体系，文献[5]研究了车轴半椭圆形裂纹的扩展，发现旋转弯曲的影响有限，而压装配合会对其造成更大影响；文献[6-8]概述了应用于铁路车轴的安全寿命和损伤容限方法.国内研究方面，文献[3]在考虑了车轮、齿轮和车轴压装配合效应和实测动应力的前提下，对带有缺陷的车轴的剩余寿命进行了研究，得出单个深度为300 μm撞击坑的空心车轴在正常服役期内不会发生裂纹萌生和扩展的结论；文献[9]从等效应力入手，发现车轴有缺陷时的等效应力大于等于疲劳极限；文献[10]建立了评估缺陷对表面淬火车轴疲劳性能影响的试验方法，系统地研究了飞石撞击缺陷对车轴材料疲劳性能的影响规律.但截至目前，关于缺陷具体尺寸参数对车轴结构强度和疲劳寿命的影响，并未有全面的研究.鉴于此，本文作者以某型车车轴实际应用为背景，针对撞击伤及凹槽型擦伤建立带有缺陷的高速动车组车轴有限元模型，采用数值仿真和理论计算方法，深入分析缺口尺寸参数对车轴应力分布的影响，并从S-N曲线变化对缺口造成的影响进行结构疲劳评估.

1 典型缺陷有限元模型

由于缺陷的差异，通过数值仿真和理论计算两种方法分别实现对撞击伤及凹槽型擦伤的有限元计算和研究.

1.1 撞击伤有限元模型

列车高速运行时，底部由于存在负压和涡状气流，导致线路路基上的砟石被气流带起，这一情况在线路积雪环境中更为明显和严峻，比重轻的雪被车下气流卷起，夹杂砟石，与车轴产生碰撞，造成车轴受到冲击损伤，因此动车和拖车车轴都有发生表面击伤的风险.考虑到拖车车轴有更大表面暴露在外部环境，发生撞击损伤的几率更高，实际运用过程中出现的车轴表面击伤次数更多，故以拖车车轴为对象对撞击伤引起的结构强度问题进行分析.

车轴异物损伤最可能的来源是道砟冲击，由于道砟形状各异，对车轴表面造成的缺口形状不尽相同，结合现场调研结果，且为方便研究，定义道砟冲击造成的缺口形状为三维半椭圆球体[11]，图1即为异物冲击缺口的简化模型.其中，a和b分别为平行于车轴表面方向椭圆的长、短半轴，c为沿垂直与车轴表面方向的缺口深度.

仿真分为两个步骤，先利用Hypermesh软件建立不含缺口的拖车车轴有限元模型，如图2所示.模型中，车轴采用较细致的网格进行划分，车轮除与车轴配合区需细化网格，其余区域网格较为粗略.网格类型选八节点六面体solid185，单元总数为495 600个，节点总数为555 600个.

再借助Franc3D软件在有限元模型中插入缺口，缺口位置选择在车轴轴身，即图2选中的灰色区域.Franc3D是三维断裂分析软件，主要用来计算工程结构在任意复杂几何形状、载荷条件和裂纹形态下的三维裂纹扩展的疲劳寿命.它基于有限元软件进行断裂力学计算，与Ansys、Abaqus和Nastran等有接口.Franc3D通过子模型技术插入裂纹或缺口，所有Franc3D支持的有限元软件均支持子模型.

实际分析时，裂纹或缺口尺寸相对于整体结构来说往往很小，所以Franc3D将网格重划区域限定在子模型内，这样可大大减少数据的传送和处理量，从而提高计算效率.其余部分的模型可包含简化的结构(如shell单元)、复杂边界条件(如接触)或完全六面体的网格模型，重划的子模型会被重新“放入”全局模型，再对整体模型进行分析[12].图3为建立的含撞击缺口的车轴有限元模型，左侧为模型全局图，右侧为缺口子模型局部图，可以看出Franc3D能较好实现缺口网格划分，且缺口处网格尺寸约为0.25mm.此外，子模型网格单元类型为四面体solid187，并通过五面体solid186与全局网格相连.

1.2 凹槽型擦伤有限元模型

列车运行过程中，异物长时间作用在车轴表面的摩擦力会造成车轴产生沿整个圆周方向的擦伤，或者是线路上的道砟被气流吸起卡在列车牵引电机外壳和车轴之间时，随着车轴高速旋转，会对轴身造成擦伤[13].此外经过调研，发现擦伤多出现在动车车轴上，故以动车车轴为对象对擦伤进行分析.

考虑擦伤异物的形状及作用时间，将缺陷形貌定义为V型缺口，深度为h，根部曲率半径为r.由于擦伤为绕车轴整个圆周方向，直接由CAD和Solidworks软件绘制擦伤车轴实体模型，再利用Hypermesh划分网格即可得到含擦伤车轴有限元模型，如图4所示.单元类型采用8节点6面体solid185单元，单元总数为312 240个，节点总数为357 480个.

2 缺口应力计算结果及分析

有限元计算时，考虑车轴悬挂件惯性载荷，不考虑制动影响.左侧车轮踏面处施加全约束，右侧车轮踏面处放开沿车轴横向的位移，并对车轴进行应力分析.缺口主要会引起应力集中，故以应力集中系数表征缺口对结构强度的影响.此外，缺口包含长度、宽度和深度等多组参数，通过设置不同的参数值，分析缺口引起的应力集中系数.

2.1 撞击伤参数的影响

根据生产企业提供的动车组车轴损伤型式归类统计研究报告，规定高速动车组车轴允许存在的异物冲击缺口的极限深度为1.5 mm；文献[14]指出，一旦发生飞石冲击，可能会在车轴表面留下最深可达2 mm的尖锐缺口.综合考虑各方面因素后，将模型中的车轴撞击缺口的最大深度取为2 mm.除撞击缺口深度c外，缺口长短半轴a、b的比值及入射角度λ也会造成影响，设置不同的参数分析撞击缺口对车轴应力分布的影响规律.

缺口长短半轴a、b分别取值2 mm和1 mm，入射角度λ定义为缺口长半轴与沿车轴横向的夹角，取0°、45°及90°共3组参数，深度c取0.25～2 mm共8组参数. 通过仿真计算，可得到不同缺口深度及入射角度对应的缺口应力集中系数，见图5.结果表明，缺口深度及入射角度都会影响缺口应力分布，且深度越深，角度越大，应力集中越明显.此外在缺口入射角度较小时，缺口深度的变化对应力集中系数的影响不明显.

为研究缺口形状的影响，深度c取为1 mm，入射角度λ取为90°，设置不同的a和b值，图6即为仿真所得4组参数下的缺口应力分布云图，结果表明缺口最大应力发生在沿椭圆长半轴方向的缺口根部，且往两侧应力逐渐递减.此外，椭圆缺口形状参数会显著影响缺口附近应力分布，椭圆长、短半轴比值越大，缺口处最大应力也表现出增大的趋势.

通过计算，可得到8组缺口参数对应的应力集中系数，见表1.结果表明，缺口形状显著影响应力分布，且长、短半轴比值越大，应力集中越严重，尤其是在缺口尺寸较小的情况下；当缺口尺寸不断增大时，长、短半轴比值所造成的应力集中有所降低.

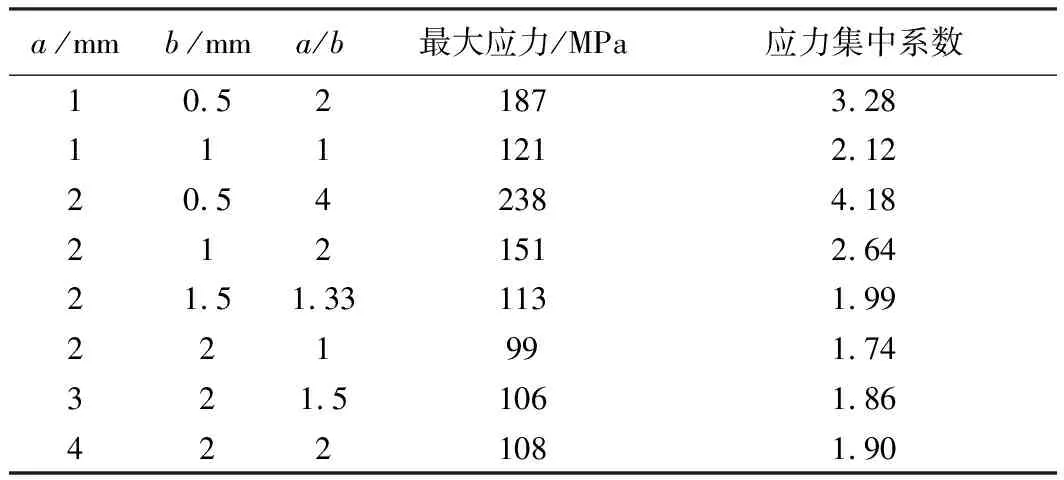
表1 不同形状比下的缺口应力集中系数

2.2 凹槽型擦伤参数的影响

依据生产企业高速动车组车轴损伤统计结果，规定车轴允许存在的凹槽型擦伤的极限深度为1.5 mm，考虑到该规定有一定的安全系数，将擦伤缺陷的极限深度同样取为2 mm.设置不同的缺陷深度及根部曲率半径，以研究擦伤对车轴应力的影响规律.

针对凹槽型擦伤，采用数值仿真方法得到应力集中系数，凹槽型擦伤计算可近似看成带有环状沟槽的圆杆的弯曲.设置一组参数进行对比，图7为有限元仿真结果.

由图7可知，最大应力发生在缺口根部，应力集中系数为3.1. 查阅应力集中系数手册[15],可得相同尺寸缺口下的应力集中系数约为3.2，两者结果近乎一致，表明有限元计算结果合理可信.

通过仿真方法获得了其余组参数对应的应力集中系数，见图8.结果表明，擦伤缺口深度h越深，根部曲率半径r越小，应力集中越明显；且当r小于0.4mm时，应力集中表现出明显的加剧现象.

3 缺口S-N曲线评估

为进一步评估缺陷对车轴结构可靠性的影响，对其疲劳性能进行分析.材料的疲劳性能由S-N曲线表征，一般通过小尺寸试件在旋转弯曲对称循环载荷作用下得到，可通过极限拉伸强度参数对其进行数值估计.根据生产企业反馈，该型号高速动车组车轴材料的极限拉伸强度Su=700 MPa，对于一般常用金属材料，在Su<1 400 MPa时，旋转弯曲载荷作用下的材料疲劳极限可估计为

Sf=0.5Su

(1)

若已知材料疲劳极限Sf和Su，S-N曲线可作偏于保守的估计，S-N曲线幂函数形式表达式为

Sm·N=C

(2)

式中：m和C为与材料相关的特征参数.在寿命N=1时，有

S1=Su

(3)

式中：S1为寿命N为1次时对应的疲劳强度，即单调载荷作用下，试件在极限强度下破坏.考虑到S-N曲线描述的是长寿命疲劳，不宜用N<103以下，故通常假定寿命N=103时，有

S103=0.9Su

(4)

对于金属材料，疲劳极限Sf所对应的循环次数一般为N=107次，考虑到估计Sf时的误差，作偏于保守的假定，在N=106时，有

S106=Sf

(5)

依据式(4)和式(5)可求得光滑车轴相关参数：m=11.75,C=7.9×1035.但对于存在缺口的构件，缺口应力集中将使其疲劳性能严重下降，需通过相关理论进行修正得到缺口的疲劳寿命曲线[16].

3.1 疲劳缺口系数的计算

为评估缺口车轴S-N曲线，首先需确定存在缺口时的疲劳缺口系数.Kt为应力集中系数，定义为缺口处最大实际应力σ与该处名义应力S之比；Kf为疲劳缺口系数，定义为光滑件疲劳极限Sf与缺口件疲劳极限Sf′之比.缺口应力集中使得疲劳强度下降，故Kf是反映缺口影响且大于1的系数，显然疲劳缺口系数Kf与应力集中系数Kt有关.Kt越大，应力集中越严重，疲劳寿命越短，Kf也就越大.但实验研究结果表明，Kf与Kt并不相等.因为应力集中系数Kt只依赖于构件的几何形状，而疲劳缺口系数Kf却与材料有关.

一般来说，Kf小于Kt，且二者之间关系为

q= (Kf-1)/(Kt-1)

(6)

当q=0时，Kf=1，Sf′ =Sf，缺口对疲劳性能无影响；当q=1时，Kf=Kt，Sf′ =Sf/Kt，缺口对疲劳性能影响严重，故称q为缺口敏感系数，其取值范围为0～1.在缺口最大实际应力不超过屈服应力的情况下，缺口敏感系数可用Neuber经验公式估计

q=1/(1+(d/r)1/2)

(7)

式中：d是与材料有关的特征长度.当材料极限拉伸强度为700 MPa时，特征长度参数d取0.16 mm.结合式(6)和式(7)，代入相关参数值，即可得到不同尺寸缺口对应的疲劳缺口系数，表2即为计算所得8组缺陷参数对应的疲劳缺口系数Kf.

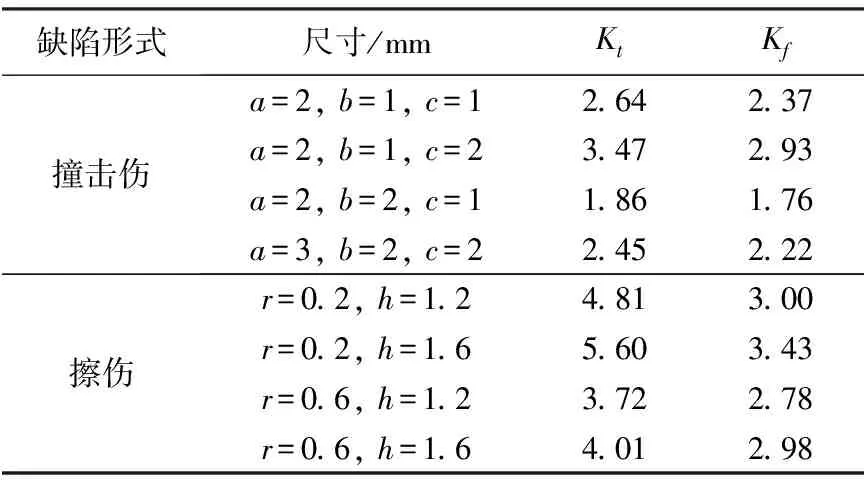
表2 不同缺陷参数对应的Kf

3.2 缺口S-N曲线的计算

确定疲劳缺口系数Kf后，即可估计缺口S-N曲线时，首先假定寿命N=103时，有

S103′=S103/Kf′

(8)

式中：Kf′为N=103时，光滑件疲劳强度与缺口件疲劳强度之比.假定寿命N=106时，有

Sf′ =Sf/Kf

(9)

若缺乏对于Kf′的估计，可以将式(8)的假定换为N=1，则有

S1′=Su

(10)

由此两点在双对数坐标上确定的直线，即为缺口S-N曲线.S-N曲线反映的是低应力、长寿命疲劳性能，因此所估计的S-N曲线只能用于估计长寿命即N>103的情况下.选取N为1及106两点，代入相关数值，即可得不同参数对应的缺口S-N曲线，图9给出了半对数坐标下无缺口及3组参数缺口对应的S-N曲线，结果表明缺口会影响车轴疲劳性能，且随着疲劳缺口系数的增加，曲线整体下移，疲劳性能受到显著影响.如当Kf=2.98、缺口应力幅值超过220 MPa时，车轴疲劳寿命对应的应力循环次数不超过104.