基于RBF神经网络的伊犁马体重估测模型

朱让东，张太红，郭 斌

(新疆农业大学 计算机与信息工程学院，新疆 乌鲁木齐 830001)

0 引 言

体重指标能够很好地反映动物健康状况，并且在动物的繁育管理、运动性能、肉质评价等方面都具有重要的参考价值。伊犁马作为国内优良的培育品种之一，是通过多品种长期杂交改良和选育而逐渐形成的中国特有马品种[1]。传统的伊犁马体重主要是通过地磅等工具进行直接称重，该方式易造成马匹产生应激性行为，不利于动物的健康养殖。已有研究表明[2-5]，动物的体重信息可以通过数学模型进行有效估测。中国农业科学院北京畜牧兽医研究所的侯浩宾对马、驴主要经济性状相关功能基因的研究进展进行了综述，通过论文可知马、驴等草食家畜体尺、体重由相关体型基因决定[6]。这为体重估测提供了理论依据。He等针对314匹伊犁马的体重、体高、胸围和管围进行关联分析，验证了LCORL基因表达水平与BIEC2-808543位点基因型显著相关[7]。新疆农业大学动物科学学院的杨文科，建立了三个估测成年母马体重的回归模型[8]。凉山州畜牧兽医科研所的杨世忠通过对成年建昌母马体尺体重的实测研究，得出多元线性回归比单回归估测的体重准确[9]。

目前，大部分的马体重公式还是以一元或多元线性回归模型为主，但是各体尺信息之间存在自相关性，势必会引发特征值之间的共线性问题，而运用神经网络模型估测体质量方面已有研究，其研究结果表明，通过RBF神经网络方法建模，消除了线性回归分析中自变量的共线性问题，预测结果优于回归模型[10]。从神经网络模型的角度来说，RBF神经网络模型是BP神经网络的一个分支，RBF神经网络模型具备计算量小、学习速度快、不易陷入局部极小等诸多特点[11-15]。该研究根据RBF神经网络方法，建立了伊犁马体重估测神经网络模型，为伊犁马利用体尺信息估测体重提供了新方法。

1 径向基函数(RBF)神经网络简介

1.1 模型简介

RBF神经网络是根据径向基函数特性构建成的神经网络，前人曾提出了多变量插值的径向基函数方法。径向基函数是实值函数，取值仅仅依赖于距离值。该类函数自变量离原点的距离(Φ(x)=Φ(‖x‖))，或者是离任意一点c的距离(Φ(x,c)=Φ(‖x-c‖))，在径向基函数神经网络中任意一点c也被称为中心点，因此任意满足Φ(x)=Φ(‖x‖)特性的函数Φ都可称之为径向基函数。径向基函数的距离计算可以采用任意距离函数，但一般使用欧氏距离(又称欧氏径向基函数)。RBF神经网络是一种高效的前馈式神经网络，其与BP神经网络结构类似，主要的不同之处在于隐含层中神经元处理数值的变换方式不同，BP神经网络是一个典型的全局逼近网络，而RBF神经网络是一个常见的局部逼近网络。RBF神经网络包含输入层、隐含层(径向基层)、输出层，特征值到隐含层的变换是非线性的，而输出结果是对隐含层各神经元的线性组合。RBF神经网络拥有对非线性函数极佳的逼近效果，以及全局最优的特性。该模型设计的RBF神经网络结构如图1所示，其中X1表示胸围、X2表示体高、X3表示体长。

图1 RBF神经网络

1.2 隐含层及神经元

RBF神经网络属于单隐含层的神经网络，其隐含层中的激活函数为径向基函数。根据隐含层中神经元的数量与输入层节点、样本数量的比较，RBF神经网络可分正则化RBF神经网络(输入样本与神经元个数相等)，以及广义RBF神经网络(输入层节点小于隐含层神经元个数)。该模型采用广义RBF神经网络，隐含层中神经元的个数大于输入层节点数。RBF神经网络将径向基函数作为神经元从而构成了隐含层空间，其中径向基函数隐含层可以将输入量直接映射到隐含层，而无需通过权值连接映射，将神经元固定后，输入层到隐含层之间的映射关系也将固定。该神经网络的输出值是神经元输出值的线性加权和，此处的权值即为神经网络可调参数，从而可知隐含层到输出层的映射关系是线性的。隐含层的作用是把向量从低维度的p映射到高维度的h，这样低维度线性不可分的情况到高维度就可以变得线性可分了，其也是核函数的主要思想。目前该模型的输入至输出的映射是非线性的，而该模型的输出对可调参数而言却又是线性的，因此权值就可由线性方程组直接解出，从而极大提高学习速度并避免局部极小问题。该模型将高斯核函数作为隐含层神经元，具体函数式如下：

(1)

其中，xi为输入值，lj为神经元中心点，‖xi-lj‖2为欧氏范数，σ为径向基函数的局部作用范围。

1.3 选择中心点

对中心点的选择，实验采用了K均值聚类算法，其核心思想是将相似点聚类起来。假设在训练集中存在相似的两个值x1≈x2，可预计其RBF神经网络预测值也相似，RBF(x,x1)≈RBF(x,x2)，将两点聚类得μ≈x1≈x2。聚类问题是将数据集合{xn}分成M个不相交的集合S1,S2,…,SM，每个集合Sm选择一个中心点μm表示该集合,使得任意xn∈Sm⟺μm≈xn。通过误差函数查看数据点到自己所属集合的距离平方和，可写成如下公式：

Ein(S1,…,SM;μ1,…,μM)=

(2)

聚类算法就是要最小化该目标函数，即解决如下最优问题

min{S1,…,SM;μ1,…,μM}=

(3)

由于S和μ属于不同的两种类型值，S1,S2,…,SM属于类型变量，μ1,μ2,…,μM属于数值变量。需先固定μ1,μ2,…,μM，为每个Xn找到最优Sm。接下来，固定S1,S2,…,SM选出每个类的代表值。此时，原始最优问题退化成了一个与μm有关的无限值最优化问题，因此，只需目标函数的梯度为0即可，即：

(4)

令上式为0，则μm是属于Sm的Xn的均值。总结其流程为：

(1)初始化μ1,μ2,…,μK，即在Xn中随机选取K个点，该模型选取点个数为17。

(2)交替最优化Ein，即重复以下过程直至收敛(S1,S2,…,SK,不再变化判定为收敛)。重复过程一：最优化S1,S2,…,SK,即把Xn分给离它最近的那个μi所属类簇。重复过程二：最优化μ1,μ2,…,μK,即对每个SK，求属于该类簇所有点的均值，因为这个过程中Ein一直在变小，因此该算法必然收敛。

2 估测模型训练过程

2.1 数据预处理

采集数据需进行清洗，补足缺省值，去除离群点，纠正因人工造成的误差。原始数据各特征之间散点图见图2。

图2 原始数据各特征之间散点图

根据中心极限定律，确保预测值(体重)符合正态分布(见图3)，否则需通过数据变换将待估测值进行正态化。随即将数据集进行划分，该实验将数据集划分为训练集及验证集两个部分，对训练集数据进行标准化、归一化处理。

图3 预测值(体重)呈现正态分布

2.2 特征值选择

根据皮尔逊积矩相关系数方法可以计算出各个特征之间联系的紧密程度，并将相关系数矩阵用热力图进行表示(见图4)。通过比较体尺与体重之间的相关系数，可知伊犁马的胸围与体重之间的联系最紧密，管围与体重之间的关系相对最小，因此，选择前三个相关性最密切的特征构成该模型的输入层，选择的特征分别为胸围、体高、体长。

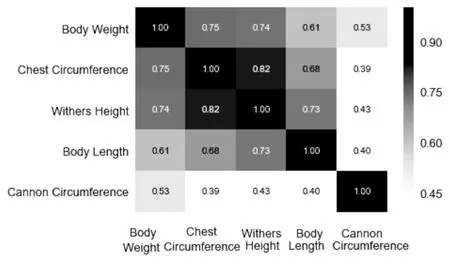
图4 特征值选择

2.3 训练过程

该模型先计算输入值到中心点的距离，然后使用高斯核函数进行变换，最后将神经元输出作线性累加求和，得到输出值。总结起来，RBF网络的假设函数如下：

(5)

其中，RBF为高斯核函数，μk为中心点，βk为权重。

根据式(5)，可得RBF神经网络的训练核心主要是两个部分，第一确定神经网络隐含层中心点，第二是确定神经网络隐含层神经元的权重。中心点的确定采用K均值聚类算法。神经元的权重是对经过RBF变换过的数据进行求解线性回归，即用平方误差作为误差函数，让算法优化系数βk。变换后的数据为：

zn=[RBF(xn,μ1),RBF(xn,μ2),…,RBF(xn,

μk)]∈N

(6)

可知最优的系数β=(ZTZ)-1ZTy，其中Z是对称方阵，因将高斯函数作为神经元函数，则Z还是可逆的，系数β可以继续简化成β=Z-1y。虽然神经网络模型具有过拟合的危险，但是该实验使用高斯核得到的核矩阵，并且通过减少中心点数量，使得网络模型正则化，避免了过拟合的情况。整体训练过程为：

(1)使用K均值聚类算法得到中心点{μk}；

(2)使用高斯函数围绕中心点μk构建变换∮(x)；

(3)变换后的数据运行线性模型，得权重β；

(4)结合权重返回最终的预测值。

3 实验结果与分析

3.1 实验数据集

实验数据源取自新疆伊犁种马场，实验对象为85匹一至三岁伊犁马，包括训练集70组数据，验证集15组数据。通过皮尺、测杖、磅秤等测量工具，采集马匹的体高、体长、管围、胸围，以及体重信息。采集日期为2018年3月，体重信息是在早晨马匹未出栏，无进食状态下进行采集。

3.2 实验方案及评价指标

首先进行数据采集，其次对采集数据进行清洗及预处理，并分析模型所需主成分，然后运用python语言结合第三方模块Scilkit-learn(sklearn)构建RBF神经网络，根据评价指标对模型进行参数优化，最后确定模型并与现有经验公式进行对比分析。

实验采用平均绝对离差(mean absolute error，MAE)来评价模型的估测精度。该评价方法是累加每个估测值与对应实际值之差的绝对值，再进行求平均。假若验证集实际值为X={X1,X2,…,X15}，对应模型的预测值为Y={Y1,Y2,…,Y15}，则平均绝对离差可以表示为：

(7)

同时，实验还通过线性拟合优度R2对模型线性估测进行评价，R2的取值范围为0至1，越接近1，说明拟合效果越好。假若验证集实际值为X={X1,X2,…,X15}，对应模型的预测值为Y={Y1,Y2,…,Y15}，则可知拟合优度公式为：

(8)

残差平方和(error sum of squares，SSE)为：

(9)

总偏差平方和(total sum of squares，SST)为：

(10)

预测值平均公式为：

(11)

3.3 实验结果

经过多次实验(见表1)，确定当神经网络模型隐含层神经元个数为17，学习步长为0.001时效果最优。

表1 隐含层及输出层各神经元的权值计算结果

此时RBF神经网络估测模型的平均绝对离差为7.75 kg，拟合优度R2为0.917，伊犁马体重线性回归估测模型的平均绝对离差为15.45 kg，拟合优度R2为0.688。将RBF神经网络模型与线性回归模型相比，在平均绝对离差方面RBF神经网络模型降低了7.7 kg，在拟合优度R2方面提升了0.229。RBF神经网络模型预测值与实际值的线性拟合效果如图5所示。

3.4 与现有体重模型对比

查阅相关资料，可得通用性马体重估测模型如下：

模型Ⅰ：Y1=X1×5.3-505[16]；

模型Ⅱ：Y2=X1×X2×0.016[17]；

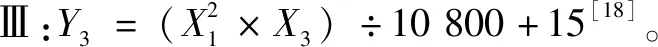
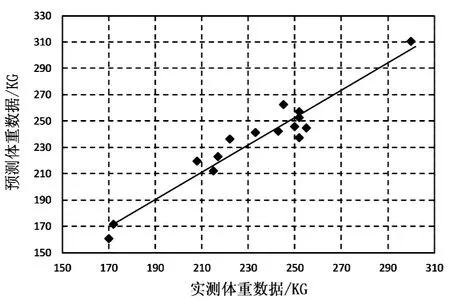
图5 RBF神经网络模型预测值与实测值回归分析

利用15组测试集数据，分别对线性回归模型、RBF神经网络模型、通用模型Ⅰ、模型Ⅱ、模型Ⅲ进行估测效果对比(见表2)。

表2 多模型预测结果 kg

根据测试数据可知，当前测量伊犁马平均实际体重数据值为232.4 kg，而线性回归模型估测体重平均值为240.563 kg，径向基函数RBF神经网络模型估测体重平均值为234.461 kg，通用模型Ⅰ、模型Ⅱ、模型Ⅲ分别估测体重的平均值为247.247 kg、296.151 kg及271.484 kg。在伊犁马体重平均值方面，径向基函数RBF神经网络模型，相较于其他体重估测模型最接近实际马匹平均体重。在伊犁马体重平均绝对离差方面，模型依次平均绝对离差值为15.446 kg、7.754 93 kg、21.5 kg、63.751 5 kg及39.084 kg，估测效果最优的是RBF神经网络模型。在两种评价指标中，表现最优的为RBF神经网络模型。因此，在五类马匹体重估测模型中RBF神经网络模型估测的体重值总体水平优于其他模型且最接近实际体重值。根据比较分析平均数以及平均绝对离差可知，模型Ⅱ估测伊犁马体重效果欠佳，认为不具备客观反映伊犁马体重的能力，参考价值不高。

4 结束语

文中用70匹伊犁马体尺、体重数据作为训练集，以高斯函数作为神经元，用K均值聚类方法找寻中心点，建立了关于伊犁马体重估测的RBF神经网络模型。结合通用性马匹体重估测公式、线性回归模型及RBF神经网络模型，在验证集上进行对比分析发现，RBF神经网络模型估测效果最优，平均绝对离差为7.75，线性回归拟合优度为0.917，估测效果优于马体重估测线性回归模型，明显优于其他通用性马体重估测模型。通过构建RBF神经网络伊犁马体重估测模型，分析发现RBF神经网络方法能够在一定程度上消除特征值之间的共线性问题，可以应用到伊犁马的体重估测中。