作业型水下机器人姿态调节控制研究
2020-04-08周克秋李钦奉
周克秋,李钦奉
(江苏科技大学 机械工程学院,江苏 镇江 212003)
0 引 言
新世纪以来,中国加大了对海洋资源的勘探开发,水下机器人(remote operated vehicle,ROV)的研究逐步成为热点。其在水下搜救打捞、海洋油气管道维修、能源勘探等方面发挥着重要作用,因此ROV的研究和广泛应用对于国民经济的发展具有重要的现实意义。而拥有稳定、可靠的ROV姿态是其进行水下作业的重要保障[1]。在水下作业时,ROV上的机械手伸展过程中会引起系统重心位置发生变化,导致载体发生纵横倾运动,影响作业效率,因此研究机械手运动引起ROV姿态的稳定技术具有重要的实际意义和实用价值[2]。当前国内外对ROV的姿态控制主要有两种形式,分别是推进器控制姿态和重浮心相对位置控制姿态[3-5]。无论采用哪种形式,工程技术人员都会采用计算机技术进行研究分析,缩短研究时间、降低研究成本。
哈尔滨工程大学的杨超等[6]提出了一种水下机器人模糊双闭环PID方法,通过计算机技术进行仿真分析,确定了所提方法的有效性和可行性。周焕银等[7]提出将神经网络动态滑模面控制方法应用到ROV运动之中,通过MATLAB仿真平台和半物理仿真平台,验证了所提方法的鲁棒性和抗干扰性。文中将所研究的对象和方法结合起来,通过MATLAB技术进行分析,以验证所提的方法的有效性及其控制效果。
1 作业型水下机器人姿态建模
为了方便描述ROV的运动特性,确定其在水下的姿态、速度、方位,有必要建立ROV的坐标系。根据国际水池会议推荐的和造船与轮机工程学会术语公报推荐的体系,建立两个空间直角坐标系[8]。一个是惯性坐标系E-ξηζ,另一个是载体坐标系O-xyz。具体如图1所示。
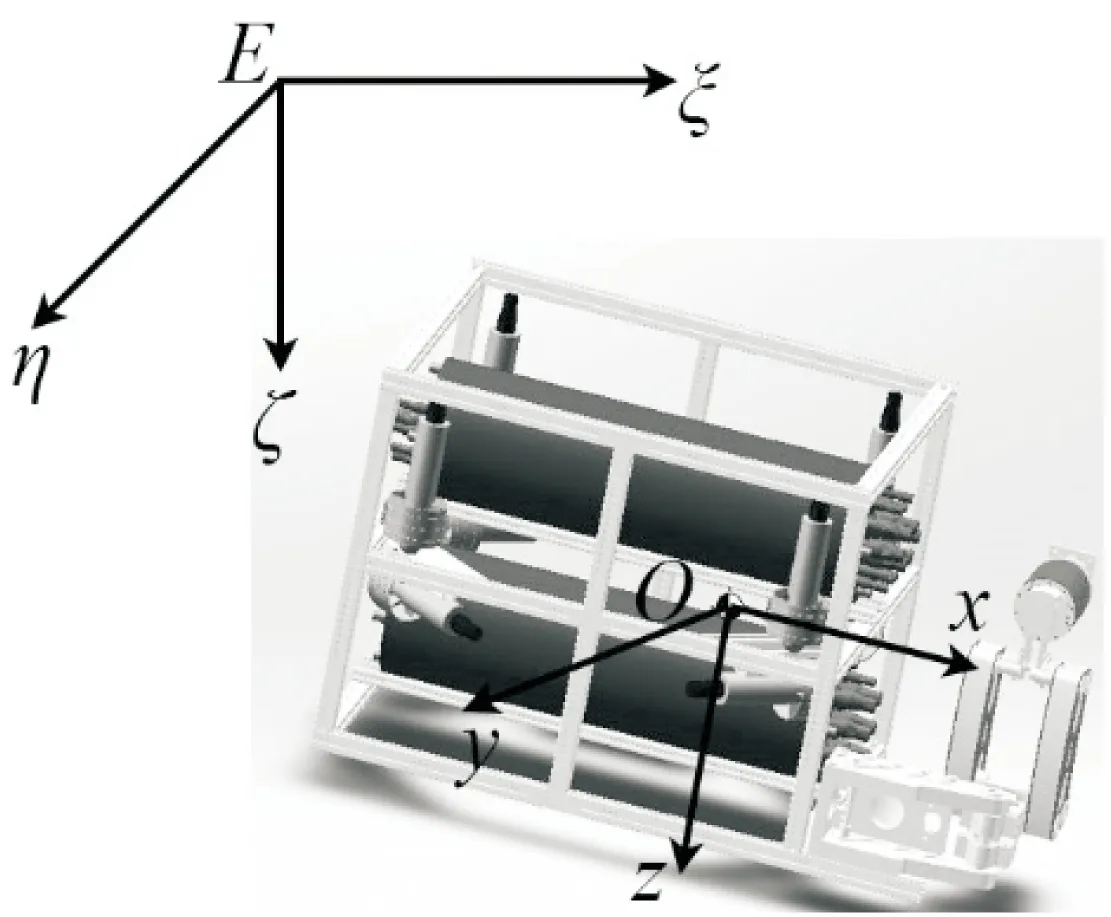
图1 水下机器人坐标系
在惯性坐标系中,水下机器人的位置和方向可以描述为[xyzφθψ]。其中x、y、z分别为ROV在惯性坐标系中的位置;φ、θ、ψ分别为ROV对惯性坐标系的横倾角、纵倾角、航向角。
在载体坐标系,ROV的线速度、角速度可以描述为速度矢量V=[uvwpqr]。其中u、v、w是ROV线速度矢量在载体坐标系中的3个分量,分别为横向移动速度、纵向移动速度和垂向移动速度;p、q、r是ROV角速度矢量在载体坐标系中的3个分量,分别为横倾角速度、纵倾角速度和偏航角速度。
由于ROV在操作过程中会改变系统的重心,为了保证其能够快速、顺利地完成水下任务,有必要对ROV载体姿态进行平衡控制。由于作业过程中ROV在载体坐标系内会发生较为明显的纵倾运动,影响水下作业效率。为了解决该问题,需要调节控制ROV的纵倾和横倾姿态,所以建立机器人载体的纵倾和横倾姿态运动方程。根据文献[9],经过修改和简化,得到ROV载体的纵倾姿态运动方程与横倾姿态运动方程。
纵倾姿态运动方程为:
(1)
横倾姿态运动方程为:
(2)
2 模糊滑模控制器的设计
由于滑动模态具有灵活的设计性,且不受被控对象的参数变化和外干扰,因此滑模变结构控制系统的鲁棒性比一般常规的控制系统要强,且设计方法相对简单。但是由于滑模变结构控制会产生抖振问题,因此需要与其他的控制方式相结合来削弱其抖振的影响[10]。模糊控制是根据经验,以降低抖振来设计模糊逻辑规则,或采用模糊逻辑实现滑模控制参数自调整,可有效降低滑模控制抖振。模糊滑模控制策略包含了上述算法优异功能,对于系统的控制能力更强。
2.1 滑模控制器设计
滑模变结构控制系统设计可分成两步[11-12]:
(1)设计切换函数s(x)。切换函数的设计不仅需要保证滑模运动的渐进稳定,而且其应具有良好的动品质;
(2)系统滑模运动的到达条件由滑模控制律来满足,因此所设计的控制律应能在切换函数上形成滑动模区。
考虑非线性系统[10,13]:

(3)
其中,f和g为未知非线性函数,g>0,u(t)为系统的控制输入信号,θ(t)为系统的输出信号,d(t)为外界干扰信号,
定义跟踪误差:
e(t)=θ(t)-θd(t)
(4)
其中,θd(t)为期望位置。
定义积分滑模面为:
(5)
其中,k1和k2为非零正常数。
(6)
通过确定k1和k2,跟踪误差e(t)及其导数趋近于零。
假设f、g、d(t)已知,那么可以求出理想控制器为:
(7)
由于滑模控制的不连续性开关特性会引起系统的抖振现象,为此引入模糊控制理论,以此来减弱抖振现象,提高滑模控制器的鲁棒性。
2.2 模糊滑模控制器设计
由式(3)可知,f、g、d(t)均是未知函数,因此u*(t)无法用线性函数表示,为此采用模糊系统来趋近u*(t)。取变量αi,对其进行模糊化处理,设定模糊控制器的新输出函数,即系统的控制输入函数:
ufz(s,α)=αTξ
(8)
其中,α=[α1,α2,…,αm]T,ξ=[ξ1,ξ2,…,ξm]T。
定义ξ为:
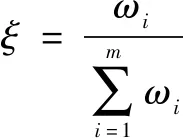
(9)
其中,ωi为第i条规则权值。
(10)
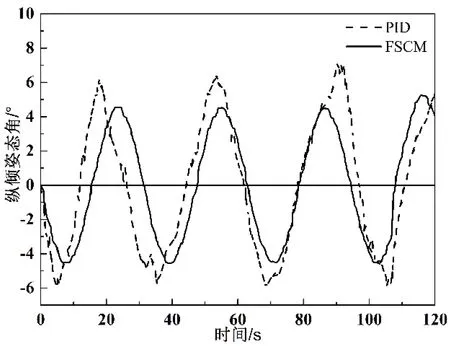
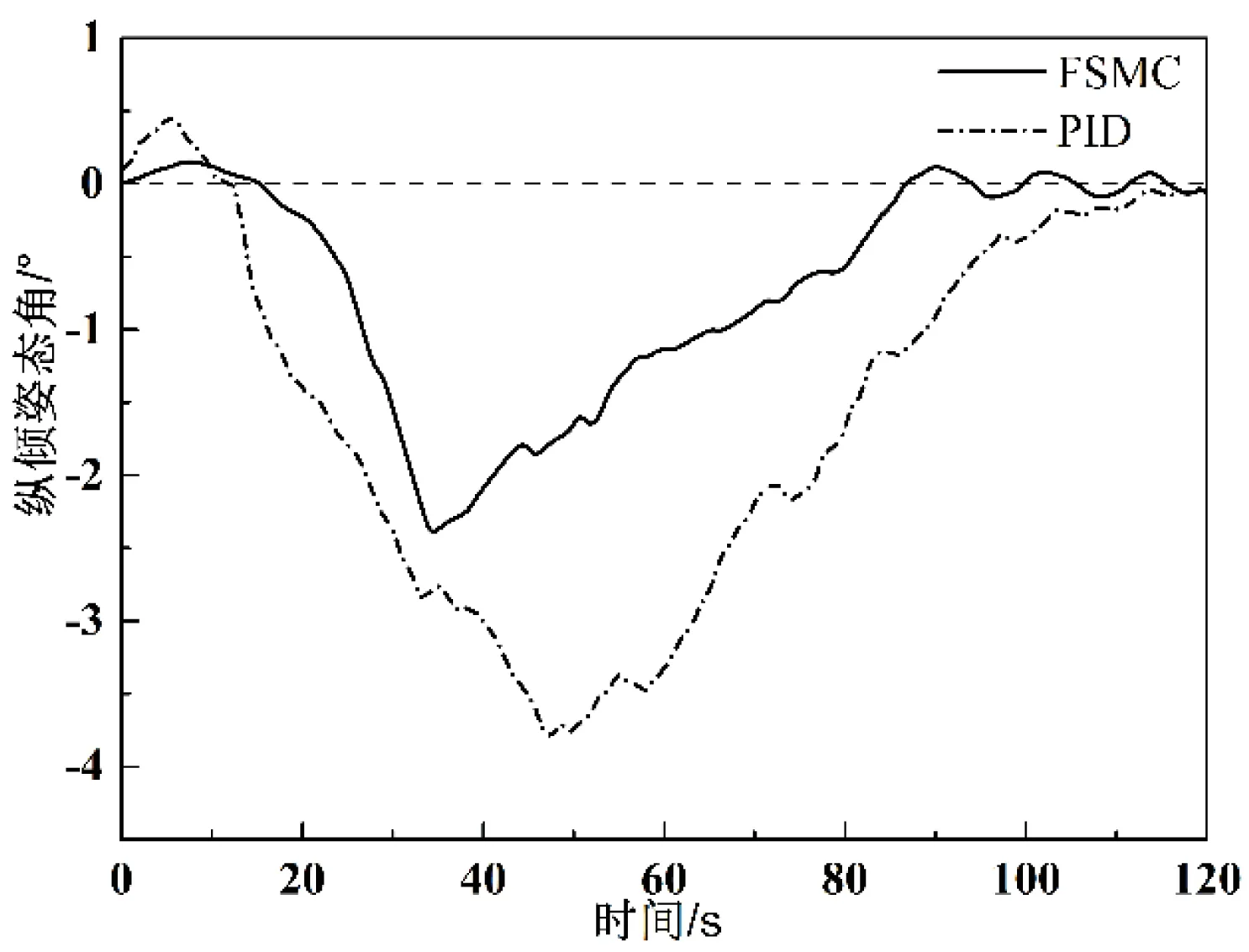
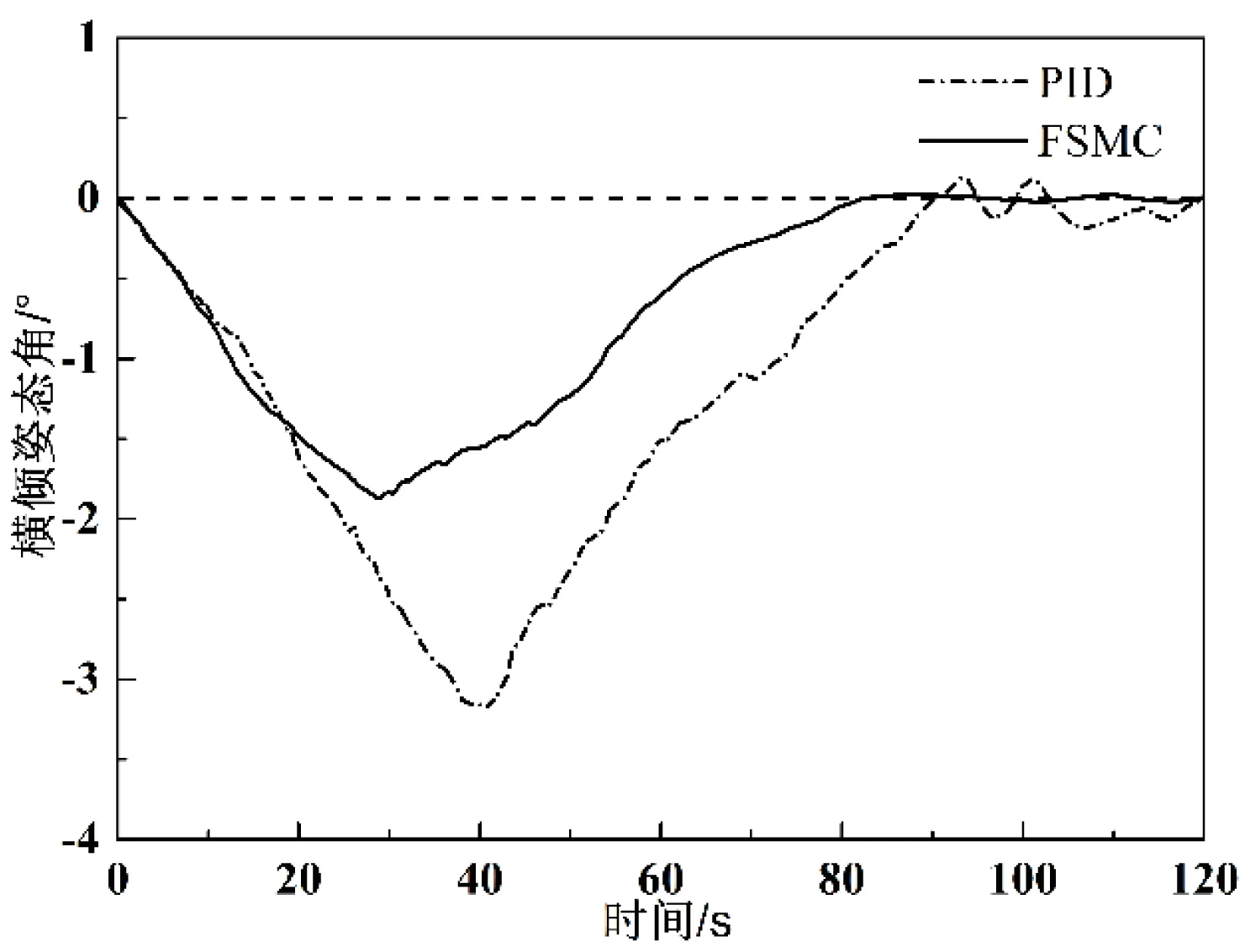
其中,ε为实际近似误差,且满足|ε| (11) 控制函数采用以下形式: (12) 由式(10)定义: (13) (14) 因此可得: (15) 进一步可得: (16) 由式(12)和式(16)可得: g(θ,t)[ufz+uvs-u*(t)] (17) (18) 其中,β为非零常数。 对上式求导,可得: (19) (20) 其中,sgn(·)为符号函数。 则式(19)可变为: (21) 根据以上分析,模糊控制器是首先对滑模面轨迹函数s(t)进行了模糊化处理,削弱抖振现象的影响,然后在模糊控制变量输入时采用满足李雅普诺夫理论定律,确定了系统运动的边界范围,实现了模糊控制。 前一节设计了模糊滑模控制器(Fuzzy sliding mode control,FSMC),本节将其与常规PID控制器进行仿真对比,验证所设计的模糊滑模控制器在ROV载体姿态控制中的控制效果[14-15]。首先以机械手关节正弦运动为对象进行仿真,然后再模拟ROV悬停作业,即ROV自身位置固定不动,其上的机械手做伸展运动,进行仿真分析。 由图2分析可知,在常规PID控制下ROV纵倾姿态角均方差为3.77°,而FSMC控制下纵倾姿态角均方差为2.98°,其值下降了20.95%。它们的最大绝对值和平均绝对值分别是7.05°、5.27°和3.30°、2.63°,分别下降了25.25%和20.30%。同时从图2可以看出,FSMC控制下纵倾姿态角比常规PID控制明显收窄。由图3分析可知,FSMC相比常规PID控制,纵倾姿态角度误差的均方差、平均绝对误差、最大绝对误差分别下降了29.69%、12.5%、8.44%。以上数据表明,文中设计的FSMC在机械手运动过程中对纵倾姿态的控制效果优于常规PID控制。 图2 纵倾运动角度曲线 图3 角度误差 由图4分析可知,在常规PID控制下ROV横倾姿态角均方差为2.87°,而FSMC控制下纵倾姿态角均方差为2.21°,其值下降了23.00%。它们的平均绝对值分别是2.55°和1.96°,下降了23.14%;它们的最大绝对值分别是4.87°和3.67°,下降了24.64%,同时由图4可以看出FSMC控制下横倾姿态角比常规PID控制收窄。由图5分析可知,FSMC相比常规PID控制,纵倾姿态角度误差的均方差、平均绝对误差、最大绝对误差分别下降了39.68%、38.60%、42.50%。以上数据表明,文中设计的FSMC在机械手运动过程中对横倾姿态的控制效果优于常规PID控制。 图4 横倾姿态角度曲线 由图6的仿真结果可知,随着时间的变化,纵倾姿态角由正变负,基本规律是先增大后减小,最后趋近于0度附近。在常规PID控制条件下,ROV载体发生纵倾姿态角在6 s时最大,最大值为0.52°,在约45 s时达到最大负角,该值为-3.80°,之后姿态角开始慢慢恢复到0°,于115 s到达0°附近。在FSMC条件下,ROV载体发生纵倾姿态角在7 s时最大,最大值为0.14°,在34 s时达到最大负角,该值为-2.42°,于90 s到达0°附近,之后开始震荡。FSMC与常规PID相比,最大绝对值减小了36.32%。 图6 倾姿态角度曲线 由图7的仿真结果可知,横倾姿态角是先增大后减小,最后趋近于0度附近。在PID控制条件下,ROV载体发生横倾姿态角在39 s时达到最大,最大值为-3.19°,之后姿态角开始慢慢恢复到0°,于92 s到达0°附近。在FSMC条件下,ROV载体发生横倾姿态角在34 s时达到最大,最大值为-1.88°,于82 s到达0°附近,之后开始震荡。FSMC与常规PID相比,最大绝对值减小了41.07%。 图7 横倾姿态角度曲线 针对水下机械手伸展过程中引起ROV动力学模型中变量与参数的不确定性,以及水下环境的干扰等对ROV载体姿态产生不利影响,提出基于模糊滑模控制的姿态控制方法。通过模糊化逼近模型中不确定性和干扰,用李雅普诺夫稳定性理论确定了系统运动的边界范围,实现了模糊控制。 利用计算机强大的运算能力和MATLAB强大的计算能力,将ROV姿态运动方程与常规PID控制和FSMC分别结合起来进行仿真分析。在机械手关节正弦运动仿真中,模糊滑模控制下载体姿态角度曲线相比于常规PID控制都下降20%以上,且角度误差也有了较为明显的下降。在悬停作业仿真中,模糊滑模控制下载体姿态角度曲线下降的更为明显。通过两种不同方式的仿真,结果表明模糊滑模控制器的控制效果要优于常规PID控制,能够取得良好的控制效果。同时利用计算机技术缩短了研究时间,提高了研究效率。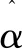


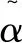
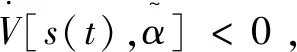
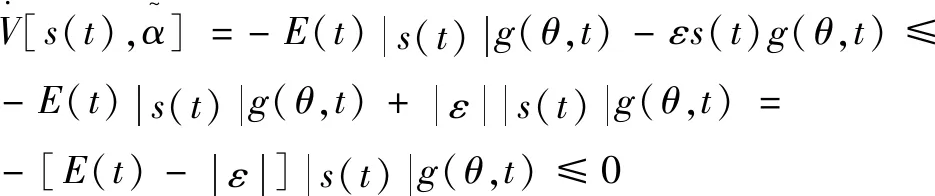
3 仿真分析
3.1 机械手关节正弦运动仿真分析


3.2 ROV悬停作业仿真分析
4 结束语
