引入TBDMS基团提高THAM在超临界二氧化碳中的溶解度

2020-04-07符纯美刘义成晏丽吴鹏闫新豪

当代化工 2020年3期

符纯美刘义成晏丽吴鹏闫新豪

摘要：一种新型亲二氧化碳三羟基甲胺（THAM）衍生物设计并合成得到，测试了其313、323、333 K时在超临界二氧化碳中的溶解行为，TBDMS基团的引入有效增加了化合物的二氧化碳溶解性。将实验测定的溶解度数据与Chrastil、KJ、SS、MST、JCF五种不同的热力学理论半经验模型进行了关联，理论值和实验值具有良好的一致性。通过比较五种热力学模型得到Chrastil模型的相关度最好，平均绝对偏差（AARD%）最低为（0.52～2.86）%。此外，还根据Kumar和Johnston理论计算了化合物在超临界相的偏摩尔体积。

关键词：亲二氧化碳;三羟甲基甲胺;叔丁基二甲基硅烷基;超临界二氧化碳

中图分类号：TQ013.1 文献标识码： A 文章编号： 1671-0460（2020）03-0564-06

Enhancing the Solubility of THAM by Introducing

TBDMS Group in Supercritical Carbon Dioxide

FU Chun-mei， LIU Yi-cheng， YAN Li， WU Peng， YAN Xin-hao^*

（Hanzhong Vocational and Technical College， Shaanxi Hanzhong 723000， China）

Abstract： A novel CO₂-philic tris-（tert-butyldimethylsilyloxymethyl）aminnomethane was designed and synthesized， and then its solubilities in supercritical carbon dioxide were measured at different temperatures （313， 323， 333 K） in the pressure range of 7.8～9.7 MPa. The measured solubility data were correlated with five different theoretical semi-empirical models （Chrastil， KJ， SS， MST， JCF）， and satisfactory agreements were obtained. The comparison results showed that the Chrastil model had the best relevance， and the lowest average absolute relative deviation （AARD%） varied from 0.52% to 2.86%. Furthermore， the partial molar volume of compound in the supercritical phase was also calculated according to the Kumar and Johnston theory.

Key words： CO₂-philic; THAM; TBDMS; supercritical carbon dioxide

近年来，超临界流体技术在学术界和工业界得到了迅速发展。超临界二氧化碳（scCO₂）是一种清洁介质，已取代传统的有机溶剂用于各种工业目的，因其无毒、廉价、环境友好，且容易获得临界常数（T_C=304.2 K，P_C=7.38 MPa）^[¹^]。由于scCO₂具有良好的传质性能、易回收利用、不产生二次废物等优点，被广泛用作重金属污染物的萃取剂^[2]。尽管scCO₂已成功地應用于有机物的工业分离，但由于电荷要求和弱的溶质-溶剂相互作用，用纯scCO₂直接萃取金属离子的效率很低^[³^]。解决这一问题的方法是添加一种可溶解于CO₂的有机螯合剂，该螯合剂可产生一种金属络合物，该金属络合物可容易地从样品基质中提取到scCO₂中。因此，设计合成高CO₂溶性螯合物配体对高效提取具有特殊意义^[4-6]。

溶质在不同压力和温度的超临界流体中溶解度是应用任何超临界流体所必需的重要参数之一。化合物的溶解度信息对于有效设计和建立模型在超临界分离过程都具有重要意义。一般来说，化合物在介质中的溶解度取决于其分子结构，特别是摩尔质量和端基结构。因此，通过修饰端基，设计合成高亲和CO₂可溶物，将大大有利于CO₂作为溶剂的潜在应用^[²^，⁷^]。基于经济发展和环境保护的要求，人们提出了使用非氟化合物作为二氧化碳亲和基团。含氟化合物造价昂贵且毒性大。因此，设计和合成新的非氟亲CO₂化合物成为一个有趣的挑战^[⁸^，9^]。

三羥甲基氨基甲烷（THAM）已广泛用于对过渡金属离子的络合。为提高其在scCO₂中的溶解度，用叔丁基二甲基硅醚对THAM进行了官能化，并观察到改性THAM在CO₂介质中的高分散性。测定了在（313～333）K温度下，在（7.8～9.7）MPa压力范围内，新的亲CO₂三（叔丁基二甲基硅氧基甲基）氨基甲烷在scCO₂中的溶解度，并用五种不同的热力学半经验模型（Chrastil，KJ，SS，MST，以及JCF模型）。溶解度数据有助于预测该化合物在实验条件外较高压力和温度下的相行为。此外，根据Kumar和Johnston的理论，这些数据将作为优化scCO₂中金属萃取操作条件的指导，并用于估算化合物在scCO₂中的偏摩尔体积^[9]。

1 实验部分

1.1 化学试剂

纯二氧化碳（99.99%）购自韩国空气技术公司。其他的化合物购自Aldrich Chemicals试剂公司，使用时没有经过进一步的纯化。三（叔丁基二甲基硅氧基甲基）氨基甲烷是由三（羟甲基）氨基甲烷制备的，纯度满足后续超临界二氧化碳溶解度测试实验（核磁共振波谱测定纯度超过99%）。

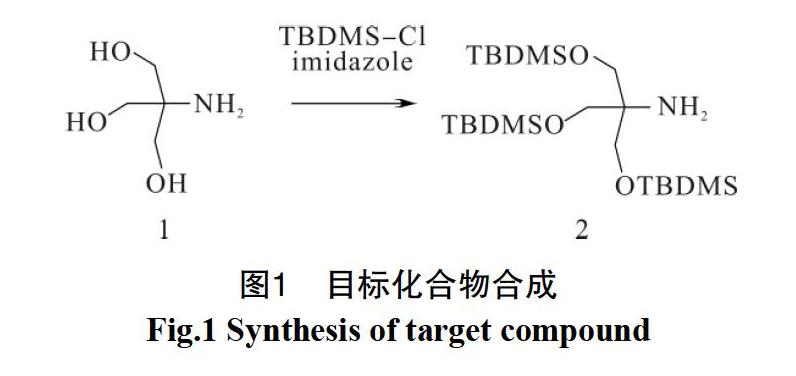
1.2 目标化合物合成

化合物合成方案如图1所示的合成。

将叔丁基二甲基氯硅烷（2.6 g，17.4 mmol）和咪唑（1.2 g，17.4 mmol）溶解于DMF（5 mL）中。加入三羟甲基甲胺（0.6 g，5.0 mmol），在室温下搅拌1 h，用H₂O洗涤，DCM萃取，无水硫酸镁干燥，过滤。减压下除去溶剂，得到白色固体（2.2 g，4.8 mmol，97%）¹HNMR （CDCl₃）δ： 3.4 （s， 6H）， 0.85 （s， 27H）， 0.0（s， 18H）. ¹³C NMR（CDCl₃）δ： 64.0， 57.3， 25.8， 18.2. LRMS （ES⁺）m/z 464.3 [100，（M+H⁺）]。

1.3 超临界CO₂溶解度试验方法

采用两个蓝宝石窗口（V_min=10 mL，V_max=20 mL，0.2 mL/转;Hanwoul Eng.，Korea）的可变体积观察池，连续测定各萃取剂在高压介质中的溶解度点。使用微量吸管或称重纸将化合物放入试管中，并将试管密封。在加热到所需温度后，由注射器泵（260D，ISCO，美国）从液体二氧化碳瓶（99.95%纯度，Air Tech，韩国）中引入二氧化碳。当在固定压力下观察到单相时，缓慢地降低压力，直到在固定温度下出现两相。溶点可以通过两侧的蓝宝石窗目测确定（图2）。

2 结果与讨论

2.1 溶解度结果

目标化合物超临界CO₂中实验溶解度及拟合溶解度、温度T、密度P、压力P和摩尔分数x 5种不同理论半经验模型对溶解度数据的关联结果见表1。

2.2 热力学公式拟合

2.2.1 Chrastil模型

Chrastil模型是最常用的基于密度的模型之

一^[¹⁰^]，它将溶质在scCO₂中的溶解度（S/（g·L^-1））、scCO₂的密度ρ/（kg·m^-3）和温度（T/K）作为方程（1）联系起来：

（1）

其中：A₁～A₃—可调参数，可根据scCO₂中的实验溶解度数据推导。

Chrastil假设在理想情况下，溶质X的一个分子与气体Y的A₁分子结合形成溶剂化络合物XY_A₁的一个分子，并与系统X + A₁Y ? XY_A₁平衡。因此，A₁是一个关联参数，表示溶剂化化合物中scCO₂分子的数量，与溶质的总焓ΔH_total（Δ_solH和_subH）之比，定义为ΔH_total/R，其中R是气体常数，A₃是溶质和scCO₂摩尔质量的函数，定义为ln（M₂+A₁M₁）qA₁lnM₁，其中q是常数。

本文将Chrastil模型中的S/{（g·（L^-1solute）·（mol scCO₂）^-1}转化为（溶质摩尔分数溶解度），重新定义了模型的参数，以便于比较。S可由式（2）计算：

（2）

其中—溶質的摩尔分数;

M₁和M₂—分别是CO₂和溶质的摩尔质量， g·mol^-1。

实验数据与Chrastil模型计算值之间的平均绝对相对偏差（AARD%）可用下列公式（3）计算：

（3）

其中：n—实验数据点的测试次数;

x_i_，_cal和x_i_，exp—分别是溶质摩尔分数溶解度的计算和实验值。

使用Chrastil模型的溶解度数据关联结果如表2所示。图3展示了相关结果的对比图。AARD值为0.52%。

2.2.2 KJ模型

Kumar和Johnston认为在和之间以及在某些情况下在和之间呈现线性关系，依赖于系统且两者都不能有效地推广^[¹¹^]。

与式（1）类似，和之间的线性表达式可以表示为式（4）：

（4）

其中：B₁、 B₂、B₃—可調参数，其中参数B₁与Chrastil模型的参数

A₁相同，定义为ΔH_total/R。

Chrastil模型不同温度㏑S对㏑ρ作图见图4。

使用kJ模型的溶解度数据关联结果如表2所示。图5为对作图。AARD值为1.92%。

2.2.3 SS模型

Sung和Shim讨论了温度对溶解度的影响^[12]。SS模型表明，在对数曲线图中，溶解度等温线是线性的，而它们的斜率随着温度的升高而减小。因此，通过将温度效应考虑在内，对kJ模型进行了修改，如式（5）：

（5）

其中：C₁–C₄—可调参数。

使用SS模型的溶解度数据关联结果如表2所示。图6对作图。AARD值为1.45%。

2.2.4 MST模型

Mendez Santiago和Teja提出了一个基于密度的模型，该模型和之间的线性关系，依据稀溶液理论^[13]：

（6）

其中：D —增强因子;

， —定义为升华压力;

x —溶质的摩尔分数;

P —实验压力。

为了预先确定，可以用Clausius–Clapeyron类型的表达式替换该值。因此，模型可以修改为方程（7）：

（7）

其中：D₁-D₃—可变参数。

MST模型的溶解度数据关联结果如表2所示。图7显示了作为相关结果的对比图。AARD值为2.86%。

2.2.5 JCF模型

由于等温条件下压力与温度之间呈非线性关系，等压条件下压力与温度之间呈非线性关系但在一定范围内压力与温度之间的线性关系，Jouyban等。

提出了另一个基于密度的模型，可以写成公式（8）^[^14]：

（8）

其中：E₁–E₆—可调参数，使用JCF模型的溶解度数据关联结果如表2

所示。AARD值为2.19%。

2.3 溶质偏摩尔体积的估算

溶质的偏摩尔体积是评价溶质在超临界流体中中溶解度的重要参数。所以，计算目标化合物的偏摩尔体积是很有意义的。计算结果可根据Kumar和Johnston理论得出^[¹⁵^]：

（9）

式中：x —溶质的摩尔分数;

和 —分别为溶质的蒸汽压和摩尔体积;

R —气体常数（8.314 J·K^-1·mol^-1）;

—SCF相溶質的偏摩尔体积;

—等温压缩常数;

—相的还原密度;

T —工作温度。

由于的值远大于，的值，所以方程（9）中的第三项可以看作常数，因此，方程（9）可以导出并简化为：

（10）

表3对所得结果进行了概括。如表3所示，溶质的偏摩尔体积随温度的升高而减小。利用Kumar和Johnston的理论估算了目标化合物在溶剂临界点附近的偏摩尔体积，实验上难以测定的。

不同温度关于作图见图8。

3 結束语

设计合成了新的亲CO₂三（叔丁基二甲基硅氧基甲基）氨基甲烷。然后在三个热力学温度下，测定了化合物在scCO₂中的溶解度。化合物在等温条件下的溶解度随压力的升高而增加，而在等压条件下的溶解度随温度的升高而降低。三（叔丁基二甲基硅氧基甲基）氨基甲烷的实验溶解度值与五种不同的理论半经验模型（Chrastil、kJ、SS、MST和JCF模型）模拟相关性，每个模型都得到了很好的一致性。Chrastil模型给出了最佳的相关性拟合。此外，利用Kumar和Johnston的理论计算了化合物在scCO₂中的偏摩尔体积。这项工作可能为设计和合成新的低成本、非氟的亲CO₂化合物提供基础信息。

参考文献：

[1]胡金花，闫俊，李红，彭建钧，等.分散红11在超临界二氧化碳中的溶解度及其模型拟合[J].纺织学报，2019，40（08）：80-84.

[2]李慧，韩兵，常宏宏，乔岩.亲二氧化碳化合物的研究进展[J].化学试剂，2016，38（01）：27-33.

[3]闫新豪，王丹.水杨酸在超临界二氧化碳中络合萃取汞离子[J].当代化工，2016，45（03）：453-455+459.

[4]宋小兰，王毅，宋丹，等.废旧B炸药组分在超临界二氧化碳中的溶解性及其分离工艺[J].火炸药学报，2013，36（06）：20-23.

[5] 刘畅，臧晓南，刘柱，等.二氧化碳超临界流体萃取在裂殖壶菌DHA提取中的应用[J].海洋湖沼通报，2019（05）：135-142.

[6]薛菲，王健，郭凯蕾.超临界CO₂流体萃取技术的应用研究[J].化工管理，2019（11）：114-115.

[7]刘迪，宋晓宇，李婧，尚华，杨建民.超临界二氧化碳萃取核桃青皮多酚及其体内抗氧化性[J].食品工业，2019，40（05）：144-148.

[8]C. Erkey.Supercritical carbon dioxide extraction of metals from aqueous solutions： a review[J].The Journal of Supercritical Fluids， 2000，17： 259-287.

[9]K. Laintz， J.J. Yu， C. Wai. Separation of metal ions with sodium bis （trifluoroethyl） dithiocarbamate chelation and supercritical fluid chromatography [J]. Analytical Chemistry， 1992，64 ： 311-315.

[10]J. Chrastil. Solubility of solids and liquids in supercritical gases [J]. The Journal of Physical Chemistry， 1982， 86：3016-3021.

[11]S.K. Kumar， K.P. Johnston， Modelling the solubility of solids in supercritical fluids with density as the independent variable[J]. The Journal of Supercritical Fluids， 1988，1：15-22.

[12]H.-D. Sung， J.-J. Shim. Solubility of CI disperse red 60 and CI disperse blue 60 in supercritical carbon dioxide[J]. Journal of Chemical & Engineering Data， 1999，44：985-989.

[13]J. Méndez-Santiago， A.S. Teja.The solubility of solids in supercritical fluids[J]. Fluid Phase Equilibria， 1999，158：501-510.

[14] A. Jouyban， H.-K. Chan， N.R. Foster. Mathematical representation of solute solubility in supercritical carbon dioxide using empirical expressions[J]. The Journal of supercritical fluids，2002， 24：19-35.

[15]Z. Yang， H.-J. Yang， J. Tian， C.-Y. Guo， H. Kim. High Solubility and Partial Molar Volume of 2，2′-Oxybis （N，N-bis （2-methoxyethyl） acetamide） in Supercritical Carbon Dioxide[J]. Journal of Chemical & Engineering Data，2011， 56：1191-1196.