基于改进k-means算法的数字图像聚类

高 西， 胡子牧

(重庆医科大学 附属大学城医院，重庆 401331)

1 引 言

随着互联网、5G等技术的飞速进步，可收集的图片数据种类、数量越来越多，数据特征的维度也越来越高。为了从海量图片中快速检索、分类有用的图片，许多研究者将聚类方法用于该领域[1-5]。聚类是模式识别和数据挖掘中的一个重要方向，是一类无监督学习算法，它遵循相似规则将数据样本划分为不同的类，在同一类中的对象之间相似性较高，而在不同类中对象之间相似性较低。到目前为止，很多研究者提出了一些有效的聚类方法，例如k-means[6]、FCM[7]、SOM聚类[8]、AP算法[9]、谱聚类算法[10-13]。其中k-means算法以其对大型数据集的高处理效率而得到了最为广泛的应用。该算法的优点有很多，缺点主要在于：第一，只考虑类内距离，未考虑类间距离；第二，对包含海量样本的数据集的聚类数目上界的确定主要依靠经验，而人为设置的聚类数目上界往往偏大，导致了算法运行效率被降低。

有鉴于k-means算法的第一个缺陷，黄晓辉等[14]提出了一种类内-类间距离加权的k-means算法，该算法的基本思路是，通过在子空间内最大化类中心与其他类内样本点的距离来融合类内和类间距离进行聚类。黄晓辉等在算法中设计了一个目标函数，然后通过求解目标函数来对算法参数进行迭代更新。在真实数据集上的表现证实了该算法相比于现有k-means类算法的优越性。针对传统k-means算法的第二个缺陷导致的聚类数目上界设置偏大，进而导致算法运行效率偏低的问题，周世兵等[15]通过合理设置AP算法的初始参数确定了聚类数目的上界，该方法比传统的经验估计更为有效，大大提升了k-means算法的执行效率。本文提出了一种改进型的k-means算法，在该算法中，周世兵等提出的最小聚类上界确定方法与黄晓辉等提出的类内-类间距离加权k-means算法被合并使用。本文所提出的方法被用于一个标准聚类图像数据集的聚类中。实验结果显示，本文所提出的改进型k-means相比于传统k-means和另外几种K-means类算法，达到了更高的性能，同时执行效率也大为提升。

2 理 论

2.1 类内-类间距离加权k-means算法

与其他加权k-means 算法类似，类内-类间距离加权k-means算法也包含3个计算步骤：更新分配矩阵U、更新类中心矩阵Z和更新特征权重矩阵W。

设有一包含n个m维样本的数据集X={X1,X2,…,Xn}。数据对象分配矩阵U∈Rnk为一个只包含0和1的矩阵。Z={Z1,Z2,…,Zk}为类中心矩阵，其中Zp={zp1,zp2,…,zpm}为第p个类中心。W={W1,W2,…,Wk}为权重向量，其中Wp={wp1,wp2,…,wpm}代表第p个类的特征权重，wpj为第p类中第j个特征的权重。该算法的目标函数如公式(1)所示。

，

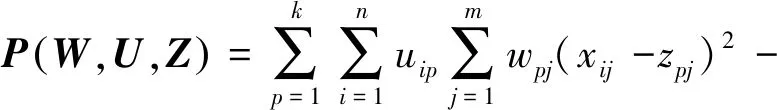
(1)

其中：η是类内-类间距离调整参数，γ是权重分布控制参数。

固定权重矩阵W和类中性能矩阵Z，式(1)在满足式(2)时可以最小化。

，

(2)

固定数据对象分配矩阵U和特征权重矩阵W，P(W,U,Z)可以最小化当且仅当:

，

(3)

固定数据对象分配矩阵U和类中心矩阵Z，P(W,U,Z)可以最小化当且仅当：

,(4)

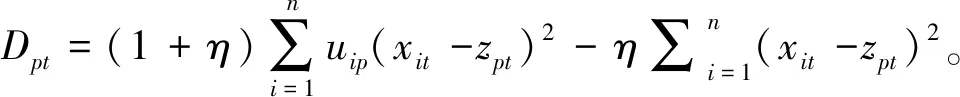
类内-类间距离加权k-means算法的运行流程如下：

步骤1：输入数据集X，类数目k，参数η和γ；

步骤2：随机初始化类中心Z和特征权重W；

步骤3：固定W和Z，由式(2)求解U；

步骤4：固定W和U，由式(3)求解Z；

步骤5：固定U和Z，由式(4)求解W；

步骤6：重复步骤3～5直到目标函数(1)收敛或U不再改变。

2.2 基于近邻传播聚类算法的类数量上界确定方法

在运用k-means算法时，一般难以直接确定数据集的最佳聚类数目，因此一般的做法是根据经验确定聚类数目上限，在该数目上限之内，依次按照逐渐增大的聚类数目进行k-means聚类。由于经验估计往往导致聚类数目上限偏大，因此这种做法在实际应用中效率不高。文献[15]采用近邻传播算法(Affinity Propagation clustering, AP)来确定聚类数目上限，大大提高了效率。其详细的运行步骤如下：

步骤1：将所有AP偏向参数pi(i=1,2,…,n)统一设定为吸引度中值pm，然后通过AP算法确定聚类数目的搜索上界kAP;

步骤2：在聚类数目范围[2,kAP]内依次进行k-means算法，得到每个聚类数目下的聚类结果；

步骤3:按照设定好的评价指标确定最优聚类数目。

3 图像聚类方案设计及实验

3.1 图像聚类方案设计

本文所提出的图像聚类算法的整体流程框图其详细运行流程如下：

步骤1：将待聚类的彩色图片数据集中图片通过双线性插值法进行缩放，缩放后尺寸统一为50×50；

步骤2：将待聚类的彩色图片数据集中已缩放图片的亮度分量逐个进行局部二值模式(Local Binary Pattern, LBP)图生成；

步骤3：将步骤2生成的所有LBP图由二维矩阵按行展开成一个一维行向量，每张LBP图像对应一个行向量。所有的行向量构成图片样本的聚类数据集；

步骤4：将所有AP偏向参数pi(i=1,2,…,n)统一设定为吸引度中值pm，然后通过AP算法确定聚类数目的搜索上界kAP;

步骤5：在聚类数目范围[2,kAP]内依次进行类内-类间距离加权k-means算法，得到每个聚类数目下的聚类结果；

步骤6：按照平均Silhouette指标值确定最优聚类数目；

步骤7：输出最优聚类数目下的聚类结果。

其中平均Silhouette指标值[16]的定义如公式(5)所示。

，

(5)

其中:bi为第i个样本到其他每个类中样本平均距离的最小值，ai为第i个样本与类内所有其他样本的平均距离。

图1 算法整体运行流程

3.2 实验

3.2.1 实验条件

本文中所涉及算法均使用MATLAB R2019a软件平台实现，实验所用计算机配置为：CPU使用AMD Ryzen 5 3600X 4 GHz，内存64 GHz，显卡为NVIDIA GeForce RTX 2070，系统为 Linux Ubuntu系统。

图2 本地图像数据集中部分样本

图3 GHIM10-K图像数据集中部分样本

本文在实验中所使用的图片数据集共计两个。第一个为本地图片数据集，包含4 200张彩色图片，共分为6类：球类、景物类、建筑类、熊猫类、人脸类和汽车类。每类图片均包含700张，每张图片的大小均为320×320。本地图片数据集的部分样本数据如图2所示。第二个图片数据集为GHIM10-K图片数据集。该数据集中包含共计10 000张彩色图片，分为烟花、日落、船、花、建筑、高山和昆虫等20个类，每类包含500张尺寸为300×400的图片。GHIM10-K图片数据集中的部分图片样本如图3所示。

3.2.2 聚类效果评价指标

在实验中，调整兰德系数(Adjusted Rand Index, ARI)、宏F1度量(Marco-F1)和聚类时间用于进行算法聚类效果的评价指标。ARI的计算公式如式(6)所示。

，

(6)

宏F1度量的计算公式如式(7)所示。

，

(7)

其中KMacro-P和KMacro-R分别为宏查准率和宏查全率。这两个指标的计算公式如式(8)所示。

，

(8)

其中KTPi为第i类样本被正确分类的数目，KFPi为其他类样本被错误分类至第i类的数目，KFNi为第i类样本被错误分类至其他类别的数目。

3.2.3 试验结果及分析

将待聚类的彩色图片数据集中图片通过双线性插值法进行缩放，缩放后尺寸统一为50×50，然后将待聚类的彩色图片数据集中已缩放图片的亮度分量逐个进行LBP图生成。部分样本的LBP图如图4所示。

图4 部分图片样本对应的LBP图

将所有的LBP图按行展开成一维行向量，每个向量作为一个样本，所有的样本构成聚类数据集，通过本文所提出的改进型k-means算法所确定的聚类数目搜索上界kAP和经验估计确定的聚类数目搜索上界ke，以及通过平均Silhouette指标值确定的最优聚类数目如表1所示。在范围[2，kAP]内不同聚类数目对应的平均Silhouette指标值变化情况如图5所示。通过表1可以看出，相比于经验估计，AP算法所确定的聚类数目上界更为准确，这将大大减少算法的执行时间，提高算法的执行效率。同时，也可以发现，通过平均Silhouette指标值确定的最优聚类数目达到了实际类数目的最优无偏估计。

为了证实本文所提出的图像聚类算法的优越性，将文献[17-18]中的方法与本文方法进行比较。这3种算法各自将3.2.1小节中介绍的两个图像数据集进行50次聚类，50次实验得到的平均ARI、平均宏F1度量和平均执行时间列于表2。通过表2可以看出，与两种参考算法相比，本文所提出的算法具有更高的执行效率，更具有实用性，这主要是因为本文方法将聚类数目搜索上界缩小所致。同时，相比于两种参考算法，更高的平均宏F1度量也证实了本文所提算法的优异聚类精确度。

表1 两种数据集的聚类数目搜索上界和最优聚类数目

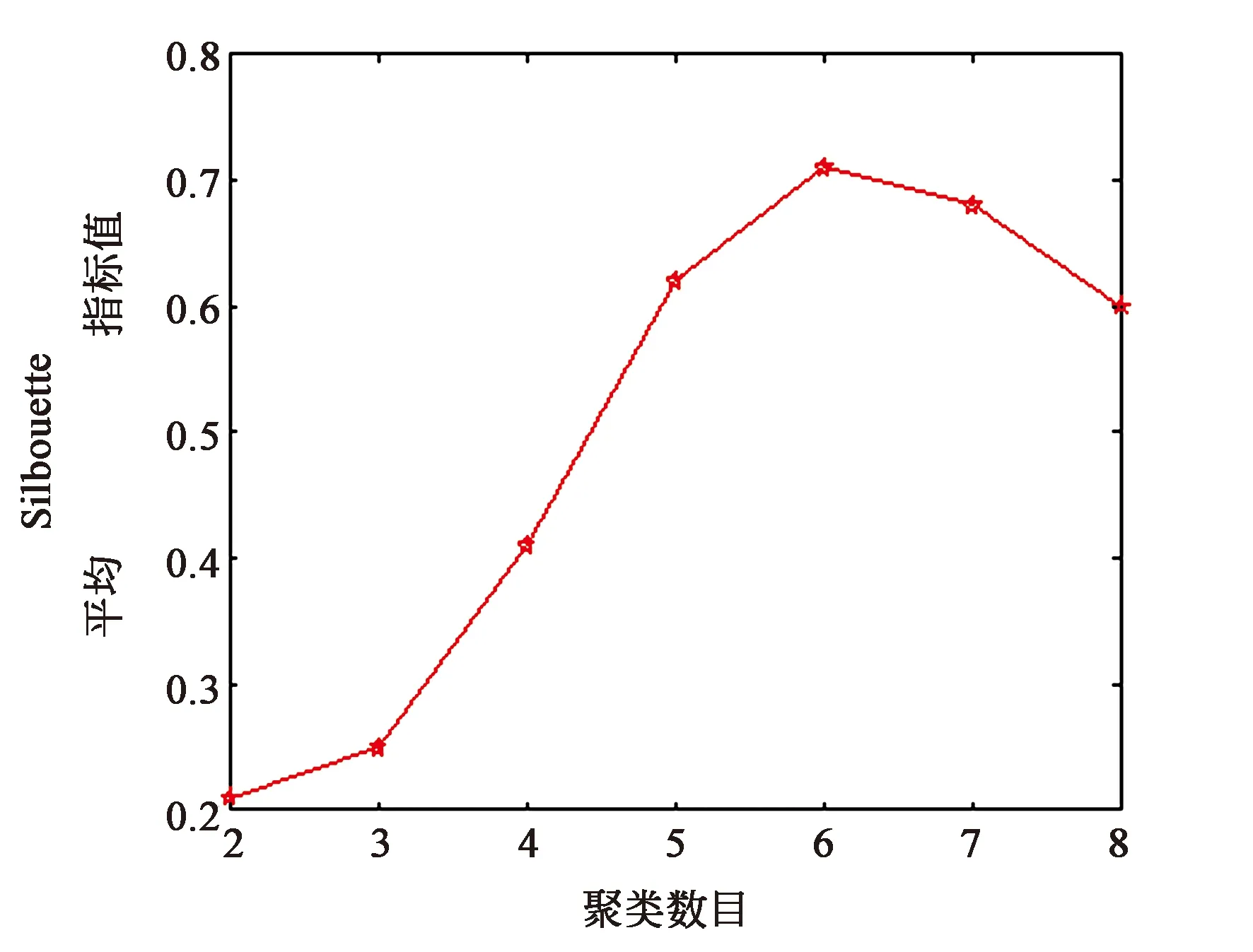
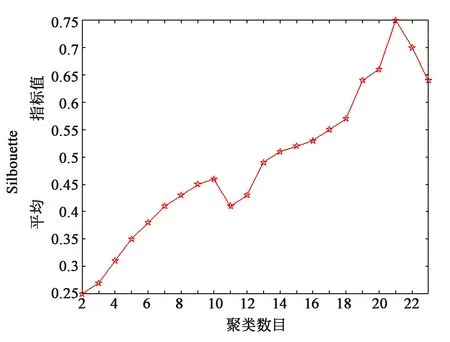
图5 本地数据集(左)和GHIM10-K数据集(右)在范围[2，kAP]内的聚类数目-平均Silhouette值图

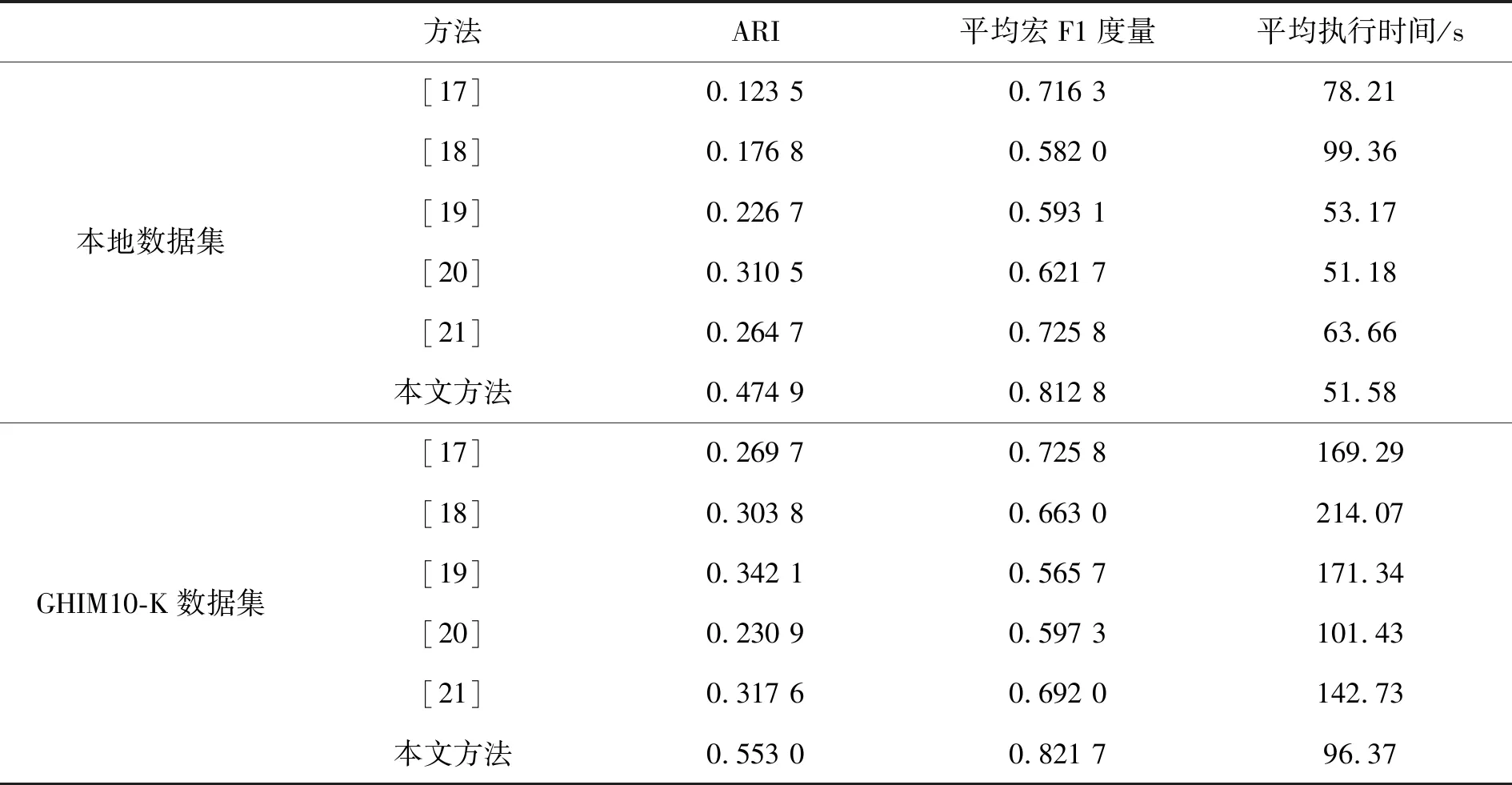
表2 3种算法的比较

4 结 论

针对海量彩色图像高效精确聚类问题, 本文引入了一种改进型k-means算法并将其应用于彩色图像聚类中。该算法由类内-类间距离加权k-means算法和基于近邻传播聚类算法的聚类数量上界确定方法组成。在实验中，彩色图像通过双线性插值缩放，缩放后尺寸统一为50×50。缩放后彩色图像的亮度分量的LBP图被重组成行向量然后构成样本特征数据集，本文所提出的改进型k-means算法被用于对样本集进行聚类处理。实验结果显示，在平均宏F1度量和ARI的测试中，本方法相比于传统方法达到了更高的水平，证实了本文所提方法优异的聚类准确度。同时，由于聚类数目上界的准确确定，相比于传统方法，本方法也更具有执行效率。