轮廓波域内局部对比度增强的彩色图像灰度化算法

王冰雪，刘广文 ，刘 美，陈广秋

(长春理工大学 电子信息工程学院，吉林 长春 130022)

1 引 言

灰度图像因其能够真正反映图像特征，信息量小，系统处理效率高，对传输带宽及存储空间要求较低，在指纹档案管理、运动目标追踪、医学影像检查诊断和艺术美学等领域得到广泛应用[1]。

彩色图像灰度化的本质是一个将三维RGB像素矩阵转换成二维灰度矩阵的过程，其基本思想是将三维彩色图像中的各像素值，根据具体的应用场景选择最佳的映射函数，依次映射到特定的灰度级上，在转换过程中不可避免地会丢失一些结构信息[2]。最简单的灰度化方法是采用固定权重对RGB通道进行加权求和，如MATLAB软件中的rgb2gray函数，或是直接利用某个色彩空间的亮度通道，如HSI 、CIE Lab，这些方法虽然简单易实现，但信息丢失也最为严重。

目前彩色图像灰度化算法主要包括全局映射法[3]和局部映射法[4]两类。全局映射法注重的是彩色图像整体颜色分布差异，对所有像素采用相同的映射函数，能够较好保留全局结构信息，但对局部特征信息的区分度较差。如Gooch 等人[5]利用灰度差与颜色差的最小二乘构造目标函数，采用共轭梯度算法求解以保持颜色对比度。局部映射法注重的是色彩在局部空间的分布差异，根据局部差异调整局部空间的像素强度，能够精确地保留局部特征，但图像的整体结构信息损失严重，不能保证全局颜色信息的一致性。如Smith等人[6]提出了一种基于感知的彩色图像灰度化算法，该算法首先估计相等亮度颜色之间的差异，并通过全局映射和H-K效应确定颜色排序，然后再通过拉普拉斯图像金字塔来实现局部对比度的增强。该算法只强调了相邻域内的对比度，忽略了非相邻区域内的色彩信息，在灰度化图像中容易产生晕轮现象。

自然场景图像中包含了不同尺寸的目标物，形成不同尺度的结构，各尺度目标物的结构排列组成了整体结构信息，局部结构信息包括局部亮度及对比度信息。人眼视觉感知系统是一个多通道多尺度模型，对场景的观察是由全局到局部，自适应地感知各尺度目标物的信息。对于一幅具有适中的整体亮度、良好的局部对比度、清晰的目标结构轮廓和纹理细节信息的图像，人眼具有良好的视觉感受。而彩色图像灰度化的最终目标就是用灰度图像最优地重现彩色图像的表达意图，包括对比度和显著特征信息，同时保持可感知的梯度幅值和方向。因此,为了得到较好的灰度图像，同时兼顾人眼的视觉感受，应该考虑在保持边缘极性、整体亮度和颜色顺序的基础上，将彩色图像中的颜色对比信息尽可能多地映射到灰度图像中，以增加局部对比度，优化人眼的视觉感受和感知的准确性。本文综合全局映射法和局部映射法的优点，提出了一种轮廓波域内局部对比度增强的灰度化算法，采用全局映射法获取能够保留全局结构信息的初步灰度化图像，在轮廓波(Contourlet)变换域内对方向细节图像进行局部增强，有效地保留原始彩色图像的局部对比度信息，最后叠加两幅图像得到最后的灰度化图像。

2 算法基本原理

2.1 轮廓波变换基本原理

轮廓波变换(Contourlet)包括多尺度分解和方向分析两部分，分别由拉普拉斯金字塔和方向滤波器组来实现。拉普拉斯金字塔(Laplacian Pyramid，LP)将图像分解为低频子带和带通子带，低频子带是由原图像经过低通滤波和行列下采样后形成的，经过上采样和低通滤波后形成低频分量，原图像减去此低频分量，得到高频子带。方向滤波器组(Directional Filter Bank，DFB)对高频子带进行方向滤波，得到2d个方向子带(d为正整数)[7]。对低频子带重复上述操作，可实现原始图像的多分辨率多方向的分解。轮廓波变换的原理如图1所示。

轮廓波变换基的支撑区间为长条形结构，利用图像的几何正则性，能用较少的系数来逼近曲线，其最终结果是用类似于轮廓段(Contour Segment)的基结构逼近原图像[8]。

图2所示为512×512的Lena灰度图像和彩色图像分别经过2级轮廓波分解得到的子带，分解方向数分别为4和8。从图2中可以看出，不同方向的子带图像清晰地描述了不同方向的细节信息和轮廓特征。

图2 “日出”图像的初步灰度化结果

由于LP和DFB是完全重构的滤波器，所以轮廓波变换可以实现完全重构。若滤波器是正交的，轮廓波变换提供一个紧支撑框架，对于第j尺度上进行lj级方向分解，轮廓波变换的支撑基大小为Kwidth=C2j，Klength=C2j+lj-2。

2.2 局部对比度增强的彩色图像灰度化算法

基于轮廓波变换的局部对比度增强的彩色图像灰度化算法主要包括两部分：彩色图像的初步灰度化与灰度图像的局部对比度增强。初步灰度化部分是通过预测彩色物体颜色的方法来更多地保留原彩色图像的整体结构信息；局部对比度增强部分是利用轮廓波变换提取彩色图像和初步灰度化图像的多尺度多方向特征信息，根据每个尺度上特征信息色彩的对比度，按比例地将色度信息添加到初步灰度化图像中以实现输出图像的局部对比度增强。其过程主要包括4个步骤：

(1)将彩色图像从RGB色彩空间转换至CIE Lab色彩空间；

(2)在CIE Lab色彩空间求取彩色图像的感知亮度，然后利用色度分量a和b对感知亮度进行修正，得到初步灰度化图像；

(3) 对输入彩色图像和初步灰度化图像进行相同尺度和方向的轮廓波分解；

(4) 计算彩色图像和初步灰度化图像各方向子带间色度对比度的比值，并按比例添加到初步灰度化图像中，得到最终的灰度化图像。

2.2.1 彩色图像的初步灰度化

，

(1)

，

(2)

.

(3)

，

(4)

像素间色差目标函数定义为：

，

(5)

其中：k表示八邻域像素集，δij为像素间距离标量，为了求取x1和x2的值，只需求解下列最优化问题：

.

(6)

采用共轭梯度迭代算法[10]求解式(6)，将x1和x2值带回式(4)，得到对应的初步灰度化图像g。

图3所示为“日出”图像(256×256)的初步灰度化结果。

图3 “日出”图像的初步灰度化结果

从图3可以很明显地看出，初步灰度化图像中保留了图像色彩的大部分对比度信息，解决了部分灰度值的分配问题，并对亮度映射不能区分的颜色进行了适当的排序。

2.2.2 轮廓波变换域的局部对比度增强函数

人类视觉系统对于局部对比度的变化十分敏感，而彩色图像灰度化时由于像素维数的缩减，必然会引起彩色对比度的缺失。为了更好地表达原始彩色图像的局部对比度，需要对初步灰度化图像增强局部对比度。本文在轮廓波变换域内构造对比度增强函数，对初步灰度化图像进行多尺度多方向锐化以提高局部对比度。首先，对彩色图像和初步灰度化图像分别进行轮廓波分解，然后计算彩色图像与初步灰度化图像的对应高频方向子带的色彩对比度比值，作为初步灰度图像各高频方向子带系数的权重，得到增强后的高频方向子带系数，最后利用轮廓波逆变换重构系数，得到增强后的细节图像。最终的灰度图像g**可以利用下列映射函数得到：

g**=g+g*

，

(7)

其中：g为初步灰度化图像，g*为局部对比度增强后的细节图像，定义为：

，

(8)

，

(9)

图4 “日出”图像的最终灰度化结果

从图4中可以看出经过局部对比度增强后得到的灰度图像比图3所示的初步灰度化图像能够更大程度地保留原始图像的细节信息，具有更高的局部对比度和更好的视觉效果。

3 实验结果分析

3.1 不同灰度化算法的主观评价分析

图5 第一组不同灰度化算法实验结果

从图5可以看出，CIE Y算法在细节保留方面表现得很不理想，例如第3幅测试图像中的太阳和第4幅测试图像中红色框中的部分在灰度化之后都没能很好地体现出来，视觉效果很差；Gooch等人算法对于大部分测试图像的灰度化效果较好，但是对第2幅和第6幅测试图像的灰度化效果较差，并不能很好地体现彩色图像的色彩对比度信息；Grundland等人算法同样仅仅只对部分测试图像的灰度化效果较为理想；Smith等人算法的灰度化结果整体表现较差，丢失了图像的很多细节信息和对比度信息；Lu等人算法和本文算法的灰度化结果均表现出了良好的整体结构和局部细节信息，都能很好地保持输入彩色图像的对比度，但在视觉效果方面本文算法的结果更符合人眼视觉感知，感知亮度和局部对比度表现得更理想。为了更直观地说明本文算法的有效性和稳定性，将其余10幅测试图像的灰度化结果示于图6中。

图6 第二组不同灰度化算法实验结果

综合图5和图6的灰度化结果，本文算法在灰度化过程中不仅能够良好地保持原图像的整体结构和体现色差的对比度，且具有良好的整体视觉感知效果。

3.2 不同灰度化算法的客观评价分析

灰度化图像间差异较小时，视觉观察很难做出准确的主观评价，需要采用客观评价方法对灰度化图像进行定量分析。本文客观评价方法采用显著图结构信息相似度(Saliency Map Structural Similarity，SM-SSIM )[15]和E-Score[11]模型两种评价方法。SM-SSIM表征的是彩色图像显著图和灰度图像显著图的结构信息相似程度，其值越大越好；E-Score是颜色对比度保持度(Color Contrast Preserving Ratio, CCPR)与颜色内容保真度(Color Content Fidelity Ratio，CCFR)的调和平均值，其值越大越好。CCPR表征的是灰度图像中对比度与输入颜色的相似程度，其值越大越好；CCFR表征的是灰度图像中结构内容与输入颜色的相似程度，其值越大越好；表1和表2分别列出了本文算法与其他6种算法对所选16幅测试图像灰度化结果的SM-SSIM和E-Score的评价数据。其中E-Score是在阈值τ=10时得的评价数值。表中加粗的数值表示同一测试图像在各种灰度化算法中取得的最大值。

表1 不同灰度化算法实验结果的SM-SSIM评价数据

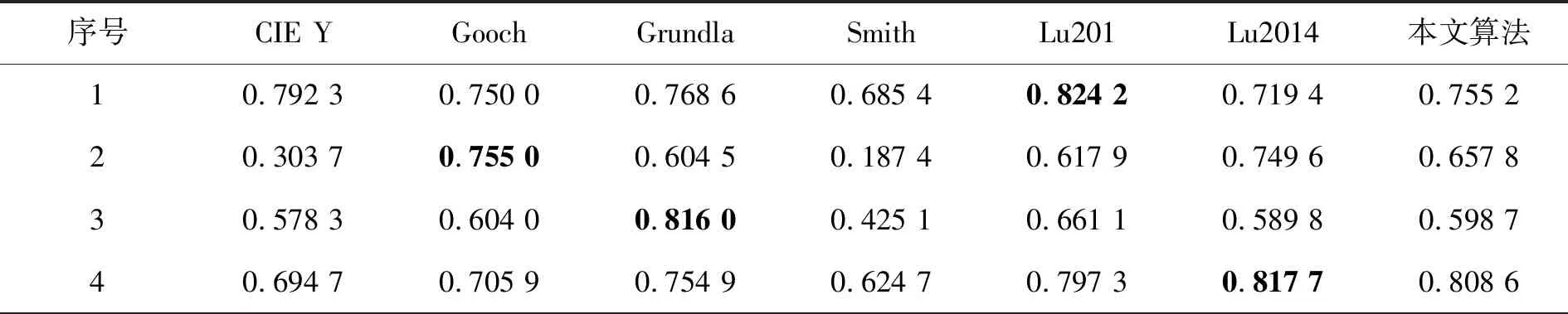
表2 不同灰度化算法实验结果的E-Score评价数据

续 表

从表1和表2中可以看出，SM-SSIM和E-Score的最优评价结果多数都来自本文算法，且结果的平均值均为最优，与主观评价一致，说明本文算法具有一定的优越性和稳定性，能够有效地保持彩色图像的整体结构信息和局部彩色对比度。

图7所示为各灰度化算法的E-Score的平均值随阈值τ变化的曲线图。

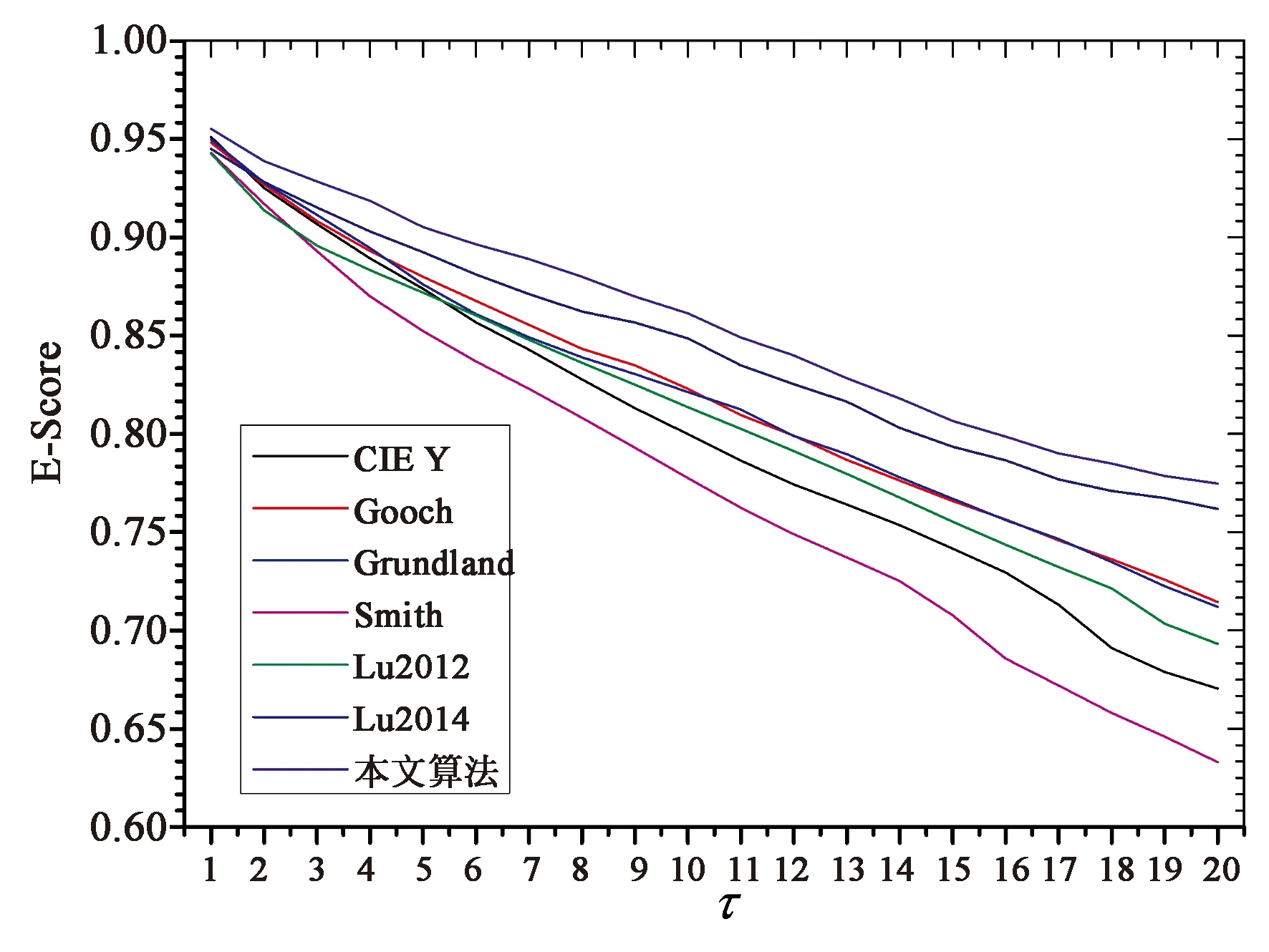
图7 E-Score随阈值τ变化的曲线图

从图7中可以看出，本文算法的E-Score评价结果明显优于其他6种灰度化算法，进一步说明了本文算法能够有效保持输入彩色图像的对比度和彩色内容信息。

在相同的测试条件下，利用本文算法与其他6种算法对4幅不同尺寸的图像进行灰度化实验，各算法的运行时间如表3所示。

表3 不同灰度化算法的运行时间

Tab.3 Running time of the different decolorization algorithms s

算法256×192320×240512×3841 024×768CIEY0.025 0.0440.103 0.381 Gooch496.569 1 184.733 7 914.752 >>5 hGrundland0.568 0.909 1.945 5.410Smith2.453 3.557 7.967 24.320 Lu20120.238 0.358 0.566 3.459 Lu20140.193 0.236 0.459 2.528 本文算法0.571 0.859 1.813 6.149

由表3可以看出，本文算法在计算效率方面并不占优势，仅优于Smith和Gooch算法，这是由于本文算法中需要对图像进行多尺度多方向分解和重构，消耗了计算时间，但随着计算机硬件配置的提升和算法的不断优化，本文算法的计算效率也会得到相应的提高，能够较好地平衡灰度化效果和计算效率间的矛盾。

4 结 论