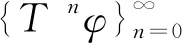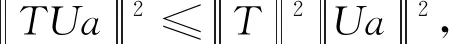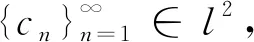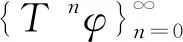K-框架的算子迭代表示

林焕程,朱玉灿

(福州大学数学与计算机科学学院,福建 福州 350108)

0 引言

在科学技术飞速发展的推动下,包括框架理论在内的许多理论知识在计算机算法中的可行性越来越被重视,并且涉及迭代形式的结论在算法中相比其他形式更容易实现.在Gabor框架与小波分析的研究中,Gabor系统或小波系统可以用l2()上一些给定的算子来定义,如以下三种:a∈,Ta(f(x))=f(x-a);b∈,Eb(f(x))=exp(2πibx)f(x);利用上述的算子,l2()上的Gabor系统表示为:

{EmbTnag}m,n∈={exp(2πimbx)g(x-na)}m,n∈

其中:a,b>0为常数,g∈l2()是给定的函数.此外,由函数f∈l2()生成的二进小波系统也可以用类似的算子迭代形式来表示:

更多有关Gabor系统或小波系统的结论参见文献[1-2].本研究旨在探讨Hilbert空间H中一个算子迭代表示的序列与K-框架以及K-Riesz基之间的联系,并且与一般框架中的对应结论进行对比,推广已知的研究结果.

以下先回顾一些有关框架、K-框架、K-Riesz基等本研究将涉及的定义,其中以H表示一个可分的复Hilbert空间,为正整数集.

1 预备知识

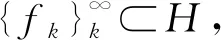
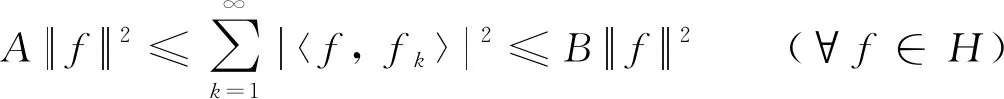
(1)

由定义1可知H的框架也是一个Bessel序列,由文献[1]中的引理3.2.1,可定义如下的有界线性算子:

U:l2()

(2)

定义2设K:H→H为非零的有界线性算子,如果存在A,B>0满足:

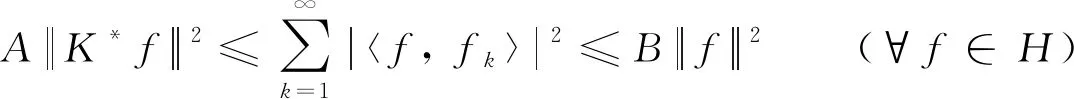
(3)

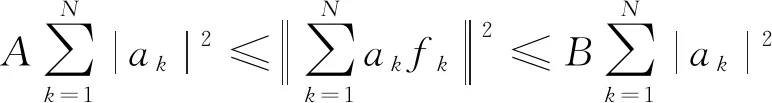
(4)

由于受到近年动态采样研究成果[5]的启发,文献[6-10]对于以如下算子T的迭代形式表示的框架:

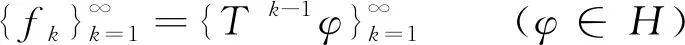
(5)

进行了一系列的研究,得到了关于T的性质以及有关框架的稳定性的结论.以下是更加一般的形式,

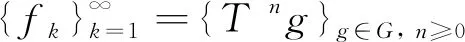
(6)

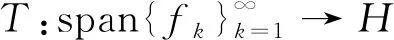
在以下内容中,H表示一个无穷维复可分Hilbert空间,记B(H)为H上的有界线性算子全体,算子K∈B(H)且K≠θ(零算子),R(K)与N(K)分别表示有界线性算子K的值域与核,I为H的恒等算子,为复数集.

2 主要定理与结果

下面将探讨何时一个K-框架能够具有算子迭代表示.以下的引理1～2是一般框架和K-框架的等价刻画,体现了K-框架与框架最重要的不同; 引理3的提出是为了对本研究中讨论的一种特殊的迭代算子进行定义.

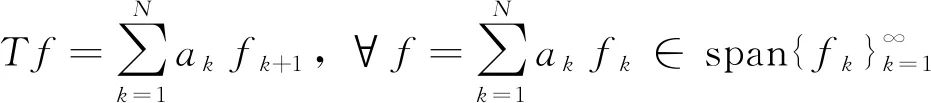
(7)

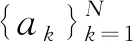
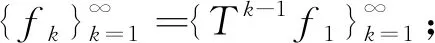
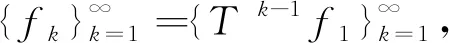
(8)

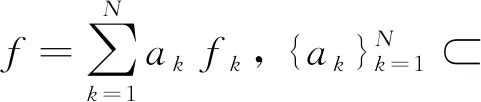
(9)

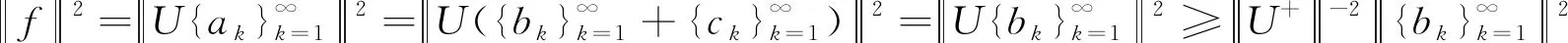
(10)

由式(9)可知：

(11)

即T是有界算子.

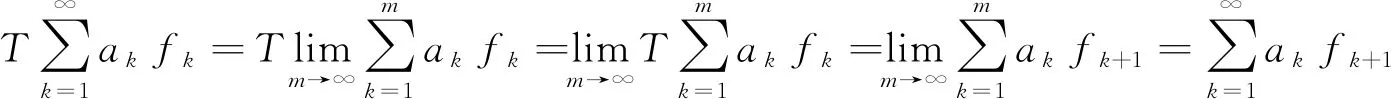
(12)

其中m∈，故对于任意根据式(12) 可得：

即N(U)右平移不变,证毕.

注1文献[8]中证明了对于一般框架而言,由式(7) 定义的迭代算子有界当且仅当合成算子的核满足右平移不变,而定理1中1) 多了一个合成算子闭值域的条件,这表明即使在算子迭代表示序列中,K-框架与一般框架也有很大的不同.以下给出一个例子说明,当一个算子迭代表示的K-框架的合成算子U不具有闭值域时,仅有N(U)右平移不变的条件将得不到迭代算子有界的结论.

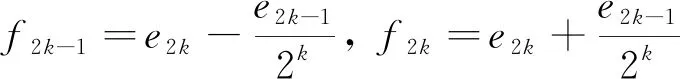
(13)

所以当k→∞时,上式趋于∞,即迭代算子T无界.

接下来考虑一个序列已经具有有界算子迭代表示时,该序列与K-框架的关系,下面给出一个必要条件.

又因为φ∈R(T),所以Kf∈R(T),由Kf在R(K)中的任意性知R(K)⊂R(T),证毕.

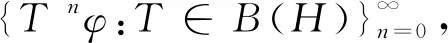
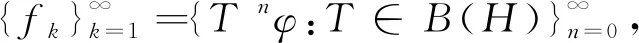
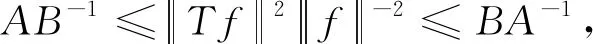
注4文献[8]指出,对于H中任意的Riesz基,均有有界线性算子迭代表示,上述定理3说明了在定义4给出的K-Riesz基的定义下,任意K-Riesz基也均有有界线性算子迭代表示,并给出了具体的迭代算子的界,推广了文献[8]中的结论.

根据上述定理3,可以看出每一个K-Riesz基都可以用算子迭代表示的形式来表示,以下讨论H中一个具有算子迭代形式的K-框架成为一个K-Riesz基所需要的条件,以及一个K-Riesz基在具有算子迭代形式时所能得到的结论.

引理5[4]设H1与H2为两个可分的复Hilbert空间,K:H1→H2为闭值域有界线性算子,则存在K的唯一有界线性伪逆算子K+使得:

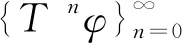
①U*T*是满算子;