基于稀疏表示的时间序列最近邻分类
2020-04-07杨冠仪於志勇郭文忠黄昉菀
杨冠仪,於志勇,郭文忠,黄昉菀
(福州大学数学与计算机科学学院,福建省网络计算与智能信息处理重点实验室,福建 福州 350108)
0 引言
时间序列数据随处可见,并且每时每刻都在生成,如居民用电记录、温度变化、心电图、网络流量数据等.相关研究中,时间序列分类(time series classification,TSC)问题是其中的热点问题之一.分类最终结果受到数据质量、数据相似性和分类器的优劣共同影响.研究表明,基于动态时间弯曲(dynamic time warping,DTW)距离的最近邻分类器具有相当优秀的分类效果[1].DTW能够有效解决时间序列的不等长和局部形变问题[2].然而该距离基于动态规划思想,具有较高的时间复杂度且对噪声敏感.为提高DTW的度量效果,产生了许多围绕DTW的研究工作.FastDTW[3]通过将序列投射到不同分辨率空间并产生多层最佳弯曲路径的方法来加速DTW距离的计算.LB_Keogh和LB_Improved[4]分别通过限制搜索区域以加速计算.DDTW[5]计算每条待比较序列的斜率,用以替代原序列的点值,以解决DTW的“奇异”问题.WDTW[6]通过添加权重对具有相位差的时间序列点进行惩罚以避免由异常点带来的干扰.此外,有研究者借鉴字符串处理的思想,提出了如LCSS、ERP[7]、TWED[8]等基于编辑距离的方法,同样有效地提高了时序数据分类的精度.
考虑到现实生活中的时序数据存在一定的噪声干扰,本研究认为在进行距离度量之前,有必要对数据进行降噪处理.目前常用的降噪方法有离散余弦变换(discrete cosine transform,DCT)、符号聚合近似(SAX)、奇异值分解(SVD)等[9].稀疏表示在信号领域和图像领域有着广泛的应用,如人脸识别、图像重构[10]、图像去噪[11].鉴于稀疏表示在图像去噪问题上的良好表现,本研究提出一种基于稀疏表示的最近邻分类模型(SR-1NN),将基于过完备字典稀疏化并重构的序列1NN-EUD、1NN-DTW进行分类.在18个公开的时间序列数据集(UCR)[12]上的实验表明,稀疏表示对于噪声有一定的容忍性,在一定程度上可以提升分类模型的性能.
1 稀疏表示理论
给定长为n的时间序列y=(y1,y2,…,yn)T∈n×1以及一个构建好的字典D∈n×m,稀疏表示认为y可以被近似表示为下式的线性组合:
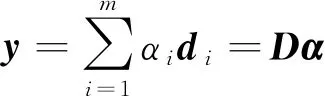
(1)
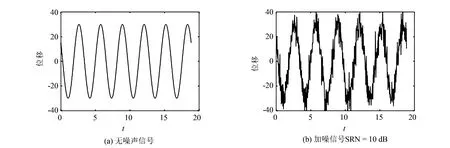
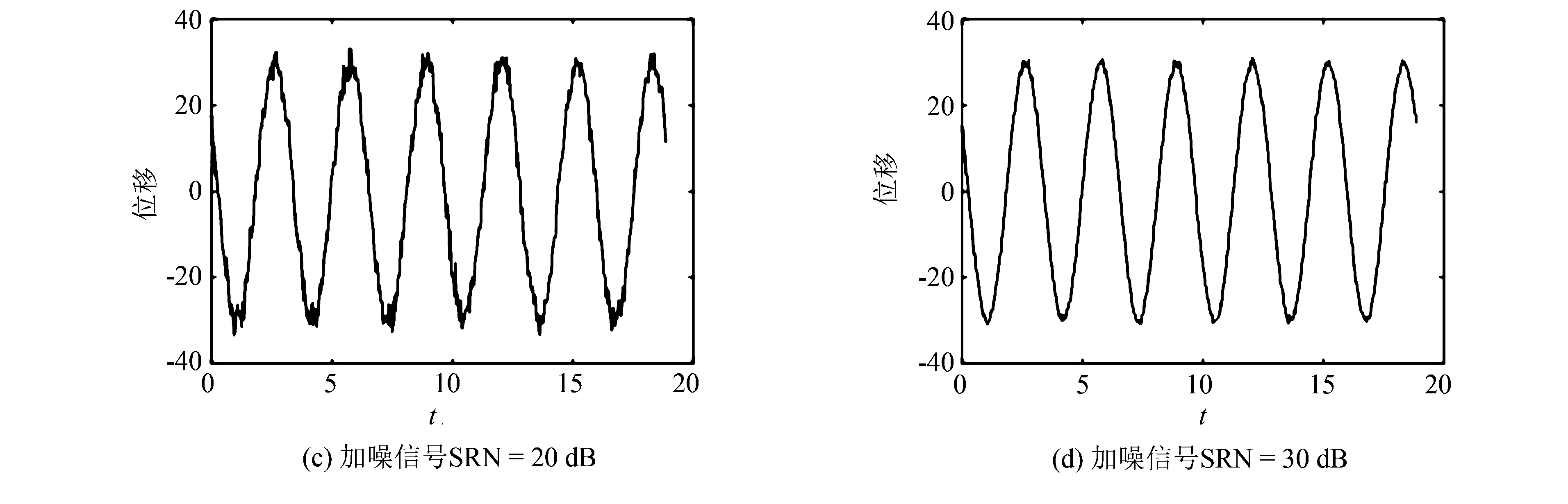
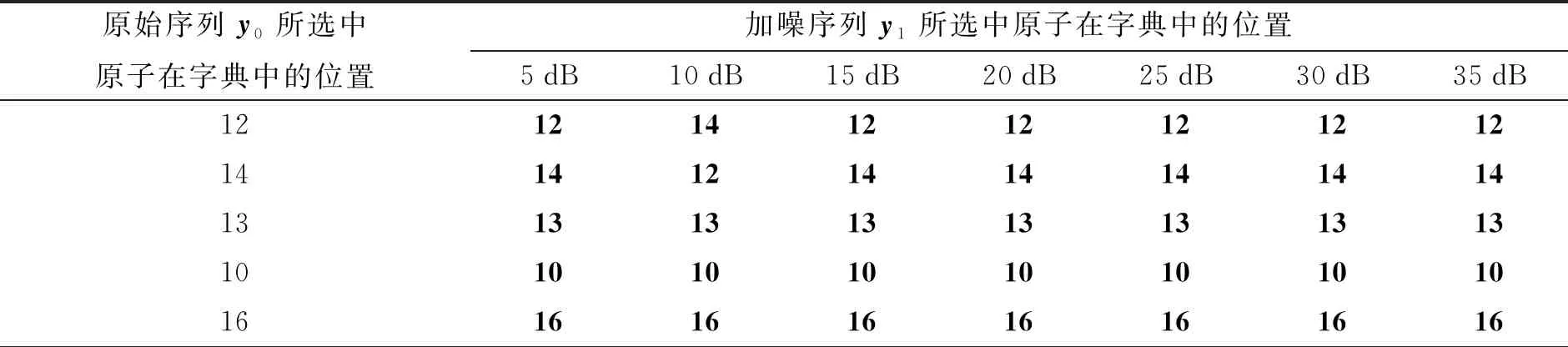
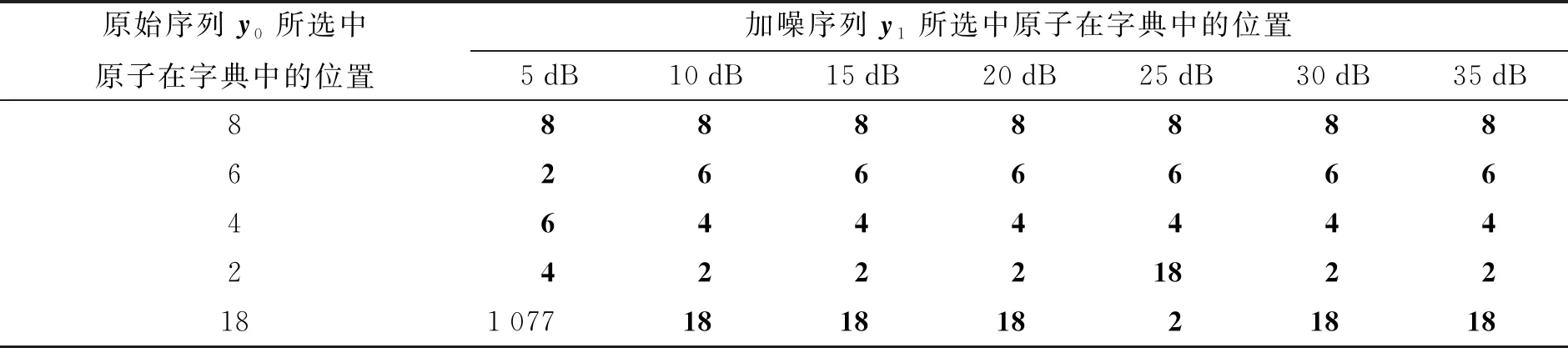
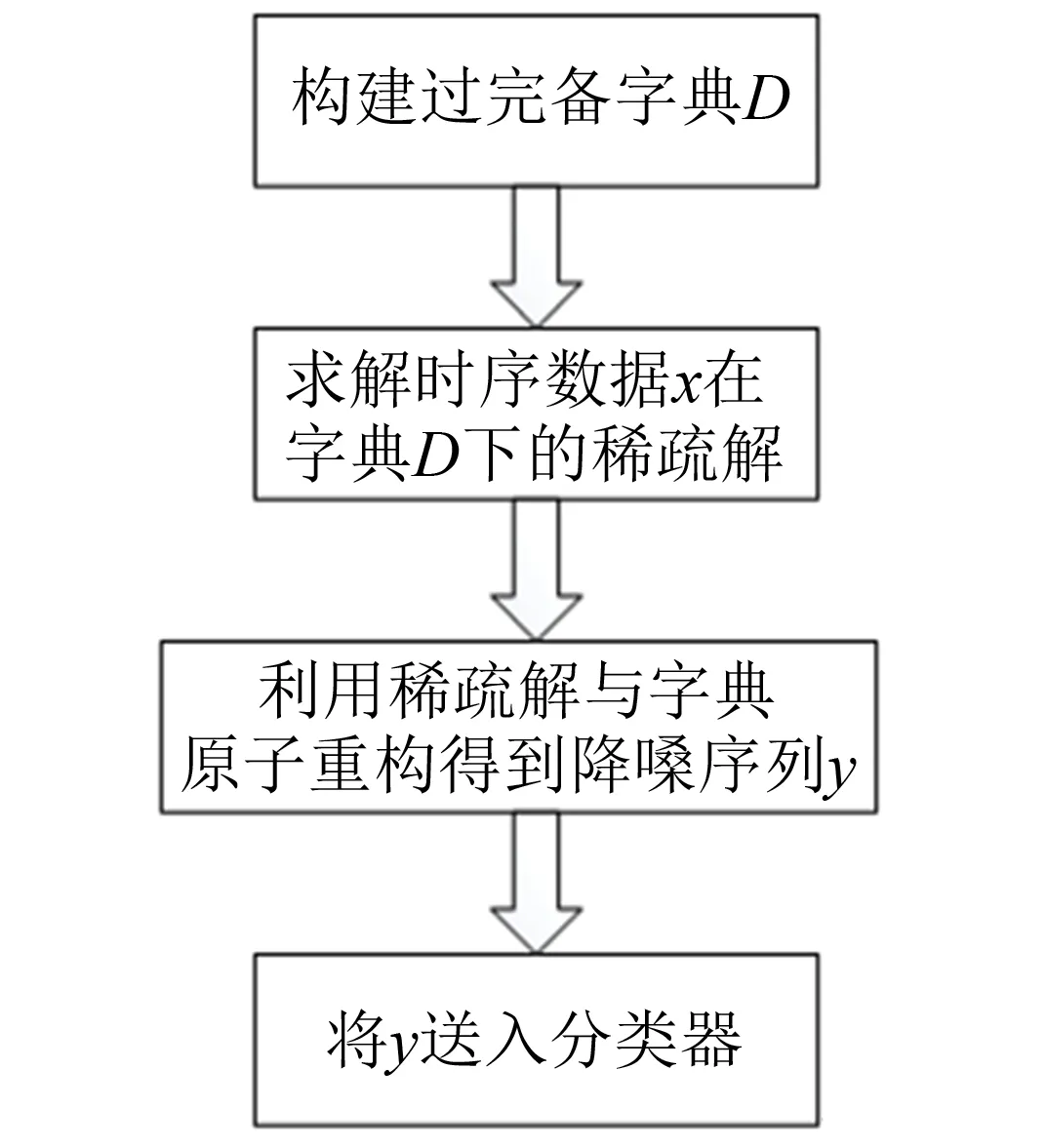
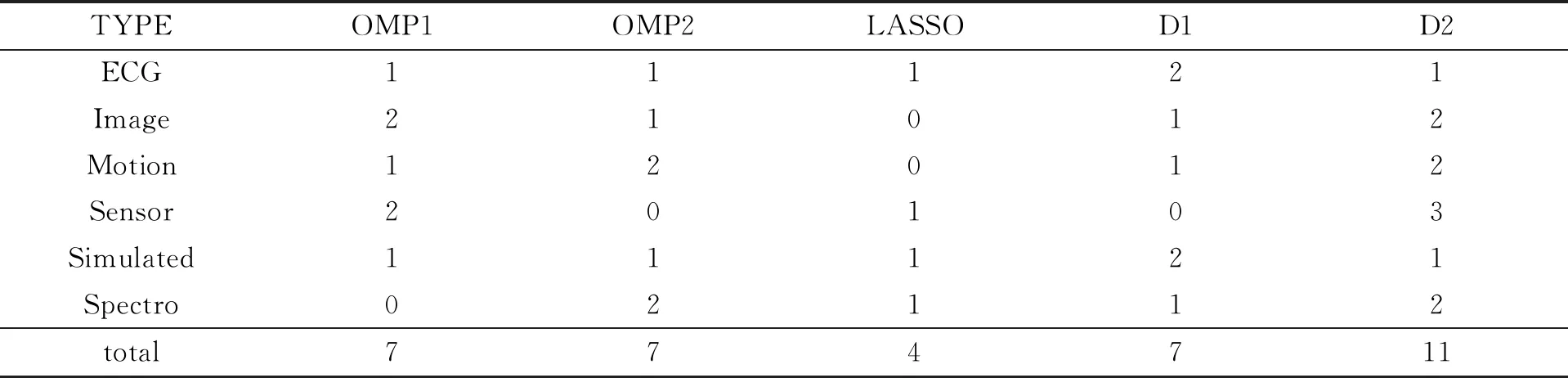
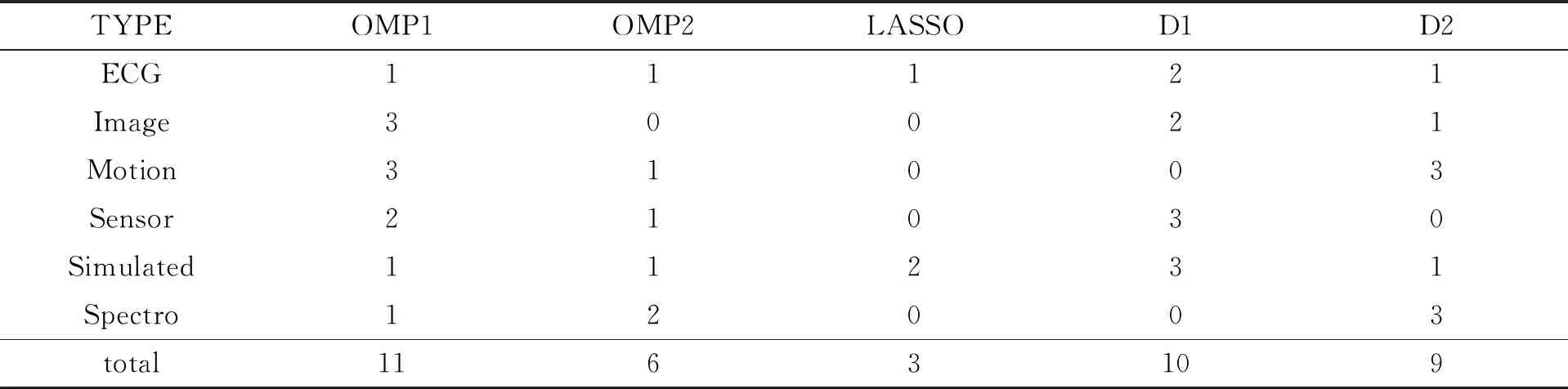
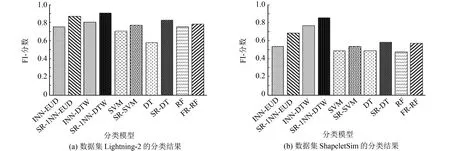
其中:D=(d1,d2,…,dk,…,dm)被称为字典,dk∈n×1称为字典D的第k个原子,α=(α1,α2,…,αm)T∈m×1为y基于字典D形成的转换域的近似表示.如果D是过完备的,即n (2) (3) 其中:ε表示重构误差.上式的对偶形式如下: (4) 其中:k称为稀疏度,表示向量α中非零项的最大个数. 此外,由于重构误差或稀疏度事先难以确定,也可以根据拉格朗日定理同时进行优化.式(3)~(4)可等价地转化为无约束的优化问题: (5) 其中:λ用于平衡重构误差和解的稀疏性,一般来说,λ越大解越稀疏. 由于求解l0范数最小化的稀疏表示问题是一个NP难问题,因此常采用贪心策略或凸松弛策略来得到其近似解.贪心策略在每次迭代时选择最接近原始解的结果,最终通过迭代运算找到符合条件的近似解.此类策略的经典算法为正交匹配追踪(orthogonal matching pursuit,OMP)算法而凸松弛策略则采用将l0范数转换为l1范数的形式,将非凸优化问题转换为凸优化问题进行求解[13].此类策略的经典算法有基追踪(basic pursuit,BP)、最小角归回(least angle regression,LAR)、最小绝对值收敛以及选择算子 (least absolute shrinkage and selection operator,LASSO)等.其中,LASSO是对LAR算法的改进算法,其对应的目标函数如下: (6) 压缩感知理论认为,如果信号是稀疏的、可压缩的,那么利用少部分的观测值即可重构该信号,这些观测值的数量远少于利用如香农采样定律等理论所计算出的数量.受此启发,当时间序列y基于字典可以获得用于重构序列的稀疏表示时,那么稀疏解中所保留的应为原序列y的主要特征,噪声及冗余信息因为稀疏性的限制会被丢弃,这样一来经过稀疏表示后的重构序列参与分类时将比原序列更加容易被区分. 为了证明这一想法,本研究设计了一组实验,根据式(4)求解无噪序列与加噪序列基于过完备字典的稀疏解,并观察求解过程中算法选中的原子及其对应的系数值.实验中采用OMP算法,通过将稀疏度设为20来求解无噪序列与加噪序列的稀疏系数.无噪序列y0是由方程y=30 sin(2t+150°)生成的包含541个采样点的时间序列,过完备字典D的原子数设置为2倍的采样数,即1 082个.加噪序列y1是通过在y0中添加高斯白噪声生成的,其信噪比分别为5、10、15、20、25、30、35 dB,信噪比值越小,代表序列所含噪声越大.图1展示了原始无噪序列以及信噪比分别为10、20、30 dB的加噪序列. 图1 原始序列与加噪序列的可视化图Fig.1 Visualization of the original sequence and the noisy sequence 表1展示了当稀疏度为20时,无噪序列y0和加噪序列y1在同一个字典中选中原子的位置信息,其顺序按稀疏系数从大到小排列.从表1中不难发现,具有不同信噪比的加噪序列所选中的前9个原子与无噪序列选中的除顺序外完全相同.随着信噪比的增大,加噪序列与无噪序列选中的相同原子的个数逐渐增加.当信噪比达到35 dB时,二者所提取的原子完全相同.这充分说明,序列稀疏化后,先保留的是主要特征.而当通过稀疏表示保留序列的主要信息后,可通过剔除冗余信息,有效屏蔽噪声的干扰. 表1 原始序列与加噪序列所选中的原子在字典中的位置 续表1 图2 基于稀疏表示的1NN分类模型流程框图Fig.2 Diagram of 1NN classification model based on sparse representation 基于2.1的结论,本研究提出一个基于稀疏表示的最近邻分类模型(SR-1NN),其流程框图如图2所示. 首先构建过完备字典.字典的构造方法分为解析法和学习法[14].解析法利用预先定义好的数学模型生成字典,如离散余弦变换、离散小波变换等;而学习法则通过训练,从数据中得到字典.为简便计算,采用解析法生成两个过完备字典D1和D2进行性能比较.其中,D1为直接利用DCT变换生成的过完备字典,旨在将时间序列从原始空间转换为特征空间,以获取具有判别力的特征.考虑到时间序列y中可能含有噪声e,字典D2采用由DCT方阵D和单位阵I构成,此时式(1)可转换为以下的形式[13]: y=y0+e=Dα+e (7) 将式(7)采用矩阵的符号表示,可得: (8) 从而可以把式(2)转换为: (9) 在过完备字典构造完后,根据式(3)~(4)或式(6)求解时间序列数据集X={x1,x2,…,xr}基于D1和D2的稀疏解,并结合其选中的原子重构得到降噪后的数据集Y={y1,y2,…,yr}.需要特别说明的是,当利用字典D2重构原始序列时,只需重构D与α而丢弃I与e,就能够实现降噪的效果.最后计算Y中训练数据与测试数据之间的欧氏距离与DTW距离,并结合1NN分类器进行分类. 欧氏距离( euclidian distance,EUD)直接计算序列点对点距离的平方和,DTW采用动态规划思想计算最小距离,这两种度量距离具有无参的特点,因此本研究采用这两种方法进行距离计算,并衍生出SR-1NN-EUD与SR-1NN-DTW模型.将其用于公开的UCR时间序列数据集中,并与1NN-EUD,1NN-DTW的分类结果进行比较,部分数据集信息详见表2. 表2 部分UCR时间序列数据集信息 续表2 UCR时间序列分类数据仓库 (UCR time series classification archive)是由Dau等人共同维护的时间序列公开数据仓库,到2018年为止,该数据仓库已收集128个单变量时间序列数据集以及30个多元时间序列数据集,囊括了Image、Spectro、Sensor、Simulated、Device、Motion、ECG等15种类型的数据.所有数据都已经过z-标准化处理,服从标准正态分布[15].实验选取其中六种类型数据集,以便比较模型在不同类型数据上的差异.数据集的信息如表2所示,表中包含了数据集的名称、类型、类别个数、训练集样本个数、测试集样本个数以及每条时序样本的长度.图3展示了六种类型不同类别的数据曲线. 图3 六种类型数据曲线图Fig.3 Graph of six types of time series 实验比较了时序数据基于字典D1,D2利用OMP算法和LASSO算法求解的分类结果.其中,OMP1是指通过设置稀疏度求解数据的稀疏表示(如式(4)),OMP2是指通过设置重构误差求解数据的稀疏表示(如式(3)),而LASSO算法则针对式(6)进行求解.需要说明的是,式(3)的目标函数涉及稀疏度k的调节,其范围在[1,100]之间.式(4)涉及重构误差ε的调节,而式(6)涉及平衡参数λ的调节.对于这两个参数首先在[0.01,0.9]之间以0.01的步长循环,找到最优参数ε0或λ0,然后在[ε0-0.1,ε0+0.1]的范围内以0.001的步长找最优参数. 本研究采用F1分数用于比较模型的分类性能.F1分数(F1-score)是基于精确率(precision)和召回率(recall)的调和平均,如下面式子所示: (10) (11) (12) 其中:c为类别个数,F1分数的值越高,说明分类效果越好. 3.3.11NN-EUD与SR-1NN-EUD的分类结果比较 通过对三种稀疏求解方法和两种字典组合而成的六种模型的分类结果汇总,表3展示了六种类型数据在SR-1NN-EUD上最好分类结果的数据集个数. 表3 六种类型数据在SR-1NN-EUD上最好分类结果的数据集个数 首先,从字典的角度看,基于字典D2的分类模型其分类效果总体上比基于D1的分类模型效果好.这主要是因为欧式距离对噪声没有任何的处理能力,而基于DCT方阵D和单位阵I的字典D2的分类模型要求在重构原始序列时,只需重构D与α的部分,通过丢弃I与e的信息实现降噪的效果.其次,从稀疏求解方法上看,可以得到以下结论. 1) 采用OMP两种求解方法的分类模型,其分类效果不相上下.根据图3可以发现,对于Image和Sensor类型的数据集而言,其数据特征较为明显,这意味着只需要提取少部分关键原子就足以区分类别.因此上述两个类型的数据集比较适合采用基于稀疏度约束的OMP1模型.实验结果还表明,这些数据集的最好结果对应的稀疏度大部分都在30以下.对于Motion和Spectro类型的数据集而言,其类别间的差异要小于其它类型的数据集.这说明类别间的差异仅仅依靠少数原子进行区分是不够的.因此,更适合采用基于重构误差约束的OMP2模型,因为不同类别的数据基于同样的重构误差有不同的稀疏度,从而能够提取出具有区分能力的特征. 2) LASSO模型的表现整体不如OMP1和OMP2,这主要是因为LASSO模型是在重构误差和稀疏度之间通过调整参数λ取得平衡.这也就意味着其更侧重于所有数据集的平均表现,而很难在一些特别适合于稀疏度约束(如Image类型)或重构误差约束(如Motion类型)的数据集中获得最好的结果. 3.3.21NN-DTW与SR-1NN-DTW的分类结果比较 表4展示了六种类型数据在SR-1NN-DTW上最好分类结果的数据集个数. 首先,从字典的角度看,基于字典D1的SR-1NN-DTW相较于1NN-DTW,在6种类型的数据上的分类效果均有提升.但是从表4中会发现,基于字典D2的SR-1NN-DTW在有些数据集上(如TwoLeadECG、Lightning-7、CBF,等)反而分类效果不如1NN-DTW.这主要是因为DTW距离对部分局部形变具有一定的处理能力,当采用具有降噪效果的字典D2时,双重作用下可能会造成一些有用信息的丢失,从而导致分类精度的下降.因此,对于弹性度量距离而言,基于字典D1的稀疏表示更为合适.其次,从稀疏求解方法上看,采用基于稀疏度约束的OMP1模型的分类效果要好于其他两种算法.这说明DTW距离能够在一定程度上降低过大的重构误差对于相似度度量的影响,从而使得OMP1模型在利用稀疏度提取关键原子的同时,可以避免由于无法兼顾重构误差而造成的分类性能下降. 表4 六种类型数据在SR-1NN-DTW上最好分类结果的数据集个数 3.3.3稀疏表示与其它分类器结合的性能比较 为比较稀疏表示对于最近邻分类器与其它分类器模型的提升效果,本节实验选取了最近邻分类器、支持向量机(support vector machine,SVM)、决策树(decision tree,DT)、随机森林(random forest,RF)四个经典机器学习分类器模型进行比较.其中1NN分类器的距离度量采用欧氏距离和DTW距离.综合考虑3.3.1~3.3.2的实验结果,对于SR-1NN-EUD模型和SR-1NN-DTW模型的稀疏表示求解方法本研究采用OMP1,SR-1NN-EUD模型的字典采用D2,SR-1NN-DTW模型的字典采用D1.SVM使用线性核函数,RF模型的树的数量设置为20.图4展示了数据集Lightning-2和 ShapeleteSim的数据分别采用直接输入和经过稀疏表示重构后输入分类器的分类结果. 图4 数据集Lightning-2和 ShapeleteSim的分类结果Fig.4 The classification result of datasets Lightning-2 and ShapeleteSim 从图中可以看出,稀疏表示对于1NN、SVM、DT、RF模型的分类效果均有提升,但提升幅度有所不同.首先,稀疏表示除了对1NN-EUD明显有效之外,还对于DT具有很好的提升效果,原因在于决策树模型根据数据特征,通过计算信息熵进行树的构建并分类,而经过稀疏表示后的重构序列提取了关键特征,使得决策树模型选择特征更加准确,因而SR-DT的分类精度提升很大.其次,对于RF分类器而言,由于其为基于DT的集成分类器,所以经过改进后的SR-RF的提升空间小于SR-DT.最后,稀疏表示对SVM的提升效果一般,原因在于SVM通过找寻超平面与支持向量来划分数据,在这一过程中,SVM对于数据有一定的抗噪能力和关键特征提取能力,因而稀疏表示虽然对于SVM的分类结果有提升,但提升不大.综上所述,数据经过稀疏表示重构后输入分类器的做法对于不同分类器的性能改善有所不同.针对抗噪能力弱或关键特征敏感的分类器(如1NN-EUD、DT)而言,结合稀疏表示技术均能取得较大幅度的分类精度提升.而对于本身具有一定的降噪和特征提取能力的分类器(如1NN-DTW、SVM)而言,结合稀疏表示技术虽然能提升一定的分类精度,但是提升空间有限. 针对时序数据本身可能存在噪声及冗余信息的问题,本研究借鉴稀疏表示理论在信号处理领域和图像处理领域的出色表现,提出一种基于稀疏表示的时间序列最近邻分类模型,将时序数据基于过完备字典进行稀疏分解并重构,使得重构序列中尽可能少地包含噪声与冗余信息,最后将重构序列进行距离计算并送入最近邻分类器中进行分类.在自拟信号的仿真实验与18个公开数据集上的实验表明,SR-1NN模型能够通过降低原始序列中的噪声及冗余信息,进而提升传统1NN分类器的性能.考虑到过完备字典的设计对稀疏表示的影响巨大,在未来的工作中,将进一步对其进行改进,并通过设置验证集进一步优化模型参数.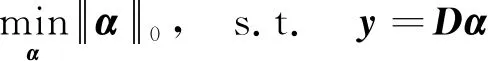

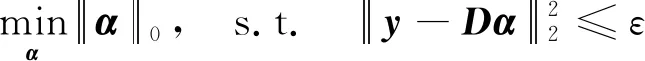
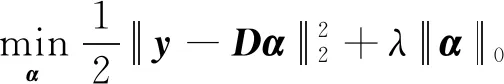
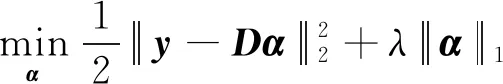
2 基于稀释表示的分类模型
2.1 稀疏表示对噪声的容忍性
2.2 基于稀疏表示的时间序列最近邻分类模型(SR-1NN)
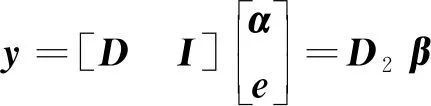
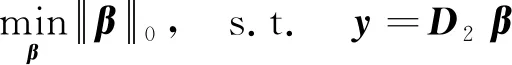
3 实验

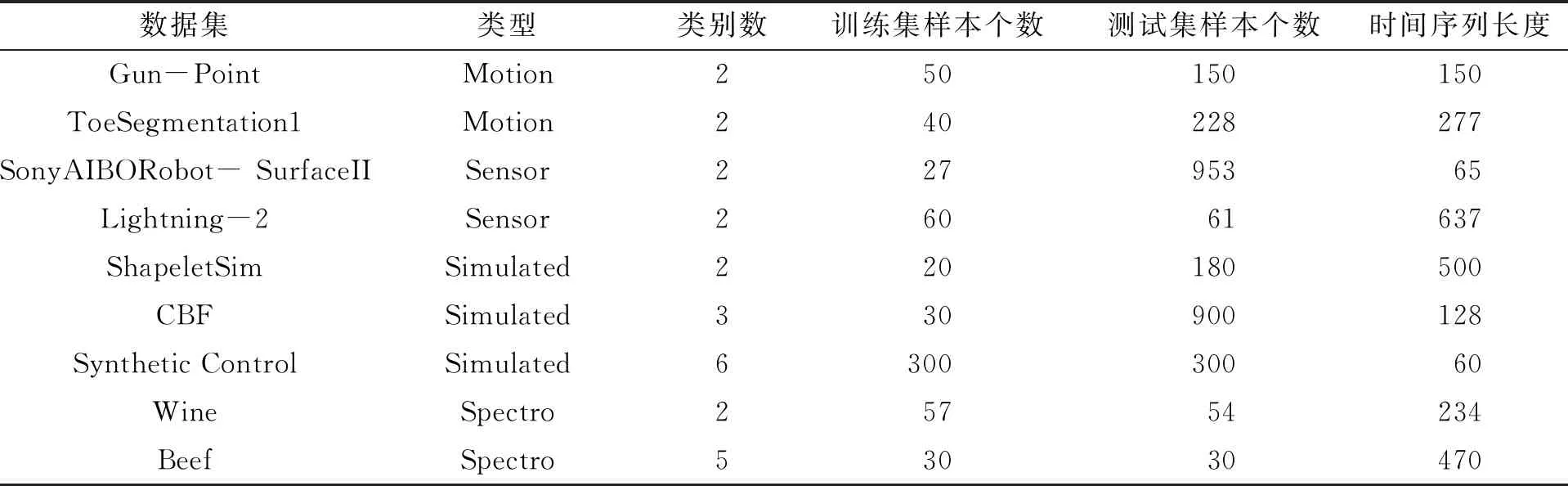
3.1 数据集简介
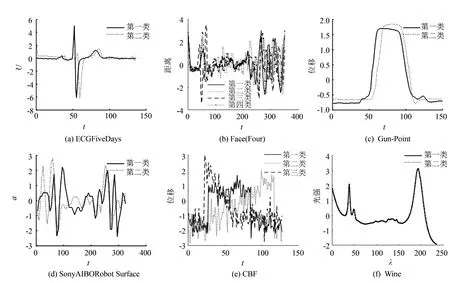
3.2 实验设置
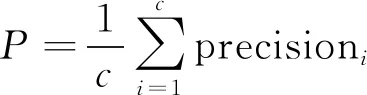
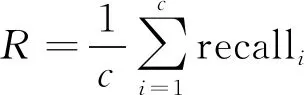
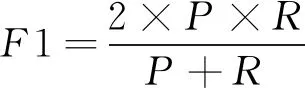
3.3 实验结果及分析
4 结语
