基于高斯混合模型的逆变器故障诊断方法研究

(天津工业大学 电气工程与自动化学院，天津 300382)

0 引言

逆变器是把直流电转变成交流电设备，广泛应用于工业生产的诸多领域，如新能源汽车，UPS电源等。目前国内使用的逆变器主要为以功率半导体为主开关元件的谐振型逆变电路[1]。在电路的工作过程中，会出现元器件性能退化或损坏，导致系统设备连续运行的性能不佳或发生重大故障。如果不能及时发现并定位故障，有可能会造成经济损失甚至危及人身安全。因此逆变器的故障诊断具有十分重要的意义。

故障诊断按照工作任务可以分为故障存在检测和故障类型识别。在实际的工作过程中，为了提高逆变器的可靠性和稳定性，不仅要判断出是否存在故障，还要及时定位故障出现的位置，识别故障类型。目前，国内外对于逆变器故障诊断的研究方法大致可以分为三类[2]：基于数学模型的故障诊断；该方法通过建立逆变器的数学模型来对电路的输出状态进行评估，从而诊断出故障，但是逆变电路结构复杂，建立准确数学模型的难度比较大[3]。例如刘牮等人提出的基于相电压积分的逆变器故障诊断，建立了门极信号和相电压的积分模型[4]，根据相电压的积分作为故障诊断的判据，来区分正常状态和故障状态。基于信号处理的故障诊断。此类方法利对逆变器的输出信号进行变换处理，提取电压或电流信号的时频特征进行故障诊断。例如杨忠林提出的基于小波包分解的逆变器开路故障诊断方法，将直流侧电流信号进行小波包分解，提取分解系数的均方根值，作为开路故障诊断的判据。基于机器学习的故障诊断方法。该方法利用故障的特征数据，通过监督学习的方法，训练出故障诊断模型，进行故障检测和分类。如文献[5]提出的基于隐藏层神经网路的逆变器故障诊断方法。该方法是一种简化的神经网络方法， 训练起来比较容易，但是对于训练数据要求较高。

本文提出了一种基于数据处理和机器学习相结合的逆变器故障诊断方法。首先进行数据采集，采集逆变电路中的两个开关器件和谐振电阻开路故障时逆变器输出的电压信号，然后使用信号处理的方法提取电压信号的时域特征和频域特征。利用时频特征训练高斯混合模型，确定高斯混合模型的参数。训练好的模型可以用来进行故障诊断。最后，使用simulink搭建了逆变电路的模型，进行仿真实验。仿真结果表明该模型的运行速度快且具有较高的诊断精度。本文提出的故障诊断模型，易于实现，可以应用于工业现场的逆变器故障诊断，也可以应用于其他领域的故障诊断。

1 逆变电源的故障分析

逆变电路的故障主要可以分为两类，突变型故障和渐变型故障。突变型故障是指逆变器的一些元器件短路或开路会导致系统瞬间无法运行；而渐变型故障发生时，系统的性能退化，如果长时间运行于这种状态下，会使系统部件或负载产生损坏。渐变型故障更加难以发现，因此，本文主要针对渐变型故障进行分析和诊断。

并联谐振型逆变电源的逆变回路电路原理图如图1所示。逆变回路部分包括一个直流源DC，四个开关管VT1-VT4，谐振电阻R，谐振电感L，谐振电容C等元器件。并联谐振型的逆变电路的故障类型有单开关管开路，双开关管开路，三开关管开路，四开关管开路以及谐振器件开路等。一般，双管、三管、四管开路的概率比较小[6]。因此，本文选择单开关管开路故障，以及谐振器件故障作为研究对象进行故障分类识别。本文把正常状态作为一种特殊故障状态来处理，研究4种故障状态：正常状态，VT1开路，VT2开路和谐振电阻R开路。

如果每个故障处设一个故障检测点，检测电压或电流信号，能最直接准确地识别故障的类型和位置。但是这样会使故障诊断系统的复杂度大大增加，尤其是在逆变器结构复杂，故障类型较多的情况下。这种方法并不适合于实际生产。考虑到不同的故障类型会对电路的输出电压产生不同的影响。因此，测得逆变器的输出电压的特征就可以推测出故障的类型。测量输出电压操作简单，易于实现，适合于进行故障诊断。但是故障诊断之前，需要采集大量不同故障类型的数据，才能找到较为准确的故障类型和输出电压的关系。

图1 逆变回路原理图

2 故障特征提取

少中提取有用信息，去除冗余信息，从而使数据维度降低的过程[7]。进行故障诊断需要采集逆变器运行过程中的数据，而电信号采集一般采样频率较高，如果直接用原始数据进行故障诊断，会占用大量存储和计算资源[8- 9]。因此，在故障诊断过程中，特征提取是十分必要的。数据的特征一般分为时域特征和频域特征[10-11]。时域特征描述的是信号随时间变化的关系，时域特征的特点是计算简单，可以直观描述信号。常用的时域特征有平均值，均方根误差，波形因子，裕度系数，波峰系数等；频域特征反映信号的动态特性，常用的提取频域特征的方法有傅里叶变换，小波变换，希尔伯特变换等。本研究分别提取故障数据的波峰系数和小波能量熵作为时域和频域特征，组成二维特征向量，作为故障诊断的依据。

波峰系数是信号峰值与均方根值的比值，是信号平稳度的一种度量。交流电是正弦波，其波峰系数约为3。当系统发生渐变型故障，波形发生变化，其波峰系数也会相应改变。因此，本研究选择波峰系数作为故障的时域特征。小波变换是近年来发展起来的一种多尺度信号分析方法。该方法通过平移和缩放运算把信号分成低频和高频部分，从而有效提取信号的时频信息。熵是指体系的混乱程度，用来表示能量在空间中的分布均匀程度。小波能量熵是小波各个成分的能量在子空间分布无序程度的一种度量。本文使用小波能量熵提取故障数据的频域特征。

原始信号经过小波变换之后，可以获得不同尺度下的子信号。每个尺度下的信号都有一个小波系数。我们定义单一尺度下的小波系数的平方之和为该尺度下的小波能量。

其中:J是小波变换分解的层数，Cj(k)是小波系数。

将小波能量标准化，则有:

其中:Etotal是所有小波能量的和。根据熵的定义，可以获得以下小波熵:

如果小波能量熵较大，说明原始信号在各个子频带上较分散；如果小波能量熵较小，说明原始信号集中分布在某些子频带，它能够作为频域特征来区分不同类型的数据。

3 用于诊断的高斯混合模型

经过数据采集和特征提取，最后需要一个分类器来进行故障分类识别。高斯混合模型(Gaussian mixture model, GMM)是一种非常基础的概率统计模型，由若干个基于高斯概率密度的子模型组合而成。高斯混合模型的优点是它的结果是基于概率值的。我们可以计算经验置信区间，然后根据这些信息，在某个感兴趣的区域重新拟合，进行预测。使用高斯混合模型时，还可以根据需要指定不同的核函数。而且高斯混合模型可以通过增加子模型的数量来拟合较复杂的数据分布，灵活性好，能够更好地描述数据结构。

高斯混合模型的定义如下：

在数理统计领域中，一维高斯分布的概率密度函数如下所示：

其中：μ是高斯分布的均值，σ2是高斯分布的方差。

对于多维变量X=(x1,x2,…,xn)，假设其服从联合高斯分布，则其概率密度函数为：

其中：u是多维变量X的均值，∑是多维变量X的协方差矩阵。

当n=2时，二维变量可以拟合出二维坐标平面中椭圆形数据的分布。但是实际工程中的数据分布往往比较复杂，单一的高斯模型很难准确地拟合出数据的分布概率。这时，通过求解多个高斯模型，赋予每个模型一个权重，就形成了高斯混合模型。不同的权重决定了每个高斯函数在GMM中所起的作用。K个高斯模型组成的高斯混合模型的概率密度如下所示：

其中：N(x|uk,∑k)是第k个高斯模型的概率密度函数。πk是第k个模型被选择的概率。

如果高斯模型的数量足够多，通过调整每个高斯模型的均值方差和每个高斯模型的权重，这个高斯混合模型可以准确拟合任意的样本分布。

高斯混合模型的参数为(μ,∑,π)，最大期望算法(Expectation-Maximization algorithm， EM)通常被用来求解高斯混合模型的参数。EM算法一种通过迭代进行极大似然估计的优化算法。通常用于对包含隐变量或缺失数据的概率模型进行参数估计。EM的标准计算框架由E步(Expectation-step)和M步(Maximization step)组成。算法具有收敛性，可以迭代求得最优值。EM算法的步骤如下所示：

1)设置每个模型的初始值πk，μk和∑k。

2)E step。

根据当前的πk，μk和∑k计算每个数据xi由第k个模型生成的后验概率：

3)M step。

根据E step中计算的γ(i,k)再重新计算πk，μk和∑k：

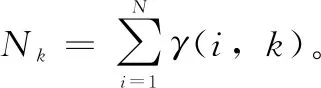
4)计算对数似然函数。

5)重复2)～4)步，直到对数似然函数收敛为止。

上述迭代方法一定会使对数似然函数收敛于局部最大值。也可以证明该局部最大值就是全局最大值。

在求解GMM模型的过程中，用到了全概率公式和朴素贝叶斯公式和极大似然算法。 GMM算法所得到的对数似然概率不仅包含了数据点的标签，也包含了数据点属于这一标签的概率。这一点对于故障的识别与判断具有重要的意义。

4 实验仿真

为了验证本文提出的基于高斯混合模型的并联谐振型逆变器的故障诊断方法，在simulink中搭建了并联谐振逆变器的仿真模型，进行故障诊断。故障诊断的主要步骤如下所示。

4.1 数据采集

不同的故障类型会产生不同的数据，这些数据都能从逆变器输出电压反映出来。因此，仿真实验采集的数据为输出电压。在simulink模型中模拟出正常状态，VT1开路，VT2开路和谐振电阻R开路这四种工作状态并记录输出电压。

4.2 数据预处理

数据预处理是对数据提前进行处理和修正。采集的原始信号可能会出现异常点或缺失点，在数据预处理时需要进行删除或补全，以避免对后续计算产生干扰。数据预处理还包括标准化、归一化、特征转换等。

4.3 特征提取

实验采集的电压信号数据量大，含有较多冗余信息，需要进行特征提取。本实验提取的特征是波峰系数和小波能量熵。它们组成二维特征向量，作为高斯混合模型的输入。

4.4 模型训练

模型训练是使用提取的特征数据来确定高斯混合模型参数(μ,∑,π)的过程。本仿真实验使用二维时频特征训练高斯混合模型，混合模型的数量n=7。

4.5 模型测试

模型测试是使用从原始数据单独留出的样本，对训练好模型的故障识别能力进行评估的过程。模型测试可以得到模型的准确率，评价模型的好坏，作为模型调整的依据。如果故障诊断模型在训练时具有较高的准确率，而在测试时准确率较低，说明训练的模型可能存在过拟合现象，需要对训练的模型进行调整，需要加入正则化项或提前结束训练来减少过拟合现象。

仿真实验的仿真电路如图2所示。该电路是一个典型的并联谐振逆变电路，这种电路基于并联谐振的原理，把换流电容和负载电路并联，广泛应用于中频逆变器上。逆变桥由四个臂组成，每一个臂由一个晶闸管和限流电感串联而成。负载回路由电容C和感应线圈L、谐振电阻R并联组成。模型中的参数为输入电压源为直流250 VDC，谐振电容0.01 F, 谐振电感0.001 H。针对以上分析的四种故障类型，仿真得到四种电压波形如图3所示。仿真实验采集了4种故障类型的数据一共3 000组，其中2 000组数据用来训练，1 000组数据用来测试。

图2 逆变器仿真原理图

对四种故障分别提取时域的波峰系数和频域的小波能量熵，特征分布的部分结果如图4所示。从图中可以看出，VT2故障较容易区分，VT1故障、谐振电阻故障和正常状态的特征比较接近。使用2 000组特征数据训练高斯混合模型，训练的参数为：高斯模型7个，协方差类型是full，迭代停止阈值是1e-3。训练后得到特征数据的负对数分布如图5所示，从图中可以看出，越接近样本点，概率值越大，说明训练的模型准确有效。最后使用1 000组4种类型的数据输入模型进行测试。通过EM算法可以计算输入的测试数据属于每种故障类型的概率，并把概率最大的那个故障类型判断为该条测试数据的故障类型。EM算法预测的结果在表1中列出。该模型对于正常数据，模型的识别率为100 %；对VT1故障的识别率为75.2 %；对VT2故障的识别率为100 %，对谐振电阻R故障的识别率为97.91 %。总的故障识别率达到93.2 %。本文提出的逆变器故障诊断方法能较好地将故障识别。

图3 四种故障类型的输出电压数据

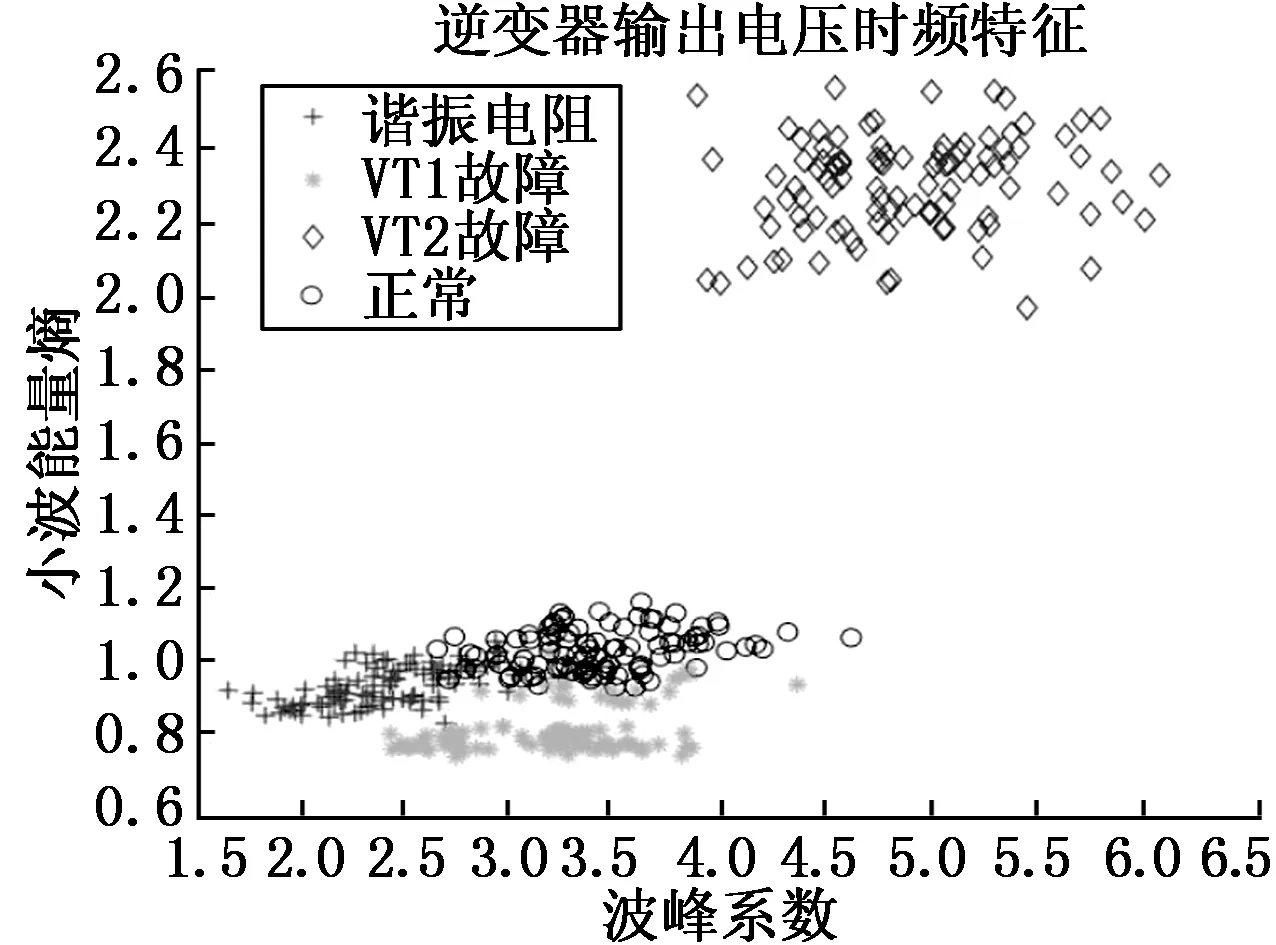
图4 四种故障类型的特征分布

图5 训练后的高斯混合模型特征概率分布

表1 四种故障诊断正确率

5 结论

针对并联谐振型逆变器，本文提出了一种基于高斯混合模型的逆变器故障诊断方法。采集并分析逆变器输出电压数据，提取电压数据的波峰系数和小波能量熵作为故障数据的特征。用特征数据训练高斯混合模型，最后使用EM算法对输入数据进行识别分类，确定故障的类型。为了验证所提出故障诊断方法的可行性和准确率，使用simulink建立了谐振型逆变器的电路模型，进行了仿真实验。仿真结果表明，对于4种类型的电压数据，该诊断方法的准确率可以达到93.2 %，说明本文建立的模型具有可行性和较高的准确率，能够满足实际应用需求。

本文提出的故障诊断方法，操作简单，容易实现，可以为其他类型的逆变器故障诊断提供参考依据，也可以推广于其他应用领域的故障诊断。