基于BDS-3和Galileo多频信号弱电离层组合的中长基线RTK定位方法

高 旺，潘树国，黄功文

（1. 东南大学 仪器科学与工程学院，南京 210096；2. 自然资源部大地测量数据处理中心，西安 710054）

随着我国北斗三号（BDS-3）卫星系统的正式建设完成（2020年7月31日）以及欧洲Galileo 系统、美国GPS 系统等的建设完善，卫星导航已经进入多系统融合发展时代。此外，各个系统均陆续开始支持多频（≥3 频）信号。当前，BDS-3 系统在 B1C(1575.42 MHz) 、 B1I (1561.098 MHz) 、 B2a(1176.45 MHz) 、 B2b (1207.14 MHz) 和 B3I(1268.52 MHz)上播发五个频率信号[1]，Galileo 系统在E1 (1575.42 MHz) 、 E5a (1176.45 MHz) 、 E5b(1207.14 MHz) 、 E5 (1191.795 MHz) 和 E6(1278.75 MHz)上同样播发五个频率信号[2]。利用多系统多频信号优势，除了能够增加观测冗余，还能构建出一些具有长波长、弱电离层影响以及低噪声等优良特性的观测值组合，对于整周模糊度解算、周跳探测以及定位解算性能均具有较好的提升[3]。

对于卫星导航中长基线定位，整周模糊度的解算是实现厘米级定位的前提和必要条件。传统的双频观测模式通常采用“三步法”进行整周模糊度解算定位[4]，即首先利用双频宽巷载波和窄巷伪距，采用宽巷相位和窄巷伪距组合解算宽巷模糊度；其次基于载波和伪距无电离层组合，解算窄巷模糊度浮点解；最后带入固定的宽巷，恢复窄巷模糊度的整数特性，并进行搜索固定。解算过程中，宽巷模糊度解算效果直接影响后续窄巷模糊度解算的可靠性。受限于伪距观测噪声和多路径误差的影响，宽巷相位和窄巷伪距组合求解宽巷模糊度需要多个历元进行均值滤波，且对伪距观测质量具有较高的要求。近年来，随着北斗二代（BDS-2）和GPS 陆续播发三频信号，众多学者也提出了基于三频的中长基线模糊度解算方法，总体思路是利用三频观测值中超宽巷/宽巷模糊度易于固定的优势，依次分步和约束解算超宽巷、宽巷和窄巷模糊度，如文献[5]在各步骤解算中进一步引入伪距观测值，构建了基于最小噪声的无几何、无电离层（GIF）组合；文献[6]提出了一种估计倾斜电离层延迟的三频模糊度分步解算方法，提升了BDS-2 中长基线基础模糊度解算可靠性。总的来说，无论是基于双频还是三频的模糊度解算，大多是优先解算超宽巷或宽巷模糊度，其次固定基础模糊度，这也意味着实时定位时终端用户需要同时接收多个类型观测值，以组成不同的观测值和模糊度组合，对实时数据传输量具有较高的要求，对于基于短报文或信标台等具有较小数据播发能力的差分定位应用具有一定的挑战。

基于BDS-3 的新频率信号，文献[7]研究了一种具有弱电离层影响的窄巷载波组合，该组合在保持整数可解特性的同时，还具有与传统双频无电离层组合相当的有效波长。在该研究的基础上，本文将系统阐述适用于中长基线的弱电离层观测值组合选取准则，分析挖掘BDS-3 和Galileo 五频信号中的最优弱电离层组合观测量，实施BDS-3 和Galileo 的组合定位，并与常规双频无电离层组合的定位性能进行分析对比，实现基于较小数据传输量的中长基线RTK 定位。

1 BDS-3 和Galileo 五频观测值组合模型

不失一般性，考虑长基线对流层和一阶电离层延迟影响的载波和伪距观测方程可表示为[8]：

式中，Δ 表示站间星间二次差分算子；φ和P分别表示以距离为单位的载波和伪距观测值；下标j表示卫星观测频率；ρ表示站星距离；T表示对流层延迟;I1表示对应第一个频点上的一阶电离层延迟；表示第j个频点上的电离层延迟系数，fj表示信号频率；λ表示载波信号波长；N表示整周模糊度；ε表示观测值噪声。基于式(1)所示观测方程，可进行观测值的线性组合。对于五频情况，按周以整系数组合的观测值可表示为[9]：

式(2)相对应的观测方程可表示为：

式(2)(3)中，ik(k= 1,2, … ,5)表示组合系数。组合观测值相应的频率f(i1,i2,i3,i4,i5)、波长λ(i1,i2,i3,i4,i5)、电离层延迟系数η(i1,i2,i3,i4,i5)、整周模糊度 ΔN(i1,i2,i3,i4,i5)以及噪声放大系数μ(i1,i2,i3,i4,i5)可表示为：

对于式(3)，进一步考虑电离层延迟影响和观测噪声对整周模糊度解算的影响，可得模糊度电离层延迟影响系数β(i1,i2,i3,i4,i5)和模糊度噪声放大系数ω(i1,i2,i3,i4,i5)分别为：

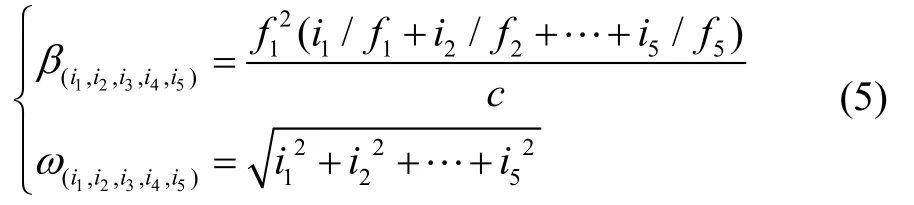
式中，β以 cycle ⋅ m-1为单位，表征单位电离层延迟对模糊度解算的影响；ω表征组合后的载波噪声对模糊度解算的影响。

2 BDS-3/Galileo 弱电离层组合观测量选取

基于式(2)-(4)所示的组合观测值模型，考虑组合系数的任意性，理论上可构建出无穷多个组合观测值。由于本文的关注点为寻找可直接用于长基线定位的弱电离层组合观测量，因此对组合观测量的特性做以下几点限制：

（1）组合后的观测值无论对于模糊度解算还是定位解算都应具有足够小的电离层延迟，以适应长基线复杂电离层情况。以5 m 电离层延迟为例，实现对模糊解算和测距的影响分别小于0.1 周和1 cm，则要求β＜ 0.02，η＜ 0.002；

（2）组合后的观测值无论以周为单位还是以距离为单位均应具有较小的噪声，以保证模糊度的求解可靠性以及厘米级定位精度。其中，以周为单位的噪声较小，决定了组合系数不应过大[10]；以常用的GPS系统双频无电离层组合噪声系数为参照（2.98），要求以距离为单位的噪声放大系数μ应不大于3.0；

（3）组合后的观测值波长不应过小，以保证在模糊度解算过程中能够抵抗残余几何项误差的影响，按GPS双频无电离层组合有效波长为参照（10.70 cm），组合观测值波长不小于10 cm。

基于上述三个条件，以[-10,10]为组合系数搜索区间，遍历BDS-3 和Galileo 满足条件的观测值组合，结果如表 1 所示。表中，BDS-3 的频率顺序为B1C/B1I/B2a/B2b/B3I ， Galileo的频率顺序为E1/E5a/E5b/E5/E6。从表1 中可以看出BDS-3 满足上述条件的观测值组合有4 个，以(2,2,-3,0,0)组合为最优，相比常用的GPS 双频无电离层组合具有相当的波长，且具有更小的噪声，以周为单位和以距离为单位的电离层延迟影响系数均接近于0；Galileo 满足条件的组合有3 个，以(4,-2,0,-1,0)组合为最优，同样具有比GPS 双频无电离层组合更优的性能。

表1 BDS-3 和Galileo 满足条件的弱电离层组合参数Tab.1 Parameters of the ionosphere-reduced combinations for bds-3 and Galileo

3 弱电离层组合（IR）与双频无电离层(IF)组合性能对比

从表1 中可以看出，BDS-3 和Galileo 系统中，各有至少一个可用于长基线定位的弱电离层组合。该弱电离层载波组合直接具备模糊度整数特性，相应的伪距观测值除电离层影响系数正负相反外也具备相同的性能。这表明各卫星仅需使用一个组合后的载波和伪距观测值即可进行长基线定位解算；而在双频情况下，由于在无电离层组合基础上还需要先解算宽巷模糊度，因此需要使用原始的双频载波和伪距观测值，使用非组合模型也同样如此[11]。因此，从实时定位需发送的差分观测值数据量角度来说，使用弱电离层组合观测量可减少一半。此外，使用弱电离层组合无需解算宽巷模糊度，在计算复杂性上相比双频无电离层组合也得到了缩减。

为与常用的GPS 以及BDS-3 和Galileo 系统自身的双频无电离层组合在解算性能上进行对比，表2 给出了GPS、BDS-3 和Galileo 双频无电离层组合相关的特性。其中，BDS-3 采用的是BDS-2 系统中同样具有的B1I 和B3I 频率，Galileo 系统采用的是常用的E1 和E5a 频率。需要说明的是，为便于直接比较，表2 中三种无电离层组合的相关特性均是基于宽巷模糊度已事先解得而计算出的结果。

对比表1 和表2，可以看出表1 中最优的弱电离层组合观测量的波长和表2 中无电离层组合的有效波长基本相当，均在10.5 cm 至11.0 cm 之间；无电离层组合可完全消除一阶电离层延迟影响，最优弱电离层组合也仅残余了较小的电离层影响，即使当双差电离层延迟达到10 m 时，对BDS-3、Galileo 的整周模糊度解算影响也不大于0.05 周，对测距精度的影响不大于5 mm，基本可认为不受电离层误差的影响；观测噪声方面，最优弱电离层组合相比无电离层组合均有一定的优势，BDS-3 和Galileo 的模糊度解算噪声系数分别从6.8751/4.9282 减小至4.1231/4.5826，测距噪声系数从3.5275/2.9783 减小至2.0660/2.4778。

表2 BDS-3、Galileo、GPS 双频无电离层组合参数Tab.2 Parameters of the dual-frequency ionosphere-free combinations for BDS-3, Galileo and GPS

4 解算实验

从上一节的分析可知，使用BDS-3 和Galileo 最优弱电离层组合与双频无电离层组合具有相当的有效波长和电离层抑制性能，在观测噪声方面具有较好的提升。为验证该分析结果，采用一组实测的BDS-3 和Galileo 中长基线数据进行定位解算。该基线数据来源于陕西省某区域参考站网，观测日期为2020年9月22日（24 小时），包含BDS-3 和Galileo 五频观测值，基线长度50.8 km，采样间隔30 s。解算过程中，设定参与解算的卫星截止高度角为10 °；采用卡尔曼滤波进行多历元参数估计，将测站间相对的天顶对流程延迟（Relative Zenith Troposphere Delay，RZTD）作为未知参数解算，求解的参数包括：三个基线分量、RZTD 以及双差整周模糊度。双频无电离层组合中的宽巷模糊度采用多历元平滑解算，取整时设定小数偏差阈值b和精度阈值σ分别为0.2 周和0.1 周，宽巷固定后对应的窄巷模糊度才可进行整数搜索。为减弱非模型化误差对模糊度固定的影响，两种模型中窄巷模糊度对应的高度角大于20 °方可进行整数搜索，整数搜索采用最小二乘降相关（Least-Squares Ambiguity Decorrelation Adjustment，LAMBDA）方法。

该基线观测时段内的BDS-3 和Galileo 可用卫星数如图1 所示，可以看出BDS-3 可用卫星数在7～11颗，Galileo 可用卫星数在4～9 颗，融合后可达12 颗以上。

图1 BDS-3 和Galileo 可用卫星数Fig.1 Visible satellites of BDS-3 and Galileo

相应的定位精度因子（Position Dilution of Precision，PDOP）如图2 所示，可以看出BDS-3 和Galileo 融合后的PDOP 值基本都在2.0 以内，具备较好的定位观测结构。

图2 BDS-3 和Galileo 定位精度因子Fig.2 Position Dilution of Precision (PDOP) of BDS-3 and Galileo

为体现多个时段两种定位模型的定位效果，将24小时数据按每6 小时进行重新初始化，分为四个独立解算时段。图3 给出了两种模型解算过程中的可搜索窄巷模糊度数量。IF 代表无电离层组合，IR 为弱电离层组合。由于无电离层组合模型需要先解算宽巷模糊度，因此在各区段的初始阶段，IF 需要数个历元等待宽巷解算完成，而弱电离层模型（IR）无需解算宽巷可直接进行窄巷模糊度搜索；在解算过程中，伴随着新升起卫星的陆续出现，也存在一些宽巷模糊度尚未固定的情况。总体上，使用弱电离层组合相比双频无电离层组合模型具有更多的可搜索模糊度数量。

图3 可搜索模糊度数量Fig.3 The number of searchable ambiguities

图4 和图5 给出了解算过程中窄巷模糊度解算精度因子（Ambiguity Dilution of Precision，ADOP）和次优/最优模糊度方差比值（Ratio），其分别表征了模糊度求解的先验精度和后验固定效果。当ADOP 值小于0.12 周时，等效于模糊度解算的先验成功率高于99.9%；Ratio 值一般设定为2.0～3.0，大于设定的阈值时认为模糊度可固定，本文采用2.5 作为阈值。从图4可看出，弱电离层组合模型的ADOP 值总体上略小于无电离层组合模型，表明其模糊度解算的精度更高，这与第3 节中的噪声精度分析相一致；在模糊度固定Ratio 值方面，由于参与搜索固定的模糊度个数不同，两种模型的Ratio 值互有高低，总体上水平相当。两种模型四个解算时段的首次固定所需历元数统计如表3 所示，其中首次固定的标志为ADOP≤0.12、Ratio≥2.5。从表3 中可以看出，总体上弱电离层组合模型（IR）首次固定所用历元数少于双频无电离层组合模型（IF）（除时段1 略大于外）。

图4 模糊度精度因子Fig.4 Ambiguity dilution of precision (ADOP)

图5 模糊度固定Ratio 值Fig.5 Ratio of ambiguity fixing

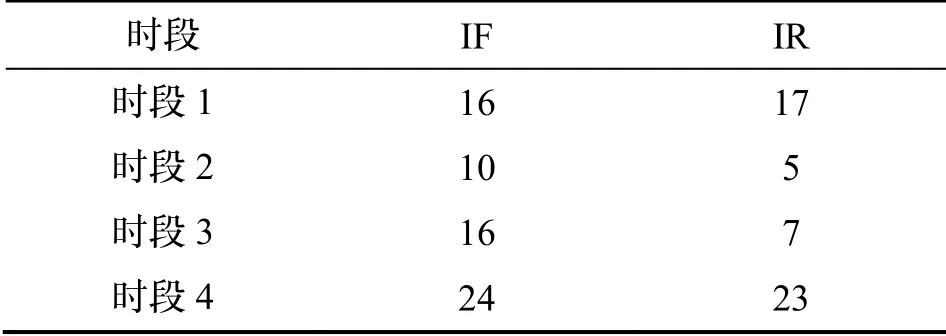
表3 两种模型首次固定时间统计（历元）Tab.3 Time (epochs) to the first fix of the two models

两种模型在北（N）、东（E）和天（U）三个方向上的定位结果如图6 所示，其中包含了浮点解和固定解。在固定解方面双频无电离层组合模型三个方向上的定位精度统计RMS 值分别为0.69 cm、0.64 cm和2.28 cm，弱电离层组合模型RMS 值为0.57 cm、0.57 cm 和1.83 cm，相比无电离层组合模型分别提升了17.4%、10.9%和19.7%，验证了弱电离层组合模型具有更优的定位精度。

图6 多频弱电离层组合模型与双频无电离层组合模型定位精度对比Fig.6 Positioning comparison of the multi-frequency ionosphere-reduced model and dual-frequency ionosphere-free model

5 结 论

基于BDS-3 和Galileo 多频信号，本文分析了具有低噪声和弱电离层延迟影响的整数线性组合特性，构建了基于弱电离层组合模型的中长基线RTK 定位模型，并与常规的双频无电离层组合模型进行了对比，也采用了实测的中长基线数据进行了验证。

组合观测值特性分析结果表明，BDS-3 存在4 个较优的弱电离层组合，其中以(2,2,-3,0,0)组合为最优；Galileo 存在3 个较优组合，以(4,-2,0,-1,0)组合为最优。最优的弱电离层组合观测量以周为单位和以距离为单位的电离层延迟影响系数均接近于0，基本不受电离层延迟的影响，与双频无电离层组合具有相当的波长，并具有更小的噪声。实测的中长基线数据实验表明，弱电离层组合由于无需解算宽巷模糊度，相比双频无电离层组合模型具有更多的可搜索窄巷模糊度数量；模糊度解算的模型强度和首次固定速度均优于双频无电离层组合，在定位精度上也分别提升了17.4% (N)、10.9% (E)和19.7% (U)。

总的来说，在定位参数解算性能上，弱电离层组合略优于双频无电离层组合；在解算流程和复杂性上，多频弱电离层组合模型无需解算宽巷模糊度，解算流程更简单，且每颗卫星仅需播发各一个组合后的载波和伪距观测值，因此差分数据量能够大幅减少，因此能以较小的数据传输量应用于中长基线RTK 定位中。