论数学建模在高职数学教学中的重要性
2020-04-03袁娜,杨梅
袁 娜,杨 梅
(重庆电子工程职业学院,重庆 401331)
我国在80年代初将数学建模引入了课堂,1992年由中国工业与应用数学学会组织举办了我国10个城市的大学生数学建模比赛,1999年,全国大学生数学建模竞赛设立了专科组。高职学生的数学基础比较薄弱,导致学生在学习的过程中容易情绪化,积极学习感兴趣的内容,消极对待枯燥乏味的学习内容。由此使得传统形式的课堂理论教学难以激发学生的学习兴趣。数学建模可以培养学生应用数学知识解决实际问题的能力,进一步提高解决专业技术问题的能力,从而促进学生良好成长和发展。
1 充分认识和了解数学建模
数学建模是建立数学模型的简称,是一种以数学思维思考的方式,是运用数学原理、方法、语言,通过简化建立接近并能够解决实际问题的一种有力的数学方式。通过开展数学建模,把数学的语言应用到实际问题中,而实际问题的对模型分析的特殊需求又往往对数学的理论提出新的挑战。数学建模不但要求学生与建模过程中的各个因素建立联系,如提出数学建模问题、测量数据、建立模型,还要求学生把自身掌握的数学知识和已有经验相联系,进而求解数学模型,检验数学模型的解。因此,对高职院校的学生而言,只有让他们看到了数学与专业、行业以及日常生活的广泛联系,体会到了数学的应用价值,才会增强学习的自觉性和主动性。
2 数学建模可以促进工科数学的教学改革
数学建模是连接数学理论与现实问题的桥梁和纽带。把数学建模思想融入工科数学教学中,数学建模的过程就是应用数学理论和数学方法分析并解决实际问题的过程,改
革传统教育模式,有利于培养学生对数学知识的应用能力。将数学建模的思想与方法从竞赛场引入到高等数学课堂,在数学教学中融入专业的思想与数学建模的方法,针对专业的实际应用和职业岗位能力需要,对高等数学教学方法与手段进行大胆改革,从根本上改变工科高等数学教学与行业、专业和实际生活相脱节的现象。
3 数学建模可以培养学生用数学方法分析解决实际问题和使用计算机的能力
就目前高职数学的现状而言,一方面,高职院校中高等数学教学普遍存在内容多、课时少的问题,教师在教学中往往只注重理论知识的教学,忽视了知识的应用和学科之间的结合,这样使学生体会不到数学的真正用处。另一方面,随着90年代末我国大力发展高等教育,不断扩招导致高职学生数学基础在不断下降,现在的高职学生思维以直观思维为主,因此,在教学过程中,应以直观教学法为主,通过巧设教学情境、数形结合、计算机辅助等方式,让学生积极参与问题的解决与模型建立的过程,激发学生的学习热情,提高其学习能力、建模能力,培养其创新精神,可以充分体现出以教师为主导、学生为主体的教学效果。数学建模因其具有独特的思维的灵活性和结论的不确定性,所以在解决实际问题时可以从不同的角度,采用不同的数学方法建立数学模型,激发学生的想象力、观察力和创造力;在建模时往往需要查阅相关文献资料,从中吸取有用的信息用于建模,这无形之中拓宽了学生的知识面,培养了学生的科研能力;在求解模型时,因数学模型计算的复杂和多样性,需要用Matlab、Lingo、Excel等计算软件处理,对Matlab则重点介绍其在数学计算、图形描绘等方面的操作,培养学生计算机软件的学习和应用能力;对Lingo软件,主要介绍它求解线性问题、非线性问题和整数规划问题的操作;对Excel软件,主要介绍其在数值计算、数据统计分析与图表生成方面的操作。
4 把数学建模融入高职数学教学的案例分析
以我校经管类专业学生的数学教学为例,用数学建模来解决经营中的最低费用问题。
设有n种食物,各含m种营养素,第j种食物中第i种营养素的含量为aij,n种食物介格分别为c1,c2,c3,… ,cn,请确定食谱中n种食物的数量x1,x2,x3,… ,xn,要求在食谱中m种营养素的含量分别不低于b1,b2,b3,… ,bn的情况下,使得总费用最低。
4.1 模型假设
在食谱的制作过程中,食谱的费用与食谱中各食物的价格、食物中各营养素含量是相互影响的。所以食谱制作商在保证产品各种营养素含量的同时,只有选择合适的食物数量,才能使得总费用最低。在此忽略通货膨胀等外界因素造成的影响。
4.2 模型建立
根据食物数量及价格可写出食谱费用为

其次食谱中第i种营养素的含量为
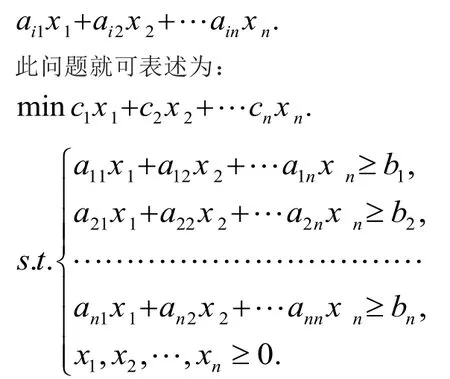
4.3 模型求解
利用Lingo软件实现模型求解:
MODEL:
SET:
ad/1..5/:c,x;cf/1..6/:b;
links(ad,cf):a;ENDSETS
DATA:B=4,5,3,3,5,4;
a=1,2,1,1,0,1 0,5,0.4,0.2,1,1,1 1,0.2,0.8,0,2,1 1.5,1.2,0,0.9,0.3,1 1,0.5,1.5,0,1.5,0.5;
c=1,2,3,4,5;ENDDATA MIN=@SUM(ad:c*x);
@FOR(cf(j):@SUM(ad(i):a(I,j)*x(i))>=b(j););
END
求解结果:10.05882
5 总结
在高职学院的数学教学中,我们不是仅仅将学生培养成只会计算或只懂理论知识的被动学习者,将数学建模渗透进课堂,才能调动学生学习的主观能动性,才能更大范围地提高学生数学应用能力和创新能力,为社会培养具有较高能力的复合型、应用型人才。
