基于卷积神经网络的多聚脯氨酸二型二级结构预测
2020-04-02刘阳,孟艾
刘 阳,孟 艾
(山东理工大学计算机科学与技术学院,山东 淄博 255049)
0 引 言
多聚脯氨酸二型螺旋(polyproline type II helix)与常规蛋白质二级结构α螺旋和β折叠不同,它的长度大致分布在3~8之间,且在蛋白质中非常稀少,约占2%。而目前,PPII(polyproline type II)螺旋已被PROSS[1]、XTLSSTR[2]、SEGNO[3]、DSSP-PPII[4]和ASSP[5]程序注释为独立的蛋白质二级结构。
PPII螺旋在许多生物化学过程中扮演着非常重要的角色。由于许多转录因子的末端都富含脯氨酸,因此PPII螺旋在转录过程中起到重要的作用[6]。PPII螺旋在信号传导、细胞运动以及免疫反应等过程中起着至关重要的作用[7]。PPII螺旋与蛋白质或核酸存在着许多相互作用,如SH3结构域与PPII螺旋结合产生的相互作用[8]。PPII螺旋与很多疑难疾病有关,例如PPII螺旋在阿尔茨海默病和帕金森病中的潜在作用[9-10]。
目前蛋白质结构数据库PDB[11]中所存储的蛋白质结构数据主要通过X射线晶体衍射等成像技术得到,而通过蛋白质序列数据来预测PPII螺旋极大地降低了识别的成本和时间,为研究蛋白质的功能和相互作用提供帮助。
尽管目前对常规二级结构的预测研究非常多,但对PPII螺旋预测的研究工作相对非常少,且处于初步阶段。由于PPII螺旋非常稀少,预测PPII螺旋相比预测其它常规二级结构更加困难。并且之前的研究表示蛋白质序列的特征编码方法较为单一,主要使用对蛋白质序列窗口化和氨基酸直接编码的方法[12-15]。对于PPII螺旋预测使用到的算法仅有人工神经网络[12,16]、支持向量机[13-14]和遗传神经网络[15]这3种传统机器学习算法。最初由Siermala等人[12]使用人工神经网络模型实现了对PPII螺旋的预测,人工神经网络模型结构包括输入层、单个隐藏层和输出层,其中输入层的输入为13个氨基酸正交码组成的一维特征向量,隐藏层的节点个数为4,输出层的输出为单个氨基酸残基是PPII螺旋的概率值。Siermala等人[12]使用人工神经网络模型,在测试集正负样本不平衡的情况下,经测试,准确率达到约73%。Wang等人[13]提出一种基于支持向量机的预测算法,进一步减少了同源蛋白质序列,达到了70%的准确度。之后陆克中等人利用支持向量机[14]、遗传神经网络[15]和改进编码的人工神经网络[16]实现对PPII螺旋的预测,其中支持向量机[14]优于遗传神经网络[15]和改进编码的人工神经网络[16],准确度约为76%。
自2006年Hinton等人提出了深度学习的概念以来,掀起了一波国内外的研究热潮,学者们对其不断研究和探索,并衍生出了多种深度学习模型。相比于多层感知器,深度学习模型的隐藏层的数量和模型参数更多,隐藏层的结构更加复杂。其中卷积神经网络与全连接的多层感知器不同,卷积神经网络利用卷积层自动提取局部特征,并大大减少了网络权重数量。卷积神经网络已成功应用到目标检测[17]、生物信息识别[18]、自然语言处理[19]等多个领域和场景之中,也包括蛋白质结构的预测[20]、蛋白质结合位点的预测[21]等。因此本文提出一种基于卷积神经网络的PPII螺旋预测算法,并与6种传统机器学习算法进行了比较。
1 数据集与特征编码
1.1 数据收集
从PolyprOnline[22]数据库下载蛋白质序列信息和DSSP-PPII[4]方法注释的PPII螺旋信息,其中DSSP-PPII[4]与目前使用最广泛的二级结构注释程序DSSP[23]相匹配,这对PPII螺旋的预测是十分有利的。从下载的全部蛋白质序列中筛选长度大于40,分辨率小于3.0 Å,且包含连续3个残基组成的PPII螺旋的蛋白质序列,并通过CD-HIT[24]程序去除相似度大于30%的冗余序列,最终获得6647条蛋白质序列,其中包含38360个PPII螺旋残基和2044874个非PPII螺旋残基。
1.2 蛋白质序列特征编码
蛋白质序列特征编码方式包括21类氨基酸正交码(其中最后一位为未知氨基酸)、7类氨基酸物理化学性质和位置特异性计分矩阵(Position-Specific Scoring Matrices, PSSM)。其中7类氨基酸物理化学性质分别为疏水性、亲水性、等电点、PK1值、PK2值、空间参数和极化率。20维的PSSM矩阵由PSI-BLAST[25]程序比对NCBI的非冗余蛋白质数据库NR获得,e值设置为0.001,迭代次数设为3次。若使用以上全部3类特征,则单个氨基酸可以表示为维度为48的特征向量。
1.3 样本与数据集
若一条蛋白质序列的长度为L,使用滑动窗口在整条蛋白质上截取大小为2m+1的蛋白质序列片段表示单个氨基酸样本,则整条蛋白质序列样本个数为L。若滑动窗口大小为13,正样本(PPII螺旋残基)和负样本(非PPII螺旋残基)的截取如图1和图2所示。
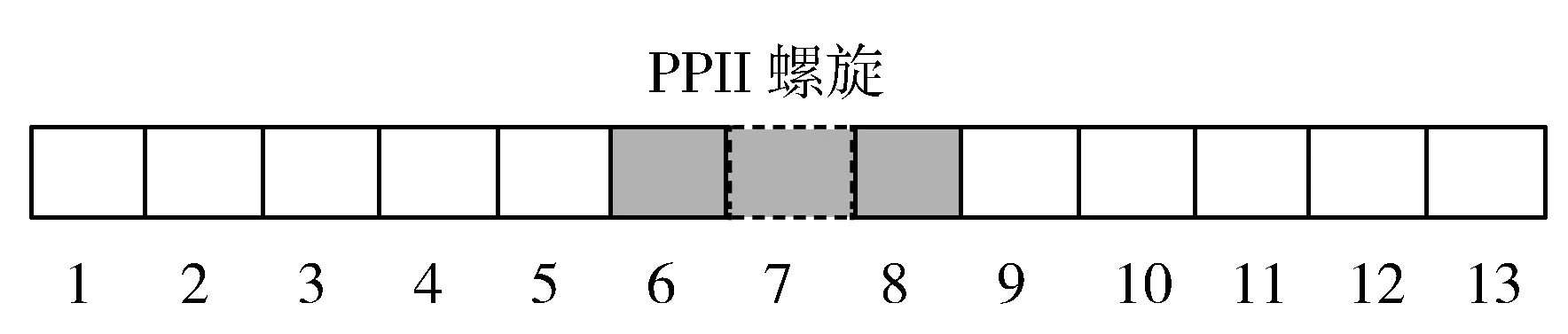
图1 正样本
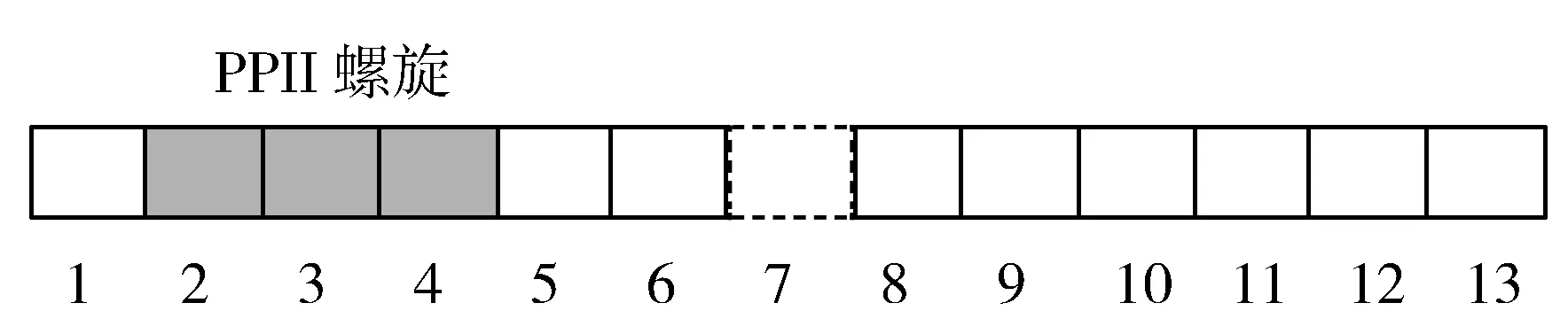
图2 负样本
从收集的6647条蛋白质序列随机选取5317条序列作为原始训练数据,剩下的1330条蛋白质序列的样本全部作为测试数据。样本分布如表1所示。
表1 样本分布

数据序列条数正样本个数负样本个数原始训练数据5317310671648263测试数据13307293396611
数据集分训练集、验证集和测试集。为解决原始训练数据正负样本的严重不平衡问题,使用欠采样的方法,在原始训练数据中随机抽取了与正样本等量的31067个负样本,和全部的正样本合并在一起成为训练数据。训练数据又分割为训练集和验证集,比例为4:1。测试数据的正负样本全部作为测试集。
2 卷积神经网络模型
卷积神经网络的结构主要由输入层、卷积层、平坦层、全连接层和输出层构成,如图3所示。
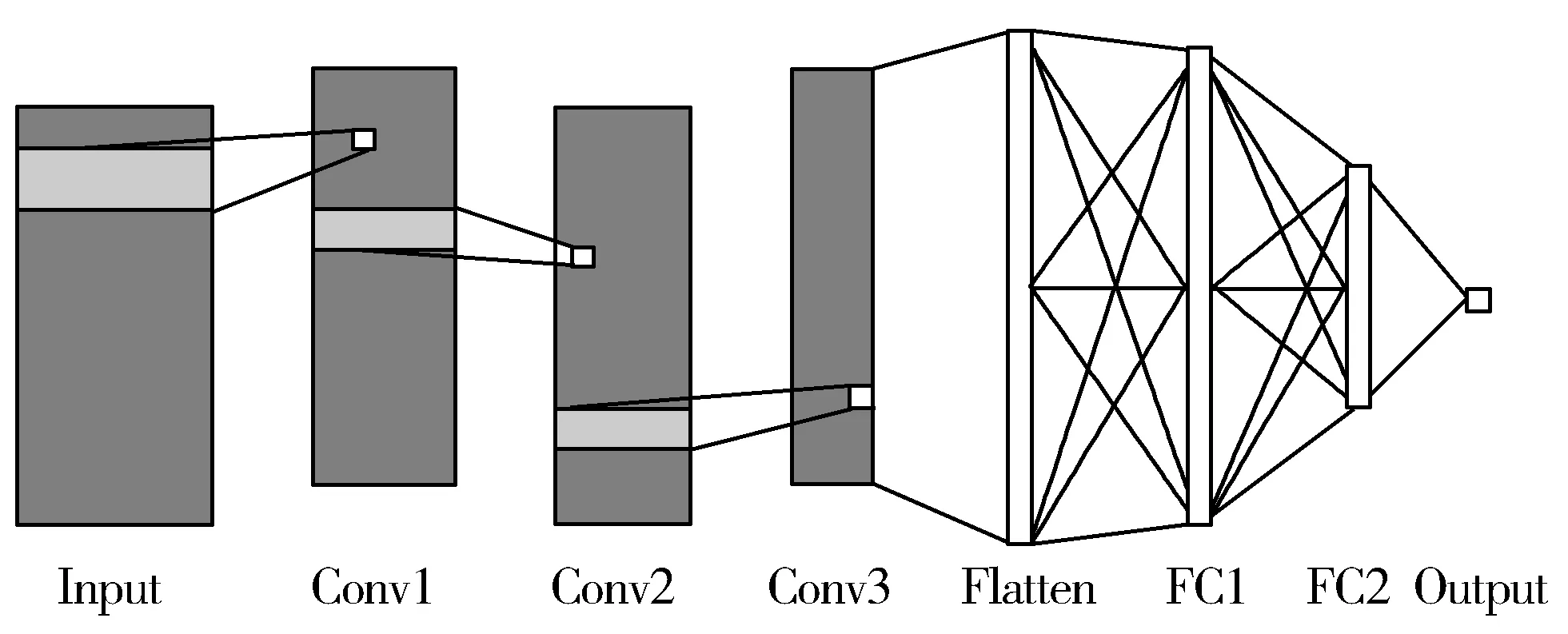
图3 卷积神经网络模型
输入层(Input)输入的是归一化处理之后单个样本的特征矩阵,若使用正交矩阵、氨基酸物理化学性质和位置特异性计分矩阵3类特征编码,滑动窗口大小为13,则输入到模型中单个样本的特征矩阵的尺寸为13×48。
在卷积层中,可把多个卷积核作为局部共享权重,对输入模型的13×48大小的二维特征矩阵进行一维卷积计算,生成多个含有深层特征的特征向量。
本文模型包含3个卷积层:
1)第一个卷积层(Conv1)的卷积核的个数为32,卷积核的长度为5,深度为48。通过卷积计算输出由32个长度13的特征向量组成的13×32大小的特征矩阵。
2)第二个卷积层(Conv2)的卷积核的个数为32,卷积核的长度为3,深度为32。输出13×32大小的特征矩阵。
3)第三个卷积层(Conv3)的卷积核的个数为16,卷积核的长度为3,深度为32。输出13×16大小的特征矩阵。
为了防止模型训练中出现过拟合,每一个卷积层之后都会经过正则化层(Batch Normalization)和丢失层(Dropout)处理,其中丢失层的丢失率为0.5。
多个卷积层处理之后的特征矩阵经过平坦层(Flatten)转换为一维的特征向量,输入到由2个全连接隐藏层组成的多层感知器中,第一层(FC1)的节点个数为128,第二层(FC2)的节点个数为32,且每一层都经过丢失层(Dropout)处理,丢失率为0.5。输出层(Output)通过激活函数Sigmoid输出PPII螺旋残基的概率值,其它层激活函数为Relu。
模型的损失函数设为二元交叉熵(binary-crossentropy),优化函数为Adam(Adaptive Moment Estimation)。模型的初始学习率设置为0.001,利用ReduceLROnPlateau自动减小学习率。设置模型训练时的batch_size大小为128,当验证集的损失值不再减小时,通过EarlyStopping自动结束训练过程。
3 实验方法与结果分析
3.1 实验环境
实验以Python3.6语言作为开发环境,以Keras平台框架作为工具构建深度学习网络模型,以Scikit-learn为工具构建传统机器学习模型。实验平台中央处理器为英特尔(Intel) Xeon E3-1225 v5,内存为8 GB,操作系统为Ubuntu 16.04,显卡为英伟达(NVIDIA) Quadro K620。
3.2 评估参数
对于PPII螺旋的预测是一种二分类问题,使用灵敏度(TPR)、特异度(SPC)、总精度(ACC)、ROC曲线下方的面积(AUC)和马修斯相关系数(MCC)来评估。ROC曲线的横坐标为假阳性率(FPR),纵坐标为真阳性率(TPR),表示阈值在0~1之间取值时假阳性率与真阳性率的曲线。ROC曲线下方面积为AUC,取值为[0,1],AUC值越接近1预测效果越好。MCC取值为[-1,1],MCC值越接近1预测效果越好。由于正负样本严重不均衡,会导致灵敏度和准确率相对较高,而使用AUC来评估相对准确。
3.3 不同特征组合下的实验
本文设计了由氨基酸正交码、氨基酸物理化学性质和位置特异性计分矩阵这3种编码方式,组合成了7种不同的特征组合的数据集:仅使用氨基酸正交码(OC);仅使用氨基酸物理化学性质(PhyChem);仅使用位置特异性计分矩阵(PSSM);正交码与氨基酸物理化学性质合并(OC_PhyChem);正交码与位置特异性计分矩阵合并(OC_ PSSM);氨基酸物理化学性质与位置特异性计分矩阵合并(PhyChem_PSSM);正交矩阵、氨基酸物理化学性质和位置特异性计分矩阵合并(OC_PhyChem_PSSM)。
使用7种不同特征组合的数据集的训练数据,训练本文构建的卷积神经网络模型。训练结束后的模型在测试集上的评估结果如表2所示。
表2 不同特征组合方式在测试集上的评估结果
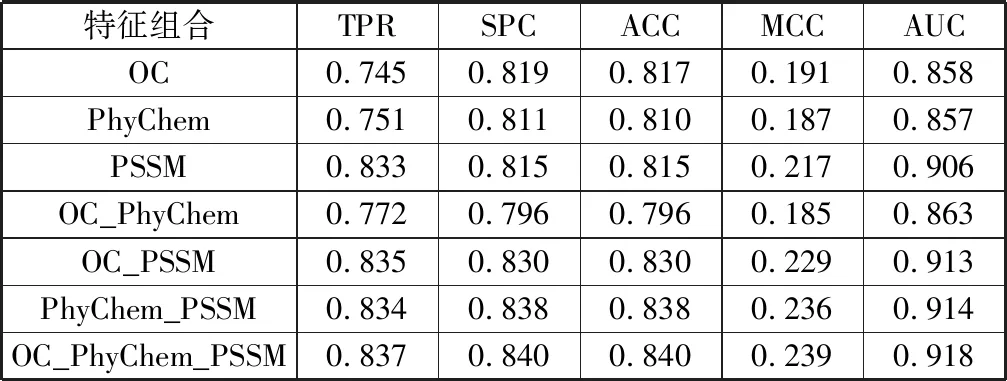
特征组合TPRSPCACCMCCAUCOC0.7450.8190.8170.1910.858PhyChem0.7510.8110.8100.1870.857PSSM0.8330.8150.8150.2170.906OC_PhyChem0.7720.7960.7960.1850.863OC_PSSM0.8350.8300.8300.2290.913PhyChem_PSSM0.8340.8380.8380.2360.914OC_PhyChem_PSSM0.8370.8400.8400.2390.918
从表2可以看出,在仅使用一种蛋白质序列特征编码的情况下位置特异性计分矩阵的评估结果相比于氨基酸正交码和氨基酸物理化学性质有着明显优势。相较于仅使用一种蛋白质序列特征编码的氨基酸正交码,特征中加入位置特异性计分矩阵对于评估结果的提升较大,例如OC_PSSM的AUC值比OC提高了近0.055。而使用全部3种蛋白质序列特征编码的OC_PhyChem_PSSM的评估结果比其他特征组合方法相对较好,马修斯相关系数为0.239,AUC值为0.918。
3.4 不同滑动窗口大小下的实验
为了寻找最优的滑动窗口大小,窗口大小以2为步长,从5到21,在测试集上的评估结果如表3所示。
表3 不同窗口大小在测试集上的评估结果
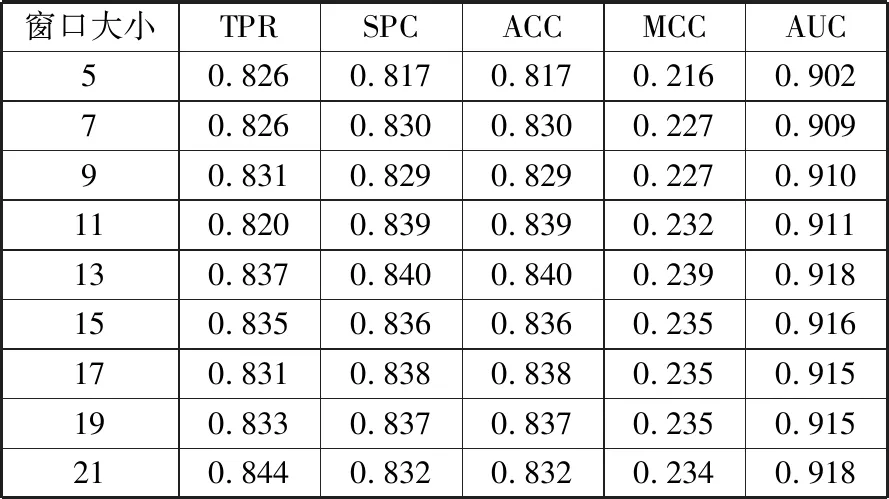
窗口大小TPRSPCACCMCCAUC50.8260.8170.8170.2160.90270.8260.8300.8300.2270.90990.8310.8290.8290.2270.910110.8200.8390.8390.2320.911130.8370.8400.8400.2390.918150.8350.8360.8360.2350.916170.8310.8380.8380.2350.915190.8330.8370.8370.2350.915210.8440.8320.8320.2340.918
从表3可以看出,当窗口大小为5时,评估结果相对较差,经窗口大小调大,评估结果有了明显提升,而当窗口大小为13时的评估结果相对优秀,AUC值为0.918,因此,本文最终把窗口大小定为13。
3.5 丢失率的选取
为了防止卷积神经网络模型出现过拟合现象,寻找较好的丢失层(Dropout)的丢失率,设计了不同数值的丢失率,在测试集上的评估结果如表4所示。
表4 不同丢失率在测试集上的评估结果
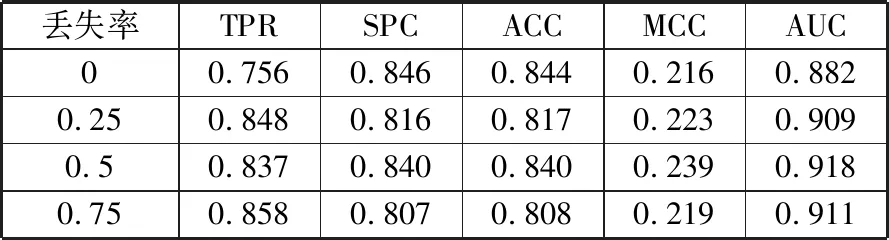
丢失率TPRSPCACCMCCAUC00.7560.8460.8440.2160.8820.250.8480.8160.8170.2230.9090.50.8370.8400.8400.2390.9180.750.8580.8070.8080.2190.911
从表4可以看出,当丢失率为0时,相当于没有添加丢失层,AUC值相对较低,而通过添加丢失层,AUC值有所提升。而丢失率为0.5时AUC值相对较好,因此,本文最终把丢失率定为0.5。
3.6 池化层的选取
卷积神经网络的隐藏层除了卷积层之外,也经常使用池化层来减少模型的参数,防止过拟合。而一维的池化操作缩减了特征矩阵的长度,而特征矩阵的特征维度不变。然而蛋白质序列经过特征编码生成的特征矩阵是由多个氨基酸编码的特征向量组成,并且氨基酸编码的特征向量之间有着固定的排列顺序。所以由蛋白质序列生成的特征矩阵进行一维池化操作,在一定程度上丢失了氨基酸的相对位置信息。因此,本文对是否应该在模型中添加池化层进行讨论,并设计了4组实验:不添加最大池化层;仅第三卷积层(Conv3)之后添加最大池化层;第三卷积层(Conv3)和第二卷积层(Conv2)之后添加最大池化层;3个卷积层之后全都添加最大池化层。其中最大池化层的pool_size大小为2。4种池化层添加方法在测试集上的评估结果如表5所示。
表5 4种池化层添加方法在测试集上的评估结果
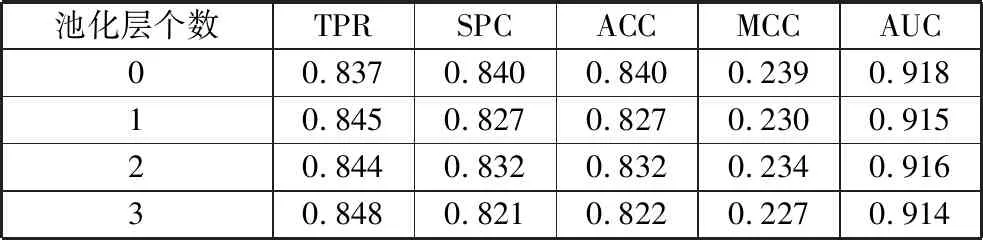
池化层个数TPRSPCACCMCCAUC00.8370.8400.8400.2390.91810.8450.8270.8270.2300.91520.8440.8320.8320.2340.91630.8480.8210.8220.2270.914
实验结果表明模型中添加池化层在预测性能上并没有提升,所以本文模型不添加池化层。
3.7 与传统机器学习方法的比较
为了表明本文方法的优越性能,选择了6种传统机器学习方法与本文方法相比较,包括逻辑回归(LR)、线性判别分析(LDA)、梯度提升决策树(GBDT)、支持向量机(SVM)、多层感知器(MLP)和随机森林(RF)。其中多层感知器的隐藏层层数为1,隐藏层节点个数为16。在测试集上的评估结果如表6所示,ROC曲线如图4所示。
表6 本文方法与传统机器学习方法在测试集上的评估结果
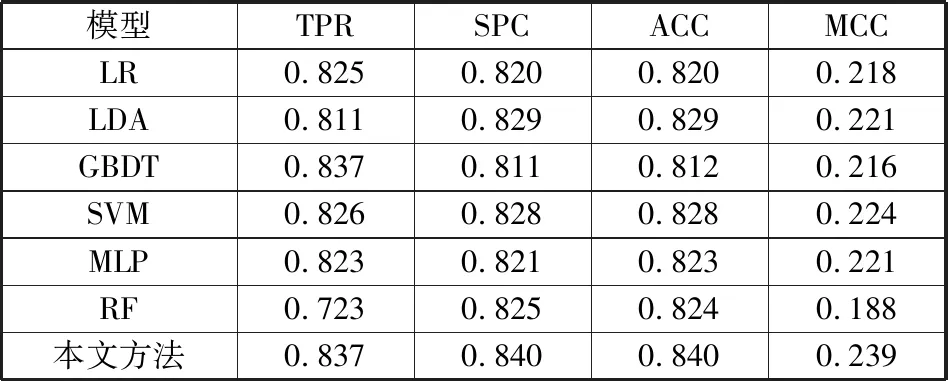
模型TPRSPCACCMCCLR0.8250.8200.8200.218LDA0.8110.8290.8290.221GBDT0.8370.8110.8120.216SVM0.8260.8280.8280.224MLP0.8230.8210.8230.221RF0.7230.8250.8240.188本文方法0.8370.8400.8400.239
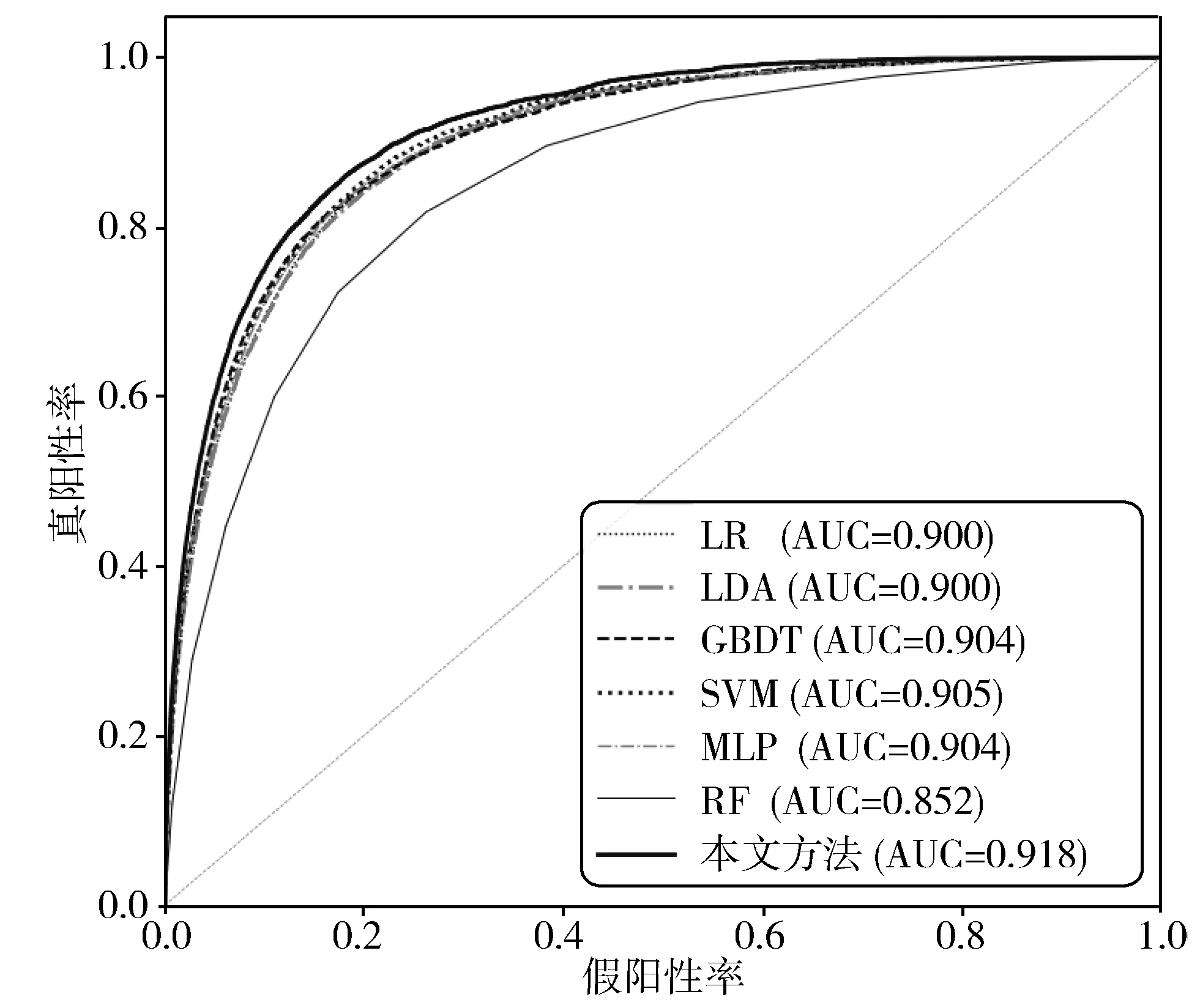
图4 本文方法与传统机器学习方法在测试集上的ROC曲线
4 结束语
基于卷积神经网络的深度学习算法对于预测多聚脯氨酸二型螺旋具有较好的性能,在测试集上准确度(ACC)达到84.0%,马修斯相关系数(MCC)为0.239,感受性曲线下的面积(AUC)为0.918。在特征组合中加入位置特异性计分矩阵(PSSM)对于PPII螺旋的预测的性能提升较大。而且由于正负样本严重不均衡,使用欠采样的方法来组成训练集,丢失了大量的负样本,会使模型出现过拟合问题,这还有待改进。
