基于循环寻优RRT算法的无人机航迹规划
2020-04-02肖支才尹高扬
肖支才,尹高扬,闫 实
(海军航空大学,山东 烟台 264001)
0 引 言
随着无人机在现代战争中的广泛使用和优异表现,无人机所处的战场环境越来越复杂,执行的任务也越来越多元化[1]。分布式多无人机协同作战成为无人机作战运用的重要发展趋势[2]。多无人机的协同任务时间是通过综合机群中各无人机的预计达到任务点的时间得到,需要各无人机具有在线自主航迹规划功能,对航迹规划的实时性要求较高[3]。单无人机航迹规划不仅需要考虑威胁区、障碍区等已知威胁,还需要综合考虑协同到达时间、无人机自身的动力学约束和燃油、可执行任务等约束。单无人机在线自主航迹规划需要在满足各种复杂约束的条件下对规划航迹的快速可行性和最优性进行折中处理。
传统的航迹规划方法是将约束条件融入到代价函数之中,搜索产生一条代价最小的可行路径。求解的搜索算法主要分为确定性算法[4-6]和智能优化算法[7-14]2大类。由于无人机航迹规划的规划区域广阔,同时航迹规划是一个NP问题[15]。确定性算法和智能优化算法要获得一条最优或较优航迹,需要较长的收敛时间和极大的内存需求,无法满足无人机在线自主航迹规划的快速性要求。
快速扩展随机树(RRT)方法是一种基于采样的单查询随机搜索算法[16],在节点扩展时能够根据规划区信息快速有效地搜索规划空间,在可行路径的搜索概率意义上是完全的。RRT方法能够满足单无人机在线自主航迹规划的快速性要求,但是由于节点扩展的随机性,RRT方法只能快速获得可行航迹,无法获得较优航迹。针对RRT方法的不足,研究者们从RRT方法的节点采样方式、节点选择方式和节点扩展方式3个方面对其进行改进,取得了一定的成果[17-21],但是所生成航迹的航迹长度代价离最小航迹长度代价还有一定的差距。航迹长度代价约束作为启发条件引入到快速扩展随机树(RRT)算法中,可以有效地剪除搜索空间的无用节点,获得较优航迹[22]。航迹长度代价的选取一般根据无人机的最大可飞行航程和无人机协同任务的预定飞行时间。无人机的最大可飞行航程容易满足,而无人机协同时间的确定基于单无人机在线自主航迹规划得到的时间,航迹长度代价约束在获取较优航迹时没有得到充分利用。
本文提出一种循环寻优RRT方法,对基本RRT方法的改进成果都可以被采用,运行得到的较优解都会得到保留。较优解的航迹长度代价作为算法下一次运行的启发信息,确保了新生成航迹的长度代价都优于上一次算法运行生成的航迹。通过算法循环运行,使得最终得到的航迹趋近于最优航迹的最小航迹长度代价。同时,算法能够得到一系列不同航迹长度代价的备用可行航迹,在协同任务中可以根据协同到达时间进行快速选择。
1 RRT方法及其改进方法
基于RRT方法的航迹规划将规划空间中的规划起始点为根节点,通过随机采样逐渐增加叶节点的方式生成随机扩展树。当随机树的叶节点中包含了目标点或者目标区域的点时,随机树停止扩展,此时可以在随机树中找到一条以根节点组成的从起始点到目标点的路径。RRT的节点扩展方式如图1所示。
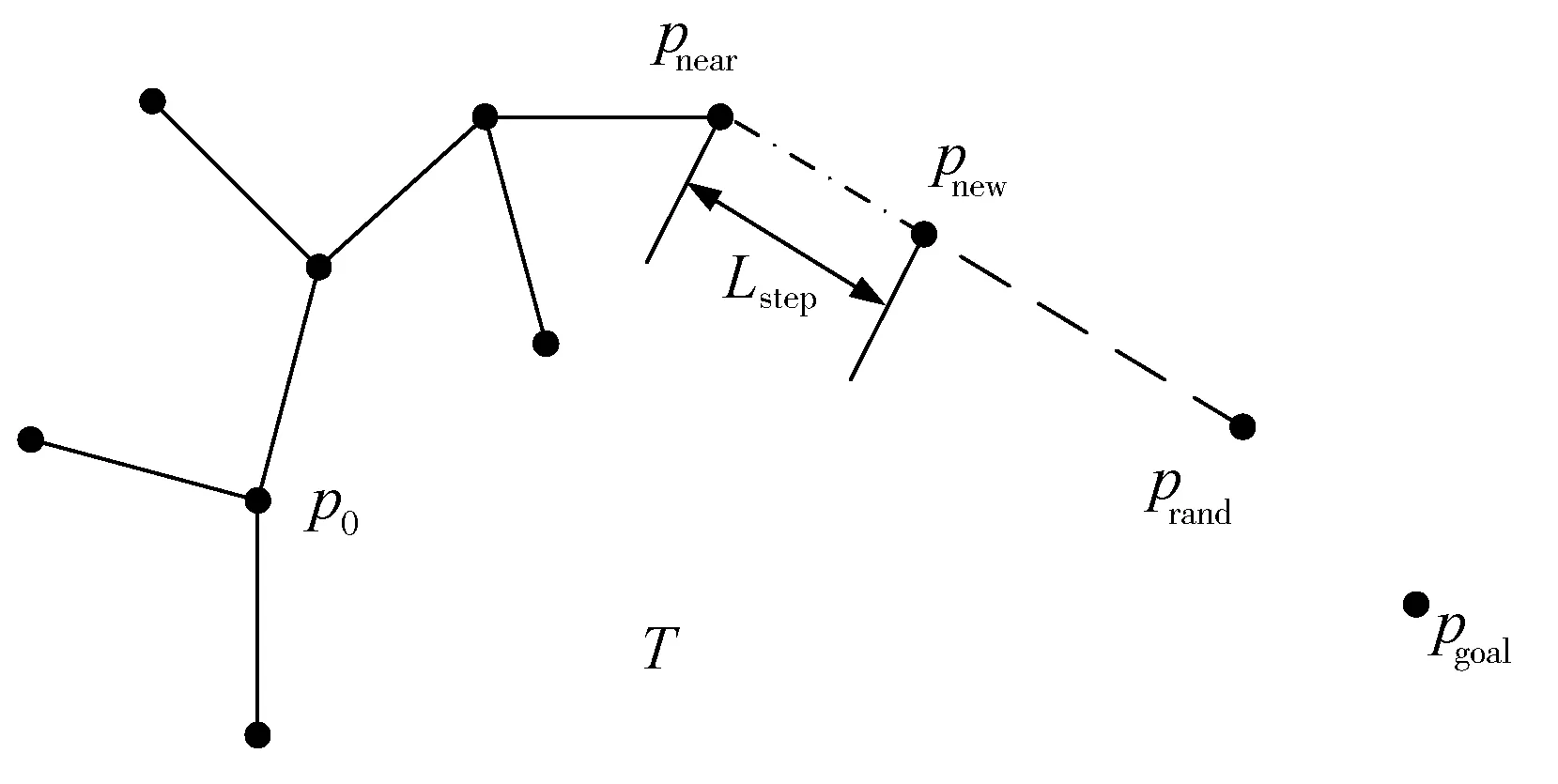
图1 基本RRT算法的扩展过程
图1中T表示当前存在的扩展树,prand表示规划空间中的随机采样点,pnear表示已有扩展树上离随机采样点prand距离最短的一个树节点。在prand和pnear的直线连线上以扩展步长Lstep为单位截取得到新扩展节点pnew,在向新扩展节点pnew行进的过程中如果没有碰到障碍物或者威胁,则将pnew加入到扩展树中,否则需要重新选择为随机采样点prand。继续迭代运算,直到pnew到达目标区域则算法结束,此时可以在扩展树T中找到一条从起点p0到目标点pgoal的航迹。
文献[17]在确定已有扩展树上离随机采样点prand距离最短的一个树节点pnear时,采用多重选取pnear策略,通过评价函数选择最优pnear;文献[18]采用多重随机采样策略,通过评价函数选择最优随机采样点prand;文献[19]在随机采样点选取中,引入了导航点缓存策略,以一定概率选择缓存导航点作为目标点进行扩展,引导扩展树朝较优航迹方向生长。
2 循环寻优RRT方法
2.1 航迹长度代价约束
航迹长度代价约束是剪除规划空间中的无用节点,引导航迹长度代价趋向于最短航迹的策略。航迹长度代价为已规划的从起始点到目标点的可行航迹的长度dcost。
令已规划的可行航迹为航路点集合{p0,p1,…,pgoal},p0为航迹规划的起点,pgoal为目标点,则:
(1)
节点扩展过程中,从规划起始点到新扩展节点的距离与新扩展节点到目标点之间的直线距离之和如果大于这个距离,此新节点为无效点,即使满足其他约束条件也不能加入到已有扩展树T中。
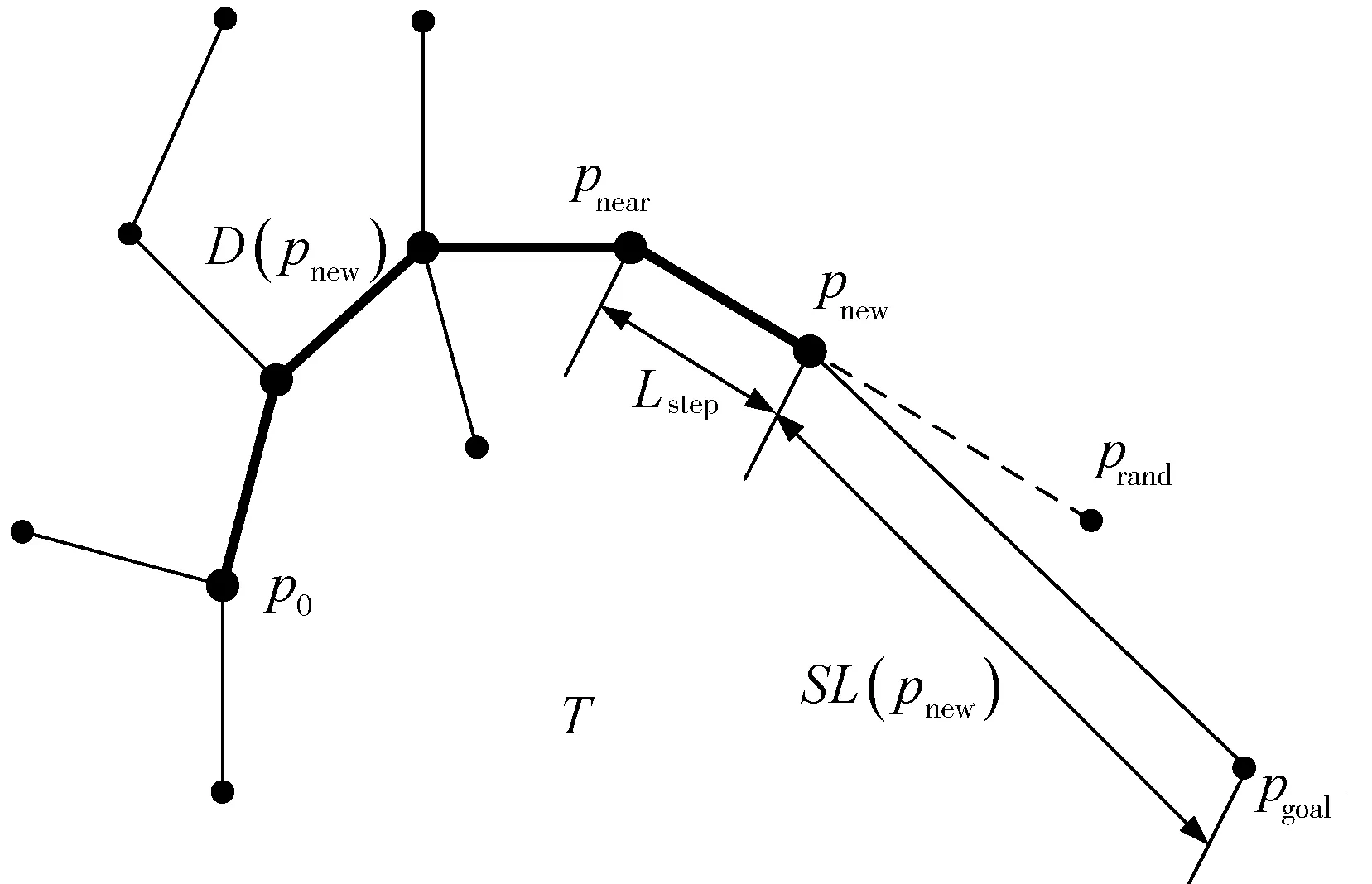
图2 航迹长度代价约束
航迹长度代价约束在二维空间的投影表示如图2所示。新的扩展节点pnew,通过追溯根节点得到从起始点到pnew的航迹距离为D(pnew),即图中黑色粗实线航迹。
(2)
SL(pnew)是从扩展节点pnew到目标点pgoal的欧氏距离。
SL(pnew)=pnewpgoal
(3)
航迹长度代价约束条件为:
D(pnew)+SL(pnew)dcost
(4)
pnew只有满足不等式(4)时,才能把它加入到已有的扩展树T中。在循环寻优RRT方法的第一次循环时,可以根据无人机的燃料载荷和任务执行时间的限制来设定dcost的值。为了兼顾算法的快速性和寻优性,在每次循环中,如果节点扩展数大于100个,扩展树仍未获得优于当前航迹长度代价的航迹,则退出当前循环,保留当前航迹长度代价和对应航迹点进入下一次循环。
2.2 无人机动力学约束条件
无人机受自身动力学影响,航迹规划算法生成的可飞行航迹必须满足以下约束[23]:
1)无人机的最小航迹段长度约束。根据无人机的导航要求和机动能力,在无人机开始改变其飞行姿态之前要求保持直线飞行的最短距离。
2)无人机的最大拐弯角。无人机受自身可承受过载和平面机动能力的影响在改变航向时受到的角度约束。
循环迭代RRT算法将无人机的动力学约束融入到节点扩展的过程中,扩展树中2个节点之间的距离大于或者等于无人机的最小航迹段长度。通过计算新节点、离新节点距离最近的树节点和该树节点的父节点之间的夹角,确定新节点是否满足无人机的最大拐弯角约束。由于算法产生的是一系列航路点,无人机无法按照折线飞行,本文采用三阶B样条曲线对航路点连线进行平滑处理,生成无人机可飞行的航迹。
2.3 算法描述
基于循环寻优RRT方法的无人机航迹规划算法的具体步骤如下:
Step1以无人机的当前位置作为规划起始点p0。设定无人机的最小转弯角φ,初始化搜索树T。算法循环迭代次数N,最大新扩展节点数Nset。
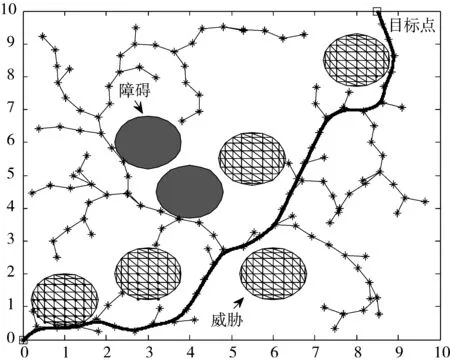
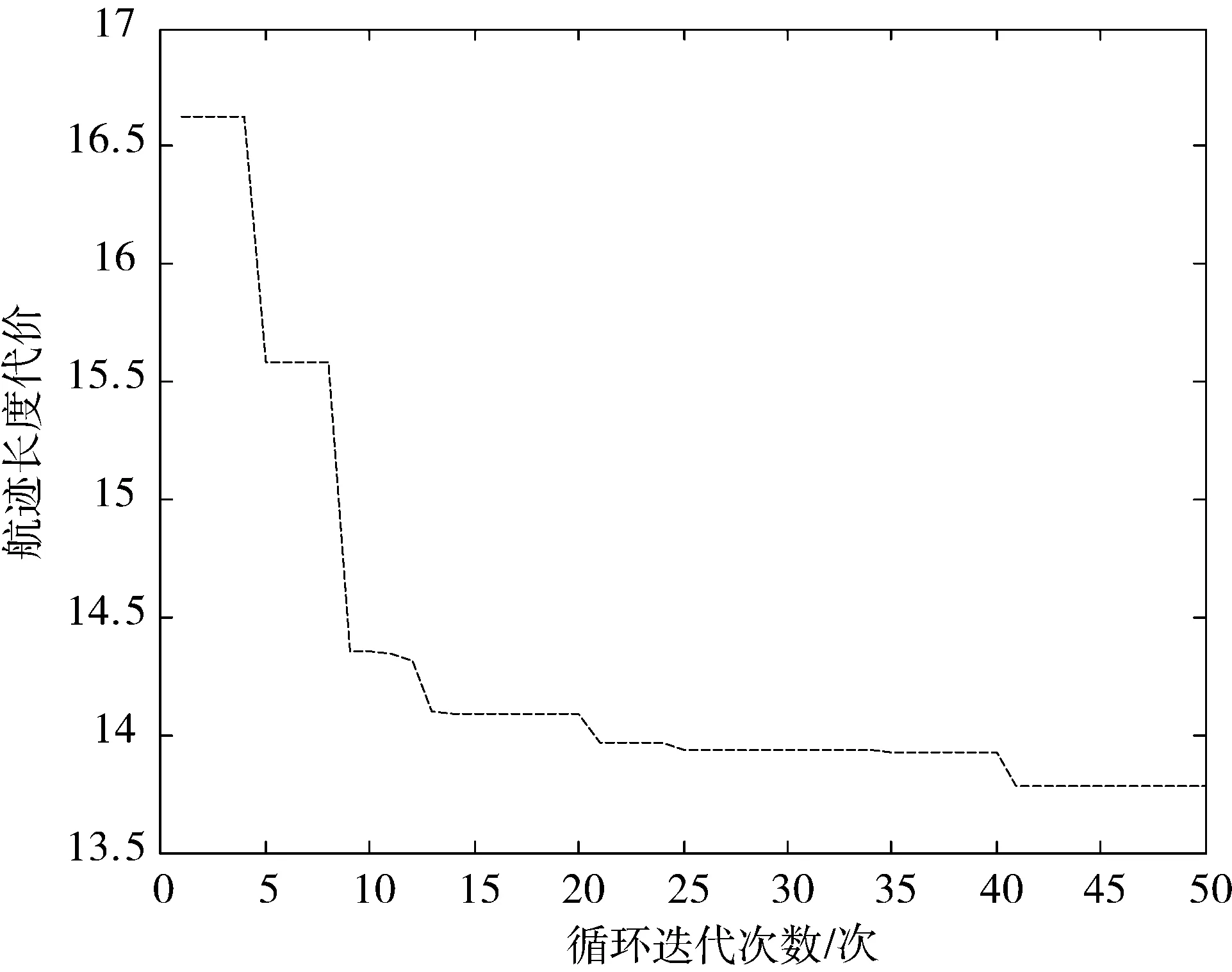
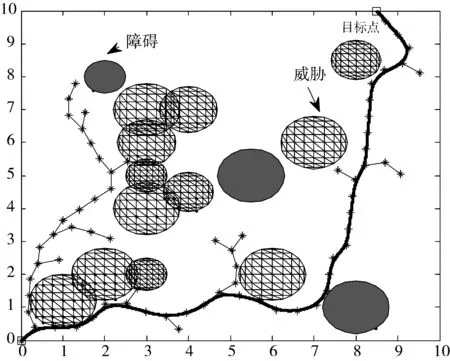
Step2产生随机数q∈[0,1],如果q Step3通过随机采样点prand,得到扩展树T的树节点p中离随机采样点和起始点p0距离最近的一个树节点pnear,使得Dis(pnear,prand)与Dis(pnear,p0)之和小于等于Dis(p,prand)与Dis(p,p0)之和。在pnear和prand的连线上,计算从pnear以最小航迹段长度L到达的新扩展点pnew。 Step4判断pnew是否满足障碍威胁规避、文中所述无人机动力学约束以及航迹长度代价约束。若满足,则将pnew加入到扩展树T中。否则转到Step2。 Step5对新扩展节点进行计数,当新扩展节点数小于设定值Nset,判断|pnew-pgoal|L,若满足,转到Step6,否则转到Step2。当新扩展节点数大于设定值Nset,本次算法循环结束。判断算法循环次数是否达到设定值N,若达到,保留上一循环航迹长度,生成航迹数据转入Step8。否则保留上一循环航迹长度,生成航迹数据转入Step2。 Step6通过形成的扩展树T,获得从起始点p0到终点pgoal的航迹,得到航迹长度S。 Step7判断算法循环次数是否达到设定值N,若达到,转入Step8。否则将航迹长度S作为启发条件进入算法下一次运行,转入Step2。 Step8采用三次B样条曲线对航迹进行平滑,得到最终航迹。 基于上述算法设计,在Intel 2.5 GHz主频,8 GB内存的普通PC机上使用MATLAB编程进行算法仿真实验。任务区域范围为10×10,存在的障碍物和威胁分别以实心圆和空心网格圆表示,规划起始点坐标为(0,0),目标点坐标为(8.5,10)。设定无人机的最大转弯角为60°,最小航迹段长度为0.5(无量纲),算法循环迭代次数为50次,最大新扩展节点数为100个,将目标点作为随机采样点的概率goalpro为50%。分别在7个和15个障碍物和威胁存在的战场态势下对RRT算法、RRT改进算法与循环寻优RRT方法进行仿真实验。 图3、图4和图5分别为RRT方法、文献[17]的hRRT方法和循环寻优RRT方法的单次仿真结果,图6为循环寻优RRT方法得到的航迹长度代价随迭代次数的收敛曲线。 图3 基本RRT方法的规划结果(7个障碍物和威胁) 图4 hRRT方法的规划结果(7个障碍物和威胁) 图5 循环寻优RRT方法的规划结果(7个障碍物和威胁) 图6 航迹长度代价的收敛曲线(7个障碍物和威胁) 在相同的仿真条件下,分别用RRT方法、hRRT方法和本文的循环寻优RRT方法进行100次实验,仿真结果如表1所示。 表1 算法效率对比表(7个障碍物和威胁) 100次实验RRThRRT循环寻优RRT平均航迹长度16.631714.934613.7245平均扩展节点111102100 由图5、图6和表1可知,循环寻优RRT方法规划出来的航迹距离要优于RRT方法和hRRT方法,同时循环寻优RRT方法可以得到航迹长度代价分别为16.63、15.52、14.41和13.78等的一系列备用可飞行航迹。 图7 基本RRT方法的规划结果(15个障碍物和威胁) 图8 hRRT方法的规划结果(15个障碍物和威胁) 图9 循环寻优RRT方法的规划结果(15个障碍物和威胁) 图10 航迹长度代价的收敛曲线(15个障碍物和威胁) 在相同的仿真条件下,分别用RRT方法、hRRT方法和本文的循环寻优RRT方法进行100次实验,仿真结果如表2所示。 表2 算法效率对比表(15个障碍物和威胁) 100次实验RRThRRT循环寻优RRT平均航迹长度16.538115.440714.2106平均扩展节点122109100 由图9、图10和表2可知,循环寻优RRT方法在简单和复杂战场态势下规划出来的航迹距离都要优于基本RRT方法和hRRT方法。将RRT算法及其改进方法的可行航迹的航迹长度代价约束作为启发信息代入到算法的下一次循环当中,加强了搜索过程中的启发信息,有效剪除了规划空间中的无用节点,搜索树将沿着航迹长度代价更小的近似最优航迹的方向进行扩展。设定的最大新扩展节点数,使得算法在无法快速获得小于当前最优航迹代价的航迹时退出当前循环。通过设定合理的循环次数和最大新扩展节点数,可以满足算法的快速性要求。算法能够得到一系列不同航迹长度代价的备用可行航迹,在协同任务中可以根据协同到达时间进行快速选择。 实验结果表明,基于循环寻优RRT方法的无人机航迹规划算法可以快速规划出满足无人机动力学约束等综合约束的可行较优航迹。 本文通过循环引入航迹长度代价约束到RRT算法中,提出了基于循环寻优RRT方法的航迹规划算法,解决了RRT算法及其改进算法在无人机在线自主航迹规划时,得到的航迹长度代价具有随机性,无法确保较小航迹长度代价的问题,同时获得了一系列不同航迹长度代价的可行备选航迹,便于无人机执行协同任务时根据协同达到时间进行快速选择。最大新节点扩展数和循环迭代次数的设定,保证了单次循环和整体规划的快速性,兼顾了航迹规划的寻优性与实时性。仿真结果验证了所提方法的有效性。3 仿真结果及分析
3.1 7个障碍物和威胁存在的战场态势下仿真结果

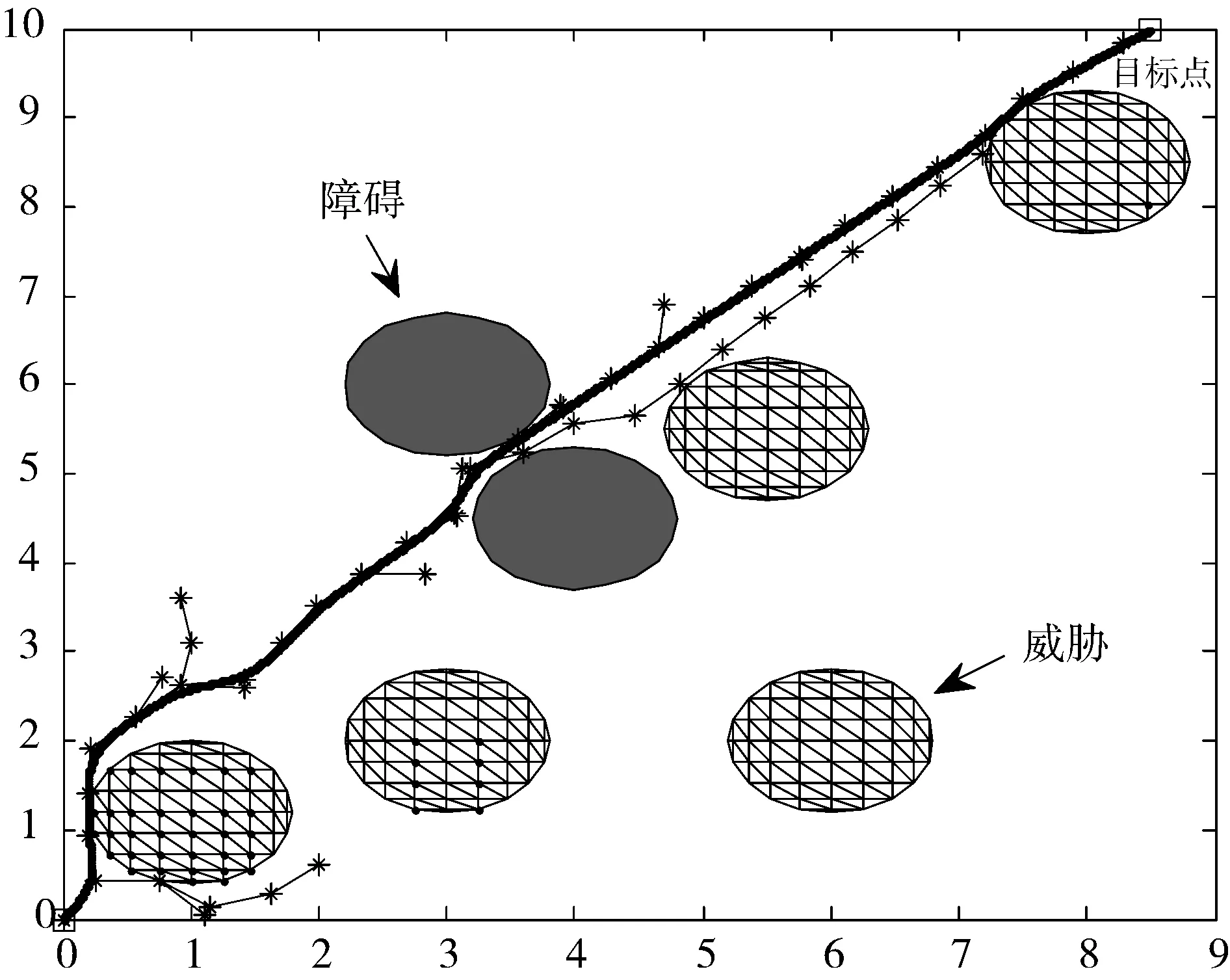

3.2 15个障碍物和威胁存在的战场态势下仿真结果




4 结束语
