一种基于改进堆优化Dijkstra算法的最小费用最大流算法
2020-04-02邓国强韩颖铮
邓国强,韩颖铮
(华南理工大学信息网络工程研究中心,广东 广州 510641)
0 引 言
在边容量、边费用有限的流网络中寻找从一个节点到另一个节点容量最大费用最小的流,称为最小费用最大流问题,是经济学和管理学的一个典型问题。现实中的物流运输、应急人流疏散、供水调度、金融现金流等都可以转化为最小费用最大流问题[1-5]。以上是最小费用最大流问题的传统应用领域,且对解决问题的时间效率要求不高。随着数据集中化、网络控制智能化,最小费用最大流问题在数据中心流量工程、计算资源调度中得到越来越多的运用,这些新兴应用领域,要求算法有较高的时间效率[6-10]。文献[6]运用最小费用最大流算法解决服务器并行作业中大规模资源调度问题。
最小费用最大流问题是在最大流问题基础之上加入最小费用限制。自1951年Dantzing[11]首次提出最大流问题形式化表达至今,大部分有效的解决办法都是以增广路径方法为基础的[12-15]。将最短路径算法应用于增广路径搜索,是解决最小费用最大流问题的最常见方法[16-19]。
增广路径方法产生的残存网络存在负权边,不能直接应用Dijkstra算法[20]搜索最短增广路径,因此如果要将该算法应用于残存网络,必需进行算法改进。文献[18-19]认为最小费用流产生的剩余网络不存在负循环[21],并通过标号法使Dijkstra算法适用于路径搜索,但2篇文献都没有给出残存网络不存在负循环的证明,并且要对所有节点进行标号,算法总复杂度为O(nm2)。
本文给出了残存网络中不存在负循环的一种证明,并改进了堆优化Dijkstra算法,在搜索最短路径过程中如果已确定最小费用的节点发现存在更小的费用则更新该节点的最小费用。这种方法具有更高的时间效率,算法更加简洁。
1 基本概念
1.1 最小费用最大流的数学模型
给定流网络G=(V,E,c,w),由节点u指向节点v的边表示为(u,v)(u,v∈V,且u≠v);边(u,v)∈E是有向的,v称为u的邻居节点,容量值0
由点s到点t的流f,经过节点u和v,要求:
对所有中间节点u∈V-{s,t},要求:
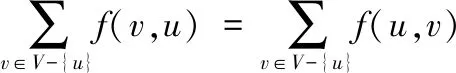
一个流f的值|f|定义为:
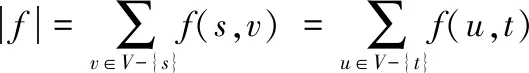
流f的费用Cost定义为:
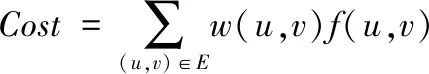
最小费用最大流算法目标就是计算出|f|值最大和Cost值最小的流f:
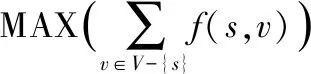
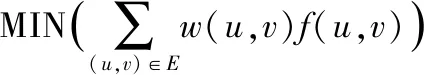
1.2 残存网络
给定流网络G和流f,残存网络Gf由G中剩余容量不为0的边和流f(u,v)产生的反向边(v,u)组成。剩余容量不为0的边的容量和费用为:
cf(u,v)=c(u,v)-f(u,v)
wf(u,v)=w(u,v)
由f产生的反向边的容量和费用为:
cf(v,u)=f(u,v)
wf(v,u)=-w(u,v)
那么,残存网络Gf=(V,Ef,cf,wf),其中:
Ef=((u,v)∈V×V|cf(u,v)>0)
1.3 节点的最小费用
源点s的最小费用为0。其他节点v(v∈V-{s})费用是从源点s出发沿有向边到达节点v的路径上所有边的费用之和。费用之和最小的路径称为最小费用路径,这个最小费用之和称为节点v的最小费用。
1.4 负权边
原始流网络G所有边的费用都是正值,但在残存网络Gf中,由f产生的反向边的容量是正值,但边费用为负值,这些反向边称为负权边。
2 算法描述
2.1 算法步骤
基于改进堆优化Dijkstra算法的最小费用最大流算法步骤如下:
步骤1以原始网络初始化残存网络。
步骤2在残存网络中,用堆优化Dijkstra算法计算汇点t的最小费用路径。计算网络中间节点最小费用时,由于残存网络存在负权边,已经确定了最小费用的节点可能出现更小的最小费用,则更新该节点的最小费用并检查是否要更新其邻居节点的最小费用。
步骤3如果残存网络中找不到汇点t的最小费用路径则算法结束,返回最小费用最大流。如果残存网络中找到汇点t的最小费用路径,根据该路径的最小带宽,进行反向增广,更新残存网络,重复步骤2。
2.2 算法分析
堆优化Dijkstra算法即在Dijkstra算法过程中运用最小堆实现最小优先队列。算法步骤2采用堆优化Dijkstra算法搜索残存网络中源点s到汇点t的最小费用增广路径,从源点s出发直到堆弹出汇点t的最小费用停止计算,得到当前网络中t的最小费用增广路径。由于残存网络存在负权边,已经确定了最小费用的节点可能出现更小的最小费用,则更新该节点的最小费用并检查是否要更新其邻居节点的最小费用。如果存在负循环,步骤2将出现无限次循环更新节点最小费用的情况。下面证明在原始网络边费用为正、容量有限前提下,以上方法产生的残存网络不存在负循环。
流网络中节点数为n,边数量为m。如果采用二叉堆,且只运用压入和弹出操作,则堆中节点数上限为m,改进堆优化Dijkstra算法复杂度为O((n+m)lgm);如果二叉堆中运用压入、弹出、减小值操作,则堆中节点数上限为n,改进堆优化Dijkstra算法复杂度为O((n+m)lgn);如果采用斐波那契堆[17],运用压入、弹出、减小值操作,改进堆优化Dijkstra算法复杂度为O(nlgn+m)[20]。
2.3 证明
定理1 在边的费用为正、容量有限的流网络中,采用最短路径算法搜索最小费用最大流增广路径,循环搜索过程中产生的残存网络不存在负循环。
证明如图1所示,节点a、b、c以及3条有向实线,是残存网络中的节点和边。负权边(a,b)是在之前某个残存网络上最小费用流fP增广产生的反向边,其对应的正向边(b,a)是节点b到节点a的最小费用边。即在之前某个环节的残存网络中,w(b,a)w(b,c)+w(c,a),那么0w(b,c)+w(c,a)-w(b,a)。即在当前残存网络中心,节点a、b、c构成的圈不是负循环。存在更多节点的圈,都可以简化为这样的三点圈,并遵守相同的规律。
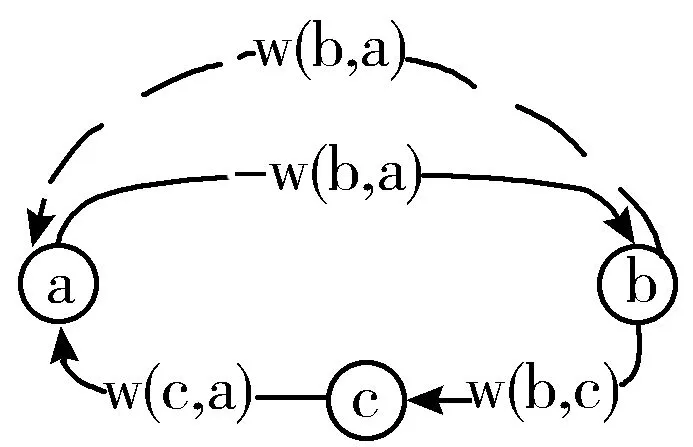
图1 存在负权边的圈
3 实 验
3.1 实验环境和数据集
实验平台采用Intel Core i5-6200U CPU @2.30 GHz 2.40 GHz处理器、8.00 GB内存,用Python语言编写。
为了验证本文算法,通过生成随机流网络,分别在节点规模、边稠密度上比较本文基于改进堆优化Dijkstra算法的最小费用最大流算法与基于最短路径快速算法(Shortest Path Faster Algorithm, SPFA)算法[22-23]的最小费用最大流算法、基于Bellman-Ford算法的最小费用最大流算法比较平均时间消耗。SPFA算法和Bellman-Ford算法都是在存在负权边网络中求解最短路径问题的经典算法。
常见的最小堆有二项堆和二叉堆。斐波那契堆虽然算法复杂度看起来比前2种堆更优,但带有非常大的常数,实现代码复杂,适用于节点达到一定数量级的网络。本文算法的改进堆优化Dijkstra选用了二叉堆。
网络节点数量为n,节点连接概率为e,采用以下方法生成流网络数据集:
1)中间节点标号为2~n-1,节点i存在边指向节点j的概率为e;不存在指向节点自身的边;如果存在边从节点i到节点j,则不存在反向的边。
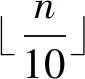
3)边的容量为小于n的随机正整数。
针对每个(e,n)组合,随机生成50个网络图,用算法分别计算50个流网络的最小费用最大流,得到平均时间消耗。
3.2 计算结果及性能的比较
3种算法都可以用比较简洁的代码实现。计算过程中,3种算法计算出的最小费用最大流结果均一致。图2描绘了不同(e,n)组合下,3种算法的平均时间消耗的曲线。表1列举了不同组合下,不同算法平均时间消耗的比值,其中:
比值1=
比值2=
实验结果验证了本文提出的基于改进堆优化Dijkstra算法的最小费用最大流算法适用于边的容量和费用都是正值的有向流网络,时间消耗是基于SPFA的算法的3/10左右,是基于Bellman-Ford的算法的2/25左右。
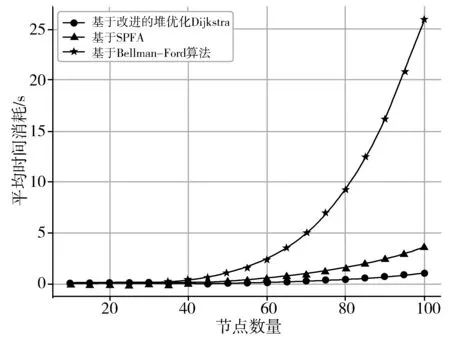
(a) 基于节点规模的平均时间消耗曲线(节点连接概率为0.5)
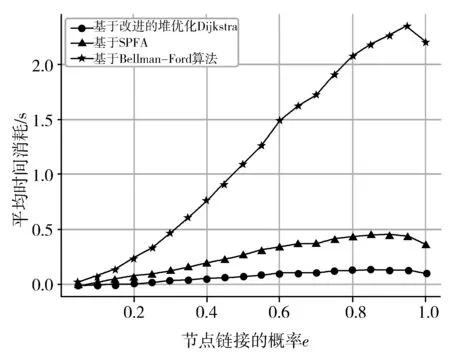
(b) 基于边稠密度的平均时间消耗曲线(节点数量为50)
表1 平均时间消耗比值
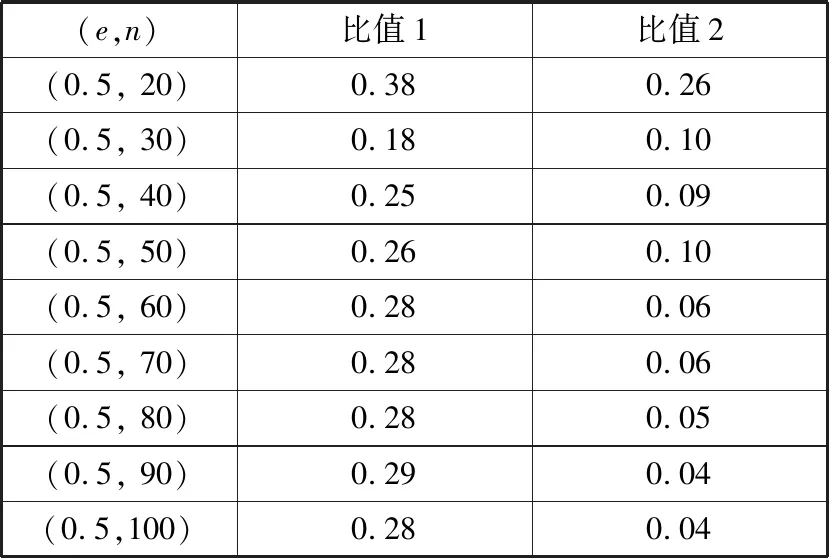
(a)基于节点规模的平均时间消耗比值(节点连接概率为0.5)
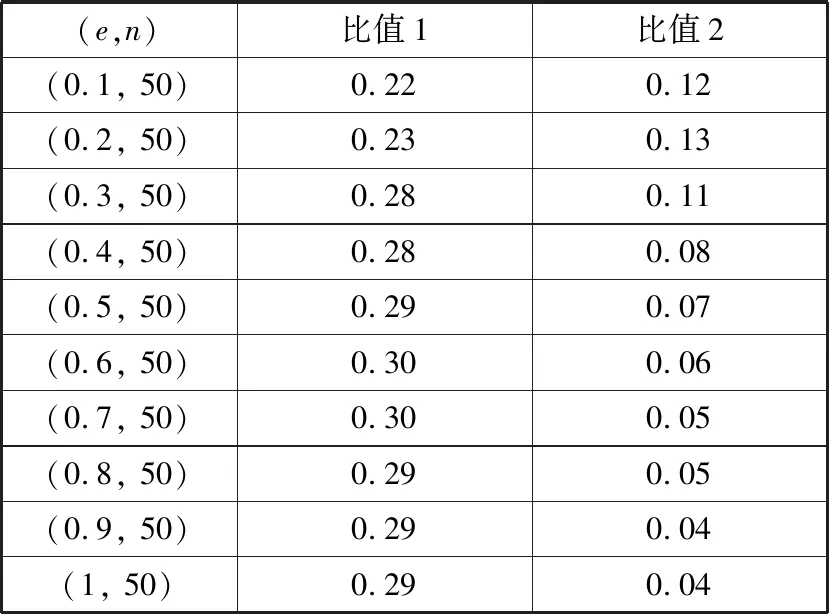
(b)基于边稠密度的平均时间消耗比值(节点数量为50)
4 结束语
最短增广路径搜索是最小费用最大流算法的核心。本文证明了在边费用为正的流网络运用最短路径算法搜索最小费用增广路径,产生的残存网络不存在负循环;改进了堆优化Dijkstra算法,使其适用于存在负权边的残存网络。通过实验,验证了本文算法计算结果是正确的。本文算法实现代码简洁,与基于SPFA算法、Bellman-Ford算法的最小费用最大流算法相比较,在时间消耗方面表现更优秀。
