大型海上风电场风机排布优化策略研究

李 岩，吴 迪，洪 畅，刘怀西，葛文澎

(明阳智慧能源集团股份公司，中山 528437)

0 引言

随着化石能源面临愈发严峻的匮乏局面，可再生能源在世界范围内得到了重点关注。作为可再生能源之一的风能，以储量巨大、分布广等优势，得到了大力地开发利用，尤其是海上风电，已成为风电行业发展的主方向[1]。在海上风电场逐步走向大型化、商业化的同时，如何提升风电场整体效益，降低建造、运营成本已成为行业内重点关注的议题。

目前，部分学者对如何合理布置海上风电场风机机位进行了相关研究。GONZALEZ等[2]提出的栅格形式的风机布置能有效提高风电场收益；DUPONT等[3]提出了一种多级拓展图形搜索算法，该算法能同时对风机机位和风机尺度进行优化；GAO等[4]应用多种群遗传算法结合二维Jensen-Gaussian尾流模型对海上风电场进行了优化研究，结果显示该模型能较精确地预测风机尾流特性并得到较优的机位排布方案；WU等[5]同样应用遗传算法对风机机位优化进行了研究分析，并结合蚁群算法对风电场集电线路规划进行了探究，但该类智能算法通常适用于边界较规则的风电场，若风电场边界形式复杂则优化过程较难实现。本文以海上风电场为研究对象，提出了一种适用于任意几何边界形式的风电场风机机位优化策略，该策略能有效降低整个风电场尾流损失，提升风电场发电量，可为实际风机排布提供理论和工程实践参考。

1 风电场模型

1.1 风资源评估

评估某地区风资源情况，通常需要获取该地区不短于1年的实际测风数据。由于时序风速数据样本数较大，统计工作繁杂，因此风速数据常使用威布尔分布函数进行描述，该函数可以计算出任一来流风速u下的风频比例p(u)，具有较好的直观性。

威布尔分布函数为：

式中，C为威布尔分布尺度参数，m/s；K为威布尔尔分形状参数；u为来流风速，m/s。

进行风资源评估时，通常将风向分为多个均匀分布的扇区，并分别拟合出各风向扇区下的风速威布尔分布函数，从而得到不同风向扇区下的C值、K值。

1.2 尾流模型

当来风沿某一风向经过风电场时，上游风机在获取风能的同时会在下游产生风速下降的尾流亏损区，使得下游风机因来流风速减小而导致发电量降低，这种现象称为尾流效应。尾流效应受风资源情况、风电场风机排布、风机参数等多方面因素的综合影响。

目前行业上，Jensen尾流模型是应用最广泛的一种尾流模型，该模型在1986年由JENSEN等提出，其假设风机后部的轴对称尾流区亏损是呈线性恢复的[6]。Jensen尾流模型示意图如图1所示。图中，Aoverlap为下游风机盘面与上游风机尾流截面的重叠面积，m2；Awt2为下游风机扫风面积，m2；Awakeloss为上游风机尾流截面面积，m2；uloss为来风由于上游风机的尾流导致的风速降低值；wt1为1#风机；wt2为2#风机。

该模型用尾流衰减因子k来表征尾流区的扩张程度，当下游风机位于上游风机尾流区时，下游风机处的风速降低因子Cwake的计算式为：

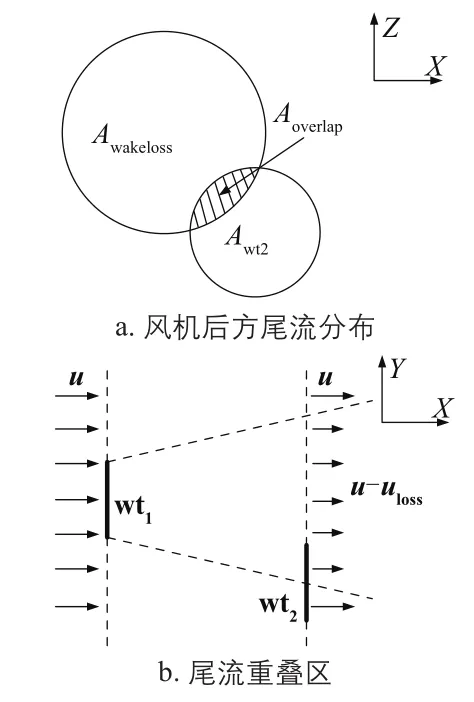
图1 Jensen尾流模型示意图Fig.1 Diagram of Jensen wake model

式中，Ct为风机推力系数，其值取决于风机来流风速；D为风机直径，m；x为平行于风向的距离。

尾流衰减因子k可按经验公式(3)计算[7]，即：

式中，h为风机轮毂高度，m；z0为地表粗糙度高度，m。

当1台风机受多台风机尾流联合影响时，尾流亏损的累计效应常采用平方和开根号的方法进行计算[8]。对于海上风电场而言，海面的粗糙度高度为0.0002 m[9]，按式(3)计算，当轮毂高度为100 m时，k值约为0.0381。

1.3 发电量计算

风电场实际年发电量PAEP的计算需要风机的功率、推力曲线、风机位置和风资源等信息，其计算式为：

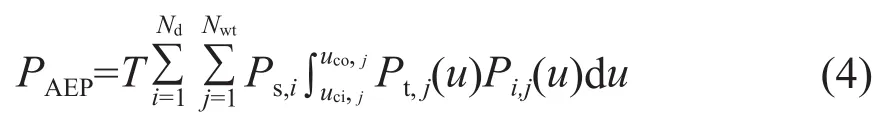
式中，T为一年中的小时数，h，取8760 h；Nd为均匀划分的风向扇区总数；Nwt为风电场中实际风机数量；Ps,i为第i风向扇区下的风频；uci,j为第j台风机的切入风速，m/s；uco,j为第j台风机的切出风速，m/s；Pt,j(u)为第j台风机在来流风速u下的输出功率，MW；Pi,j(u) 为第j台风机在第i风向扇区下的风频。

目前常用的风资源数据统计方法是将测风数据转化为风速风向联合分布矩阵，在每一风向及风速子区间内进行发电量计算，然后按加权方式求和，即可计算出风机发电量。风电场的利用效率常用容量因数η表征，该参数为风电场风机全年实际发电量与全部风机全年持续满功率发电量之比，其计算式为：

式中，Pe,j为第j台风机的额定功率，MW。

风机尾流损失值δwake为风机由于尾流亏损造成的年发电量损失与理论年发电量之比，其计算式为：

式中，Ptheory为风电场理论年发电量，MWh，其是根据风机功率曲线和轮毂高度处的风速频率分布估算得到的全场风机的年发电量，未考虑风电场尾流效应的影响。

2 尾流模型的准确性验证

本文算例中风电场尾流模型选用Jensen尾流模型，利用Python语言对该模型进行程序实现，输入风机机位点位置、风机参数、风资源等信息，便可快速求解出各个风机机位点的发电量及尾流损失值。

为验证Jensen尾流模型的准确性，以Horns Rev 1海上风电场作为研究对象。Horns Rev 1海上风电场位于丹麦东北海域，离岸距离约15 km，由80台维斯塔斯公司V-80-2MW型风机组成，风机的轮毂高度为70 m，风机直径为80 m。该风电场风机的机位布置图如图2所示[10]，图中，Dw为风向角度。

图2 Horns Rev 1海上风电场的风机布置图Fig.2 Layout of wind turbines in Horns Rev 1 offshore wind farm

对比来流风速区间在8±0.5 m/s范围、风向区间分别在 270°±5°和 222°±5°范围时，风电场部分风机的尾流损失情况，其中，各风机尾流损失的实际值来源于文献[11]中记录的风电场实际监测数据。图3为基于Jensen尾流模型的Horns Rev 1海上风电场部分风机机位点尾流损失预测值与实际值对比图。

图3 不同风向时，Horns Rev 1海上风电场风机机位点尾流损失预测值与实际值对比Fig.3 Comparison of predicted and actual values of wind turbines' wake loss in Horns Rev 1 offshore wind farm, under different wind directions

从图3可以看出，Jensen尾流模型的风机尾流损失预测值与实际值吻合度较高，同时预测值整体高于实际值。当风向区间为270°±5°时，尾流损失预测值比实际值平均高12.1%；当风向区间为222°±5°时，尾流损失预测值比实际值平均高6.7%。经分析，这一差异主要是源于Jensen尾流模型是假设风电场中各风机机位点处的风向、风速均一致，而实际风电场无法满足该假设，因此不可避免会引入一定误差。从风电场风机机位尾流损失的快速预测方面考虑，Jensen尾流模型预测值与实际值的误差在可接受范围内，即Jensen尾流模型在风电场风机尾流损失预测中具有一定的适用性与准确性。

3 风机机位优化流程

3.1 规则型排布优化

在规则型风机机位排布中，风机呈栅格形式布置，布置的最小单元为平行四边形，如图4所示。这类布置形式的风电场风机排布由以下参数定义：风电场内风机排数N1与列数N2，列间距d1，排间距d2，每一排风机与水平轴的夹角α(水平轴指向正东方向)，风机排与列的夹角β。

图4 规则型风机排布方案示意图Fig.4 Diagram of regular wind turbine layout scheme

在风机排布方案制定前，需明确风电场的场址范围(如图4中红色四边形示意风电场边界)和风机布置的预安装台数Npreinstall。在风机的规则型排布优化过程中，对d1、d2、α和β等参数进行遍历取值，以全场最大发电量为优化目标。本文借助Python语言实现了该优化过程，风机尾流模型仍选用Jensen模型，通过高性能计算机，能在可接受的时间内完成风机的规则型排布优化过程。

优化过程中，风机机位应满足以下限制条件：各风机之间距离均不小于极限安全机距dmin；风电场边界内风机实际安装数量Nwt与预安装台数Npreinstall一致。即：

式中，第a台风机的地理坐标为(Xa,Ya)；第b台风机的地理坐标为(Xb,Yb)。

在优化过程中，参数d1和d2的取值下限为dmin，取值上限由风电场的面积决定；参数α的取值范围为[0°,180°)；参数β的取值范围一般为 [15°,165°]，这是由于当β接近 0°或 180°时，会使风电场内风机的列和排布置大致趋于一条直线，这与实际经验不符。

3.2 随机型迭代优化

风电场风机机位的随机型迭代优化过程是在规则型排布优化之后，以最优的规则型排布方案作为随机型迭代优化的初始方案，对风电场风机机位点进行随机位置调整，机位点的尾流损失值越大，则进行位置调整的几率越高；调整过程中应保持所有风机位置均不超出风电场边界范围，同时限制风机的最小机距不小于极限安全机距dmin。每次机位方案更新后进行发电量计算，若新方案的发电量高于前一方案，则替换掉前一方案。按此流程不断进行风机机位的迭代优化，直至最新机位排布方案的发电量无法进一步提升，即找出了发电性能最优的风机排布方案。

通过已有算例验证，该优化方法获得的风机机位方案的发电量明显高于规则型排布方案，发电量提升幅度通常与风电场区面积、形状及风机台数等因素有关。

4 优化算例

以Horns Rev 2海上风电场作为研究对象对优化方案进行计算。Horns Rev 2海上风电场位于丹麦东北海域，离岸距离约30 km，由91台西门子SWT2.3-93型风机组成，总装机容量为209.3 MW，风电场占海面积约为33 km2[12]。

以距该风电场中心100 m处Merra 2中尺度风资源数据作为测风数据，各风向扇区下的风频Ps及风速威布尔分布参数如表1所示。考虑到海上风机逐渐走向大型化的趋势，在此以明阳智慧能源集团股份公司的MySE3.0-121型海上风机作为推荐机型。该机型额定功率Pe为3.0 MW，风机直径D为121 m，轮毂高度h选取100 m，切入和切出风速分别为3.0 m/s和25 m/s；结合Horns Rev 2海上风电场的总装机容量，推荐风机总数为70台。

表1 Horns Rev 2海上风电场的风资源参数Table 1 Wind resource parameters of Horns Rev 2 offshore wind farm

4.1 规则型排布方案优化算例

在方案优化过程中，为研究风机间最小距离对风电场发电量的影响，对上述风电场进行优化排布时限制风机间最小距离分别不小于3.0D、4.0D和5.0D，即dmin分别取3.0D、4.0D和5.0D。通过优化得出的最优方案布置图如图5所示，不同极限安全机距时最优方案的发电量信息如表2所示。

图5 最优规则型排布方案的风机布置图Fig.5 Arrangement diagram of optimal regular wind turbine layout scheme

表2 各规则型排布方案参数及发电量Table 2 Parameters and energy productions of each regular layouts

由表2数据可知，风机极限安全机距dmin为3.0D的方案的发电量最优，然后依次为4.0D方案和5.0D方案。该结果说明，在一定范围内极限安全机距越小，得到的规则型排布方案的发电量越高。但由于过小的风机间距不利于风机的安装及运维，因此行业上常建议最小风机间距不小于3.0D。此外，3组排布方案中α的取值均为88°左右，同时该风电场内主风向为正西方向，即最优规则型排布方案中各排风机的连线均大致与主风向垂直。

4.2 随机型迭代优化方案算例

风电场风机机位随机型迭代优化过程中，在调整尾流损失较大的风机的位置时，同样需限制风机间最小距离。在此以上述3组规则型排布方案作为初始方案，分别进行随机迭代优化，优化过程中依然分别限制风机间最小距离不小于3.0D、4.0D和5.0D。优化后最终方案布置图如图6所示，3组随机型排布方案的参数及发电量如表3所示。

图6 最优随机型排布方案的风机布置图Fig.6 Arrangement diagram of optimal random wind turbine layout scheme

由表3数据可以得出，通过随机型迭代优化过程可进一步提升整个风电场发电量，本算例随机型排布方案的年发电量在规则型排布的基础上平均提升了约1.35%，且优化时间可接受。通过对比这3组排布方案发现，在一定范围内，极限安全机距越小，风电场发电量越高。

表3 各最优随机型排布方案的参数及发电量Table 3 Parameters and power generation of each optimal random layout

4.3 小结

综上所述，就发电量而言，随机型排布优于规则型排布，但随机型排布中风机布置通常没有规律性，缺乏美观且电缆布置较复杂，因此在实际工程项目中，还需慎重对比选择2种机位优化策略。

5 结论

本文以Horns Rev 1海上风电场为例验证了Jensen尾流模型的准确性，数据显示基于该尾流模型计算得出的不同风向下风机输出功率与实际值较吻合，表明Jensen尾流模型能较准确地预测大型海上风电场中风机间尾流影响程度。通过Python语言程序实现大型海上风电场规则型排布方案的自动优化，在可接受时间内得到了发电量最优的风机规则型排布方案，且最优规则型排布方案中各排风机的连线均大致与主风向垂直。机位随机型迭代优化策略在规则型排布优化之后，通过随机调整尾流损失较高的风机位置，可达到进一步减小整个风电场尾流损失的目的。文中的Horns Rev 2海上风电场算例显示，随机型排布方案的年发电量可在规则型排布方案的基础上平均提升约1.35%。