基于模糊BP 神经网络的高原寒区弹药换算系数研究*

史宪铭，赵汝东*，骆兴远，张建军，宋 星

（1.陆军工程大学石家庄校区装备指挥与管理系，石家庄 050003；2.新疆军区，乌鲁木齐 830001；3.解放军32140 部队，石家庄 050061）

0 引言

弹药作为一种特殊的战备物资，其供应保障是战争致胜的关键制约因素。弹药换算系数是指非标准条件下的弹药消耗量与标准条件下的弹药消耗量的比值。在战役级弹药消耗预计中，以标准情况下的弹药消耗量为基准，通过乘以换算系数的方式，可以方便地确定特定情况下的所需弹药数量。可见，换算系数的精确与否直接关系着弹药消耗量预测的准确程度，如何准确确定弹药换算系数，是当前研究弹药消耗量的一个重点和难点问题。

应用神经网络对弹药消耗量预计，是当前弹药需求预计的一种有效方法。孙云聪、万华［1］分别采用基于Elman 和BP 网络方式，以载机生存概率、毁伤程度、打击精确度、破甲能力为重点影响因素，对航空训练弹药需求预测进行了对比研究；刘涛、彭世蕤［2］着重从载机突防能力、目标类型、打击精确度、对目标破坏程度的影响出发，运用基于改进BP神经网络对航空弹药预测问题进行了研究；齐浩淳等［3］运用BP 神经网络对高寒山地平时弹药消耗量进行了研究；俞杰等［4］对反装甲单目标弹药预计问题进行了分析。上述研究中，缺乏专门针对高原寒区弹药消耗量进行专门分析，并且在考虑影响因素方面，对于难以定量的因素考虑不全，缺乏考虑定性到定量的转换方法。

基于此，本文以高原寒区的弹药预计为研究背景，通过对高原寒区弹药消耗影响因素进行针对性分析，增强高原寒区弹药消耗预计的适应性。运用隶属度函数将定性指标转化为定量指标，解决了非线性系统BP 模型解析困难的问题。通过作战实例验证此方法的便利性和精确性。

1 弹药换算系数测算模型构建

BP 神经网络是误差反向传播神经网络，是一种有导师的误差反向后传型多层前馈网络，是目前研究最多的网络形式之一，适用于多输入单输出问题的优化解决。本文利用输入为模糊隶属度的BP 神经网络解决多因素影响下的弹药换算系数优化问题。

1.1 BP 神经网络架构

BP 神经网络为分层型网络，通常由输入层、隐含层和输出层3 层构成，各层之间通过连接权进行连接。根据Kolrnogorov 定理，3 层BP 神经网络能够实现对任意非线性函数的逼近［5-7］，本文模型选取只有一个隐含层的3 层BP 神经网络模型。隐含层在学习过程中起着特征探测与提取的作用，隐含层单元数的选取关系到学习的收敛性、容错性及精度，因此，存在一个最佳的隐单元数，可参考公式［8］：

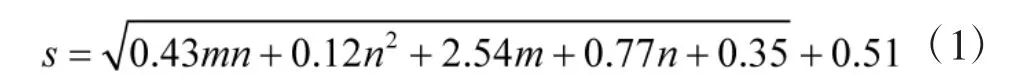
BP 神经网络的学习由模式顺传播和误差逆传播组成。信号进入输入层，经过各层连接权、阈值、响应函数的传递输出到输出层；输出层输出学习结果并与期望输出值进行比较，将误差信号反向传递，不断调整各层连接权和神经元阈值来减小误差。通过上述过程反复迭代获取相对理想的连接权和阈值。

1.2 输入量的选取

用BP 神经网络对弹药消耗量换算系数进行优化，把作战类型与样式、作战持续时间、部队综合战斗力指数、气象地理条件、对抗激烈程度等影响因素作为输入量。激活函数选择具有平滑和渐进性的Sigmoid 函数［9］，输出值的取值范围为［0，1］，借助隶属度函数求得的模糊隶属度恰好符合此要求，所以把各影响因素的隶属度作为BP 神经网络的输入值。

1.3 网络结构确定

本文采用的3 层网络结构输入层单元个数为5个，输出层单元只有1 个，即弹药消耗量换算系数。通过式（1）求得隐含层的单元数取5 个最恰当，隐含层的神经元激活函数为tansig 函数。高原寒区弹药换算系数优化的BP 神经网络模型如图1 所示。

图1 高原寒区弹药换算系数优化的BP 神经网络模型

2 高原寒区弹药消耗主要影响因素确定

2.1 影响因素分析

结合高原寒区作战实际，主要从作战类型与样式、作战持续时间、部队综合战斗力指数、气象地理条件、对抗激烈程度等5 个方面进行分析［10］，为下一步指标量化及BP 神经网络构建打好基础。

2.1.1 作战类型与样式

作战样式主要有阵地防御进攻战斗、对立足未稳之敌的进攻战斗、对机动防御之敌的进攻战斗以及阵地防御战斗、运动防御战斗、机动防御战斗等［9］。由于地形地势的原因高原寒区作战样式多为通道防御反击作战，防御战斗的弹药消耗量较进攻战斗会大幅降低。

2.1.2 作战持续时间

研究组行MRI诊断，操作如下：采用Philips 1.5T的MRI设备，患者受检之前需禁止饮食、饮水，扫描层厚参数为8mm，扫描间隔参数为1mm，检查时，静脉注射15ml对比剂。操作者需密切留意患者癌变性质，并对影像特征进行分析。

高原寒区自然环境恶劣、山高谷深、机动道路少、交通条件落后，战时保障极为困难，战斗需要尽量速战速决，这种情况下多以压制性武器火力覆盖，在短时间内消耗大量弹药；再者山谷地带隐蔽条件差，部队长时间停留容易遭遇敌方侦察与火力打击，快速机动通过是有效解决此问题的手段，此情形下不易产生正面交锋，因此，弹药消耗相对较少。现代高技术条件下作战，各种作战力量的机动性大幅提高，强调出奇制胜快速打击敌方要害，缩短作战持续时间，该情况下使用精确制导弹药速战速决降低了普通弹药消耗数量。

2.1.3 部队综合战斗力指数

部队综合战斗力指数主要受到首长指挥水平、士兵作战能力、装备性能发挥等因素的影响。首长和士兵是战斗的主体，影响着作战进程和战斗力的生成。首长指挥水平受到指挥经验的影响，而士兵作战能力受到高原寒区作战环境恶劣的制约，士兵生理功能和心理状态受到影响更大。武器装备是作战的载体，装备性能发挥受到通联水平、机动性能、打击能力及其防护能力等战技术性能影响。高原寒区作战易导致机械动作失灵，操作困难，人装结合度较低，并且空间狭小不利于武器装备的展开部署和机动配置，影响武器装备作战效能的发挥，对于弹药消耗影响较大。

2.1.4 气象地理条件

高原寒区气象条件恶劣，地理环境复杂，弹药消耗量较普通地区差异较大，在考虑弹药消耗影响因素时气象地理条件所占权重较高，主要包括地形和气候两个方面。高原通道窄、纵深长，地形复杂多变，道路崎岖，植被稀少，对部队的机动与隐蔽影响极大，弹药的非战争损失量增大。在气候方面，高原寒区海拔较高、空气稀薄，空气阻力相对较小，风力较大，弹药散布程度有一定的增大，容易导致弹道偏移，影响其射击精度，造成弹药消耗增多。

2.1.5 对抗激烈程度

对抗激烈程度主要包括参战兵力和作战强度两方面。在参战兵力上，高原寒区作战样式多为通道作战，作战区域狭长，一次性投入的兵力与平原开阔地带相比较少。在作战强度上，作战强度较大时，作战双方为了完成作战任务，会在较短时间内投入较多的作战力量。作战强度越大，单件武器在单位时间内的使用强度越大，弹药消耗就越多。

综上所述，高原寒区作战弹药消耗主要影响包括作战类型与样式、作战持续时间、部队综合战斗力指数、气象地理条件、对抗激烈程度等5 个主要方面，影响因素结构如图2 所示。

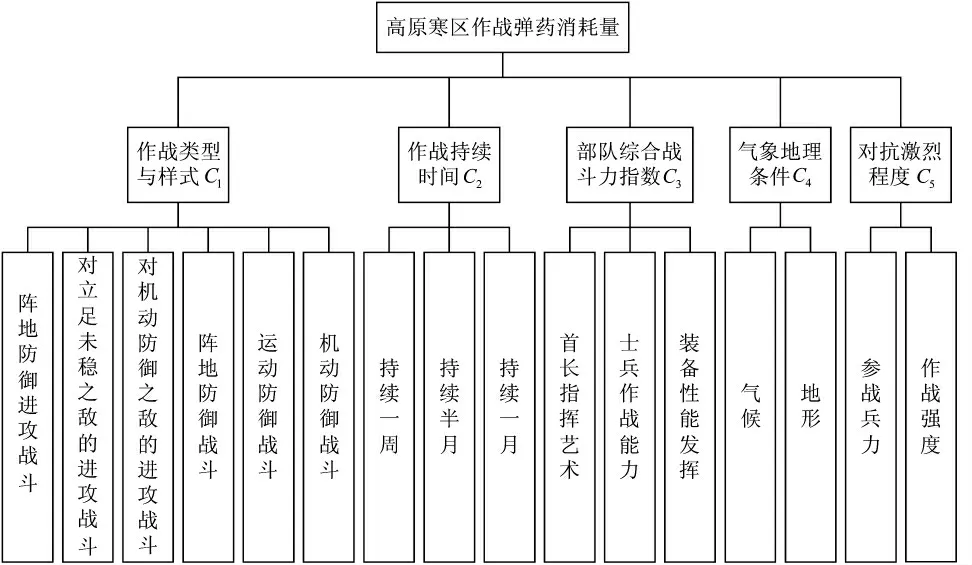
图2 弹药消耗量主要影响因素

2.2 基于模糊隶属度的弹药消耗影响因素量化处理

对弹药消耗量影响因素的量化处理采用模糊方法，根据各影响因素的相关性，求取其隶属度函数。在解决模糊问题过程中确定隶属度函数是关键性一步，隶属度函数的选用须结合各因素影响情况寻求最恰当的表达式。隶属度函数的取值介于0 和1 之间，用以表示影响因素对弹药消耗的影响程度。本文根据以往作战数据和指挥经验，由专家对作战类型与样式、作战持续时间等5 个因素打分赋值，按照隶属度函数确定的方法与原则建立各影响因素的隶属度函数，进行量化［12］。

2.2.1 作战类型与样式隶属度函数C1

邀请不同专家对高原寒区作战类型与样式进行评判，结合作战样式运用的可能性及其弹药消耗情况，对阵地防御进攻战斗、对立足未稳之敌的进攻战斗、对机动防御之敌的进攻战斗以及阵地防御战斗、运动防御战斗、机动防御战斗进行模糊综合评判，确定其隶属度函数。

2.2.2 作战持续时间隶属度函数C2

弹药消耗量与作战持续时间成正相关，作战持续时间越长，弹药消耗量越大。可以得出作战持续时间与其隶属度函数近似满足“升半Γ 型分布”［13］，如图3 所示。

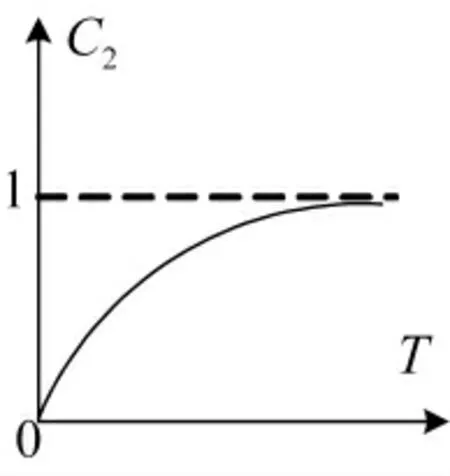
图3 作战持续时间隶属度函数

作战持续时间隶属度函数为：

其中，T 表示持续时间，m 表示与时间有关的系数。

2.2.3 部队综合战斗力指数隶属度函数C3

一般情况下，首长指挥艺术越高，士兵作战能力越强，装备性能发挥越好，弹药的消耗量在一定程度上就越少，甚至达到不战而屈人之兵的效果。部队综合战斗力指数与其隶属度近似于“降半Γ 分布”［11］，如图4 所示。可以分析得出隶属度函数为：

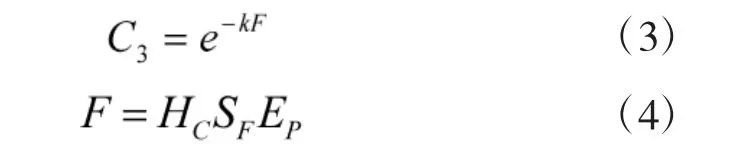
其中，k 为调节系数，F 表示部队综合战斗力指数，HC表示首长指挥艺术指数，SF表示士兵作战能力指数，EP表示装备性能发挥指数。

2.2.4 气象地理条件隶属度函数C4

图4 部队综合战斗力指数隶属度函数

高原寒区气象条件差，空气稀薄，射弹散布严重，导致弹药消耗增多；地形复杂多变，道路崎岖，造成弹药非战斗损耗增多。可见气象地理条件与弹药消耗成反比，气象地理条件与其隶属度函数近似满足图4。气象地理条件的隶属度函数为：

其中，M 表示气象因子，G 表示地理因子，n 表示与气象地理条件相关的系数。

2.2.5 对抗激烈程度隶属度函数C5

作战双方对抗激烈程度主要取决于参战兵力与作战强度，作战强度越大，投入兵力越多，弹药消耗量越大，弹药消耗量与之成正比。对抗激烈程度与其隶属度函数基本满足“升半Γ 型分布”，隶属度函数表示为：

其中，I 表示作战强度因子，N 表示参战兵力基数，l表示与对抗激烈程度相关系数。

3 应用验证

本文选取有关高原寒区作战等实例数据，借助隶属度函数公式计算出各影响因素的隶属度，模糊隶属度作为弹药换算系数测算模型的输入，输出为弹药换算系数。而后结合5 个主要的弹药消耗影响因素对BP 神经网络进行学习训练，学习样本如表1所示。

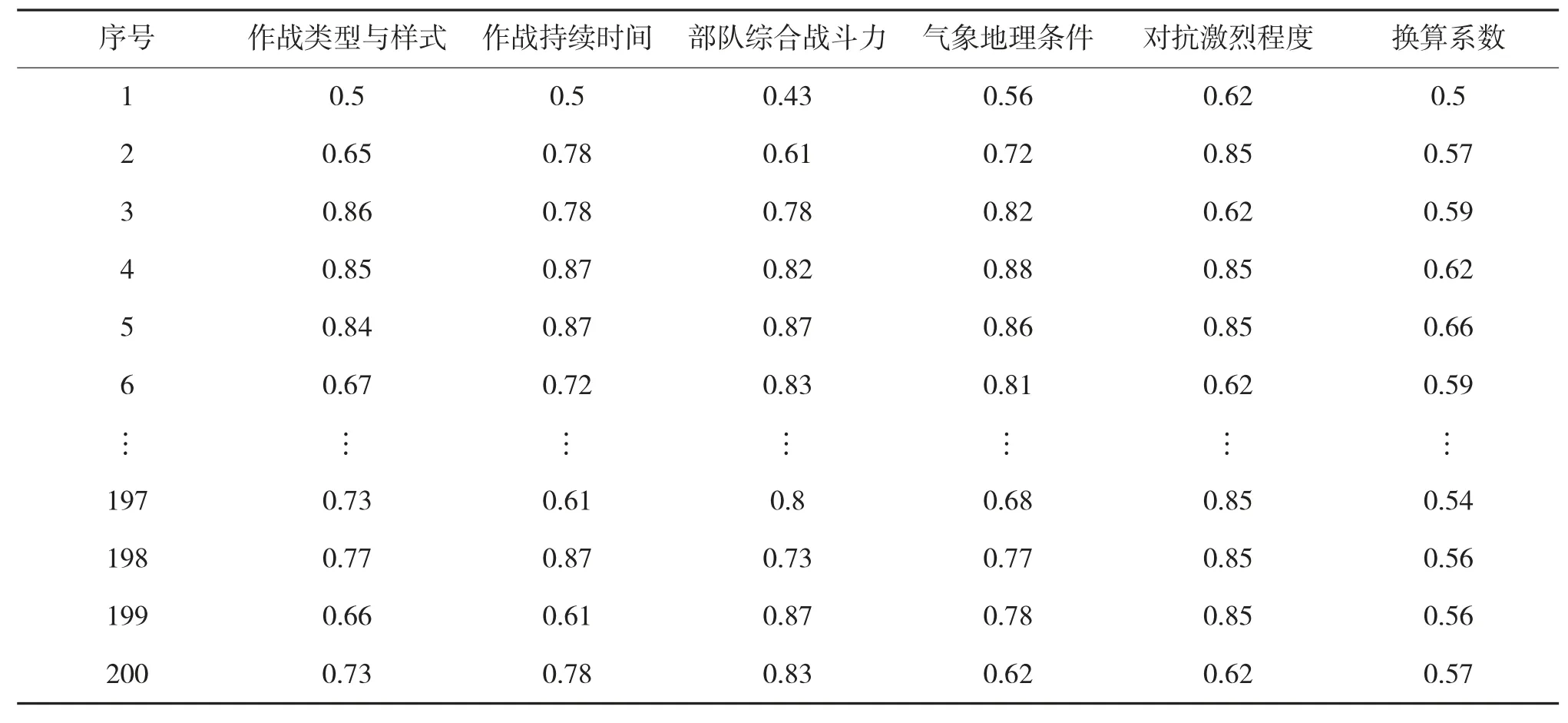
表1 BP 神经网络学习样本

运用BP 神经网络模型对弹药消耗量换算系数进行优化［14］，选取了200 组实战数据作为学习样本，设置学习速率为0.1，学习次数为40 000，目标精度为0.001。从图5 中可以看出，当训练37 066次后，达到目标精度0.001，训练停止。给定数据的仿真结果与实际数据比较接近，误差能控制在较低范围内。

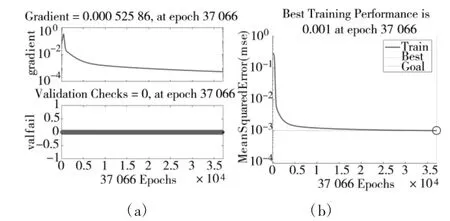
图5 弹药消耗量换算系数训练误差变化曲线

借助训练完的模糊BP 神经网络，将表2 中验证样本输入，可得到弹药消耗量换算系数测算值。

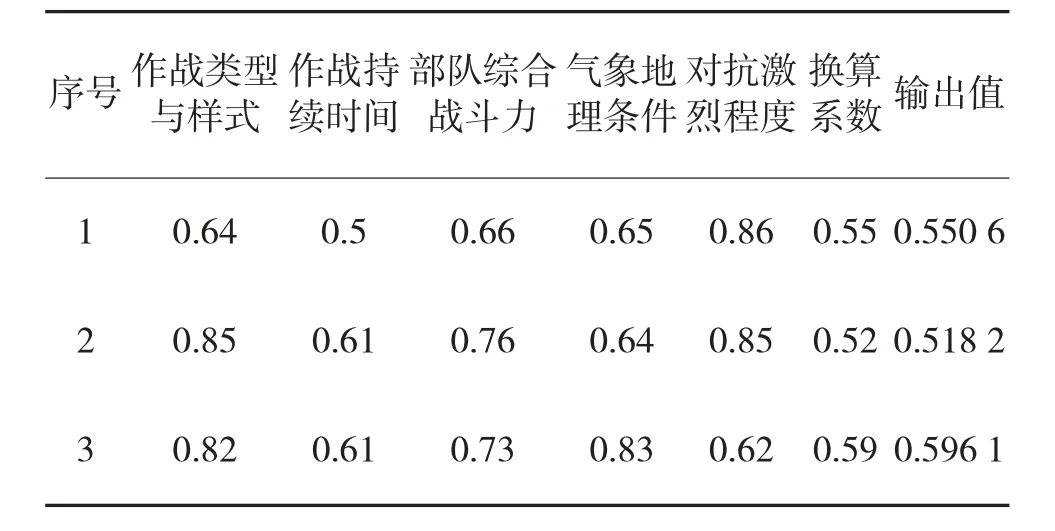
表2 BP 神经网络验证样本

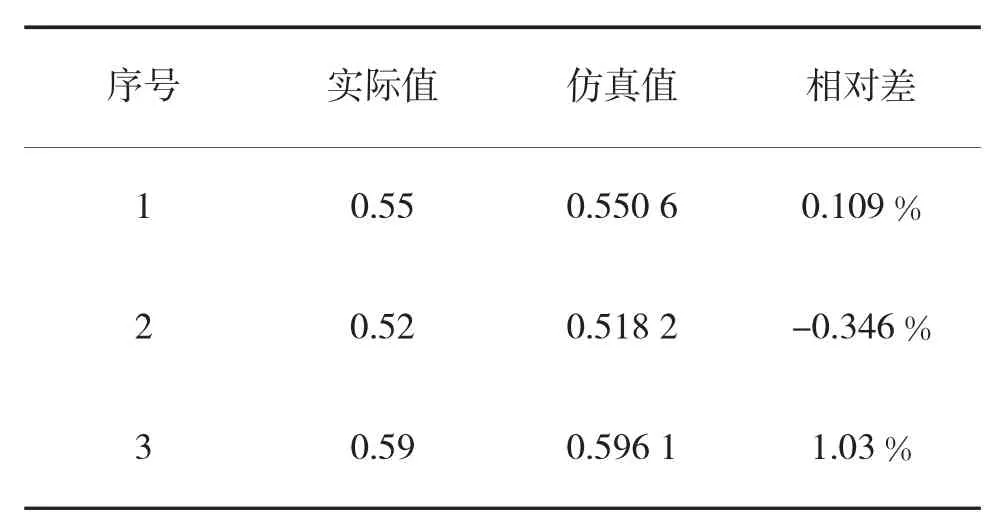
表3 换算系数实际值与仿真值对比

通过表3 可发现，利用弹药换算系数测算模型计算的弹药换算系数与实际数据一致性较好，误差能控制在合理范围之内，能够较为准确地对弹药消耗量进行预计，此模型具有可用性，可以推广至其他作战环境下的弹药换算系数测算。

4 结论

本文分析了作战类型与样式C1、作战持续时间C2、部队综合战斗力指数C3、气象地理条件C4、对抗激烈程度C5等影响高原寒区弹药消耗的主要因素，结合模糊隶属度函数对其进行量化处理并构建基于模糊BP 神经网络的弹药换算系数测算模型，将定性问题定量化，解决了非线性系统难以建立解析数学模型的问题。仿真实验借助模糊BP 神经网络有效验证了优化所得的弹药换算系数科学准确，对我军弹药保障具有很大的参考价值，极大提高了弹药精确保障能力。