考虑裂尖塑性区影响的水力压裂缝高计算模型

李玉伟，龙敏，汤继周，陈勉,3，付晓飞

（1.东北石油大学石油工程学院，黑龙江大庆 163318；2.School of Engineering and Applied Sciences, Harvard University，Cambridge 02138，USA；3.中国石油大学（北京）石油工程学院，北京 102249）

0 引言

水力压裂作为一种高效的增产工艺技术，已广泛应用于各类油气储集层改造，并取得显著效果。但现有水力压裂模型在应用时均存在一定的局限性，不适用于复杂结构井或复杂储集层[1-2]，限制了水力压裂技术的发展。裂缝高度作为水力压裂二维模型的输入参数，以及三维模型的输出结果，是水力压裂模型精确求解的重要影响因素。水力压裂缝高的计算是水力压裂裂缝模型研究的核心问题[3-4]，尤其在当前以页岩气为代表的非常规油气资源需要大规模压裂开发的技术背景下[5-7]，能否准确预测和控制裂缝缝高已经成为压裂施工成败与否的关键。对于埋深较浅、地层应力水平不高的页岩储集层，现有缝高模型都表现出较好的适用性[8]；而对于深部高应力多分层的复杂地层，水力裂缝的缝高往往很难预测[9-10]，亟需一种准确计算此类地层水力压裂缝高的新方法。

在高应力多分层的复杂地层压裂时，裂缝缝高的生长受多种因素制约，包括层间界面及其剪切强度、施工压力、压裂液漏失、天然裂缝发育情况、压裂液密度和黏度等[11-16]。尽管多种因素影响复杂地层中的裂缝高度生长，但在某一泵注压力下，裂缝高度的增长值存在上限，即平衡高度理论[17]，当裂缝上部和下部尖端的应力强度因子小于裂缝上部和下部尖端所处地层岩石的断裂韧性时，裂缝尖端不会增长；否则裂缝尖端增长，裂缝高度增加。

自20世纪70年代，学者们建立了多种用于计算水力压裂裂缝高度的模型。Simonson等[18]建立的水力压裂缝高预测模型将地层分为对称的上下 3层，要求上覆岩层与下部岩层岩石物性相同，这与实际压裂地层环境差别较大，模型实用性较差。Ahmed[19]、Newberry 等[20]和 Economides等[21]对 Simonson 模型进行修正，将地层分为非对称的 3层且上覆岩层与下部岩层岩石物性不同，增强了模型的实用性。Fung等[22]考虑不同地层的岩石物性不同，建立了包含 6层地层的压裂缝高模型，该模型假定裂缝沿高度方向内部净压力恒定。Economides等[23]建立的压裂缝高预测模型考虑了裂缝沿高度方向的内部净压力变化。Weng等[14]对Economides的模型进行了修正，进一步完善了压裂缝高预测模型。Liu等[24-25]建立了更为严谨的水力压裂缝高数学模型（MFEH），首次解决了适用于任意层数地层条件下的水力压裂裂缝高度计算问题。

以往对水力压裂缝高模型的研究均没有考虑裂缝尖端塑性区对缝高延伸的影响。本文在前人研究的基础上，考虑水力裂缝扩展过程中裂缝尖端塑性区的影响并对裂缝扩展高度进行修正，建立全新的水力压裂缝高计算模型。研究成果更好地完善了水力压裂缝高求解的理论方法，为高应力多分层的复杂地层压裂缝高计算和预测提供了理论依据。

1 裂缝尖端塑性区特征及等效裂缝求解

水力压裂裂缝尖端区域存在明显的应力集中现象[26-28]。在高应力作用下，裂缝尖端的岩石会由弹性向塑性转变，当岩石性质表现为塑性时，裂缝尖端的应力强度因子无法使用经典断裂力学理论模型进行计算，裂缝实际的扩展情况发生改变。如图1所示，若不考虑裂缝尖端塑性区域应力集中的影响，裂缝的左右端点分别为A1和B1，对应的裂缝高度为2a；若考虑裂缝尖端塑性区域应力集中的影响，裂缝的左右端点最终能够延伸到A2和B2，对应的裂缝高度为2(a+e)，裂缝的高度发生明显的改变。

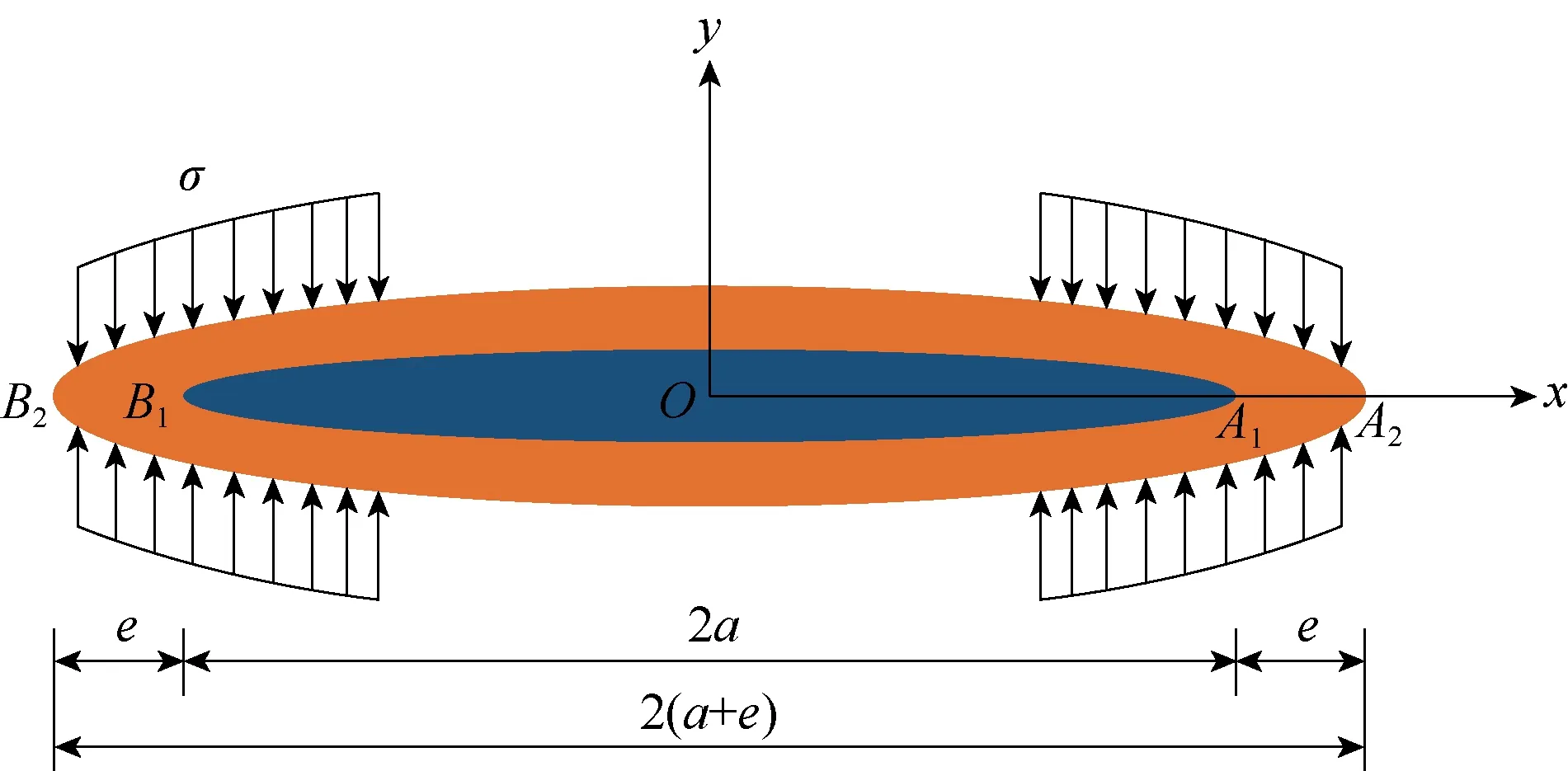
图1 Dugdale等效裂缝高度模型[29]

为了进一步说明裂缝尖端塑性区应力集中对缝高的影响，给出平面应变条件下裂缝尖端塑性区分布计算模型及考虑塑性区应力影响的等效裂缝高度计算方法。根据断裂力学理论，裂缝尖端的应力强度因子为[30]：

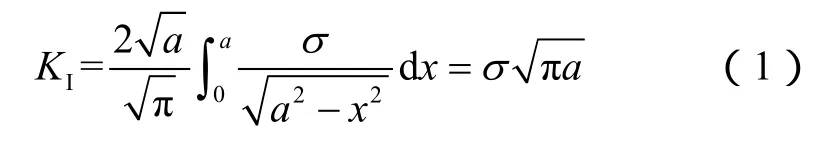
裂缝端部任一点的3个主应力为[31-33]：

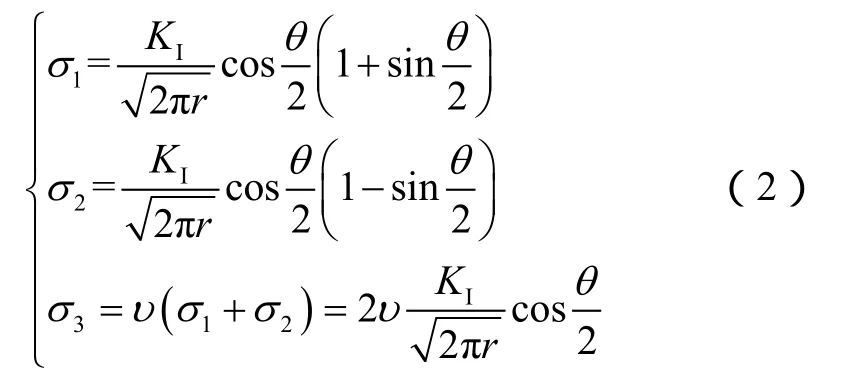
岩石材料服从Mises屈服条件式[34]：

将（2）式代入（3）式中，可得到塑性区边界极坐标形式的曲线方程为：

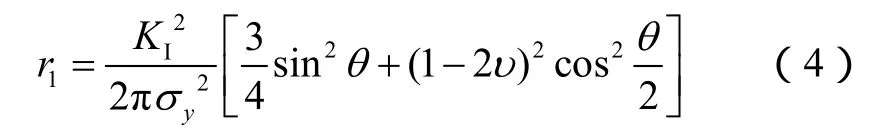
考虑裂缝扩展高度对裂缝尖端应力强度因子KI的影响，通过（4）式分析裂缝尖端塑性区域分布的变化。应用MATLAB编程，确定裂缝高度分别为5，15，35，55 m时产生的塑性区域（见图2）。由图可知，随着裂缝高度的增大，裂缝尖端产生的塑性区逐渐增大。当裂缝高度为5 m时，裂缝尖端仅产生微小的塑性区域；当裂缝高度为55 m时，产生的塑性区高度为2.3 m，达到当前裂缝高度的4.18%。因此在不同缝高下裂缝尖端确实存在塑性区应力集中的影响，且裂缝缝高较大时，裂缝尖端塑性区分布范围大，必然会对裂缝缝高的延伸产生显著影响。所以计算缝高时，需要考虑裂缝尖端塑性区应力集中及其对缝高延伸的影响。

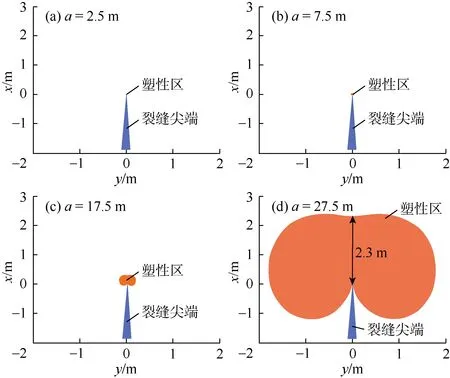
图2 不同裂缝半高条件下裂缝尖端塑性区分布

Dugdale[29]提出裂缝端部产生塑性区后可以用一个等效裂缝代替，如图1所示。原裂缝A1B1高为2a，等效裂缝A2B2的高度为 2(a+e)，其中，e为塑性区尺寸。塑性区内裂缝实际并没有张开，塑性区任一点的应力分量均为σy。由于A1A2段和B1B2段未裂开，所以等效裂缝端点A2及B2处的应力强度因子为零。在塑性区内等效裂缝面间相互作用着均匀分布的拉应力σy，σy产生的应力强度因子K′为负数，因为它的作用是使裂缝闭合。K′的绝对值等于外载作用下的应力强度因子K′：

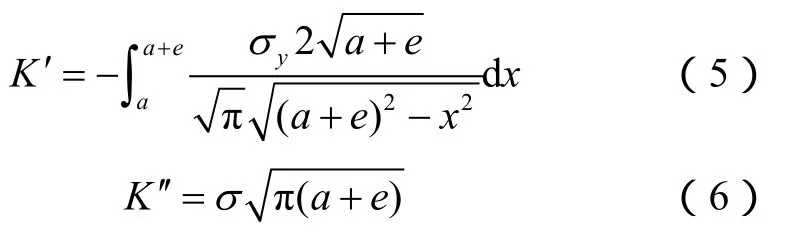
（5）式积分后得：

（9）式为考虑塑性区应力集中影响后，裂缝尖端在缝高延伸方向上产生的塑性区尺寸，即裂缝扩展所产生的附加高度，在此基础上可以对裂缝尖端实际应力强度因子进行计算，从而确定裂缝高度。

2 水力压裂缝高模型

2.1 缝高模型的推导

建立地层中垂直裂缝的缝高物理模型（见图3），图中只展示了垂向上 6个不同性质的地层，但建立的缝高模型不受地层层数限制，可应用于任意层数地层的缝高计算。

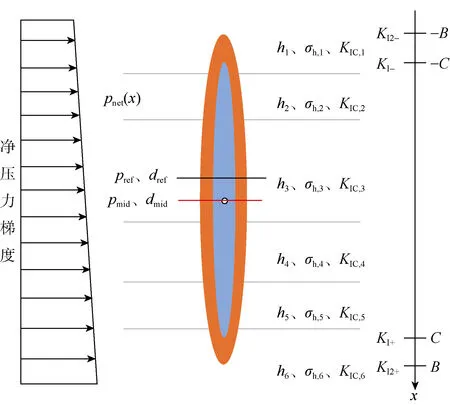
图3 裂缝垂向延伸物理模型

为建立缝高模型进行如下假设：①地层岩石为线弹性介质；②假定流体在整个裂缝高度上起作用；③裂缝扩展区离井筒位置足够远；④水力裂缝的长度远远大于裂缝高度；⑤裂缝高度在裂缝尖端的扩展始终处于平衡状态；⑥裂缝内垂直方向的压力分布满足静水压力，不考虑流体在裂缝中流动的压降。

不考虑裂缝尖端产生的塑性区影响时（图3蓝色区域），参考Liu等[24-25]的模型，裂缝上、下端的应力强度因子可以分别表示为：

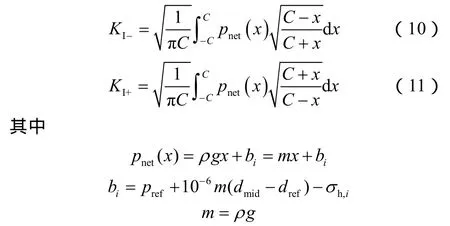
考虑裂缝尖端产生的塑性区影响时（图3橙色区域），裂缝下端塑性区使裂缝闭合的应力σh,i产生的应力强度因子为负值，其绝对值大小与裂缝内压作用下的应力强度因子KI2+相等，根据（11）式得：

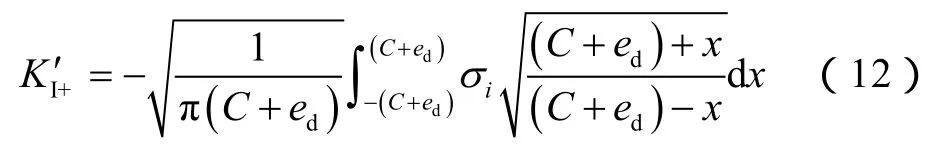
积分后得：

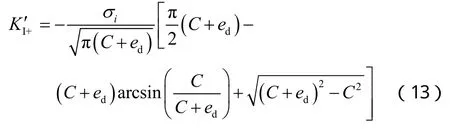
考虑裂缝尖端塑性区影响时，参考（11）式得到裂缝下尖端的应力强度因子：

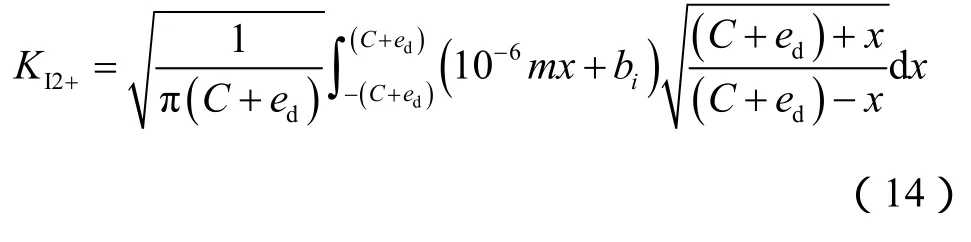
积分后得到：

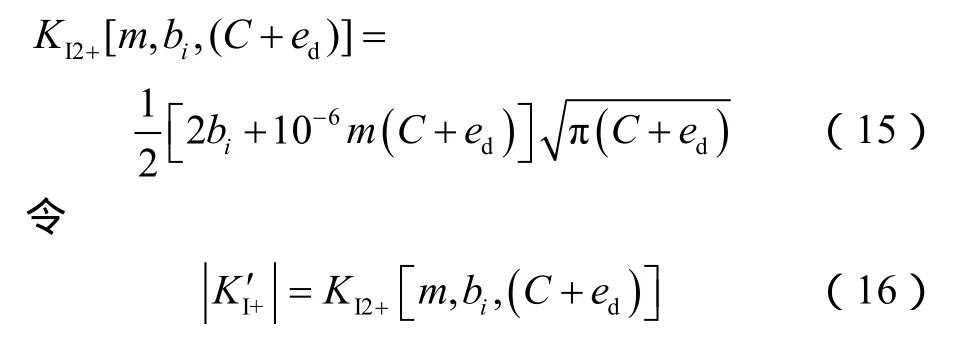
简化可得：

同理可对裂缝上尖端的缝高进行推导得：

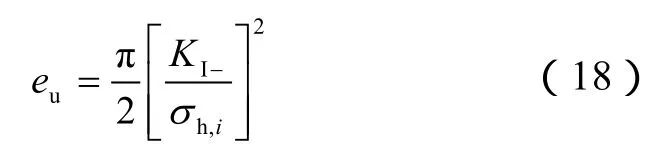
假设A=2C+ed+eu，B=A/2。当考虑裂缝尖端塑性区时，垂直裂缝上、下端的应力强度因子分别表示为：

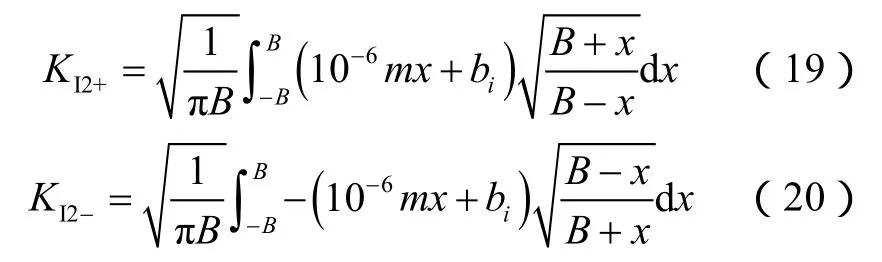
对其进行积分可得到考虑缝尖塑性区影响的水力压裂裂缝上、下端的应力强度因子。裂缝上任意位置x所对应的裂缝下端应力强度因子为：

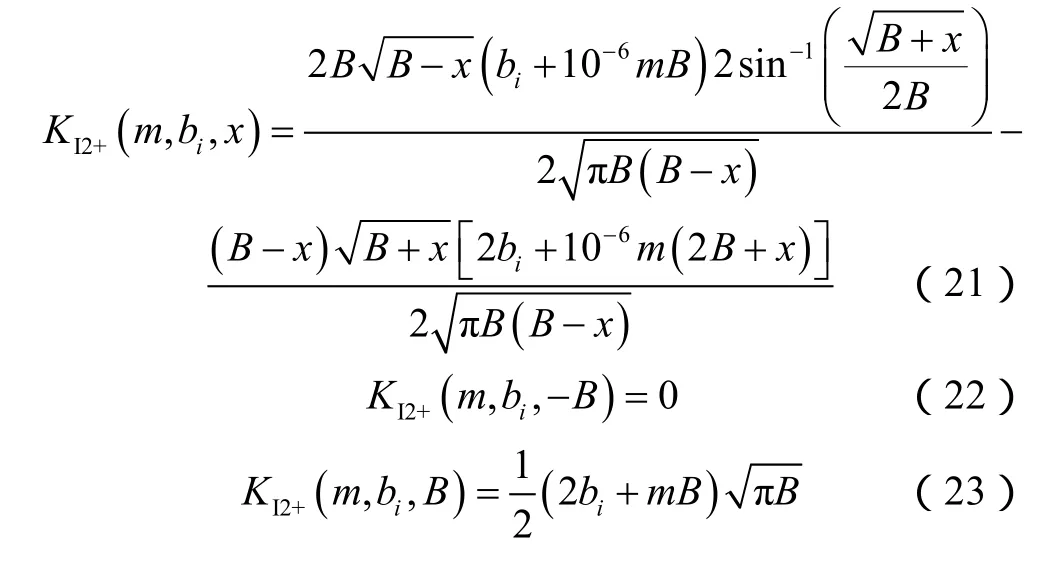
考虑裂缝端部塑性区影响时，在第i层地层的裂缝下端的应力强度因子为：

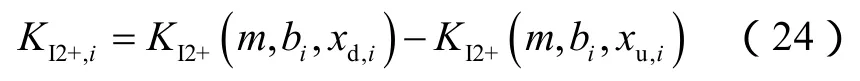
裂缝在多层地层延伸过程中裂缝下端的总应力强度因子为：

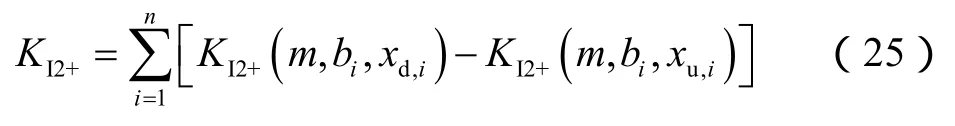
同理可以得到裂缝上端的总应力强度因子为：

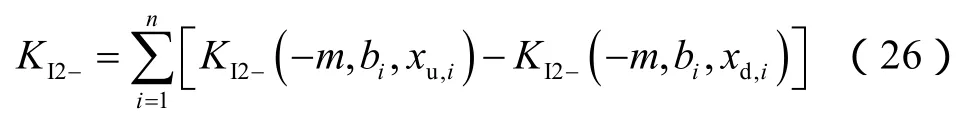
考虑裂缝端部塑性区影响时，裂缝上端延伸条件为KI2-≥KIC,i；裂缝下端延伸条件为KI2+≥KIC,i。

2.2 缝高模型求解方法

水力压裂缝高模型求解时，输入各层的物理参数，计算出不考虑裂缝尖端塑性区影响时的裂缝上下尖端应力强度因子KI-和KI+，计算塑性区高度ed、eu，积分计算考虑塑性区影响的尖端应力强度因子KI2-和KI2+，比较KI2-、KI2+与地层岩石断裂韧性KIC,i的大小。如果KI2-、KI2+小于KIC,i，裂缝缝高停止扩展，求出B；如果KI2-、KI2+大于KIC,i，裂缝缝高继续扩展，进一步累计积分求得KI2-、KI2+，直到满足KI2-、KI2+小于KIC,i的条件，裂缝缝高停止扩展，求出半缝高B。

2.3 缝高模型的验证

在相同条件下，将本文模型与 2种行业模型（FracPro、MFEH）的裂缝高度计算结果进行对比，验证本文模型准确性。计算采用费耶特维尔页岩地层参数[24]，地层分为 7层，各层岩石物理力学参数如表1所示，比较3种模型计算得到的缝高。当射孔位置的压裂液压力为31.3 MPa时，MFEH模型计算的缝高为60.61 m，本文模型计算的缝高为66.47 m；当射孔位置的压裂液压力为32.0 MPa时，本文模型计算的缝高为71.24 m，FracPro模型计算的缝高为82.68 m。通过对比可以看出，本文模型计算的裂缝高度高于MFEH模型的计算结果，而低于FracPro模型的计算结果，与行业模型计算结果相当，表明本文模型具有较好的正确性。由于本文模型在MFEH模型基础上考虑了裂缝尖端塑性区的影响，在每次进行缝高修正求解过程中，均需要对原缝高产生的塑性区进行计算，因此模型的运算效率低于MFEH模型。

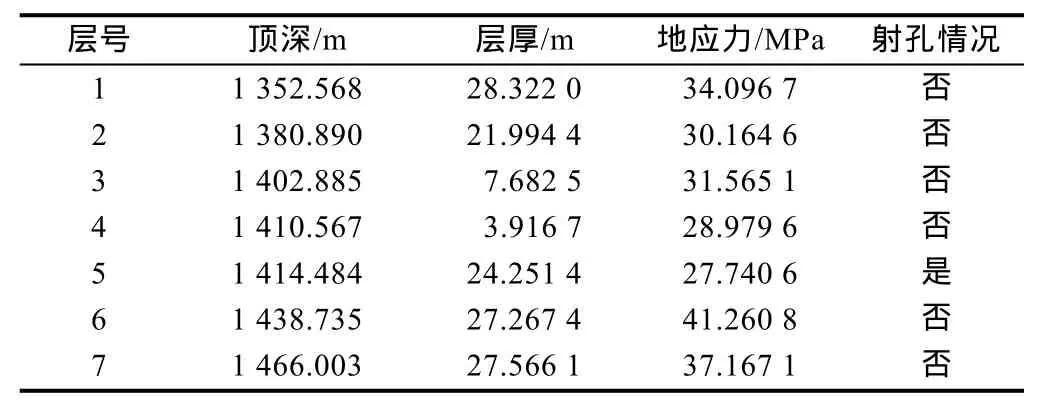
表1 费耶特维尔页岩地层岩石物理力学参数[24]

3 模型实例计算与敏感性分析

基于美国天然气研究中心（GRI）在德克萨斯州哈里森县Waskom油田现场试验数据（见表2），采用本文模型和MFEH模型分别计算水力裂缝缝高变化，地层分为6层，射孔层位于第3层。如图4所示，本文模型计算的缝高变化趋势与MFEH模型计算结果整体较为一致。在裂缝高度较小时，本文模型与MFEH模型的计算结果差异小，当裂缝高度达到较大值后，本文模型计算的缝高呈阶梯状增长。这是因为实际压裂过程中，地层中压裂裂缝的高度并非持续生长，压力达到裂缝增长的延伸压力时，裂缝会突然扩展延伸，导致裂缝内流体压力下降；之后随泵注时间增加，裂缝内流体压力会重新上升，达到裂缝延伸压力后会再次发生裂缝扩展，所以裂缝高度呈现阶梯状增长。另外，从对比结果也可以看出，本文模型计算的裂缝缝高在射孔位置的压裂液压力为50.51 MPa时突破顶层界面，而MFEH模型计算的裂缝高度在射孔位置压裂液压力为52.21 MPa时才突破顶层界面，表明如果不考虑裂缝尖端塑性区应力集中的影响，可能会低估裂缝高度生长的能力，在实际压裂施工中会导致裂缝穿层，从而压漏上部地层，造成严重的压裂事故。

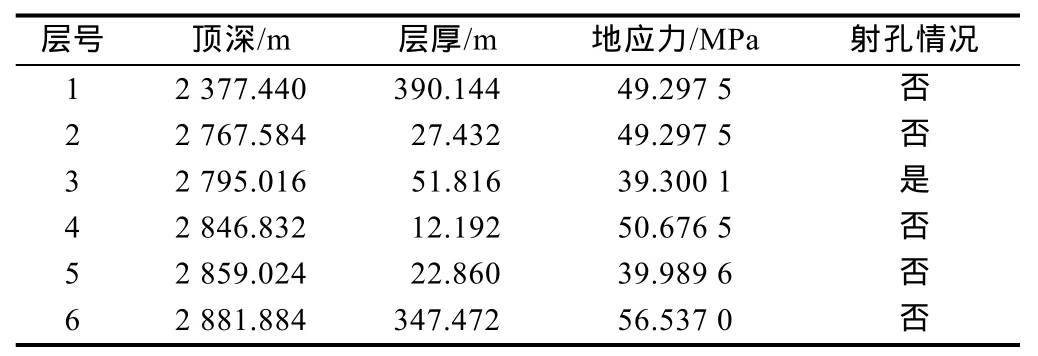
表2 GRI现场试验数据[35]

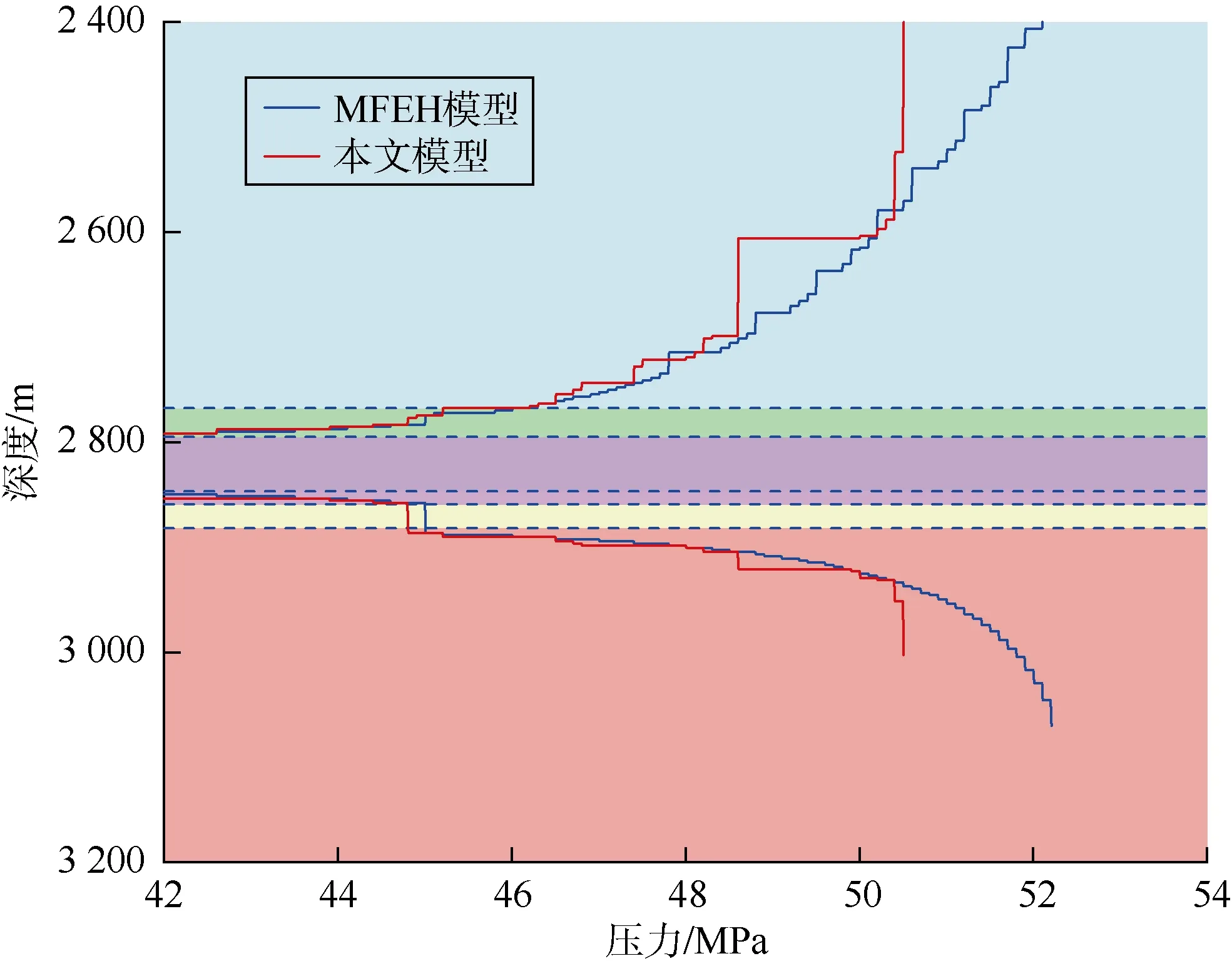
图4 与MFEH模型计算的缝高剖面对比图

3.1 下伏地层地应力对裂缝缝高生长的影响

为了研究下伏地层地应力对水力裂缝缝高生长的影响，将下伏地层地应力（σh,6）设置为35，45，55，65 MPa，绘制不同下伏地层地应力下的缝高变化曲线（见图5）。当下伏地层地应力小于等于45 MPa时，由于第5层、第6层地应力相对较小，射孔位置压裂液压力达到44.81 MPa时，裂缝下尖端迅速扩展到达下边界；当下伏地层地应力大于等于55 MPa时，裂缝下尖端扩展困难。当下伏地层地应力达到65 MPa后，裂缝在下伏地层延伸有限，缝高生长止于第5层、第6层地层界面附近，呈现出憋压阶梯生长的形态。总体上随着下伏地层地应力的增加，裂缝向下端扩展越来越难。

3.2 上覆地层地应力对裂缝缝高生长的影响

分别将上覆地层地应力（σh,1）设置为35，45，55，65 MPa，应用本文模型计算并绘制水力裂缝高度生长曲线（见图6）。上覆地层地应力为35 MPa时，由于地应力相对较小，对裂缝阻挡效果较差，射孔位置压裂液压力达到46.21 MPa时，裂缝上尖端失稳，缝高迅速增长达到顶部界面（见图6a）。随着上覆地层地应力的增加，裂缝上尖端生长越来越困难。上覆地层地应力达到55 MPa时，裂缝上尖端已经无法突破到达顶部界面；当上覆地层地应力达到65 MPa时，裂缝上尖端难以进入上部地层，呈现较为平坦的生长形态，缝高扩展维持在第1层、第2层界面处，裂缝主要向下部地层延伸，突破地层底界面。

3.3 下伏地层岩石断裂韧性对裂缝缝高生长的影响

分别将下伏地层岩石的断裂韧性（KIC,6）设定为0.5，5.5，10.5，15.5 MPa·m1/2，应用本文模型计算相应水力裂缝高度。如图7所示，随着下伏地层岩石断裂韧性的增大，裂缝缝高的生长变化并不明显，所以下伏地层岩石断裂韧性对裂缝高度扩展的影响较小，增加下伏地层岩石断裂韧性只能在一定程度上抑制裂缝缝高的扩展。

3.4 上覆地层岩石断裂韧性对裂缝缝高生长的影响

分别将上覆地层岩石断裂韧性（KIC,1）设为0.5，5.5，10.5，15.5 MPa·m1/2，应用本文模型计算水力裂缝高度。如图8所示，当上覆地层岩石断裂韧性很小时，裂缝容易突破上部地层到达地层顶界面。随着上覆地层断裂韧性的增大，裂缝上尖端的扩展变得困难，裂缝下尖端向下部地层扩展的高度逐渐增大。

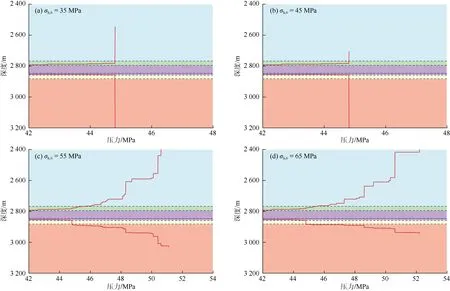
图5 下伏地层地应力对裂缝缝高生长的影响

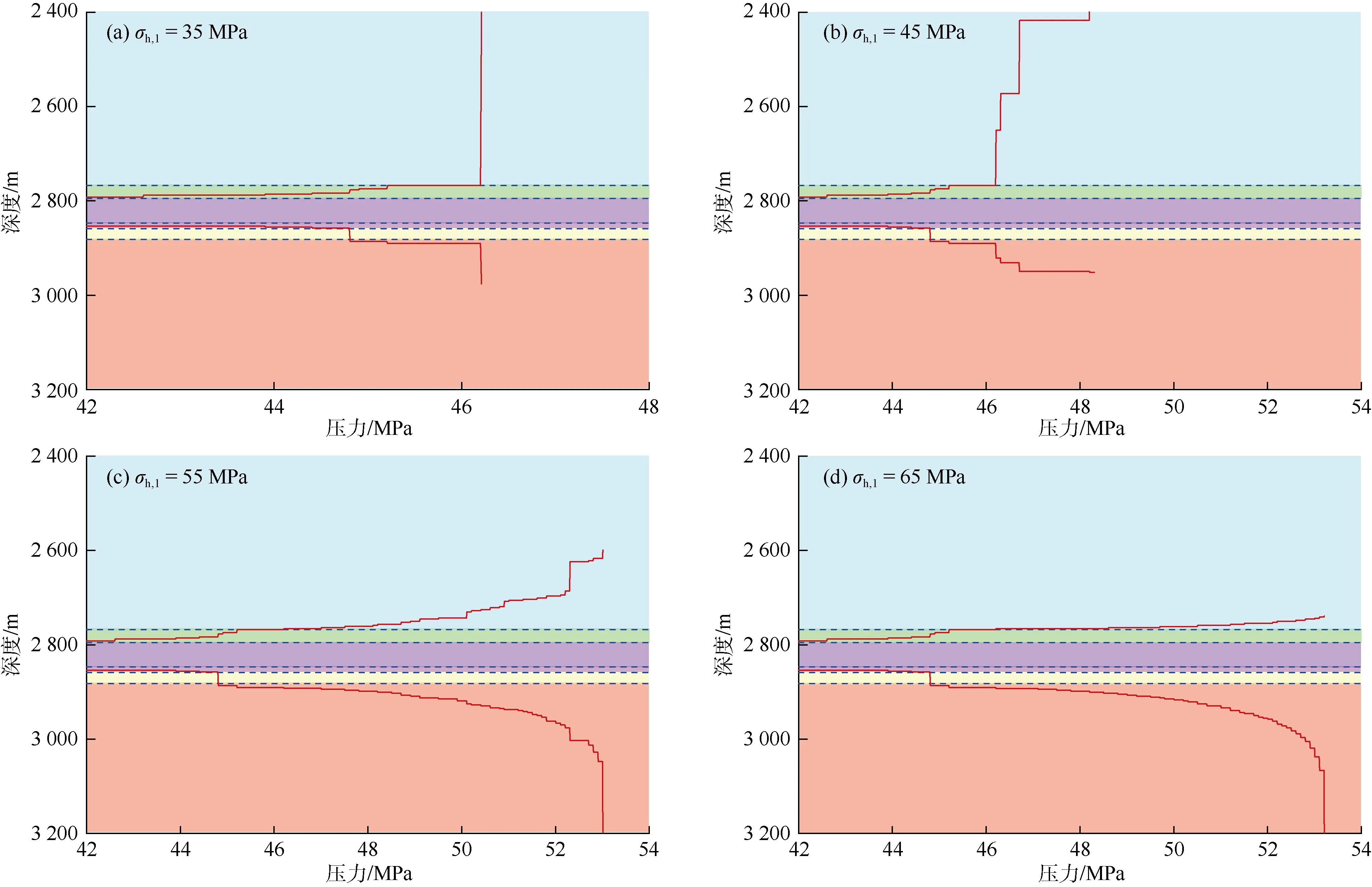
图6 上覆地层地应力对裂缝缝高生长的影响

图7 下伏地层岩石断裂韧性对裂缝缝高生长的影响

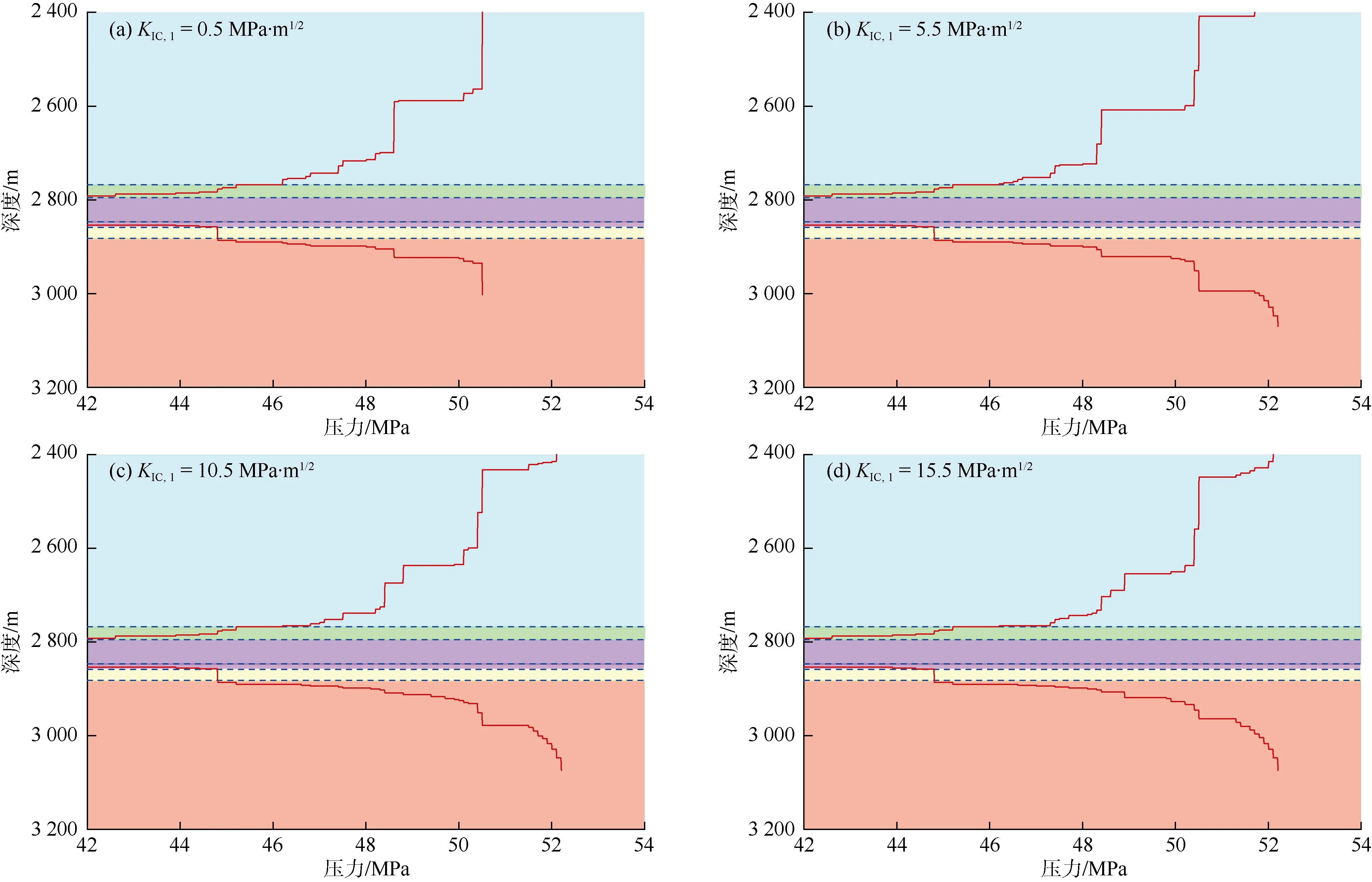
图8 上覆地层岩石断裂韧性对裂缝缝高生长的影响

3.5 断裂韧性与地应力的共同作用对裂缝缝高生长的影响

为了研究断裂韧性和地应力的共同作用对裂缝缝高生长的影响，分别设计了高地应力低断裂韧性和低地应力高断裂韧性两种情况。对于高地应力低断裂韧性地层，分别设σh,2为65 MPa，KIC,2为0.5 MPa·m1/2

和σh,5为 65 MPa，KIC,5为 0.5 MPa·m1/2（见图9a 和图9c）。结果表明当地应力高时，裂缝尖端生长缓慢，即使地层岩石的断裂韧性较小，缝高也没有出现频繁的跳跃生长的失稳现象。对于低地应力高断裂韧性地层，分别设σh,2为 45 MPa，KIC,2为 10.5 MPa·m1/2和σh,5为 45 MPa，KIC,5为 10.5 MPa·m1/2（见图9b 和图9d）。尽管地层岩石断裂韧性比较高，但地应力较小，裂缝高度扩展较快，甚至在裂缝尖端出现了突破和跳跃式失稳增长，说明地层应力对裂缝缝高的生长起主要控制作用，地层岩石断裂韧性只能在一定程度上对高度生长起抑制作用。

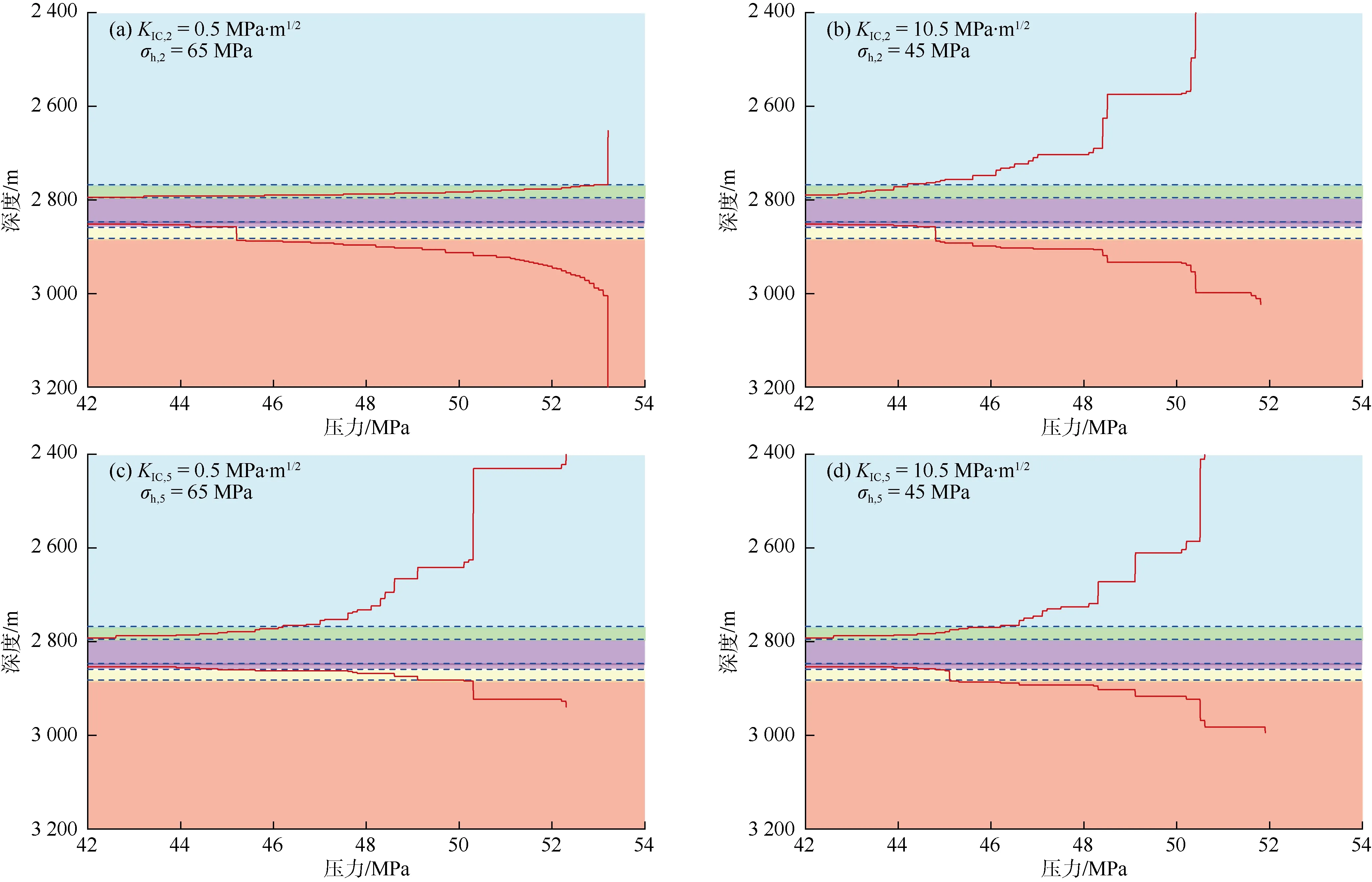
图9 断裂韧性与地应力共同作用对裂缝缝高生长的影响

3.6 上覆地层与射孔层应力差对裂缝缝高生长的影响

将上覆地层（第2层）与射孔层应力差Δσ设置为-8，0，8，16 MPa，应用本文模型计算并绘制裂缝高度生长变化曲线。上覆地层与射孔层应力差为-8，0 MPa时，上覆地层地应力小于等于射孔层的地应力，地应力对裂缝缝高生长无法起到阻挡作用，在射孔层裂缝起裂后，裂缝缝高扩展突破射孔层和上覆地层（见图10a和图10b）。随着上覆地层地应力增加，上覆地层地应力大于射孔层地应力，应力差逐步增大，裂缝向上覆地层的扩展变得困难，较于图10a和图10b，裂缝在上覆岩层中增长相对缓慢（见图10c和图10d）。上覆地层与射孔层应力差的增加，有效阻止裂缝缝高向上延伸，对裂缝缝高生长起到了明显的抑制作用。

3.7 压裂液密度对裂缝缝高生长的影响

分别设定压裂液密度为 1.0×103，1.2×103，1.4×103，1.6×103kg/m3，计算分析压裂液密度对裂缝缝高生长的影响（见图11）。随着压裂液密度的增大，裂缝内压裂液的重力增大，作用在裂缝下端的净压力数值将大于裂缝上端，且密度越大，裂缝上下端净压力差值越大，使裂缝上尖端的生长减缓，下尖端生长加快，从而影响整个裂缝高度形态；当压裂液密度较小时，裂缝上下端净压力差值较小，即应力强度因子差别小，通常上部地层地应力逐渐减小，岩石压实变差，断裂韧性也减小，裂缝缝高容易向上部地层延伸到达地层顶界面。这对于实际压裂施工具有很好的指导意义，如想控制裂缝在地层中的缝高延伸，可在一定程度上通过控制压裂液密度来实现，通过设置合适的压裂液密度来控制裂缝下端和上端在地层中的延伸。

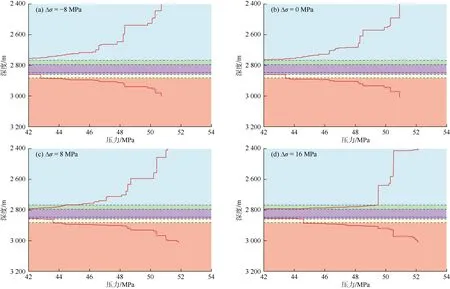
图10 上覆地层与射孔层应力差对裂缝缝高生长的影响

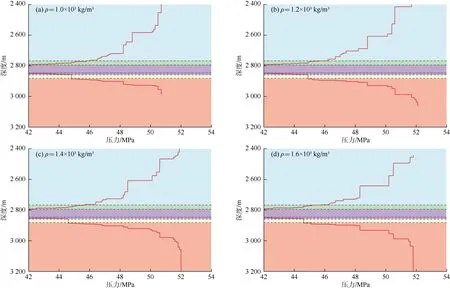
图11 压裂液密度对裂缝缝高生长的影响

3.8 讨论

由上述计算实例可以看出，地层的应力条件、地层岩石断裂韧性以及压裂液密度等因素对裂缝的缝高扩展均存在不同程度的影响，应用本文建立的缝高求解模型能够对高应力多分层地层的压裂缝高进行计算和预测。但在建立缝高求解模型时，为了简化计算，忽略了一些因素对缝高扩展的影响，如裂缝中流体在缝高方向的流动压降，和地层岩石断裂韧性受地应力以及裂缝扩展的影响。今后仍需开展相关研究来进一步完善本文缝高模型，使该模型更好地应用于现场压裂的缝高计算和预测。另外，本文模型主要研究了不同条件下裂缝内压裂液压力对裂缝高度生长的影响，并没有建立裂缝延伸的三维模型，所以无法实现裂缝长度和高度生长的耦合计算。

4 结论

水力压裂的裂缝缝高在生长过程中，会呈现出阶梯生长的扩展形态，且裂缝缝高越大，阶梯生长的现象越明显。地应力对水力裂缝缝高的扩展有重要影响，当地应力较小，即本文实例中下伏地层地应力或上覆地层地应力低于45 MPa时，裂缝尖端容易发生失稳扩展，缝高迅速增长；而随着地应力的增加，下伏地层地应力或上覆地层地应力达到55 MPa时，裂缝缝高扩展变得越来越困难。地应力对裂缝缝高的生长起主要控制作用，地层岩石断裂韧性只能在一定程度上对裂缝高度生长起到抑制作用。压裂液密度的增大有利于裂缝下尖端的扩展，当压裂液密度低于1.2×103kg/m3时，裂缝缝高容易向上部地层延伸，随着压裂液密度的增大裂缝缝高则主要向下部地层延伸。

符号注释：

a——水力裂缝半高，m；B——考虑塑性区影响的裂缝半高，m；C——未考虑塑性区影响的裂缝半高，m；dref——射孔位置垂直深度，m；dmid——裂缝中部垂直深度，m；e——塑性区尺寸，m；g——重力加速度，m/s2；hi——第i层地层的厚度，i=1，2，…n，m；KIC——地层岩石断裂韧性，MPa·m1/2；KI——应力强度因子，MPa·m1/2；K′——塑性区内等效裂缝面间拉应力产生的应力强度因子，MPa·m1/2；K′——考虑裂缝尖端塑性区影响时裂缝尖端的应力强度因子，MPa·m1/2；KI-——不考虑缝尖塑性区影响时裂缝上尖端应力强度因子，MPa·m1/2；KI+——不考虑缝尖塑性区影响时裂缝下尖端应力强度因子，MPa·m1/2；KI2-——考虑塑性区影响后上尖端应力强度因子，MPa·m1/2；KI2+——考虑塑性区影响后下尖端应力强度因子，MPa·m1/2；KI′+——裂缝下端塑性区使裂缝闭合的应力产生的应力强度因子，MPa·m1/2；n——总地层数；pmid——裂缝中部的压裂液压力，MPa；pnet——裂缝内任一点流体净压力，MPa；pref——射孔位置的压裂液泵注压力，MPa；r——裂缝端部塑性区内任一点到裂缝端部的距离，m；r1——裂缝端部塑性区半径，m；x——水力裂缝缝高扩展方向，m；y——水力裂缝缝宽扩展方向，m；θ——以裂缝端部为极坐标端点，到塑性区任一点逆时针转过的极角，（°）；υ——岩石泊松比，无因次；ρ——压裂液密度，kg/m3；σ——分布载荷，MPa；σy——裂缝面间相互作用的拉应力，MPa；σh,i——第i层地层的水平最小主应力，i=1，2，…，n，MPa；σ1，σ2，σ3——裂缝端部任一点的3个主应力，MPa。下标：i——第i层地层；d——下端；u——上端。