水平井分段压裂平面三维多裂缝扩展模型求解算法

陈铭，张士诚，胥云，马新仿，邹雨时

（1.中国石油大学（北京），北京 102249；2.Texas A & M University，College Station 77840，USA；3.中国石油勘探开发研究院，北京 100083；4.中国石油油气藏改造重点实验室，河北廊坊 065007）

0 引言

水平井分段多簇体积改造是非常规油气开发的关键技术[1-3]。为提高储量动用程度，北美油公司不断探索缩小井距与缝间距的体积改造技术[4]。现场光纤温度监测与声监测表明[5]，小间距改造情况下，多簇裂缝存在不均衡进液等问题，同时各簇进液比例与射孔参数、各簇地应力分布等因素紧密相关。为提高多簇裂缝均衡扩展程度、优化多簇压裂方案设计，急需建立一种耦合“井筒-射孔-裂缝”的多裂缝扩展高效模拟方法[6]。

裂缝扩展模型包括二维、拟三维、平面三维和全三维模型[6]。二维模型以PKN（Perkins-Kern-Nordgren）和KGD（Khristianovich-Geertsma-Daneshy）模型为代表，适用于恒定缝高的单缝扩展。拟三维模型包括椭圆模型与基于PKN单元的模型。椭圆模型假设裂缝由以射孔为中心的上下半椭圆构成，裂缝形态仅需要由椭圆长轴、短轴和离心率确定[7]。基于PKN单元的拟三维模型引入缝高解析解计算裂缝高度，流动仍为沿缝长的一维流动，计算量较小，但在射孔段为高应力、薄互层等情况下缝高误差较大[8]。Kresse等[9]提出的非常规裂缝模型即为拟三维模型在多裂缝扩展中的应用。赵金洲等[10]提出了基于拟三维模型的多裂缝扩展模型，并建立了射孔优化方法。拟三维模型在多簇应力干扰计算方面仍是一种二维模型方法，难以对应力干扰下缝高扩展进行准确模拟[11]。为准确分析裂缝形态，Advani[12]、Barree等[13]提出平面三维模型。平面三维模型采用三维固体方程计算岩石变形，通过裂缝边界确定裂缝长度和高度。Peirce等[14]引入尖端解析解，提出了平面三维模型的隐式水平集算法。Dontsov等[15]提出尖端统一解析解，并应用于隐式水平集算法[16]。Chen等[17]采用隐式水平集算法对比了拉链式压裂与同步压裂的裂缝扩展形态。为描述水力裂缝空间扭转问题，Carter等[18]提出了全三维模型，全三维模型可计算裂缝空间扭转，计算量巨大。Xu等[19]实现了平面偏转的分段多簇压裂模拟，并研发了FrackOptima软件。全三维模型目前工业应用尚未见报道，主要困难是理论上空间扭转裂缝的判断准则还不完善[20]，同时计算量巨大，不利于工程应用。此外，近几年研究者也提出了天然裂缝发育地层的复杂裂缝扩展模型[21-24]。本文重点研究多簇压裂中“井筒-射孔-水力裂缝”耦合流动的多裂缝扩展问题，并分析多簇压裂的射孔设计对策，暂不考虑天然裂缝的影响[10,14,16,25]。

显然，目前在分段多簇压裂设计中最为实用与可靠的压裂模型为平面三维模型。目前广受认可的算法为 Peirce等[14]、Dontsov等[16]隐式水平集算法。该算法采用隐式方法求解多裂缝扩展的流固耦合方程，裂缝边界通过隐式水平集方法判断。隐式解法虽然可以保证计算稳定，但非线性方程组的求解工作量较大，尤其是边界元系数矩阵为稠密矩阵，更加增大了计算量，同时在处理支撑剂运移、裂缝闭合等问题时方程约束增多，进一步增大了求解难度和计算量，不利于工程应用。此外，该算法目前并未考虑射孔摩阻作用，相关工程应用报道也较少[25]。

为此，本文提出一种平面三维模型求解新算法，该算法采用显式积分方法求解裂缝扩展的流固耦合方程，通过最短路径算法与尖端解析解求解裂缝边界。通过与解析解[26]、澳大利亚国家研究院有机玻璃实验[27]、隐式水平集算法[16,28]进行对比，验证算法的准确性与效率。采用浙江油田页岩气水平井实际参数进行算例分析，重点分析簇间应力分布和射孔数分布对各簇进液控制规律及工程对策。

1 数学模型

1.1 基本假设

本文研究多簇压裂工艺的裂缝扩展规律，几何模型如图1所示，每段簇数为nf，裂缝簇序号用k标记。多簇裂缝扩展主要包含 4个物理过程：流体在井筒和裂缝内流动；岩石在流体压力作用下变形；流体向地层滤失；裂缝尖端破裂。本文采用 Peirce等[14]平面三维模型的假设，即滤失符合 Carter滤失模型；缝内流体边缘与裂缝边缘重合；裂缝沿垂直于最小水平主应力方向的平面扩展。Bunger等[29-31]研究表明，多裂缝扩展中偏转并不明显，同时国内非常规油气储集层水平应力差较大，因此平面模型适用。

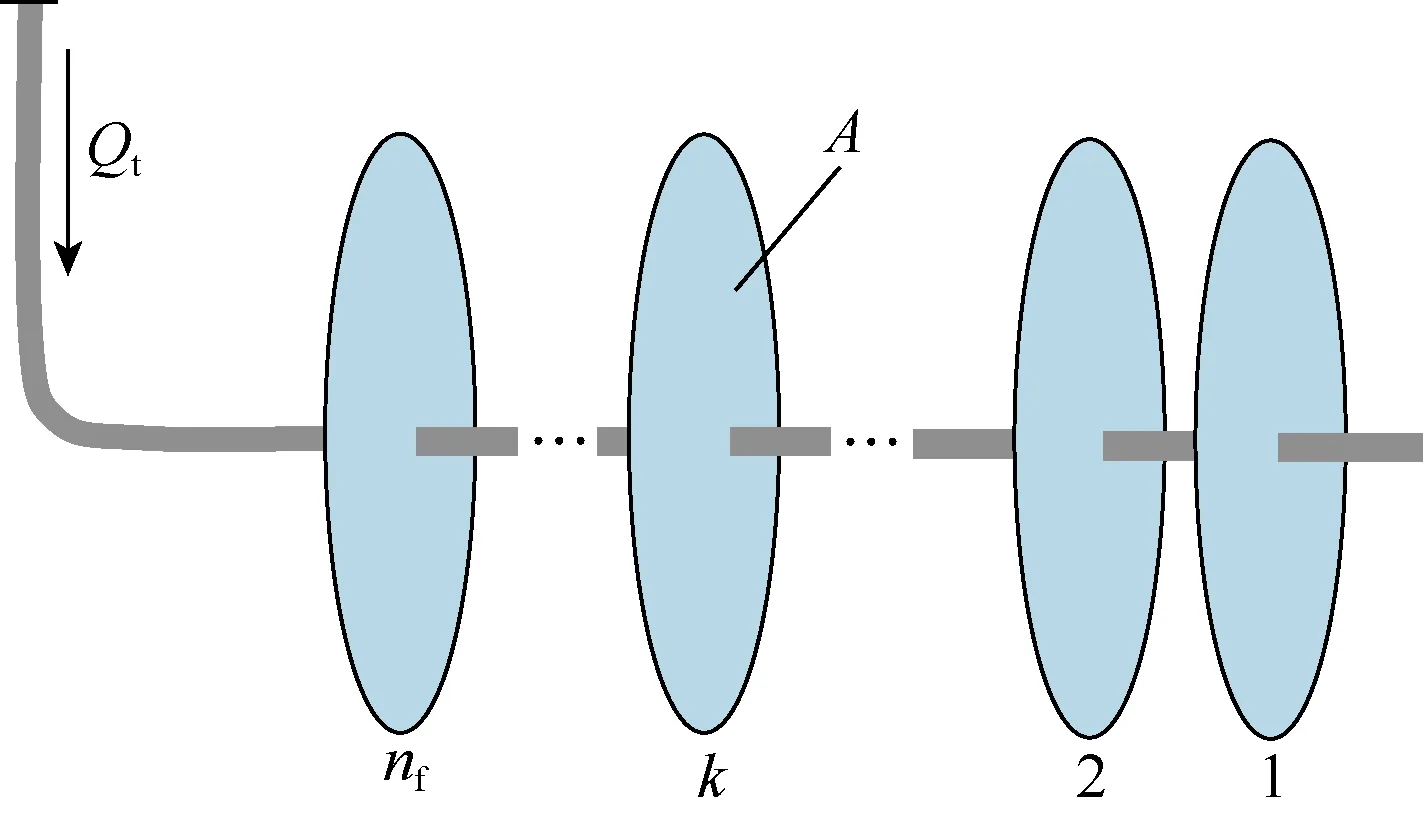
图1 几何模型

1.2 控制方程

1.2.1 固体方程

用固体方程描述流体压力、地应力作用下裂缝宽度的分布。根据无限大地层弹性力学点源解，固体变形的边界积分方程为[14]：

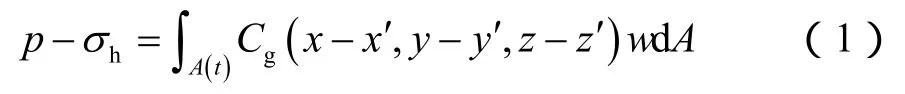
1.2.2 流动方程

①井筒流动方程。井筒内流动摩阻对流量分配影响较小[32]，同时各簇间距较小，因此各簇之间井筒流动摩阻可以忽略。各簇裂缝对应的井底压力满足：

射孔摩阻计算公式为[33]：

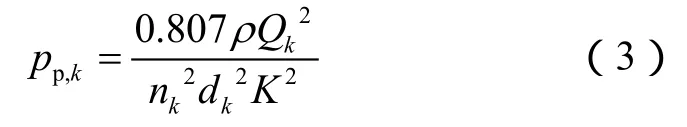
根据流量守恒，各簇流量之和为总注入排量：

②缝内流动方程。对于每簇裂缝，缝内流体遵循泊肃叶流动，即：

考虑流体不可压缩，因此流体连续性方程为：

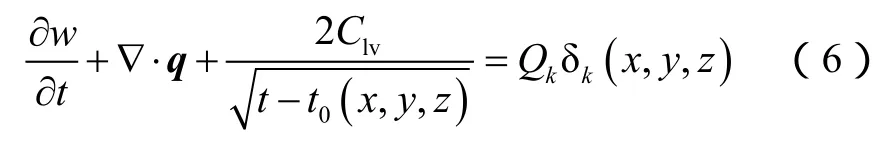
将（5）式代入（6）式，得到流体流动控制方程：

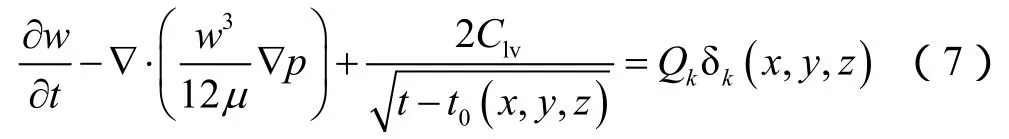
1.2.3 裂缝边界条件

根据断裂力学准则，裂缝尖端达到扩展条件时：

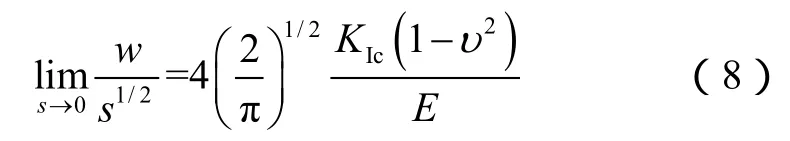
由于裂缝尖端即为流体边缘，因此裂缝边界满足零流量条件，即：

1.2.4 裂缝尖端解析解

断裂力学解仅限于裂缝尖端很小的范围，因此需要非常细的网格才能准确捕捉（8）式所示的尖端条件。为实现粗网格条件下对尖端条件的准确捕捉，本文采用缝尖解析解求解裂缝位置[16]。图2为尖端断裂力学解与解析解的适用范围示意图。

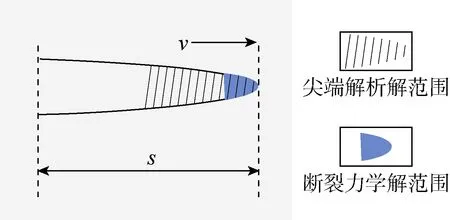
图2 尖端解析解与断裂力学解适用范围示意图

引入无因次量，令：

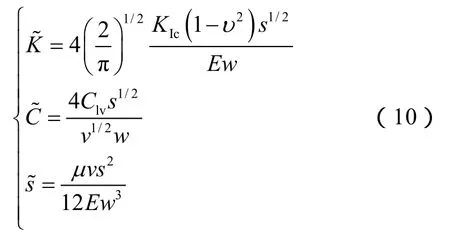
裂缝尖端扩展速度、扩展长度、断裂韧性、弹性模量、滤失系数等均影响裂缝扩展的临界宽度。裂缝尖端扩展时满足方程：

（11）式为裂缝扩展速度、扩展步长与临界宽度的非线性方程。由于δ的变化范围较小，为简化方程求解，采用 Dontsov提出的近似解法，近似解误差在0.3%以内[15]。具体解法如下。

①取δ=0时，得到（11）式的零阶近似：

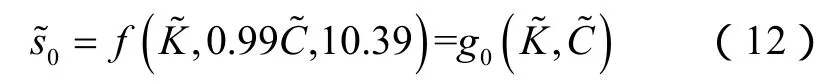
②根据（12）式计算δ：

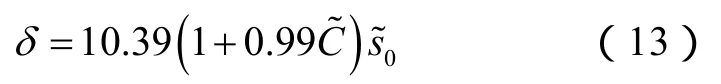
③将（13）式的计算结果代入（11）式，得到修正的零阶近似解：

（14）式为尖端速度、临界宽度、扩展步长的控制方程，该方程适用范围远大于断裂力学解范围，因此可有效增大空间步长，提高计算效率。

2 求解算法

2.1 网格系统

本文采用固定网格计算裂缝扩展。将裂缝平面划分为足够多的矩形单元，单元类型包含 4种：注入点单元、已开启单元、缝尖单元和未开启单元（见图3）。每个时间步需判断缝尖单元是否达到扩展条件，从而更新网格的单元类型。单元中心点为宽度和压力求解点，单元边界为流量求解位置。

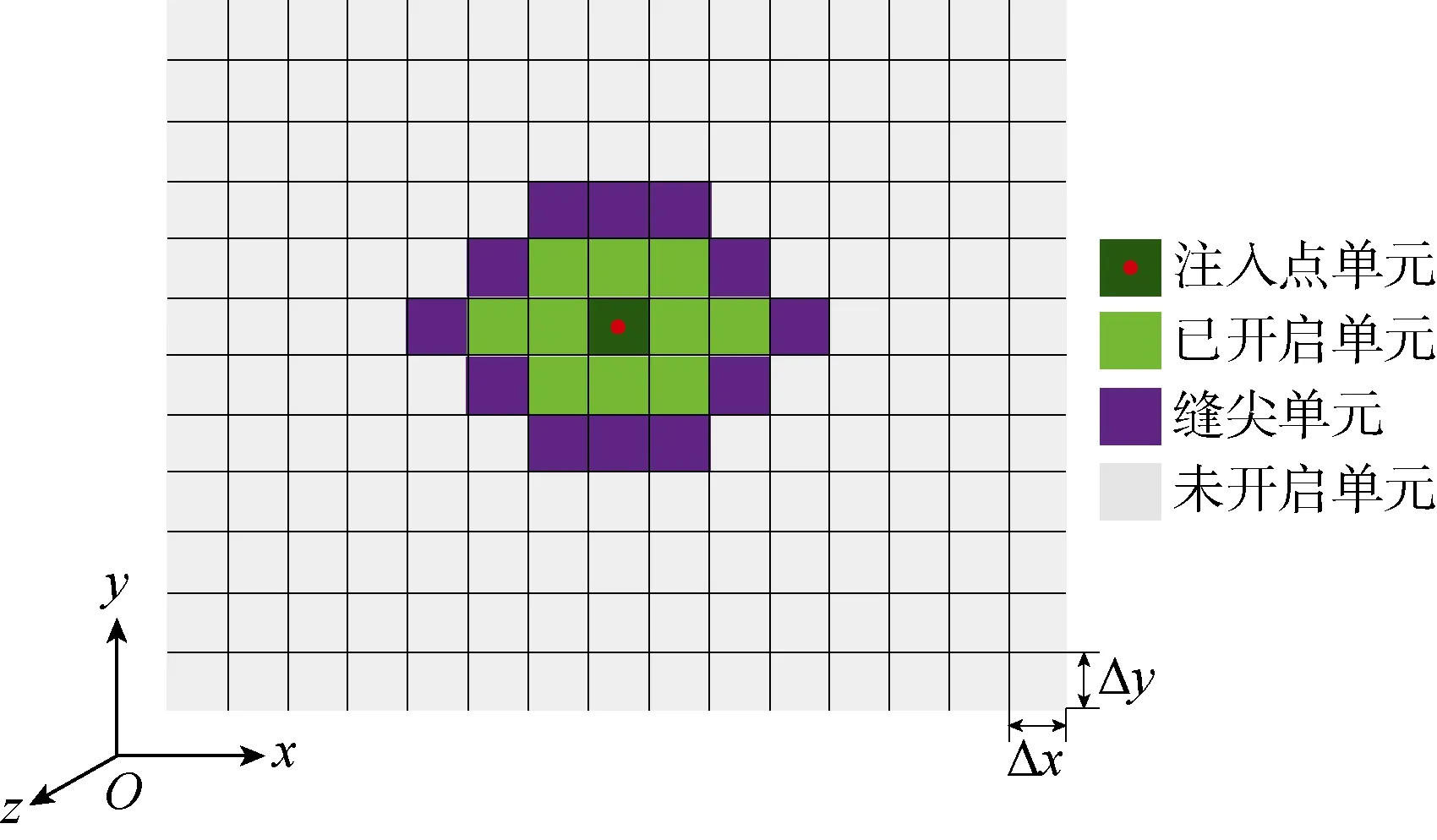
图3 网格系统与单元类型

2.2 离散方程

2.2.1 固体方程的离散

固体方程离散采用常位移不连续法[34]。单元中心点宽度近似为单元宽度，因此边界积分方程的离散形式为

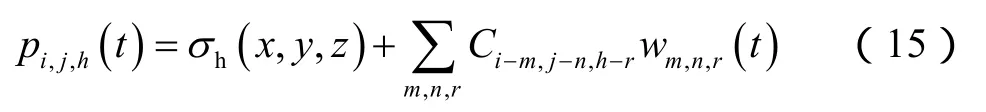
（15）式的矩阵形式为：

2.2.2 流动方程的离散

①缝内流动方程的离散。对控制方程（7）在空间内进行离散，得到流动方程的一阶微分方程形式：

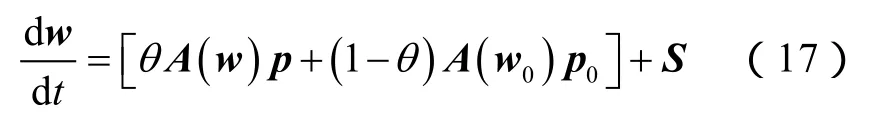
（17）式中，A(w)p与S的分量形式分别为：

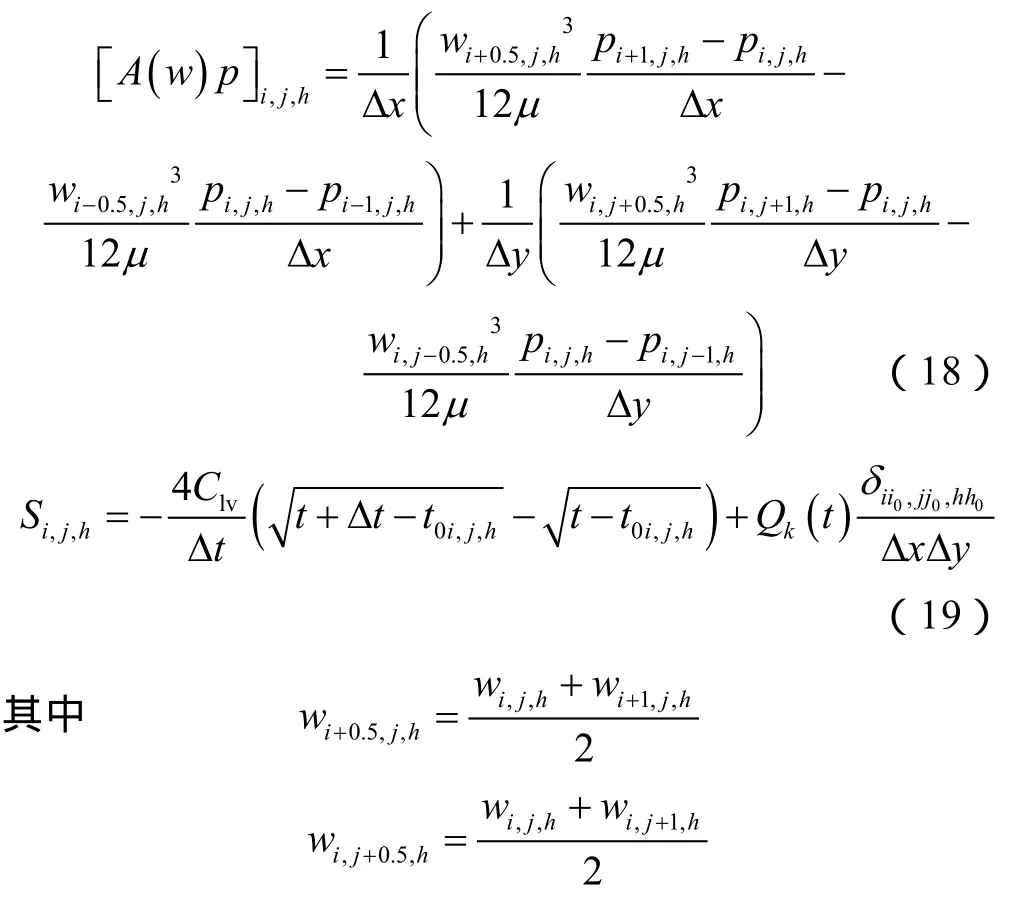
②井筒流动方程的离散。井筒流动方程的离散形式为：

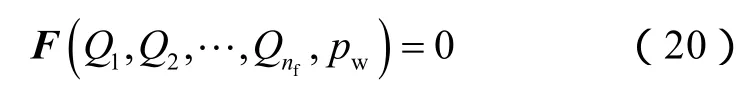
上式为nf+1维非线性方程组，F的分量形式为：

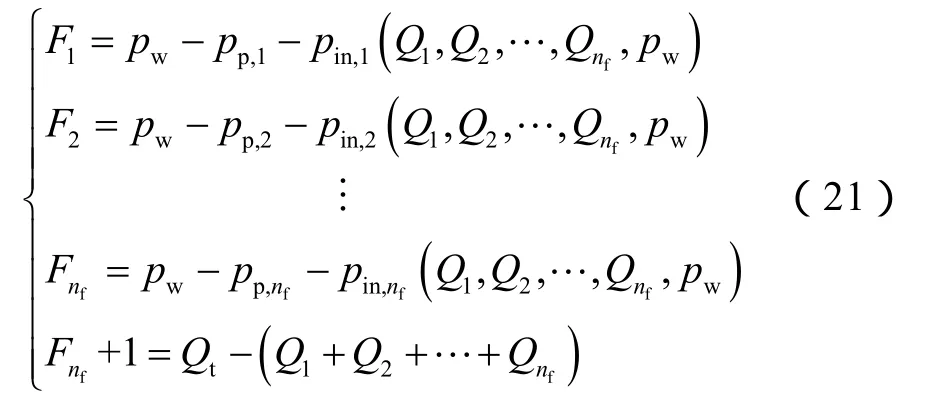
2.3 流固耦合方程

微分方程（17）中θ=0时为显式格式，θ=1时为完全隐式格式。微分方程（17）为刚性方程，显式方法需满足CFL（Courant-Friedrichs-Lewy）条件才能保证计算稳定，因此研究者主要采用隐式方法求解微分方程（17）[6-7]。隐式解法满足无条件稳定性，不需要CFL条件，但隐式方法在流固耦合方程计算中仍然存在问题，主要表现在：①求解方程（17）通常采用牛顿-拉夫逊或不动点迭代方法[6-7]，每次迭代需要解线性方程组。由于固体方程中的影响系数矩阵C为稠密矩阵，因此通常采用直接法解线性方程组。直接法的工作量取决于单元数量，单元数量增大后，时间复杂度巨大。尽管预处理方法可以将工作量降低，但对于单元数量较大情况，时间复杂度仍然巨大[35]。②考虑支撑剂运移或裂缝闭合等非线性问题时，流固耦合方程的约束条件增多，增大了隐式方法求解难度和计算工作量[35]。③为保证计算精度，隐式方法不能采用太大的时间步长[7,28]。

考虑到隐式方法仍存在计算困难和时间成本较高等问题，本文采用显式方法求解方程（17）。为提高显式方法计算效率，采用稳定型 RKL（Runge-Kutta-Legendre）[36]显式积分方法求解方程（17）。该方法采用多步时间积分方法，利用递归式Legendre多项式的稳定性特征，扩大了显式算法的CFL时间步长，因此可显著降低计算量，提高显式算法计算效率。

方程（17）可记为：

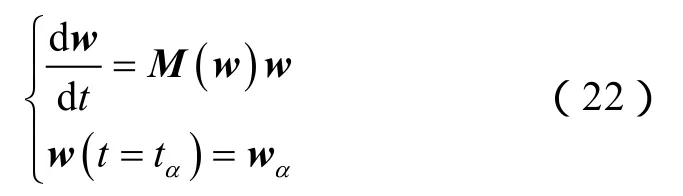
利用Legendre递归多项式绝对值小于1的特征，将单步积分采用S步递归式积分求解。时间项2阶精度的S步 RKL方法的计算格式参照文献[36]确定。S步RKL方法的时间步长满足：

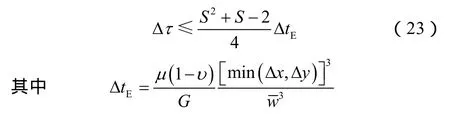
对于裂缝扩展问题，在保证稳定性条件下，确定时间步长时也需考虑计算精度。因此取S步RKL方法的时间步长为：

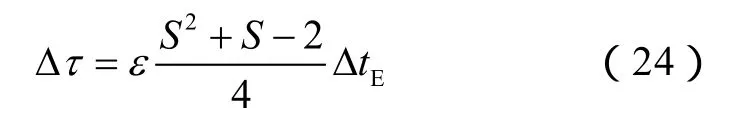
（24）式中ε为松弛系数，0＜ε≤1，经过计算分析，其取0.8可满足足够精度。对于非均质地应力问题，若裂缝扩展进入低应力层后扩展速度加快，需要适度降低松弛因子以避免时间步过大。

2.4 尖端扩展

Peirce等[14]、Dontsov等[16]利用与裂缝尖端相邻的激活单元的解析解计算裂缝尖端位置和尖端宽度。本文显式算法以尖端未开启单元临界宽度和扩展速度计算单元开启状态。每一时间步判断缝尖单元的相邻未开启单元是否达到扩展条件，从而更新单元类型。采用最短时间路径算法确定单元开启时间与是否达到开启条件。需要注意的是，本文仍采用网格激活方式进行裂缝边界捕捉[13]。

以图4为例，对于待开启单元a，相邻单元为b、c、d、e。根据最短路径算法，a单元开启时间为：

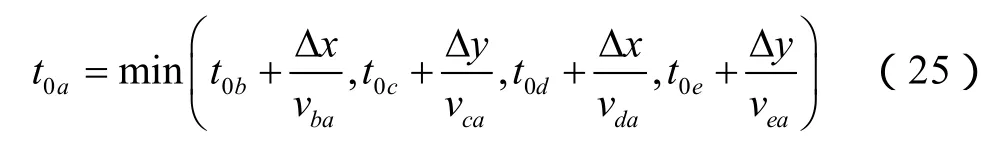
未开启单元的当前开启时间为正无穷大。假设b、c、d单元为未开启单元，e为已开启单元，则a单元开启时间为：

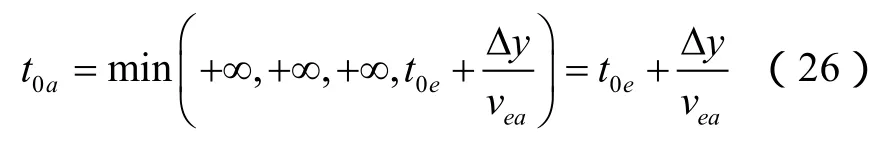
当vea满足尖端扩展条件（11）式时，a单元成为开启单元。

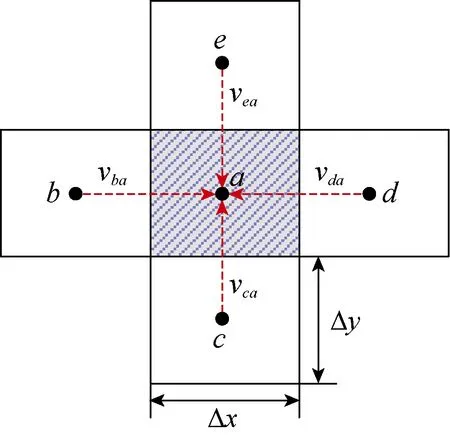
图4 裂缝尖端扩展示意图

2.5 算法

平面三维多裂缝扩展模型算法如下。

①设定注入时间tf，模型输入参数包括：岩石力学参数、注入程序、液体参数、地应力分布等；

②令α=0，t=t0，计算初始宽度w0和压力p0；

③令α=α+1，t=t+Δt，求解（22）式得到当前开启单元的宽度wα和压力pα。若t＞tf，结束计算；

④采用牛顿-拉夫逊方法求解（20）式得到各簇流量分配；

⑤计算当前时刻的待开启单元数，求解（11）式得到所有待定单元的临界宽度，判断是否发生开启，若发生开启，则更新为尖端单元，否则仍为未开启单元；

⑥根据步骤⑤更新单元类型，确定新的裂缝尖端单元和待定单元，返回步骤③。

算法主要包括各簇分流量计算、固体变形与流动耦合方程计算和裂缝扩展边界计算 3个模块。各簇分流量通过牛顿-拉夫逊方法计算，具有二阶收敛速度。固体变形与流动耦合方程的稳定型RKL解法具有二阶时间精度，并满足计算稳定性[36]。裂缝扩展边界采用尖端解析解计算，尖端解析解适用范围可达缝长的10%，而线弹性力学解析解范围仅为缝长的 0.1%～1.0%，因此可在粗网格条件下实现较高计算精度，从而减小计算量[37]。3个模块均满足收敛性和稳定性，因此算法理论上可行。

3 算法验证与效率对比

3.1 准确性验证

3.1.1 与penny裂缝解析解对比

为验证算法准确性，首先与解析解对比。考虑无层间应力差情况，该情况下单裂缝扩展符合penny模型。矿场条件下，penny裂缝扩展主要为黏性主导能量耗散方式，因此采用黏性主导penny裂缝进行单缝验证。

单缝验证的基本参数为：排量 5 m3/min，流体黏度5 mPa·s，弹性模量30 GPa，泊松比0.2，断裂韧性0.2 MPa·m1/2，滤失系数0，注入时间10 min。径向裂缝扩展的特征时间为[30]：

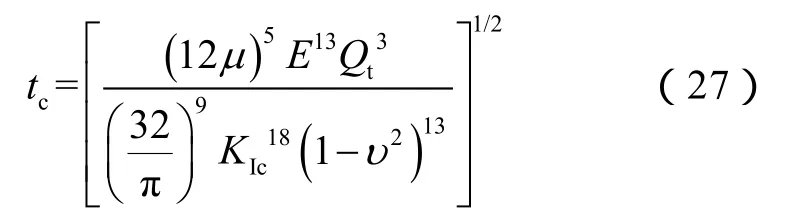
当注入时间远小于特征时间时，裂缝扩展能量消耗以缝内流动摩阻耗散为主；当注入时间远大于特征时间时，裂缝扩展能量消耗以尖端破裂能量耗散为主，两者中间为过渡过程。计算特征时间为3.30×109min，则注入时间（10 min）远小于特征时间，为黏性主导裂缝。黏性主导径向裂缝半径和裂缝入口宽度为[30]：

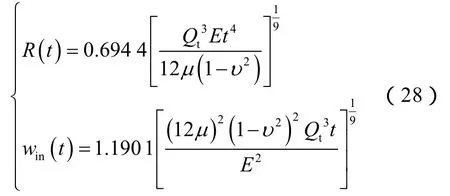
该算例采用单元尺寸为2.5 m×2.5 m，计算结果如图5所示。结果显示，本文算法计算结果与解析解吻合，表明算法可准确计算penny裂缝扩展动态。

3.1.2 与隐式水平集算法对比

为进一步验证算法准确性，考虑分层加载应力、流体发生滤失的情况，采用 Dontsov等[16]隐式水平集算法进行验证。设置3层最小主应力，如图6a所示。其他参数[16]为：弹性模量9.5 GPa，泊松比0.2，流体黏度 0.1 Pa·s，注入排量 0.01 m3/s，断裂韧性 1 MPa·m1/2，滤失系数 2.065×10-6m/s1/2。

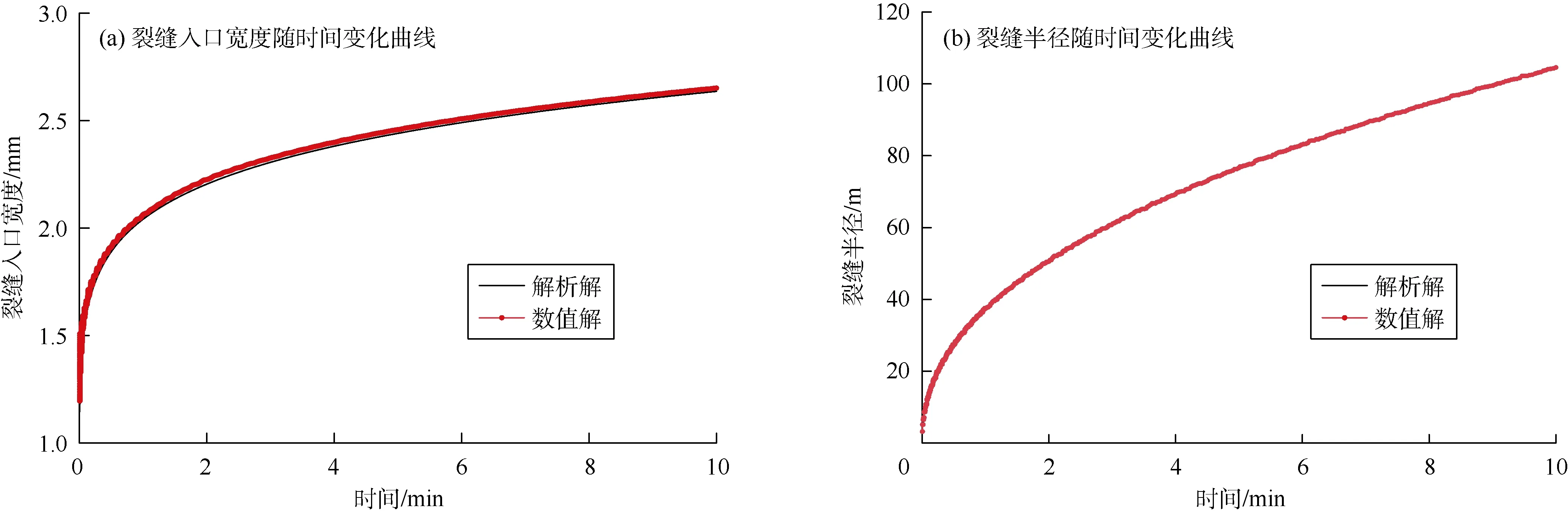
图5 本文算法计算结果与penny裂缝解析解对比

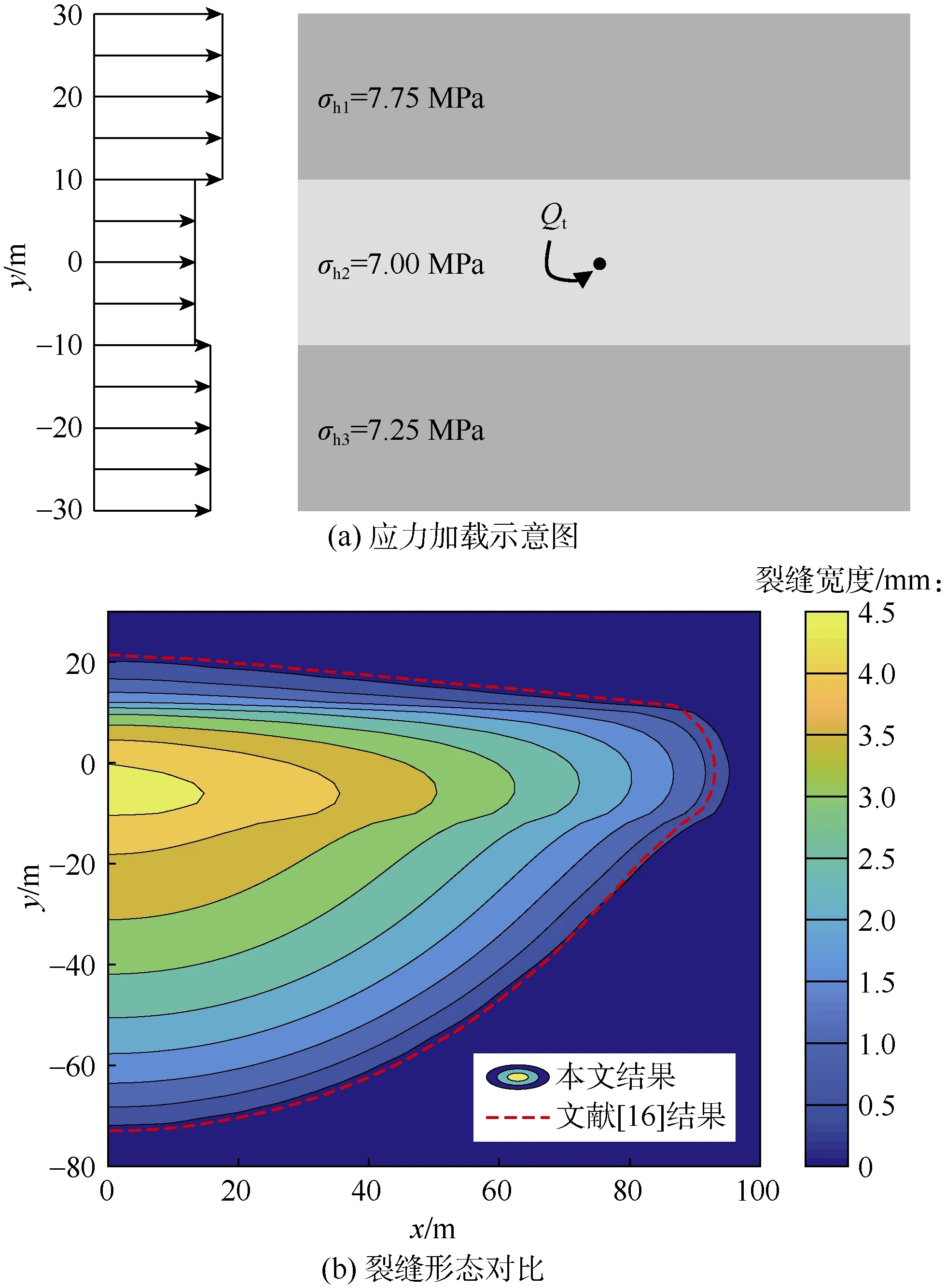
图6 分层加载应力、流体发生滤失情况下的裂缝扩展剖面与Dontsov等[16]隐式水平集算法裂缝扩展轮廓对比

图6b为注入3 600 s时本文算法得到的裂缝宽度剖面与文献[16]裂缝轮廓对比。结果显示，本文结果与Dontsov等[16]隐式水平集算法结果吻合，表明本文算法可以准确求解存在滤失的裂缝扩展形态。

3.2 计算效率对比

采用算例为澳大利亚国家科学院有机玻璃实验[27]。有机玻璃满足均质线弹性，并可以拍照监测裂缝扩展动态。具体实验参数为：流体黏度 30 Pa·s，有机玻璃弹性模量3.3 GPa，泊松比0.4。分3层加载水平应力，如图7所示。实验采用变排量注入[27]。图8为实验665 s时的裂缝形态与本文算法计算结果的对比。可以看出，本文算法计算结果接近实验获得的裂缝形态，进一步验证了本文算法准确性，也说明可以采用实验参数进行计算效率对比。

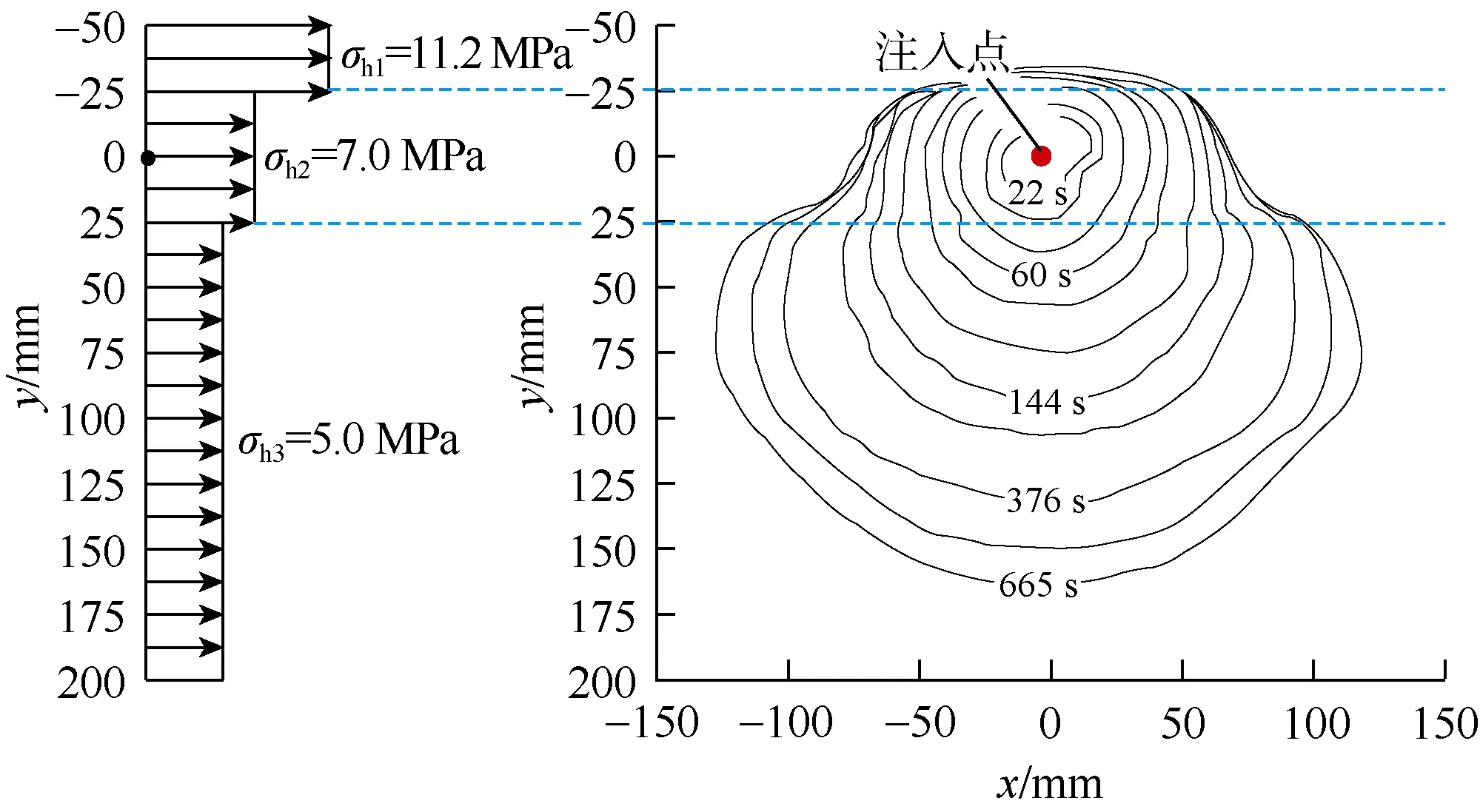
图7 Wu等[27]有机玻璃压裂实验应力加载与裂缝形态

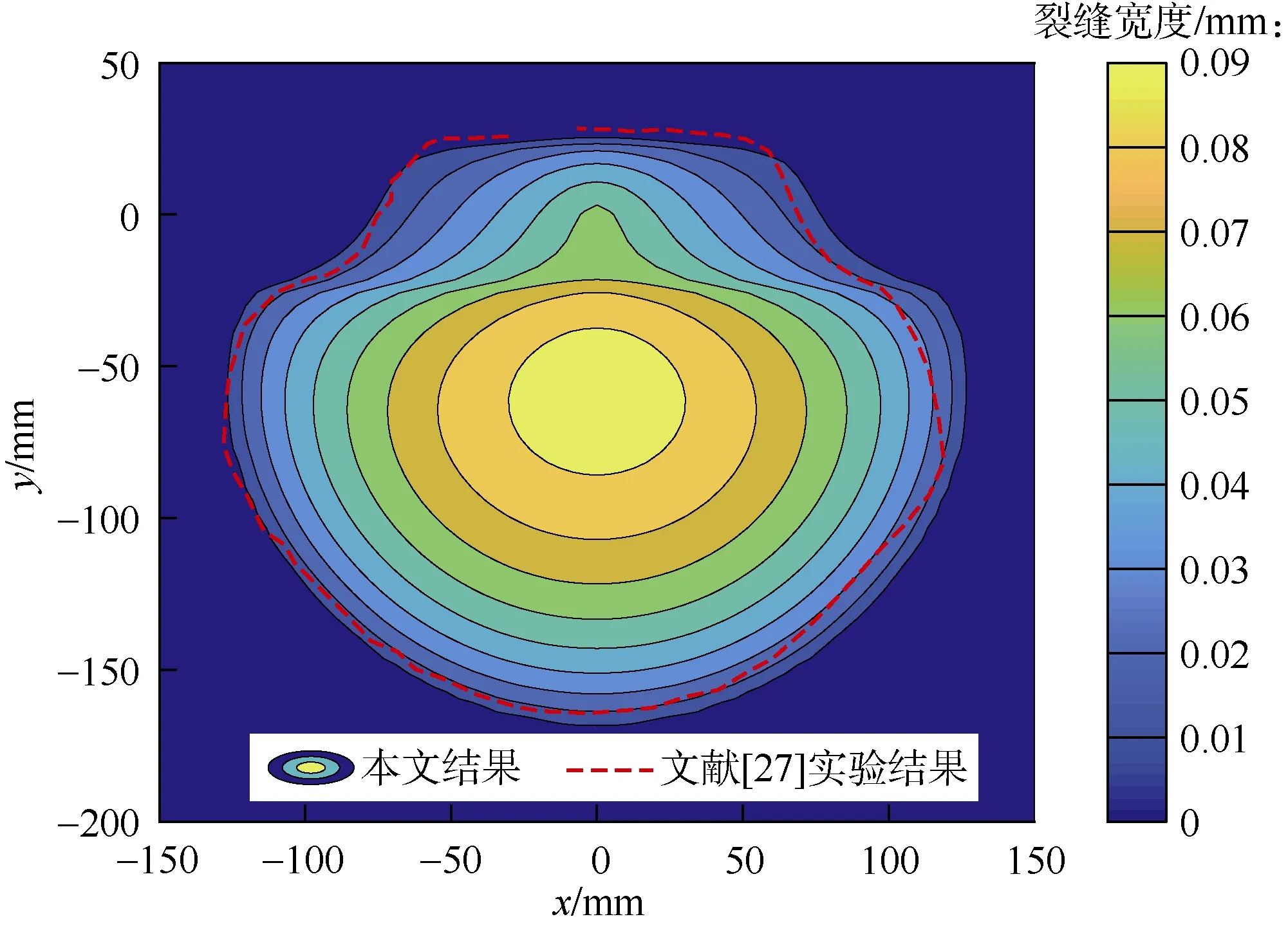
图8 本文算法与澳大利亚研究院实验结果对比

Zia等[28]采用隐式水平集算法及文献[27]中实验参数进行了计算，并评价了算法计算效率。本文采用与文献[28]相同大小网格（0.43 cm×0.43 cm），处理器均为Intel(R) Core(TM) i7-5600 CPU@2.60GHz。本文采用MATLAB编程，文献[28]采用Python编程，两种语言在科学计算方面执行效率相当，因此通过对比两者CPU占用时间确定本文算法与隐式水平集算法的计算效率。本文算法采用25、50与75级积分算法占用CPU时间均在300 s以内，其中75级积分算法占用CPU时间仅为73 s，而文献[28]隐式水平集算法占用CPU时间为619 s。可见本文算法计算效率大幅提高。

4 实际井算例分析

以浙江油田昭通页岩气示范区YS112H4水平井组YS112H4-1井为例进行实例分析。YS112H4-1井目的层为下志留统龙马溪组，采用小间距分段多簇压裂工艺，设计平均簇间距10 m，施工排量14 m3/min，施工液体为FAB-2滑溜水，密度为1 016 kg/m3，黏度为2 mPa·s。储集层厚度为34 m，水平应力差为17.0～19.5 MPa。岩石弹性模量为 35.7 GPa，泊松比为 0.27，断裂韧性为1.0 MPa·m1/2。储集层基质渗透率 1.0×10-7μm2，因此可以忽略流体向基质滤失。目标层段上下有一定应力遮挡，水平最小主应力剖面如图9所示。图9中z=0 m为射孔位置所在深度。孔眼直径12 mm，射孔修正系数0.7。

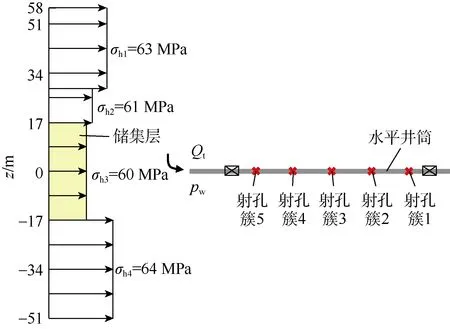
图9 地应力剖面与分簇射孔示意图

由于已有较多文献[38-40]分析分簇数、射孔直径等参数与各簇进液量的关系，本文重点分析实例井簇间应力分布、射孔数及射孔数分布等对各簇进液量和裂缝扩展的影响。

4.1 簇间应力分布对各簇进液的控制作用

4.1.1 簇间应力均质分布

首先分析地应力平面均质的情况，即各射孔簇最小水平主应力相同，均为60 MPa。该情况下射孔摩阻与缝间应力干扰控制各簇进液分布。

由图10可知，射孔簇应力均质分布情况下，每簇4、8、16孔的射孔方式各簇均能开启并进液。每簇4、8孔时，各簇进液量接近；每簇16孔时，外侧簇裂缝进液为中间簇裂缝进液的1.24倍。因此，单簇孔数越多，各簇进液量差异越大。

由图11可知，每簇4、8孔时，各簇裂缝长度接近；每簇16孔时，外侧簇裂缝半长为330 m，而中间簇裂缝半长为265 m，前者为后者的1.24倍，与进液量比例一致。由于产层上部应力小于产层下部应力，裂缝高度倾向于向产层上部扩展，而产层以下基本没有裂缝展布。中间簇近井区域裂缝高度大于外侧簇，说明近井区域的应力干扰最为显著，近井区域中间裂缝长度扩展受阻，因而容易发生纵向扩展。

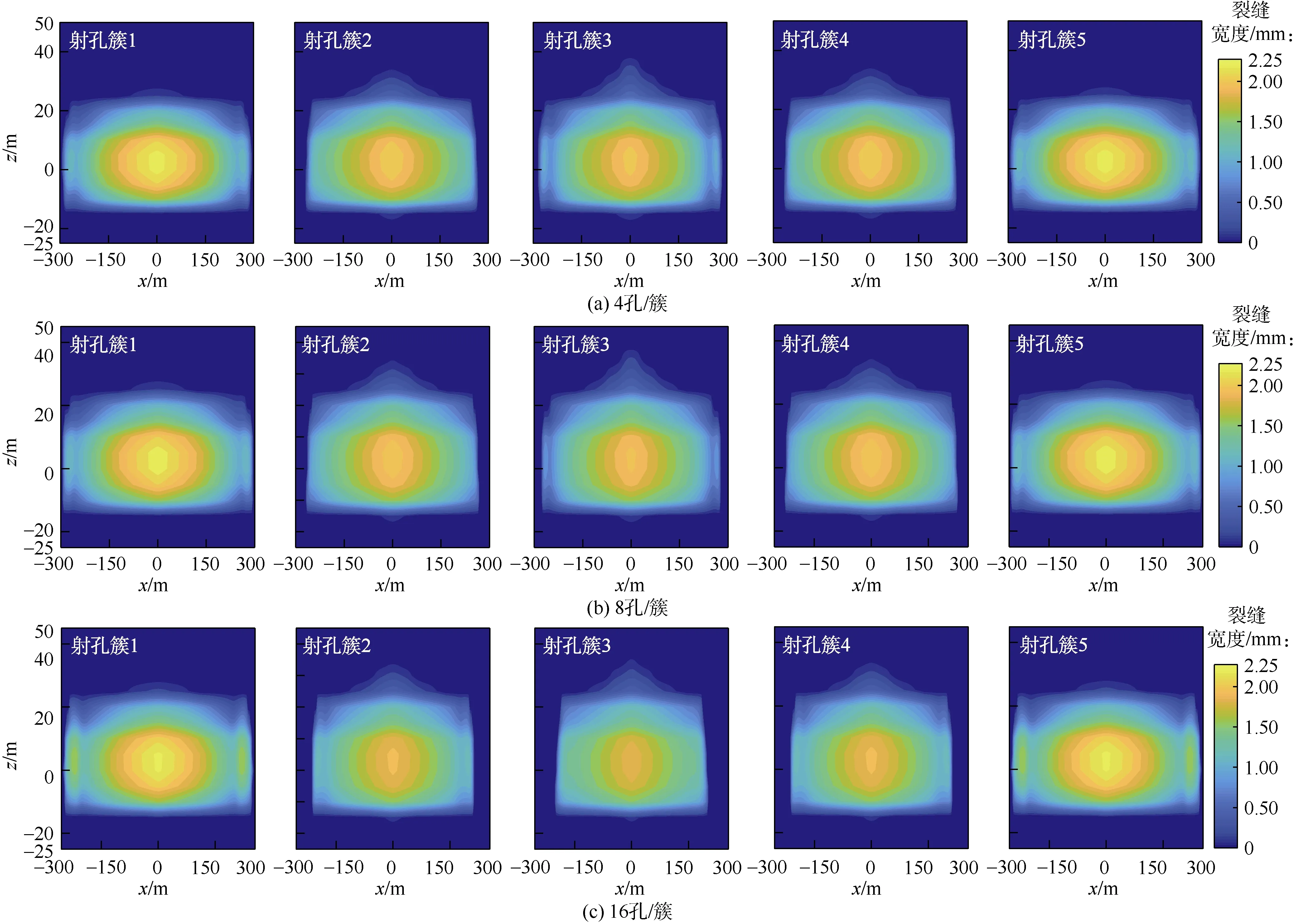
图11 簇间应力均质分布时的裂缝扩展形态

4.1.2 簇间应力非均质分布

设定射孔簇1—5所在层位的最小水平主应力分别为62，60，60，60，60 MPa，即射孔簇1最小水平主应力比其他射孔簇高2 MPa。

由图12可知，每簇4或8孔时，高应力簇进液量低于其他簇，但各簇均能进液；每簇16孔时，高应力簇不能开启进液。说明每簇16孔不能平衡簇间2 MPa应力差，每簇8孔可以实现各簇有效进液，每簇4孔各簇进液几乎没有差别。

结合簇间应力均质分布的进液情况可知，尽管射孔簇 1裂缝为应力干扰作用下的进液主导缝，但若其最小水平主应力高于其他簇 2 MPa，则可能无法开启进液。计算结果表明，簇间应力非均质对各簇进液的控制作用大于应力干扰。因此，簇间应力分布是分簇限流设计的重要参数。

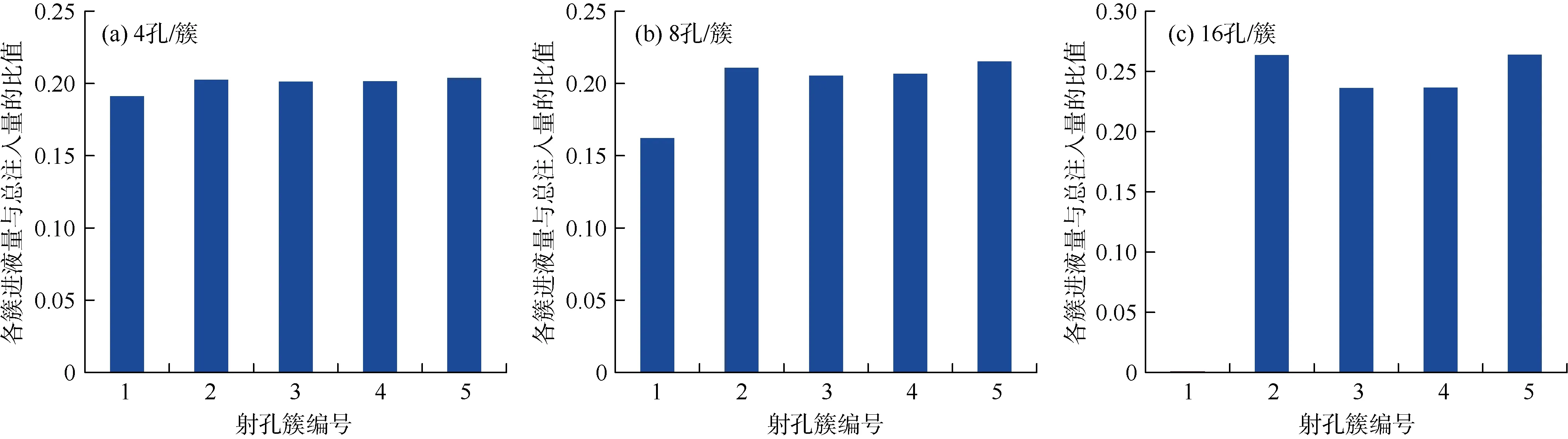
图12 簇间应力非均质分布时的各簇进液量分布

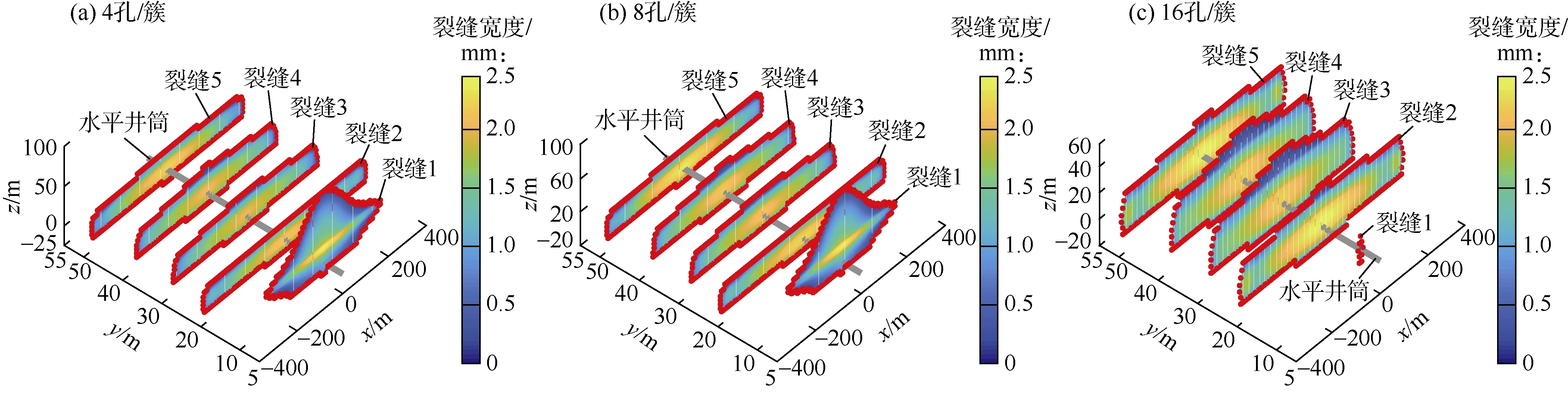
图13 簇间应力非均质分布时的裂缝扩展形态

由图13可知，每簇4、8孔时尽管各簇进液量差别不显著，但由于产层上部地应力小于产层下部地应力，同时裂缝 1长度扩展受到其他裂缝应力干扰“挤压”作用，因此裂缝 1倾向于向产层上部扩展，进而出现缝高过量扩展。裂缝扩展形态受层间应力剖面和应力干扰共同控制。水力裂缝会选择阻力最小路径扩展，当簇间应力干扰作用大于层间应力差作用时，裂缝会选择纵向扩展路径。受层间应力分布和应力干扰影响，高应力射孔簇的裂缝形态发生改变，进而影响改造效果。这表明各簇产量与进液量的关系不一定一致。这种现象也难以通过井下光纤温度或声监测识别，因此在设计阶段应对簇间应力分布进行细致解释分析，并尽量将应力接近的区域划分为一段。

4.2 射孔数分布对各簇进液的控制作用

4.2.1 簇间应力均质分布

Cramer等[41]通过现场试验井下拍照发现，由于射孔质量、射孔相位差别，压裂过程并非每个射孔均可开启，因此有必要分析不均匀射孔数对各簇进液的影响。设计 3种射孔方案进行对比：①各簇射孔数依次为8，9，8，8，8；②各簇射孔数依次为8，10，8，8，8；③各簇射孔数依次为8，11，8，8，8。设定各射孔簇最小水平主应力相同，均为60 MPa。

由图14可知，射孔簇2增加1～3孔之后，该簇进液最多。增加孔数越多，该簇进液量占比越大。增加1，2，3个孔时，射孔簇2进液量占总注入量的比例分别为21.5%，23.3%和25.0%。增加3个射孔后，射孔簇2与其他各簇进液量差异较大，因此应避免增加3个以上射孔数。由图15可知，某簇射孔数增加过多，会导致该簇裂缝缝长过大，簇间改造反而更不均衡。可见，增大某一簇的射孔数会提高该簇的进液量，从而平衡地应力、近井摩阻或应力干扰差异的影响，但射孔数增加不应过多，增加1～2孔的作用已经非常显著。本文模拟结果与Cramer等[41]现场试验得到的认识一致。

图14 簇间应力均质分布时不同射孔方案的各簇进液分布

4.2.2 簇间应力非均质分布

设定射孔簇1—5所在层位的最小水平主应力分别为62，60，60，60，60 MPa，即射孔簇1最小水平主应力比其他射孔簇高2 MPa。为增加射孔簇1的进液比例，设计3种射孔方案：①各簇射孔数依次为9，8，8，8，8；②各簇射孔数依次为10，8，8，8，8；③各簇射孔数依次为11，8，8，8，8。

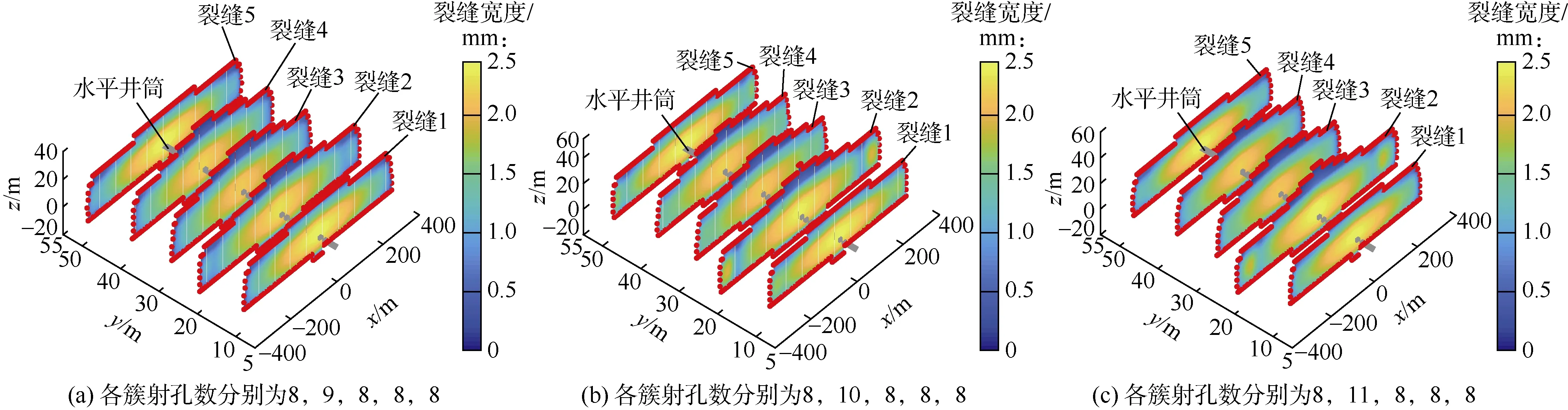
图15 簇间应力均质分布时不同射孔方案的裂缝扩展形态

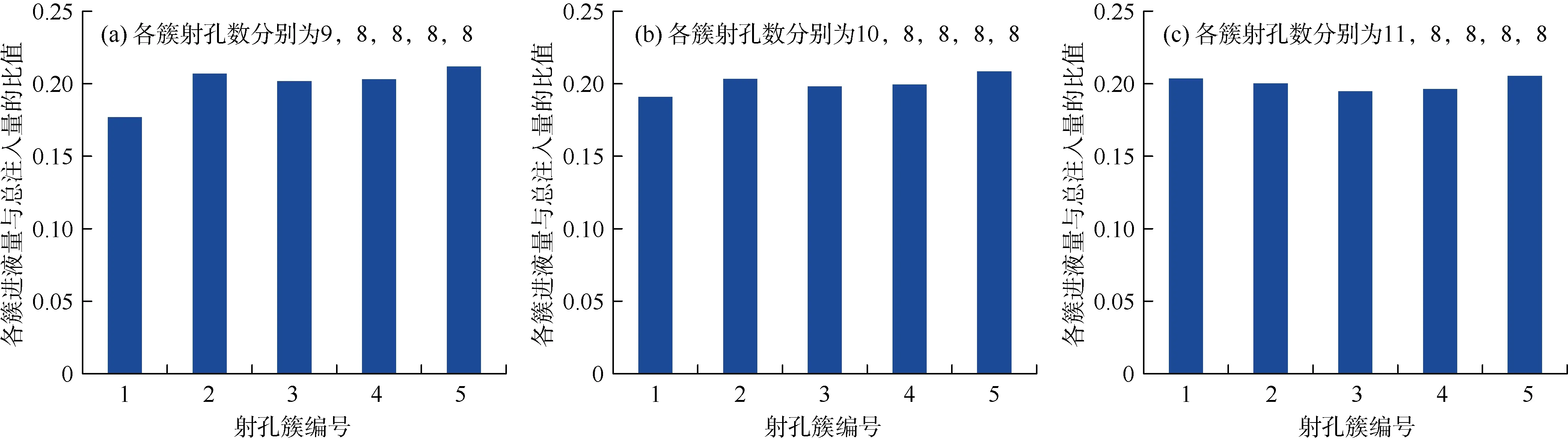
图16 簇间应力非均质分布时不同射孔方案的各簇进液分布

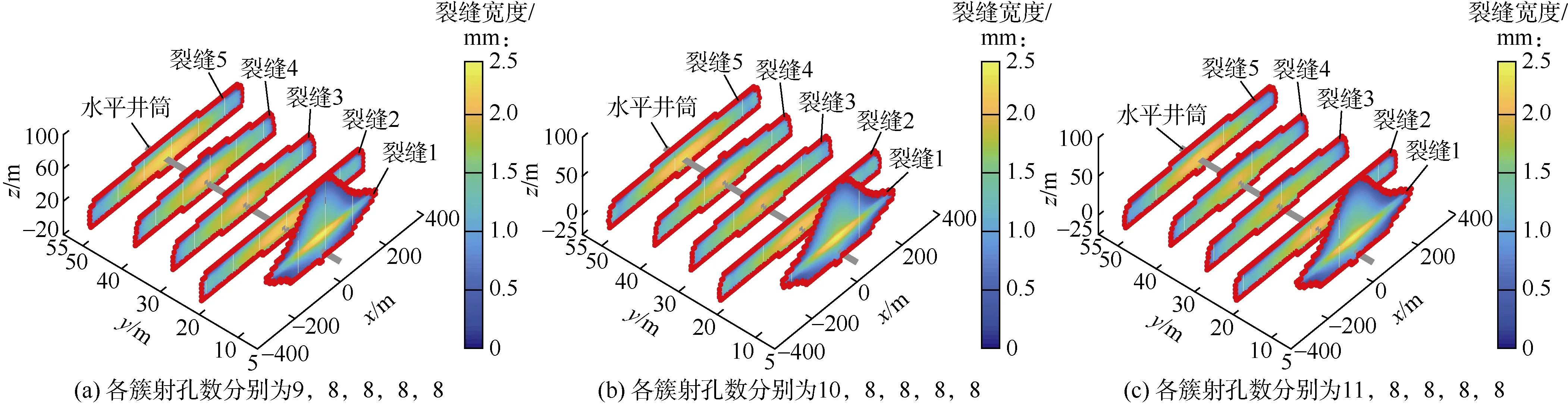
图17 簇间应力非均质分布时不同射孔方案的裂缝扩展形态

由图16可知，尽管射孔簇1为高应力簇，但增加该簇1～3个射孔后，该簇进液量与其他4簇差异逐渐减小，增加该簇 2个射孔即可实现均匀进液。但从图17可以看出分析，高应力簇的改造仍然不充分，裂缝1缝高出现过量扩展。由于裂缝1在产层内扩展受到其他簇较大应力干扰作用，水力裂缝会沿最小阻力路径扩展，因此裂缝1倾向于向产层上部扩展，导致裂缝1缝高扩展过大，产层改造面积不足。同时，增加 3孔与增加 2孔的裂缝形态较为接近。研究表明，增加高应力簇2个射孔数可以提高该簇进液，达到均匀进液；均匀进液并不意味着裂缝形态均匀，裂缝形态受应力干扰和层间应力剖面两方面控制。体积改造多簇压裂设计应加强对层间应力剖面、层内平面应力分布的解释，并应尽量将应力接近的地层作为一段进行分簇压裂。

5 结论

提出了水平井分段压裂平面三维多裂缝扩展模型求解新算法，算法准确可靠，与目前广受认可的隐式水平集算法相比，新算法计算速度大幅提高。以浙江油田昭通页岩气示范区下志留统龙马溪组页岩气水平井实际参数进行模拟分析，研究发现：各簇射孔数相同时，簇间应力非均质对各簇进液的控制作用大于应力干扰，减小单簇射孔数可以平衡簇间应力差异，实现均衡进液；调整各簇射孔数量可以实现均衡进液，各簇射孔数差别应控制为1～2孔，簇间射孔数差别太大，会引起液体过多进入射孔数最多的簇，反而加重各簇进液不均匀，不利于各簇均衡改造；增加高应力簇的射孔数有利于均匀进液，但进液均匀并不等于裂缝形态一致，裂缝形态受应力干扰和层间应力剖面共同控制；水力裂缝沿最小阻力路径扩展，对于高应力射孔簇，若层间应力差较小，高应力簇裂缝更容易沿纵向扩展，不利于产层内储集层改造，体积改造应选择应力接近的区域作为一段。

致谢：感谢国家留学基金委的资助，感谢中国石油勘探开发研究院王臻博士在算法设计方面给予的帮助。

符号注释：

A——裂缝覆盖区域面积，m2；A——流动方程系数矩阵；A(t)——t时刻的裂缝覆盖区域面积，m2；Cg——边界积分方程格林函数，具体形式可参见文献[34]，Pa/m3；C——影响系数矩阵，Pa/m；Clv——滤失系数，m/s1/2；dk——第k簇裂缝的射孔直径，m；E——岩石弹性模量，Pa；G——剪切模量，Pa；h，r——网格单元在z方向的序号；i，m——网格单元在x方向的序号；i0，j0，h0——注入点单元在x，y，z方向的序号；j，n——网格单元在y方向的序号；k——裂缝簇序号；K——射孔磨蚀修正系数；KIc——Ⅰ（张）型裂缝断裂韧性，Pa·m1/2；M(w)——（17）式等号右端项对应的系数矩阵；nf——每段簇数；nk——第k簇裂缝的射孔数；p——缝内流体压力，Pa；p——缝内流体压力矩阵，Pa；p0——初始时刻的缝内流体压力，Pa；p0——初始时刻的缝内流体压力矩阵，Pa；pin,k——第k簇裂缝的裂缝入口压力，Pa；pp,k——第k簇裂缝的射孔摩阻，Pa；pα——tα时刻的缝内流体压力，Pa；pw——井底压力，Pa；q——单位长度体积流量矢量，m2/s；Qk——第k簇裂缝的进液流量，m3/s；Qt——注入排量，m3/s；R——裂缝半径，m；s——距缝尖的距离，m；S——源汇项系数矩阵；t——时间，s；t0(x,y,z) ——坐标(x,y,z)处发生滤失的时刻，s；t0a，t0b，t0c，t0d，t0e——a、b、c、d和e单元开启时间，s；tc——径向裂缝扩展的特征时间，s；tf——注入时间，s；tα——第α时间步，s；Δt——时间步长，s；ΔtE——显式欧拉差分格式时间步长，s；v——裂缝尖端扩展速度，m/s；vba，vca，vda，vea——b、c、d和e单元到a单元的扩展速度，m/s；w——裂缝宽度，m；w——裂缝宽度矩阵，m；w0——初始时刻的裂缝宽度；w0——初始时刻的裂缝宽度矩阵；win——裂缝入口宽度，m；wα——tα时刻的裂缝宽度，m；wα——tα时刻的裂缝宽度矩阵，m；——裂缝平均宽度，m；x，y，z——场点坐标，m；x'，y'，z'——源点坐标，m；Δx，Δy——空间步长，m；α——时间步编号；δ——常量，无因次；δk(x,y,z)——第k簇裂缝的狄拉克函数，m-2；θ——常系数，0≤θ≤1；μ——流体黏度，Pa·s；ρ——液体密度，kg/m3；σh——最小水平主应力，Pa；σh——最小水平主应力矩阵，Pa；Δτ——RKL方法的时间步长，s；υ——岩石泊松比。