大跨悬浇钢筋混凝土拱桥施工扣索力优化计算分析*

刘增武 周建庭 吴月星

(重庆交通大学土木工程学院 重庆 400074)

近年来国内采用悬臂浇筑法相继建成了四川白沙沟1号桥[1-2]、四川新密地大桥[3-5]、四川鳡鱼大桥、贵州木蓬大桥[6]、贵州马蹄河大桥[7]、贵州夜郎湖大桥[8-9]、重庆武隆龙溪乌江大桥、重庆涪陵乌江大桥复线桥和贵州沿河沙坨大桥及在建的四川鸡鸣三省大桥等10座混凝土拱桥。与混凝土斜拉桥悬臂浇筑施工相比，钢筋混凝土拱桥悬臂浇筑施工过程中，扣索力的大小对拱圈结构的内力和线形的影响十分显著。由于拱圈内未布设预应力，其敏感程度远远大于斜拉桥，索力调整稍有不慎，就会导致拱圈开裂，这是钢筋混凝土拱桥悬臂浇注施工控制中的一个难点。

目前，已有学者在扣索力计算方面做了大量研究[10-14]，但对悬臂浇筑扣索力控制算法研究甚少，李晓斌[15]采用应力平衡法来求解白沙沟大桥扣索力并通过缩尺模型进行验证；张万晓[16]针对“应力平衡法”的不足，提出了“带有预判机制的扣索力可行域计算法”，但公式复杂、计算量较大。

鉴于此，本文以国内某大跨悬浇单箱室钢筋混凝土拱桥为依托，基于未知荷载系数法，结合优化理论与影响线原理，开展拱圈施工全过程扣索力优化计算分析，控制拱圈悬浇施工中内力与线形，避免反复调整扣索力，降低施工风险。

1 扣索力优化算法原理及步骤

扣索力优化计算分4步进行，计算分析过程中涉及到未知荷载系数法、优化理论、影响线及无应力状态合龙等相关原理。

1.1 未知荷载系数法

结构分析是在已知荷载条件下求解结构的位移、内力等结果，但是在大跨结构的设计中经常会遇到求满足某种已知条件的荷载的问题。midas Civil通过设置限制条件并定义目标函数使用优化方法计算此类问题，其中限制条件可以输入平衡条件也可以输入不平衡条件。满足指定的弯矩分布或指定的位移条件的顶力计算示意见图1，求解要点如下。

1) 将每个要计算的荷载定义为1个荷载工况，力的大小为单位力。

2) 使用已知荷载条件(均布荷载)和定义的单位力进行结构分析。

3) 使用限制条件建立如下平衡条件。

式中：MAi为在i处作用单位力时A点弯矩(i=1,2)；MBi为在i处作用单位力时B点弯矩(i=1,2)；MAD为其他荷载作用下的A点弯矩；MBD为其他荷载作用下的B点弯矩；MA为其它荷载和未知荷载共同作用下A点弯矩；MB为其他荷载和未知荷载共同作用下B点弯矩；P1，P2为未知荷载重量。

4) 因为未知荷载的数量和方程数量相同，所以直接解方程组即可获得所需解。

图1 未知荷载系数法示意图

通过设置合理的位移约束条件，利用未知荷载系数法求取拱圈最大悬臂状态下的初始扣索力，使得成拱线形逼近拱圈一次落架线形。

1.2 优化理论

1.2.1拱桥悬浇施工中受力特点

1) 拱圈在悬臂浇筑过程中的受力状态与悬臂曲梁类似，拱圈的上下缘反复出现拉压应力。

2) 拱圈在合龙前对扣索力非常敏感，索力稍有不妥便会导致拱圈产生过大拉应力。

1.2.2扣索力优化数学模型构建

利用未知荷载系数法获取扣索力初值后，通过建立拱桥悬浇施工逆过程模型，提取桁架单元内力，再进行拱桥悬浇施工正装分析。基于拱桥悬浇施工中的力学原理，通过获取正装施工过程中应力、位移，以及索力影响矩阵，并结合优化理论和自编的MATLAB优化程序对扣索力进行优化，主要过程如下。

1) 获取影响矩阵。

在施工阶段正装分析模型中，不计拱圈及扣索自重，依次对1～n号扣索施加单位力，计算由n组单位索力产生的拱圈截面应力、位移响应值，分别提取各控制截面的上、下缘应力aij、bij及位移vij，将其依次投放到影响矩阵A、B及V相应的位置，形成扣索张拉对拱圈截面上、下缘应力的影响矩阵A、B和位移影响矩阵V。

式中：aij、bij和vij分别为第j号扣索张拉单位力时，在第i个控制截面的上、下缘产生的应力及第i个控制截面的位移，i,j=1,2,…,n。

在张拉第n号扣索力时，已张拉的第1～(n-1)号扣索力亦将发生改变，因此索力向量I应计入该影响，记该影响矩阵为C。在张拉第j号扣索，对其本身的影响为1，对尚未张拉的扣索影响为0，即影响矩阵C中主对角线以下部分元素都为0，ΔCij为张拉第j号扣索单位索力对i号扣索的影响值，i≤j。

于是得到考虑扣索之间的相互影响的上缘应力的影响矩阵D、下缘应力的影响矩阵E及位移影响矩阵F。

式中：D=AC；E=BC；F=VC；dij、eij、fij分别为考虑扣索之间的相互影响第j号扣索张拉单位索力时，在第i个控制截面产生的上、下缘应力及位移。

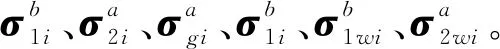
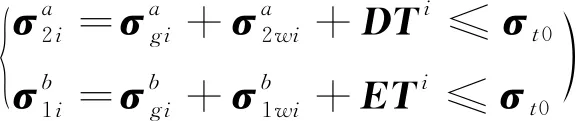
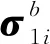
2) MATLAB优化计算。以拱圈各控制断面位移与拱圈各测点目标位移差的平方和为目标函数的数学模型如下。

设计变量：Ti∈TN,i=1,2,…,n。

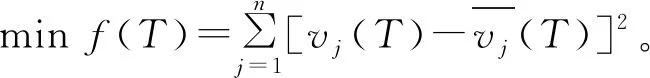
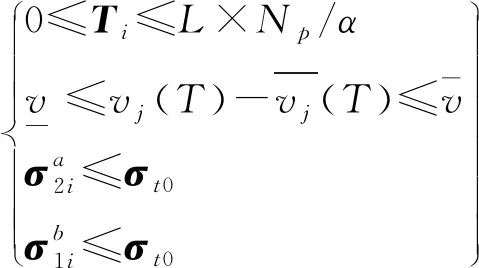
优化模型为典型的二次规划模型，考虑到计算规模较大，自编程序收敛性较差，使用MATLAB中自带的“quadprog”函数，可快速稳定地获取最优解。

1.3 扣索拆除、补张拉原则

1.3.1基于影响线的扣索拆除原理

大跨钢筋混凝土拱桥在悬浇过程中，随着悬臂段长度的增加，扣索力急剧增大可能导致拱圈部分截面拉应力超限，此时若拆除部分扣索可有效地改善拱圈受力状态，使截面应力处于容许范围内。在扣索力计算时当拱圈悬臂端出现下挠时(见图2),意味着增大扣索的索力值对改善拱圈悬臂端部的线形效果有限，容易导致扣索n的安全系数低于2.5，增大悬浇施工风险。相反，基于拱圈悬臂端部挠度影响线可知，可通过拆除扣索m，即相当于在拱圈顶部施加了一个斜向下的作用力F(见图3),使得拱圈悬臂端部向上变形，以改善拱圈的悬臂端部线形与受力状态。

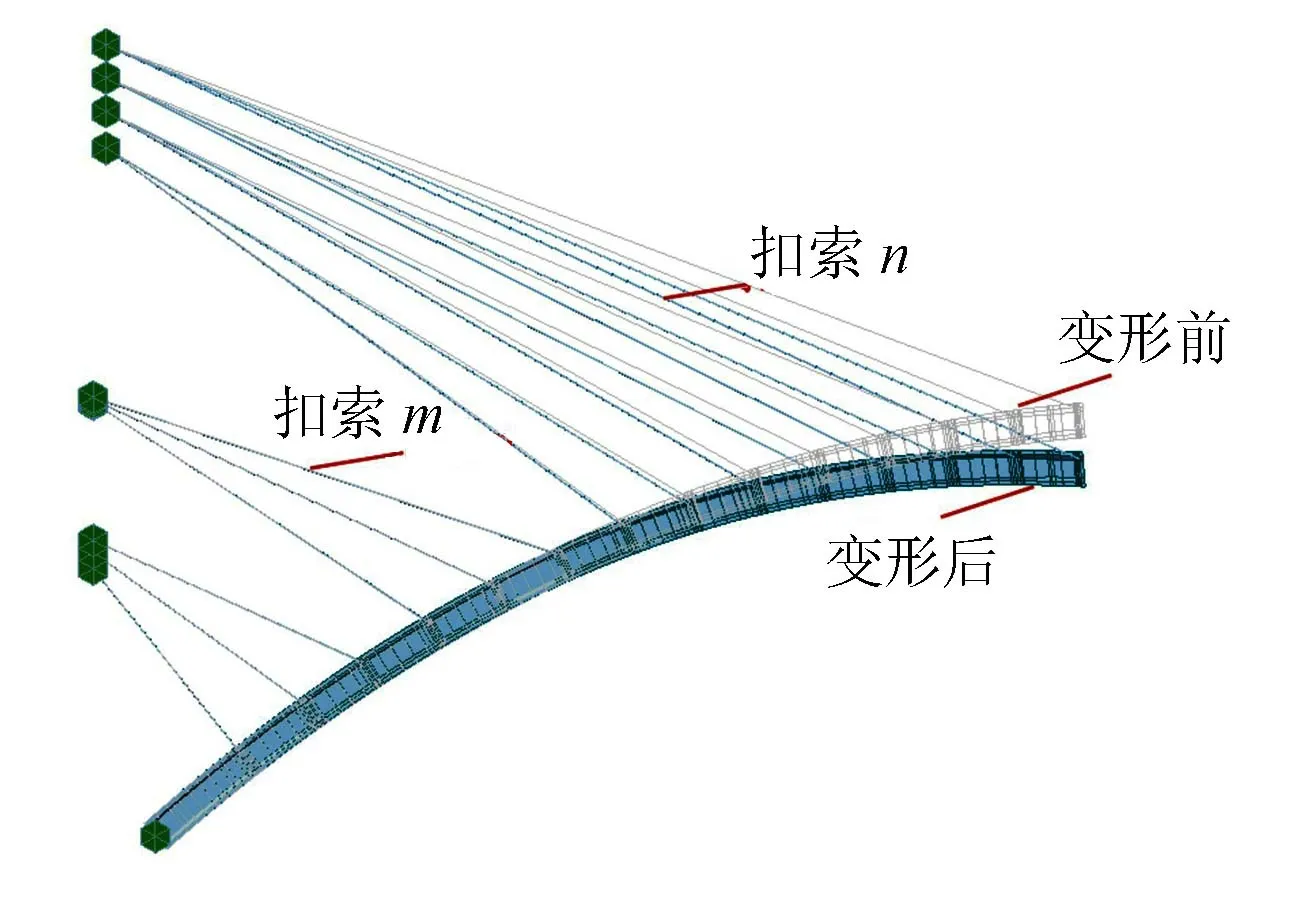
图2 悬臂端下挠示意图

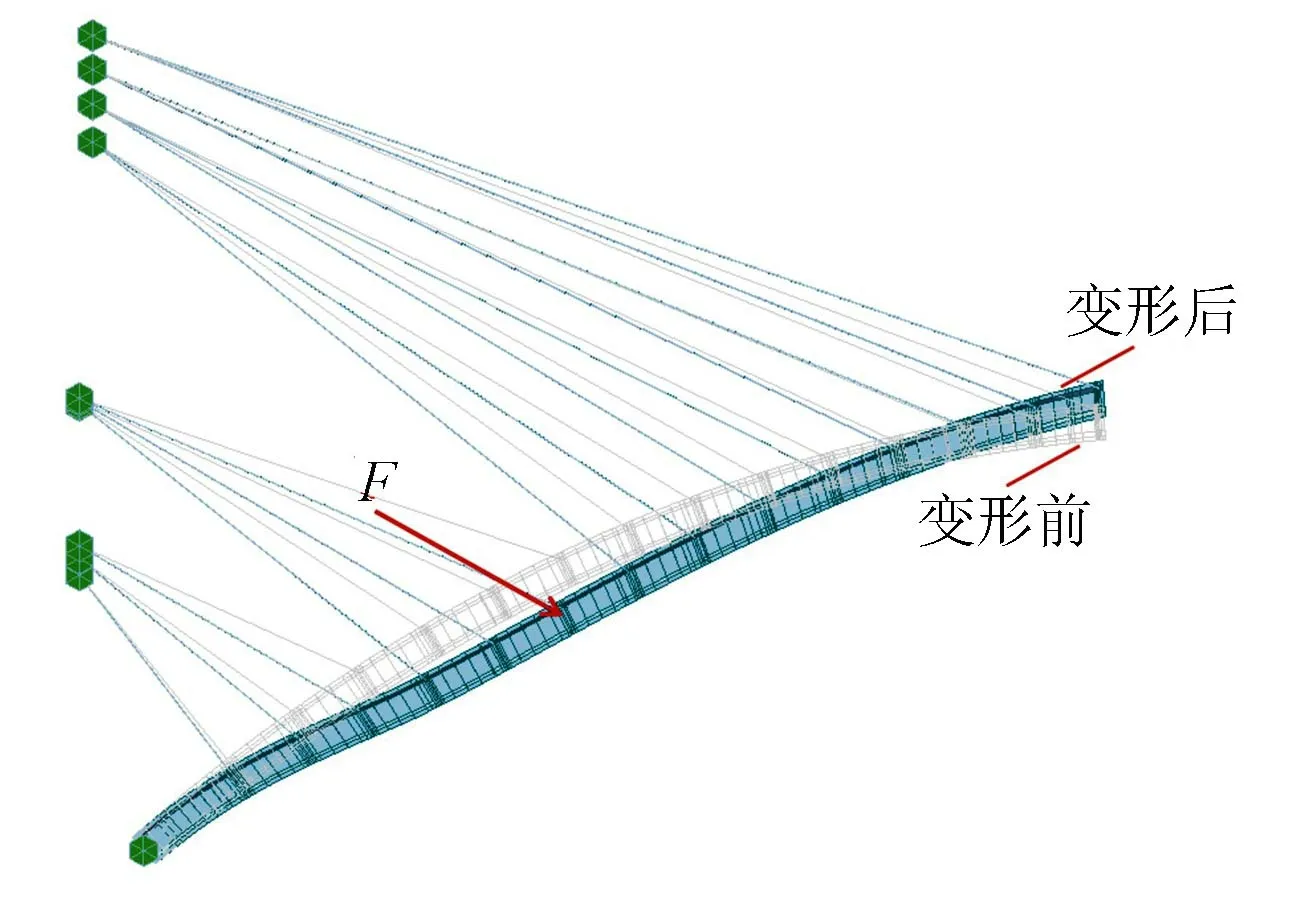
图3 基于影响线的扣索拆除示意图

1.3.2基于无应力状态法的扣索补张拉原理

当主拱圈处于最大悬臂状态时，在确保拱圈不出现拉应力超限的前提下，可通过调整索力使拱圈合龙段以无应力状态安装。为此，在实际扣索力优化计算时，可通过对扣索进行补张拉或松索使得主拱最大悬臂端的纵向位置和水平倾角必须尽可能接近无应力状态(DX≈0，Ry≈0)，以保证合龙段以制作线形安装。拱圈合龙段无应力安装示意图见图4。

图4 拱圈合龙段无应力安装示意图

1.4 扣索力优化计算步骤

扣索力优化计算分析流程见图5。

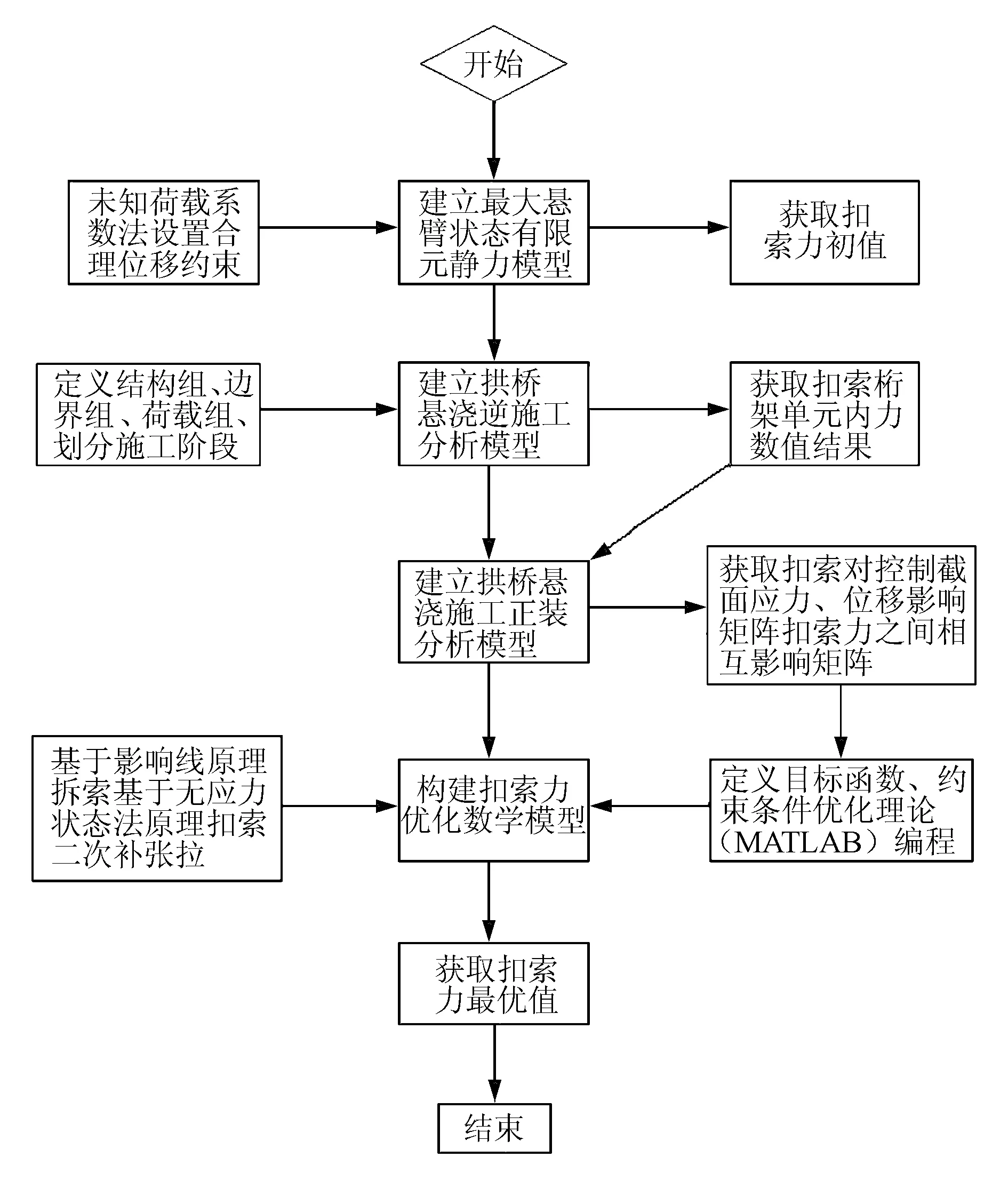
图5 拱圈悬浇施工扣索力优化流程图

2 算例验证

2.1 算例工程概况

算例为某大跨悬浇钢筋混凝土拱桥，净跨径为210 m，净矢跨比为1/5，拱轴系数m=1.67，拱圈悬浇施工示意见图6。拱圈为箱型截面，宽7.0 m、高3.5 m，顶、底板厚度由80 cm渐变至40 cm，腹板厚度由80 cm渐变至50 cm，其他节段顶、底板厚40 cm，腹板厚50 cm。

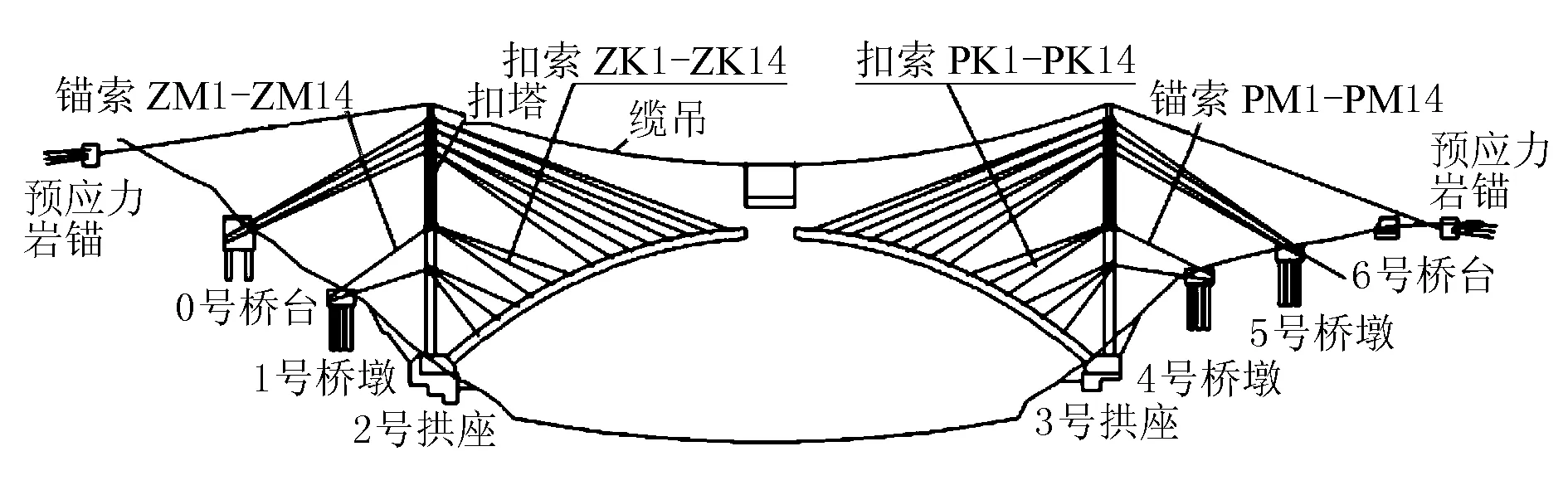
图6 拱圈悬浇施工示意图

2.2 有限元建模

拱圈采用梁单元模拟，扣索采用桁架单元模拟；拱脚采用一般支承模拟，约束所有自由度；拱脚支架现浇段采用只受压弹性支承模拟；扣索与拱圈采用弹性连接中的刚性连接模拟；拱圈横隔板采用集中荷载进行模拟；拱圈节段混凝土湿重、挂篮荷载以集中力的方式模拟。有限元模型见图7。

图7 大桥有限元模型

2.3 扣索力优化计算结果

基于扣索力优化计算结果，最终施工阶段划分表见表1。

表1 施工阶段划分表

续表1

由表1可知，拱圈8号节段、10号节段、12号节段及14号节段浇筑完成后，需要拆除2号、3号、4号及5号扣索；在张拉完成14号扣索后，为改善拱圈受力状态，需拆除5号扣索；计算分析发现，拆除5号扣索必须在张拉完14号扣索之后，两者施工顺序不能相反，否则拱圈拉应力超限；施工阶段51至53，分别对14号、12号、11号扣索索进行补张拉，改善拱圈最大悬臂状态下拱圈受力状态；拱圈合龙后，从拱顶向拱脚方向依次拆除剩余扣索。

扣索力优化计算后，重新做施工阶段正装分析，获取拱圈松索成拱后线形结果。扣索初张拉值与拱圈各节段悬臂端点下挠图分别见图8、图9。

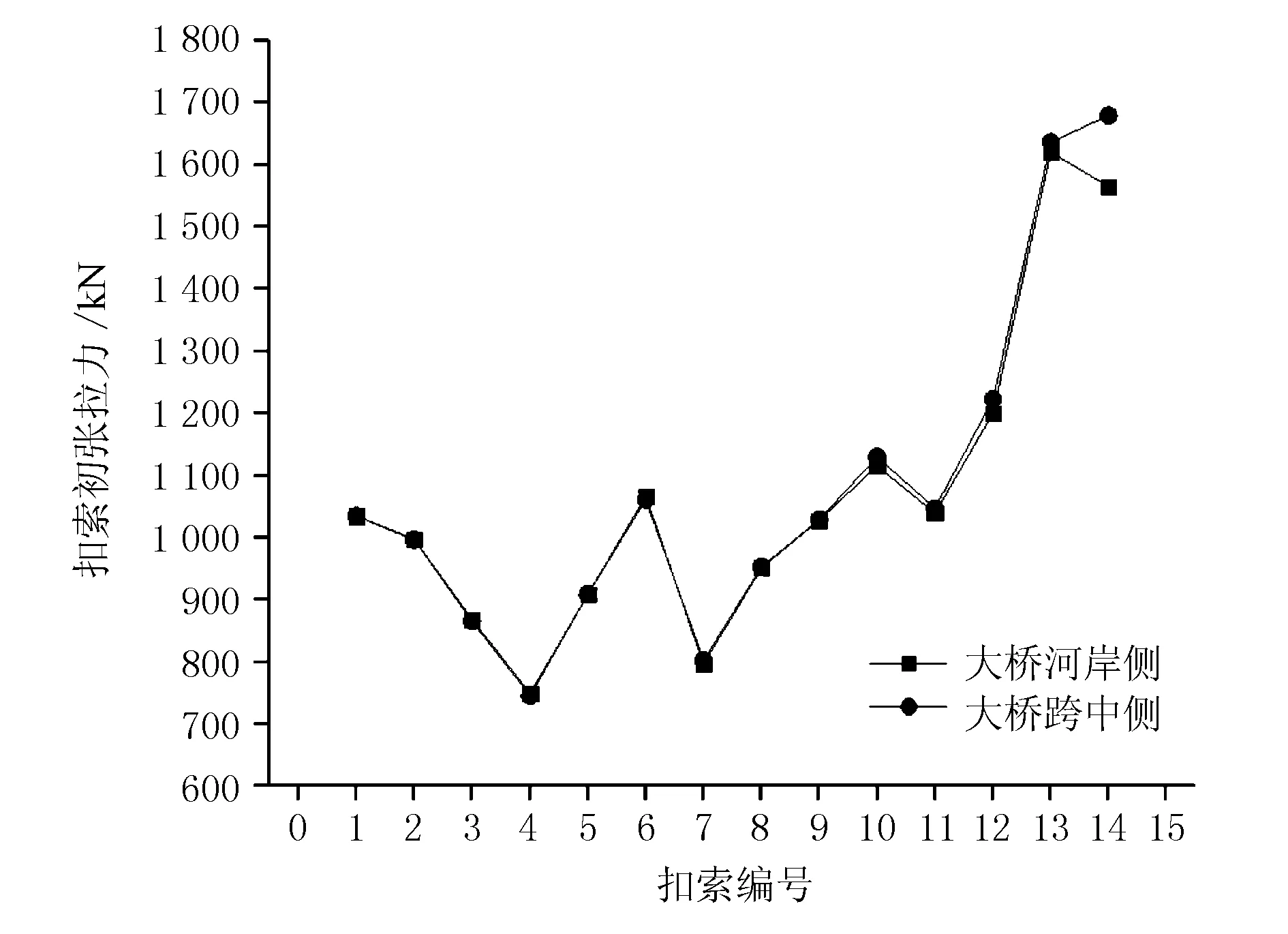
图8 大桥各扣索初始张拉力

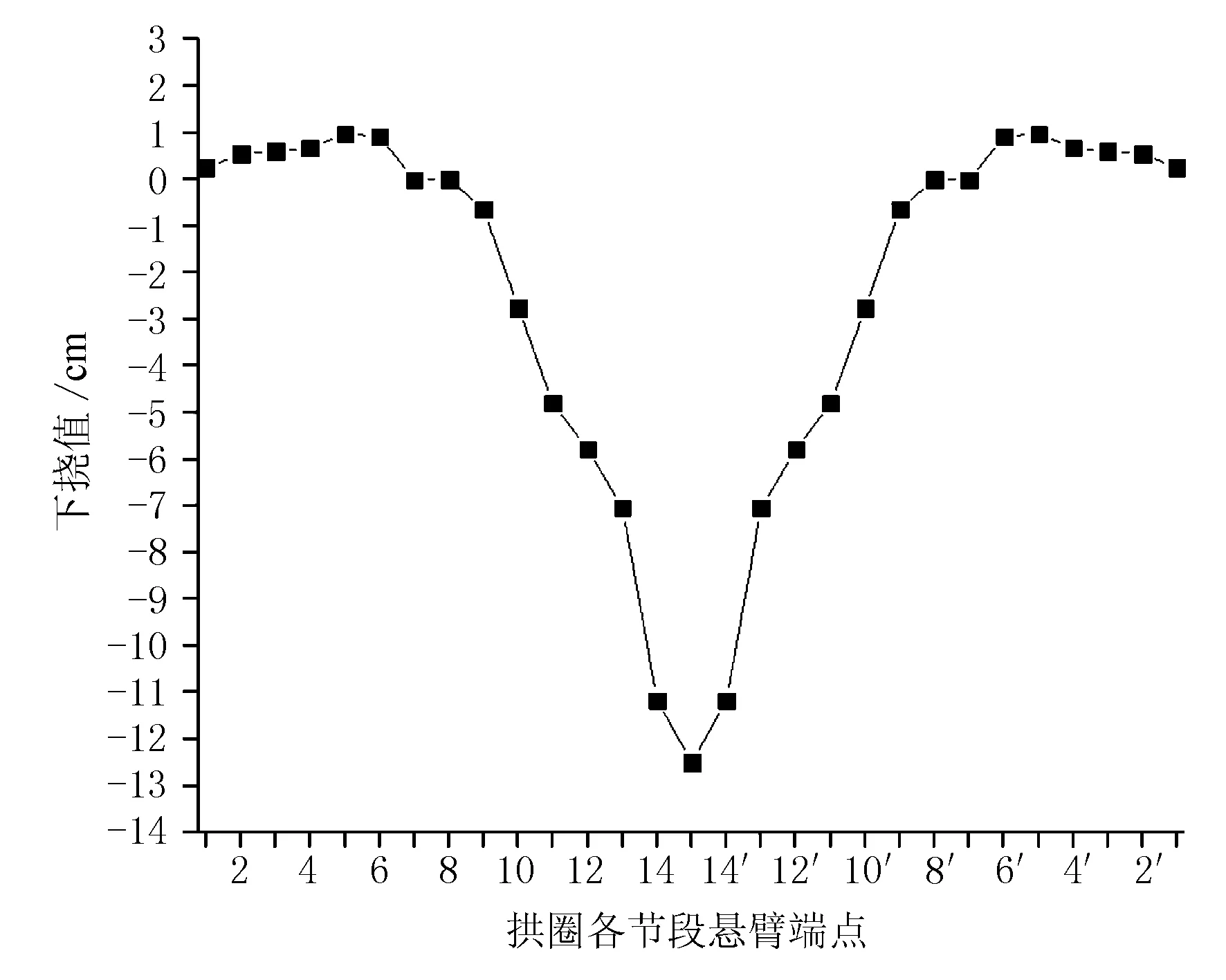
图9 拱圈各节段悬臂端点下挠图

由图8、图9可知，1号～14号扣索初始张拉力分布较为均匀，总体上，随着扣索长度增加，扣索水平倾角减小，扣索力逐渐增大，但所有扣索力安全系数均大于2.5，安全储备较高。拱圈松索成拱后各节段悬臂端点位置挠度从拱脚位置向拱顶位置依次增大，松索成拱后拱圈线形良好，未出现“马鞍形”。

获取两典型工况下拱圈10号扣锚索张拉工况和拱圈11号节段浇筑工况拱圈应力云图，见图10、图11。

图10 拱圈10号扣锚索张拉工况下拱圈应力值

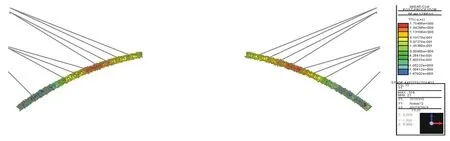
图11 拱圈11号节段浇筑工况下拱圈应力值

由图10、图11可知，拱圈受力状态基本与本文1.2.1节中总结的规律相符，悬臂浇筑拱圈节段混凝土时，已浇筑完成的拱圈截面上缘会产生拉应力，下缘产生压应力；张拉扣索后拱圈截面上缘产生压应力，下缘产生拉应力，拱圈截面在整个悬臂浇筑过程中会反复承受2种受力状态的变化直至合龙。张拉10号扣锚索时，拱圈下缘产生的最大拉应力为0.6 MPa，而浇筑拱圈11号节段混凝土时，在拱圈上缘产生约1.8 MPa拉应力，但均小于设计容许拉应力值，拱圈施工全过程受力合理，不会出现开裂现象。

3 结语

1) 在悬臂浇筑过程中扣索力较为均匀、拱圈最大拉应力为1.8 MPa，且松索成拱线形合理，未出现“马鞍形”，表明本文算法可靠。

2) 结合影响线原理和无应力状态法原理，可对扣索最优拆除顺序与补张拉力进行判断分析。

3) 采用未知荷载系数法可快速对拱圈最大悬臂内力状态进行调整，改善成拱后拱圈的受力状态。