不同悬沙组分对潮流的响应关系研究

朱子晨胡泽建刘建强张莞君张永强黄炳智

(自然资源部 第一海洋研究所,山东 青岛266061)

海湾是海洋资源开发利用的重要区域,由于其优良的自然环境和开发条件,海湾地区往往是人口聚集、经济发展的中心区域[1]。对多数海湾地区而言,由于具有较好的波浪掩护条件,潮流常常是泥沙运动的主要动力因素。而海湾内的泥沙运动,影响着地形地貌及湾内港口、能源工程的运营和维护[2-3]。悬浮泥沙能够吸附重金属等化学物质,对光具有吸收作用,又对海湾的生态环境具有显著影响[4]。海水中的悬浮泥沙来源于再悬浮、水平输运等方式,其组成中包含多种粒径成分。由于不同粒径的泥沙,其起动、沉降等特征均不相同,各成分的百分含量在一个潮周期内具有较为明显的变化。王爱军等[5]2005年对长江口悬沙粒度与浓度关系的研究显示,特征时段内悬沙中值粒径与浓度存在指数关系；张一乙等[6]2016年对长江口悬沙组分对再悬浮过程响应的研究显示,砂质组分是悬沙中对再悬浮过程响应的敏感组分；陈语等[7]2016年对长江口浑浊带悬沙粒度分布的研究显示,悬沙粒度的垂向差异在大潮期十分显著,而小潮期粒径垂向梯度较低；徐海和李伯根[8]2009年对椒江河口悬沙分选机制研究的结果表明,悬沙粒径分选主要受物质来源、潮流动力作用下底质再悬浮、絮凝沉降三个因素影响。这些研究表明,我国河口、海岸带地区悬沙组成的变化规律受到广泛关注。泥沙组分的运动、变化规律与海洋开发及环境保护息息相关,如某些海域开发后,人工构筑物附近出现的泥化现象等。为探究潮流作用下悬浮泥沙组成成分对动力因素的响应机制,本文采用观测与模型相结合的方法,选择潮差较大、波浪掩护条件较好的湄洲湾罗屿支水道为目标区域,对半日潮周期的时间尺度内悬沙组成的变化特征进行探讨。

1 研究方法

1.1 水动力观测与泥沙取样分析

湄洲湾位于福建省莆田、泉州两市之间,秀屿站1978-01—1980-12潮汐观测显示,该地区平均潮差5.12 m,最大潮差7.59 m,潮差较大,且海湾狭长,波浪掩护条件较好。本研究选择在湄洲湾罗屿东南侧支水道设置测站,同步观测水深(潮汐)、潮流、悬沙,测站处水深9.77 m(以平均海平面计),观测时段为2007-08-14T19:00—08-15T20:00(大潮期),涵盖2个完整的半日潮周期,并对底质取样。研究海域及测站位置见图1。潮位采用水位计观测,海流、悬沙采用5层观测,潮流观测采用Aanderaa RCM9型海流计,悬沙使用采水器采集后,在实验室分析,并对涨落潮中间时刻与高低潮时刻4个特征时刻的悬沙粒度组成进行分析。

图1 研究海域及测站位置Fig.1 Study area and the location of observation site

1.2 一维水深平均悬沙模型

1)控制方程与假设

湄洲湾以M2,S2为主要潮流分量,本次观测时段内M2分潮流占比59%,S2分潮流占比18%,其他分潮流占比均小于9%,M4分潮流仅占比4%①国家海洋局第一海洋研究所.福建湄州湾电厂二期扩建工程可行性研究工程海域原型观测专题报告,2007.,因此本文模型水动力因素主要考虑M2,S2分潮,并进行适当简化。观测期间,测站处潮流流向几乎与水道走向平行,往复流态十分明显,涨潮流向40°,落潮流向217°,因此,本文使用一维水深平均悬沙控制方程来仿真所观测到的悬沙序列:

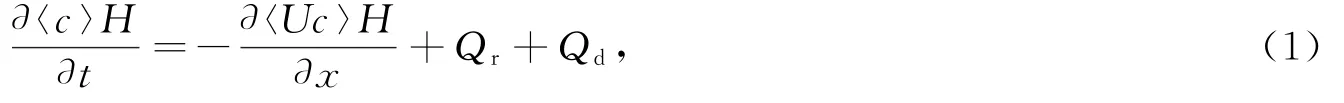
式中,c表示悬沙浓度；t表示时间；H表示水深；U表示海流流速,罗屿水道往复流特征显著,近似假设潮流为一维,以涨潮流方向为正；x为水平距离,正方向与海流方向一致；Qr与Qd则分别代表沉积物再悬浮量和沉降量。〈〉代表沿水深方向平均。由于研究测站处水动力条件较强,本次观测到的涨急流速达到68 cm/s,落急流速73 cm/s,水平扩散项量级远小于水平输沙项,忽略水平扩散项[9-10]。

式(1)中,平流项采用下列分解式表达:

式中,下标“d”代表该量与其垂向平均值的差。式(2)中等号右侧第二项代表垂向流速与悬沙浓度剖面特征之间的非线性相互作用,为了对模型进行简化,将该非线性项忽略[11-12]。最终,平流项可以表示为

式(1)中,再悬浮项由底层海流剪切海床产生,本文采用水深平均模型仿真悬沙变化,因此,为了表达再悬浮项Qr与垂向平均流的关系,采用如下方法计算[13]:

式(4)中,M表示泥沙单位起动量(单位面积、单位时间)；ρ表示海水密度；CD表示拖曳系数；τcr表示临界起动切应力。假设M,ρ,CD,τcr均为常数,因此影响沉积物再悬浮量的参数B简化为常数[14]。

悬沙沉降量与沉降速度成正比,并受海水底层悬沙和水深的影响,沉降项采用下式表达[3,14]:

式中,D=Kdws,ws表示泥沙沉降速度；cb表示海水底层悬沙质量浓度。最终,沉降项由垂向平均悬沙质量浓度、水深、沉降速度和沉降参数D表示。根据一维连续方程:

结合式(6)与式(3),并将式(1)～(6)合并,一维垂向平均悬沙模型控制方程表示为

式(7)表示,悬沙质量浓度的时间序列主要受3个物理过程控制,按等式右侧顺序依次是平流项、再悬浮项与沉积项。上述3项可使用简谐波表示[13]。式(7)中,垂向平均流速、总水深(水深与潮位之和)均可利用观测结果,通过调和分析表达,并可将式(7)以三角傅里叶变换的形式表示为

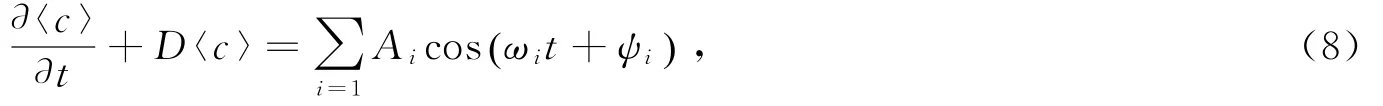
式中,Ai、ωi与ψi为各个傅里叶分量的振幅、角速度与初相位。将式(8)对时间积分后,悬浮泥沙浓度表示为

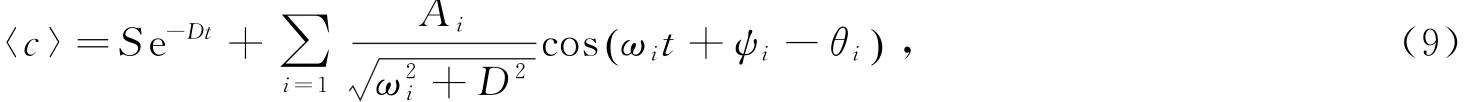
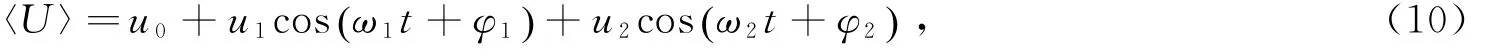
式中,u0表示余流；u1、ω1、φ1分别表示 M2分潮流的振幅、角速度与初相位；u2,ω2,φ2分别表示S2分潮流的振幅、角速度与初相位。相比于u0和u2,u1在量级上具有绝对优势,因此做如下变换:

相近地,水深可采用下式表示:

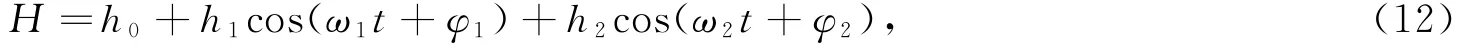
式中,h0为平均水深(以平均海平面计),h1,φ1分别为M2分潮的振幅和初相位；h2,φ2分别为S2分潮的振幅和初相位。由于测站平均水深是潮位振幅的4倍,因此做如下变换:

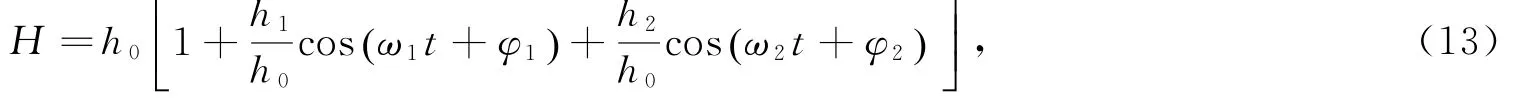
则式(7)再悬浮项中水深的倒数可表示为

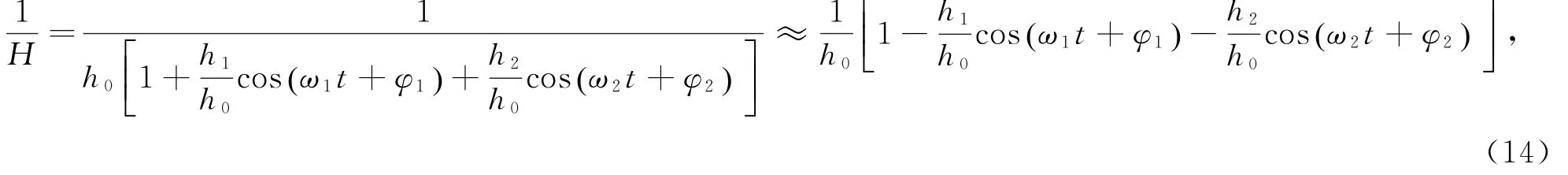
式(7)中平流项受悬沙浓度水平梯度控制,该量十分复杂,且难以观测,将该梯度进行简化,设水平浓度梯度为常数[3,9,15],悬沙质量浓度水平梯度表示为

结合式(7)、式(9)、式(11)和工(14),并将振幅中包含u0/u1,u2/u1,h1/h0与h2/h0的高阶项(阶数＞1)忽略[14],最终将悬沙分解为12个主要的傅里叶分量,其时间序列可表示为

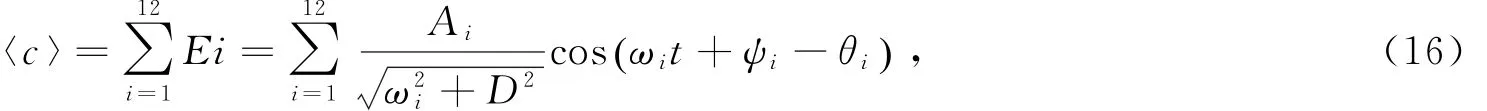
表1 三角傅里叶分量参数Table 1 Parameters of Fourier components

各傅里叶分量中(表1),E1代表在整个潮周期内悬沙的平均水平,不随时间变化,该分量由M2分潮流与余流共同作用下的水平输沙、M2分潮流剪切海底引起的再悬浮两部分组成,是这2个物理过程的叠加；E2也是2个物理过程的叠加,包括M2分潮流作用下的水平输沙、M2分潮流与余流共同作用剪切海底引起的再悬浮；E3,E4和E8三个分量同源,是M2分潮流剪切海底与M2分潮引起的水深变化共同作用产生的再悬浮项,通过三角变换分解为3个分量；E5是S2分潮流作用下的水平输沙项；E6,E11和E12三个分量同源,是M2分潮流剪切海底与S2分潮引起的水深变化共同作用产生的再悬浮项,通过三角变换分解为3个分量；E7分量是由M2分潮流剪切海底产生的再悬浮项,且不受其他动力因素控制；E9,E10两项同源,是M2分潮流与S2分潮流共同作用剪切海底产生的再悬浮项,通过三角变换分解为2个分量,且E10分量的角速度为M2与S2分潮角速度之差,具有半月潮周期,说明在M2与S2分潮的共同作用下,悬沙序列能够体现出半月潮周期变化。

2)参数设置

测站处底质粒径分布见图2a,低潮、涨急、高潮、落急四个特征时刻悬沙的粒径组成见图2b。测站处底质包含淤泥、粉砂与细砂各个成分,最大粒径2 mm,但悬沙成分仅包含淤泥、粉砂两种成分,最大粒径0.063 mm。观测结果说明细砂并未起动,因此模型将悬沙分为淤泥、粉砂两种组分进行模拟,以粒径0.016 mm代表粉砂,粒径0.002 mm代表淤泥组分,悬沙浓度为两者之和。

模型自由参数B,D,k与泥沙特性及海水特性等有关,如泥沙临界起动切应力、沉降速度等,由于其难以测定,在同类的模型研究中通常采用观测结果进行率定[9,16-17]。在率定前,部分参数可根据现有研究成果限定合理的取值范围。

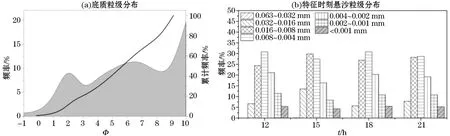
图2 底质与悬沙粒径组成Fig.2 Grain diameter compositions of sediment and suspension

k取值范围在-2.0×10-5～2.0×10-5kg/m4[14],本研究取k=-1.0×10-5kg/m4。单位起动量M取值范围在2.0×10-5～3.5×10-3kg·m-2·s-1[18],粉砂组分取3.5×10-3kg·m-2·s-1,淤泥组分取2.48×10-3kg·m-2·s-1。粉砂临界起动切应力τcr在0.05～0.13 N/m2[19],本文研究取0.05 N/m2；淤泥临界起动切应力τcr在0.05～0.2 N/m2[19-21],本研究取τcr=0.14 N/m2。CD取值5.0×10-3。海水密度ρ取1 025.0 kg/m3。粒径为0.01 mm的泥沙沉速大于0.07 mm/s[22],絮凝体的沉降速度小于3 mm/s[23]。对于各组分沉降速度ws,粉砂组分取1.06 mm/s[19]；淤泥组分沉降速度在0.003～0.2 mm/s[24],本文取0.2 mm/s。沉降参数Kd则较为复杂,影响因素包括垂向平均悬沙与近底层悬沙之比、水深等,经过率定,参数Kd粉砂组分取值1 800,淤泥组分取值4 680。由式(5)计算得到,粉砂组分D=0.195,淤泥组分D=0.096。

2 结果与验证

本期观测在大潮期内进行,观测到的最大潮差6.32 m,涨潮过程最大流速0.68 m/s,落潮过程最大流速0.73 m/s,悬沙质量浓度最高达到94.5 mg/L,最低质量浓度39.3 mg/L。对应时段内,经调和分析计算到的最大潮差6.01 m,涨潮过程最大流速0.73 m/s,落潮过程最大流速0.60 m/s,模拟得到的最高悬沙质量浓度81.9 mg/L,最低质量浓度42.0 mg/L。

将计算结果与观测资料比对验证,水深、潮流及悬沙质量浓度验证结果见图3a～3c,粉砂、淤泥组分占比验证见图3d,验证结果显示,计算结果与观测资料基本吻合,能够反映悬沙质量浓度随时间的变化趋势,粉砂、淤泥组分随时间变化的计算结果也与观测结果吻合。本文由于对模型进行简化,潮流仅考虑了M2,S2两个分量及余流,因此,潮汐、潮流计算结果与观测结果存在误差,且水动力计算误差可传递至悬沙计算,最终引发悬沙计算误差。除上述原因外,悬沙计算误差的产生原因还包括:1)虽然湄洲湾内波浪掩护条件较好,但依然受到波浪影响,因此悬沙的部分高频率的变化特征没有被仿真出来；2)测站处底质与悬沙的组成成分复杂,含有粉砂、淤泥的各个粒径成分,本文采用2种粒径的泥沙来代替成分复杂的混合物,因此存在计算误差。经准调和分析后,垂向平均流速及水深近似以式(10)及式(12)表示为

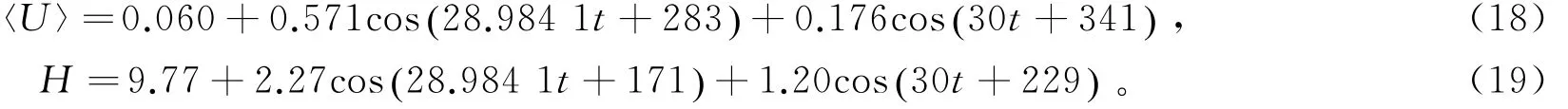
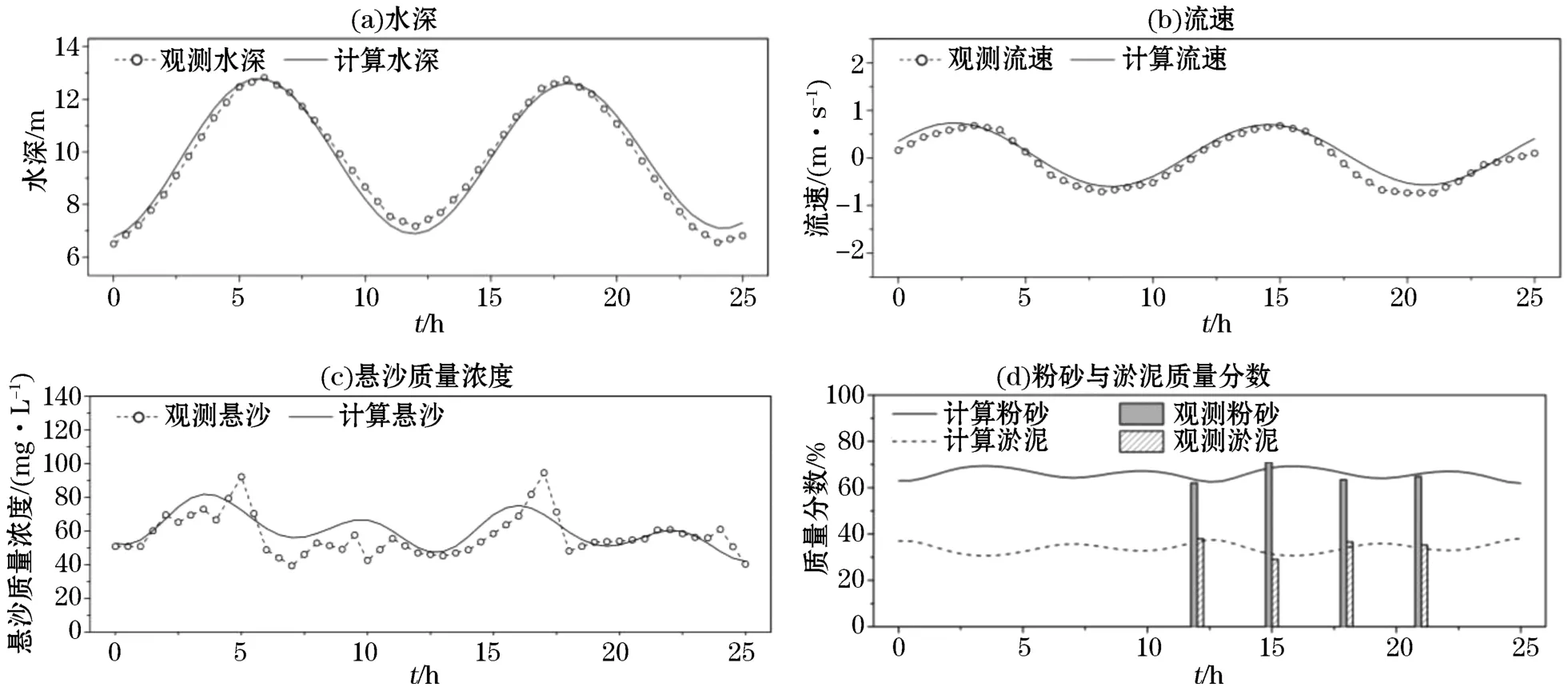
图3 计算结果验证Fig.3 Validadtion of model simulations

由于实际悬沙在海水中的运动是三维的,而本文采用一维水深平均模型进行简化,因此模型本身存在误差。观测期间,涨落潮流主流向相差177°,在平面上,本文模型简化为一维,这是造成模型从动力方面产生误差的一个方面。另一方面,本文选择垂向平均悬沙浓度作为研究指标,因此忽略了悬沙的垂向结构,没有能够反映海流作用下悬沙的垂向输运和垂向扩散两个物理过程,这会造成模型计算结果与实际观测结果之间存在浓度和相位两方面的误差。从模型验证结果来看,简化模型基本反映了实际情况,说明简化后的模型抓住了主要的物理过程。

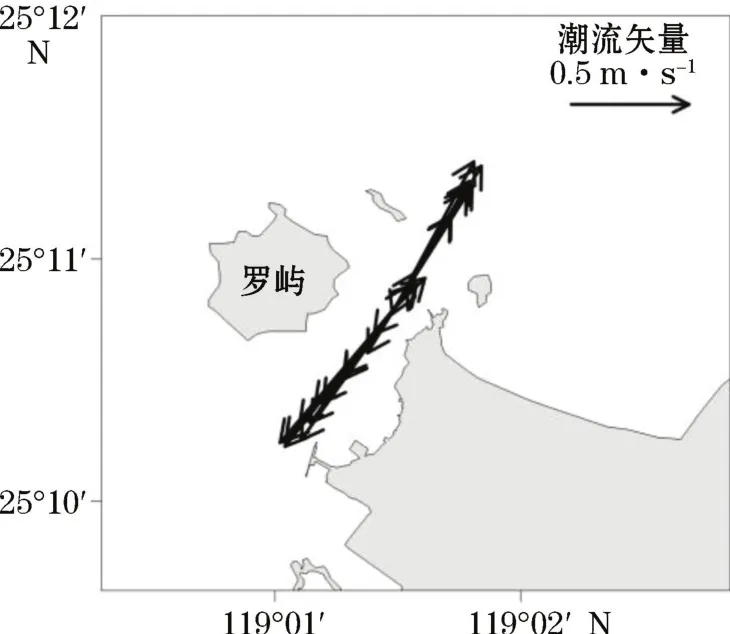
图4 潮流矢量图Fig.4 Tidal current vectors

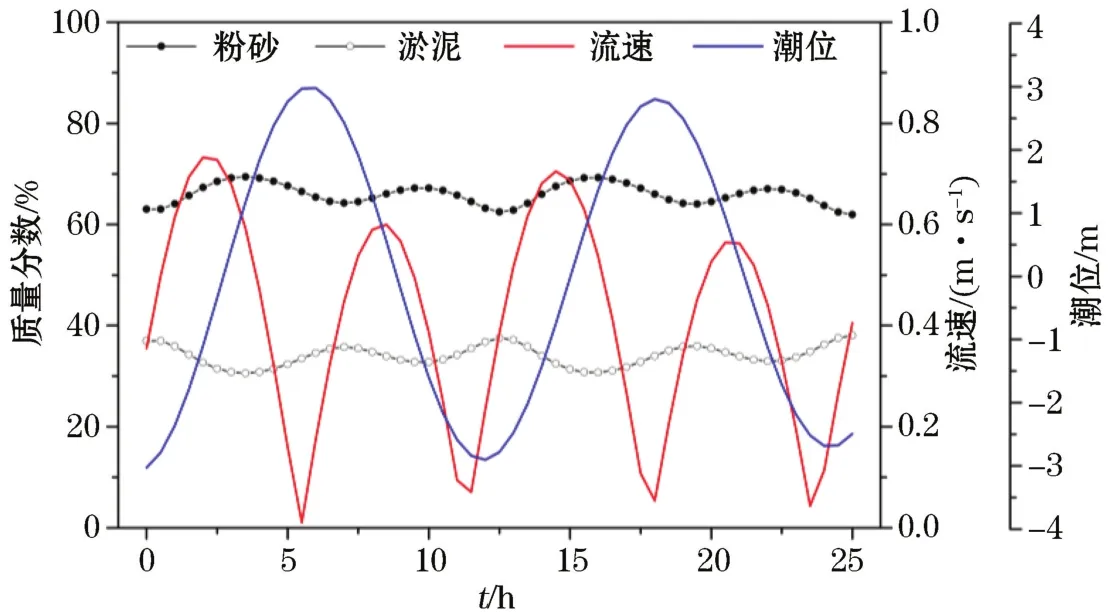
图5 悬沙组分质量分数对潮流的响应Fig.5 Responses of grain diameter composition to current

3 讨 论

3.1 各组分起动、沉降能力比较

图5所示为模型计算得到的粉砂、淤泥组分在悬沙中所占质量分数随潮流变化的过程,由于模型没有考虑波浪作用,剪切作用强弱仅与潮流流速有关,因此对流速取绝对值进行对照分析。在所模拟的2个半日潮周期内,粉砂所占质量分数在62.0%～69.4%,淤泥占比在30.6%～38.0%；在观测到的4个特征时刻,粉砂占比在62%～71%,淤泥占比在29%～38%。模拟与观测结果均显示,粉砂组分占优势。而底质分析结果显示,细砂占比21.6%,粉砂占比40.6%,淤泥占比37.8%,底质中粉砂与淤泥组分较为接近。从沉降角度考虑,粉砂组分由于粒径较粗,沉降速度高于淤泥。本文模型中沉降参数D经率定后,粉砂组分D=0.195,淤泥组分D=0.096,粉砂沉降能力明显高于淤泥。粉砂组分在沉降能力明显高于淤泥组分、且在底质中占比与淤泥组分接近的条件下,在悬沙中的占比明显高于淤泥,这说明,粉砂组分的起动能力明显高于淤泥组分,淤泥组分起动条件较高与黏性泥沙黏结力等特性有关[19]。由于粉砂组分的起动和沉降能力均高于淤泥组分,因此,悬沙中粉砂百分含量的极大值出现在动力条件较强时刻附近,约在涨落急时刻1.5 h后,淤泥质量分数的极大值则出现在动力较弱的涨落憩时刻1.5 h后,这说明,涨落急或涨落憩等潮流特征时刻所观测到的悬沙组成,并不能代表悬沙组成的极值,但采集到的悬沙样本基本包含了本地悬浮体中各粒径成分。

3.2 悬沙组分傅里叶分量

本文模型分解得到的12个傅里叶分量(表1)中,E1分量代表悬沙序列的平均水平,不随时间变化；E10分量的角速度为M2分潮与S2分潮角速度之差,具有半月潮周期,说明在M2与S2分潮共同作用下,悬沙能够表现出大小潮变化趋势,这是因为M2与S2分潮的角速度接近却不重合,但由于本文研究没有观测到完整的半月潮周期,因此主要讨论E2～E9,E11,E12分量。

图6所示为M2,S2分潮流及余流共同作用下,对粉砂、淤泥两种组分进行傅里叶分析得到的主要谐波分量,结果显示,2种悬沙组分均以E7为主要傅里叶分量,E7具有M2分潮2倍的角速度(表1),呈1/4日潮周期,是在M2分潮流的剪切作用下产生,揭示了半日潮海区在潮流作用下,悬沙呈1/4日潮周期的原因。其次,主要傅里叶分量还包括E2,E9,E3分量。E2由水平输沙、余流、M2分潮流共同作用产生,具有与M2分潮相同的角速度及半日潮周期；E9由M2,S2分潮共同作用产生,角速度为M2,S2分潮角速度之和,具有1/4日潮的周期；E3主要由M2分潮剪切海床产生,具有M2分潮的角速度及半日潮周期。总悬浮泥沙由各分量叠加而成,而上述4个主要傅里叶分量分别具有1/4日潮周期与半日潮周期,因而悬沙浓度在一个潮周期内呈现出不对称特征,即一个半日潮周期内两次峰值具有明显差异(图3c),这与观测结果吻合。

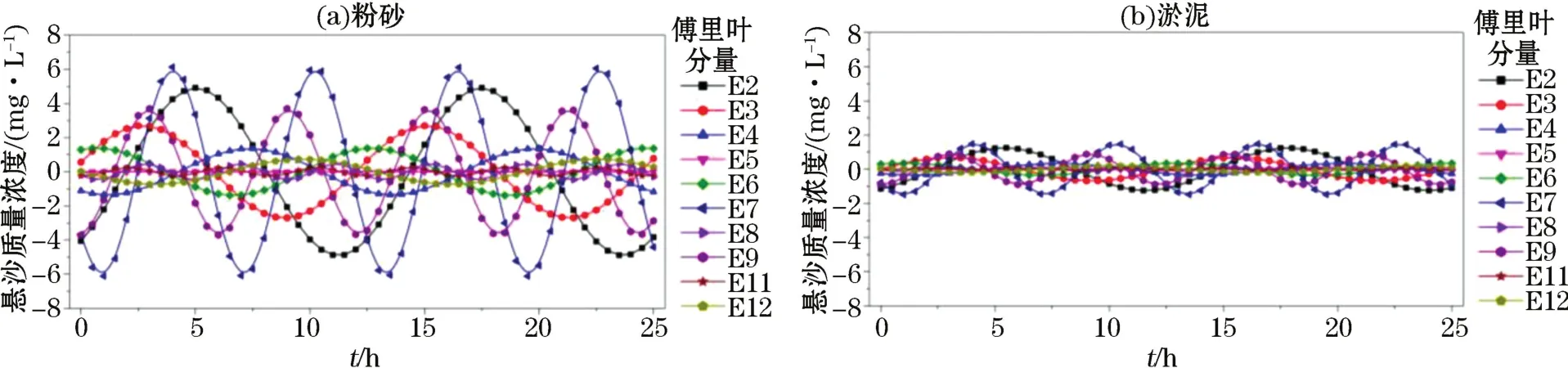
图6 傅里叶分量的时间序列Fig.6 Time series of Fourier components

对比图6a与图5b,粉砂组分各分量的振幅均显著高于淤泥组分,这是由于淤泥组分起动和沉降能力均弱于粉砂组分造成的。观测悬沙总质量浓度波动范围在39～95 mg/L,特征时刻观测到的粉砂组分波动范围在29～41 mg/L,淤泥组分波动范围在17～20 mg/L,观测结果也显示,粉砂组分的振幅明显高于淤泥组分。本次模型计算结果显示,总悬沙波动范围在42～82 mg/L,粉砂组分波动范围在26～57 mg/L,淤泥组分波动范围在16～25 mg/L,与观测结果基本吻合,趋势一致。作为主要傅里叶分量,粉砂组分的E7分量振幅为6.1 mg/L,而淤泥组分的E7分量振幅为1.5 mg/L；此外,粉砂组分的E2,E9,E3分量振幅分别为4.9,3.7和2.7 mg/L,淤泥组分的E2,E9,E3分量振幅分别为1.2,0.9和0.7 mg/L,均说明粉砂组分的波动幅度高于淤泥组分。

3.3 余流对悬沙组分的影响

为讨论余流对海区悬沙组分变化特征的影响,假定其他因素固定,对比真实余流(u0=0.06 m/s,最适率定值)、余流消失(u0=0)、余流增强一倍(u0=0.12 m/s)与余流反向(u0=-0.06 m/s)四种情况下悬沙组分百分含量的变化特征,如图7所示。对比结果显示,由于余流方向与涨潮流方向相同,当余流消失时,涨潮过程粉砂组分所占百分比将下降,落潮过程粉砂组分将升高,而淤泥组分则相反,且由于余流对主要半日潮傅里叶分量(E2)的影响,如果余流消失,半日潮周期内悬沙相邻的两个波峰之间的不对称性(涨潮过程波峰高于落潮过程波峰)减弱；当余流增强一倍时,半日潮周期内悬沙相邻波峰之间的不对称性将增强,涨潮过程粉砂组分占比将上升,淤泥组分将下降；当余流反向时,半日潮周期内悬沙相邻波峰之间的不对称性发生反转,变为涨潮过程波峰低于落潮过程波峰,涨潮过程粉砂组分将下降,淤泥组分将提高。

图7 余流对悬沙组分的影响Fig.7 Influence of residual current on suspended sediment components

4 结 论

以泥沙的起动、沉降和水平输运为主要物理过程,根据所研究海域动力环境,以M2,S2为主要潮汐、潮流分量,建立了一维水深平均悬沙模型,采用傅里叶分析方法,将悬沙时间序列分解为12个主要傅里叶分量,模拟了湄洲湾海域2个完整半日潮周期内悬沙中粉砂、淤泥两种组分的运动过程。模型能够与水动力、悬沙同步观测吻合,并能仿真出各粒级组分对潮流的响应规律。

模型分解得到的主要傅里叶分量具有M2分潮两倍的角速度与1/4日潮周期,该分量粉砂组分振幅6.1 mg/L,淤泥组分振幅1.5 mg/L；次主要傅里叶分量具有M2分潮的角速度,振幅受水平输沙、余流、M2分潮流共同影响,粉砂组分振幅4.9 mg/L,淤泥组分振幅1.2 mg/L；振幅第三的分量由M2,S2分潮共同作用产生,角速度为M2,S2分潮角速度之和,具有1/4日潮的周期,粉砂组分振幅3.7 mg/L,淤泥组分振幅0.9 mg/L。观测与模型主要分量均显示,粉砂组分振幅高于淤泥组分,这是由于粉砂组分单位起动能力强、沉降速度高造成的,且淤泥组分由于黏结力等因素,起动条件较高。

本文测站位置余流与涨潮流方向一致,余流的存在致使涨潮过程中粉砂组分含量所占百分比上升,而落潮过程下降,淤泥组分则相反。此外,傅里叶分析说明,具有半日潮周期的傅里叶分量中振幅最大者,其振幅受余流影响,因此余流影响了半日潮周期内悬沙波峰之间的不对称性,由于余流方向同涨潮流,涨潮时段悬沙波峰高于落潮时段内的波峰。