中国东部海域冬季风场与海浪场的关联特征分析

周媛媛周 林*关 皓杨 波

(1.解放军91208部队,山东 青岛266102；2.国防科技大学 气象海洋学院,江苏 南京211101；3.解放军61741部队,北京100085；4.解放军92682部队,广东 湛江524001)

冷空气大风是影响中国东部海域海浪场的主要灾害性天气[1-2]。研究表明[3],东亚大陆西北路、东路和西路的冷空气引起中国东部海域海上大风几率分别为61%,26%和13%。冬季是中国东部海域一年中风浪最大、破坏性最强的季节,已有研究表明[4-7],中国东部海域冬季海浪主要受东亚大陆强冷空气和大风的影响,东海和台湾海峡受其影响最大,大浪区一般出现在冷锋或气旋过境后数小时内。

以往研究大多从个例的角度探讨冬季冷空气对中国东部海域海浪的影响,较少从冬季平均状态关注风场与海浪场的关联。为进一步研究冬季中国东部海域海浪的发生、发展与低层风场的关系,本文将利用奇异值分解(Singular Value Decomposition,SVD)方法分析冬季提前0～5 d的东亚大陆地面风场与中国东部海域海浪的关系,以期发现前期地面风场与中国东部海域的海浪关系密切的作用时间、关键区以及演变规律,为中国东部海域的海浪预报寻找一些强信号因子。

1 研究方法和数据来源

1.1 研究方法

SVD法是一种寻找2组变量线性组合的方法,是分析2个要素场相关性的常用有效工具[4-5]。由于SVD方法是以两要素场之间的最大协方差为基础展开计算的,故每对SVD模态反映的是对应要素的扰动场变化。利用SVD方法既可以对2个标量气象要素场(如气温、降水量或位势高度)进行诊断分析[6-8],也可以对包含向量场(如风场)的两要素场进行奇异值分解[9-10],本文探讨风场与海浪场的关联,故采用王盘兴等[9-10]提出的向量SVD方法。

1.2 数据来源

风场数据截取于1993—2011年19 a冬季(前一年12月至次年2月共57个月)逐日的CCMP(Cross Calibrated Multi-Platform)全球风场[11-12]资料,其水平空间范围为100°～130°E,20°～60°N(图1a),水平分辨率取0.5°×0.5°。

海浪数据来自WAVEWATCHⅢ海浪模式模拟的与上述风场同一时间段的19 a冬季逐日中国东部海域有效波高资料。资料的水平空间范围为117°30'～129°00'E,22°～41°N(图1b),水平分辨率为0.5°×0.5°。该资料已和Jason系列卫星高度计资料进行过全面检验,本研究海区模拟波高与实测波高的相关系数大于0.7,平均相对误差小于18.5%。具体的数值模拟过程、参数设置以及模拟结果检验见周媛媛等[13],在此不再赘述。

图1 研究区域Fig.1 Study area

本文奇异值分解中,设风场变量场为右场,海浪变量场为左场。右场数据是由原始风场分解为u和v分量进行日平均后通过标准化处理所得,样本数目为9 882,时次为1 710。左场数据由模拟的有效波高日平均后通过标准化处理所得,去除陆点后样本数目为616,时次为1 710(为保证数据量的一致性,无论在闰年还是平年,每年2月均只取前28 d的数据,每天一组数据)。

为了研究风场与海浪场的滞后相关性,分别提取与海浪场同时次的风场、比海浪场提前1～5 d的风场共6组数据,分别对其与海浪场进行SVD分解,对比分析其关键区域和相关性最大日期。

2 结果分析

2.1 度量参数分析

将进行SVD的6组数据分别命名为SVD0～SVD5,其分别对应海浪场与提前0～5 d的风场数据。将SVD0～SVD5各组数据奇异值分解后前三模态对应的奇异值、协方差平方贡献率和时间序列相关系数列表比较(表1),可以看出,每组数据中的奇异值和协方差平方贡献率均呈随模态顺序增长而减小的趋势,且第一模态远大于其余2个模态,说明各组的第一模态在描述原始的2个标准化场中具有特别重要的意义。由于各组的协方差平方贡献率的第一模态和第二模态所占比重较大(二者之和均大于90%),因此,本文在做典型变量场总体相关分析时,重点关注前2个模态。从时间序列相关系数来看,每组数据的相关系数(均通过1%的显著性水平检验)随模态顺序增长呈现递减趋势,但变化幅度较小,说明在同一组数据中,虽然相关性随模态减小,但差别并不大,因此,在讨论异类相关系数时,重点关注各组的第一模态。

从各组数据的第一模态中可知,奇异值和相关系数均为SVD1＞SVD0＞SVD2＞SVD3＞SVD4＞SVD5,即提前1 d的第一模态的相关系数最大(0.75),SVD0第一模态(0.73)略小于SVD1第二模态(0.74)；协方差平方贡献率则是SVD0＞SVD1＞SVD2＞SVD3＞SVD4＞SVD5,其减小的幅度也较小,说明在6组数据中,SVD0和SVD1是相关性最强的2组数据,即:在本文中研究的区域内,海浪场与同时次的风场及提前1 d的风场相关性最大。但从海浪预报的角度看,提前1 d的地面风场分布和变化更具有实际意义。

2.2 典型变量场总体相关分析

由于SVD0和SVD1是相关性最强(在表1中奇异值、协方差平方贡献率和相关系数均为最大或次大)的2组数据,且SVD1第一和第二模态的相关系数(0.75和0.74)分别大于SVD0的第一、第二模态的相关系数(0.73和0.67),故本文重点分析提前1 d和同时次的风场与海浪场的奇异向量空间分布和时间系数曲线,探究它们的典型变量场总体相关状况。

提前1 d低层风场与海浪场的SVD奇异向量空间分布和时间系数曲线的第一、第二模态见图2和图3。由SVD1第一模态(图2)可见:风场(右奇异向量,图2a)在贝加尔湖以东大陆呈一反气旋辐散气流覆盖,风速大值区位于中国渤海、黄海和东海北部,东海南部尤其台湾岛以东风速相对较小,整个海区风向几乎为一致的西北风。海区浪场的特征向量(左奇异向量,图2b)均为正值,海浪大值区和大风区对应较好,大值区主要位于朝鲜半岛以南海域和台湾海峡,海岸附近波高等值线与海岸线平行,梯度较大。第一模态的模态相关系数为0.75,反映了第一模态左场(浪高)、右场(风场)有很好的总体相关性。与对应时间系数相结合,当时间系数为正值时,该模态主要表征了位于大陆的反气旋式扰动风场对中国东部海域海浪的影响,使东部海区海浪波高扰动相对增加。当时间系数为负值时,该模态主要表征了位于大陆的气旋式扰动风场对中国东部海域海浪的影响,由于海上扰动风场为偏南风,与冬季盛行偏北风反向,使东部海区海浪波高扰动相对减小。

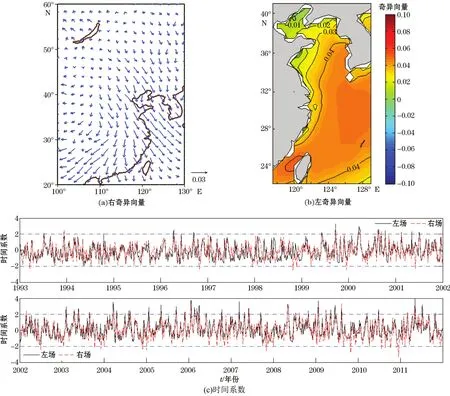
图2 SVD1第一模态的奇异向量空间分布和时间系数曲线Fig.2 Space distribution and time coefficient of the first mode of SVD1

由SVD1第二模态(图3)可见:影响海区的风场(图3a)是一个中心位于中国苏北平原(华北平原南端)东南部附近的反气旋扰动。受该反气旋辐散气流扰动影响,东海南部、台湾海峡、台湾岛以东洋面扰动风速较大,黄海和渤海风速较小,尤以反气旋扰动的涡旋中心附近的黄海中南部风速最小。与风场相对应的海浪场特征向量(图3b)的分布呈现以东海中部SW—NE走向零值线为界南北反相的变化；海浪场特征向量的大值区分布在南部的台湾海峡和南海北部以及北部的山东半岛周边海域。该分布型态和右场(风场)有较好的对应,第二模态的模态相关系数为0.74,亦即海浪场和风场时间系数随时间基本同步变化。结合第二模态的时间系数(图3c)可见,SVD1第二模态反映中国东部海域海浪场和风场的一种扰动模态,即中国东部海域的海浪受到苏北平原入海的反气旋(或气旋)扰动气流的影响。当时间系数大于零时,反气旋扰动风场增强,东海南部偏北扰动风速加大,风向与冬季盛行风(或背景风)风向一致,故波高扰动为正；而渤、黄海扰动风场风向与冬季盛行风向相反,故波高扰动为负。当时间系数为负值时,海域为气旋式扰动风场,东海南部偏南风扰动风速增大,风向与冬季盛行风(或背景风)风向相反,故波高扰动为负,而渤、黄海扰动风场风向与冬季盛行风向相同,故波高扰动为正。该模态主要反映了位于中国东部平原(华北平原和长江中下游平原附近)入海的大尺度气旋(或反气旋)扰动风场对中国东部海域海浪扰动的影响。

同时次的SVD0奇异向量空间分布和时间系数曲线的第一、第二模态见图4和图5。由图4、图5与图2、图3对比可以发现,SVD0和SVD1的第一模态与第二模态均十分相似。由SVD0第一模态(图4)可见,随着贝加尔湖以东反气旋扰动的南下,海区偏北大风扰动区也向南移动并覆盖整个中国东部海域,海区浪场的特征向量在朝鲜半岛西部和东海北部形成闭合高中心；而SVD0第二模态(图5)则反映出前一天中心位于中国苏北平原的反气旋扰动东移至朝鲜半岛南部,研究海区受其后半部影响,海区浪高仍存在南北反相的变化。第一模态(图4c)的模态相关系数为0.73,它和SVD1第一模态(图2c)相关系数也十分相似。从第一模态时间系数的逐年变化来看,1999年前冬季逐日振幅相对较小,海浪场6个时次、风场4个时次超过2.0,1999年后时间系数的振幅明显变大,海浪场71个时次、风场38个时次超过2.0,特别是在2004年、2006年、2008年、2009年和2011年冬季,有些天时间系数有长长的拖尾现象,振幅接近4.0,这反映1999年后该区域风场风速和浪场波高扰动变化比1999年前剧烈。第二模态(图5c)的模态相关系数为0.67,也和SVD1第二模态(图3c)相关系数相似；比较第二模态的时间系数的逐年变化,可以发现时间系数有较明显的负拖尾现象,即海浪场66个时次、风场54个时次时间系数小于-2.0,对比时间系数大于2.0的海浪场和风场分别有20和27个时次,意味着该海域冬季常发生由东部平原入海的气旋式扰动,造成黄海和渤海扰动波高增加,东海南部海域波高减小的扰动现象。

图5 SVD0第二模态的奇异向量空间分布和时间系数曲线Fig.5 Space distribution and time coefficient of the second mode of SVD0

2.3 风场影响海浪场的关键区分析

SVD的异类相关系数分布型代表了两变量场相互关系的分布结构,分析异类相关系数场可以寻找一个场对另一个场相互影响的关键区。图6a～图6l分别为当天至提前5 d的异类相关系数场的第一模态。

由图6可知,当天(图6a和图6g)影响海区浪场的扰动风场关键区(大值偏北风)主要位于海区的海面,海浪场的大部分海域的相关系数均超过0.5,最大值大于0.7,位于黄海南部和东海北部；提前1 d时(图6b和图6h)扰动风场关键区向中国渤海北部北上,海浪场的相关系数场和同时次的相似,大值区整体略有南移,大于0.7的高值区范围有所扩大,除东海北部外,台湾海峡也出现大于0.7的高值区；提前2 d时(图6c和图6i)扰动风场关键区已移至内蒙古、蒙古和中国东北平原西部,海浪场的相关系数场分布形态和前一天相似,但相关系数减小,大于0.6的高值区位于东海和台湾海峡；提前3 d时(图6d和图6j)扰动风场关键区已移到贝加尔湖以东以及蒙古国附近,海浪场的相关系数场大值区继续南移并减小,大于0.5的高值闭合区位于台湾海峡和台湾岛东北部海域；提前4 d和5 d时,扰动风场(图6k和图6l)关键区已移到贝加尔湖以北和西北附近,而海浪场(图6e和图6f)的相关系数场闭合大值区已消失,海域最大相关系数分别不超过0.4和0.3,且提前4 d和5 d的第一模态相关系数仅为0.38和0.29(表1),所以对于影响中国冬季中国东部海域海浪的大风的关键区可以提前3 d出现在贝加尔湖东南以及蒙古国附近,并随着时间的临近通过偏北风逐步由蒙古、内蒙古南下影响我国东北和华北,最后到达中国东部海域,影响关系最密切的海区为东海和台湾海峡。

3 结 论

通过对数值模拟的1993—2011年中国东部海域19 a冬季逐日海浪场与提前0～5 d的东亚大陆地面风场进行SVD分析,探究冬季逐日风场与海浪场的关联,找寻地面风场对海浪场的作用时间、关键区以及演变规律,得到结论:

1)SVD分析揭示了冬季提前0～5 d的逐日地面风场变化与海浪场变化有显著的联系,尤其是提前1 d的风场与海浪场的关联更有意义。

2)SVD第一模态反映了来自贝加尔湖以东反气旋(或气旋)式扰动南下的偏北(偏南)扰动大风对海面浪场波高扰动的影响；第二模态代表中国东部平原入海的气旋式(占多数)或反气旋式(占少数)扰动风场对中国东部海域海浪波高扰动的影响。1999年后研究区域的风速和浪高扰动变化比1999年前剧烈。

3)SVD分析揭示出冬季影响中国东部海域海浪的扰动大风关键区可以提前3 d出现在贝加尔湖以东以及蒙古国附近,并随着时间的临近通过偏北风逐步由蒙古、内蒙古南下影响中国东北和华北,最后到达中国东部海域,影响关系最密切的海区为东海和台湾海峡。