基于线性规划的煤炭运输问题研究

施 文

(上海市第二中学 上海 200031)

一、线性规划基本原理简述

求解最优化问题一般用线性规划的方法。[1-3]最优化问题是指：在一组约束条件的限制下，求目标函数的最大值或者最小值。当目标函数和给定的约束条件是全部是线性函数时，这个最优化问题即可转化为线性规划问题；当目标函数和给定的约束条件中只要有一个不是线性的，则不能看作线性规划问题。目标函数以及约束条件通常是在实际问题中根据人为理解为解决问题而建立的。[4-7]线性规划一般的求解步骤在高中阶段学校已经学习，一般步骤是这样的：列出目标函数以及约束条件；在二维直角坐标系画出约束条件表示的可行域；在可行域内找到目标函数的最优解。[8]由于很多实际问题的约束条件较为复杂，并不能直观地在二维直角坐标系中直接画出可行域，本文采用了计算机处理的方式，解决了这一难点。

二、研究问题

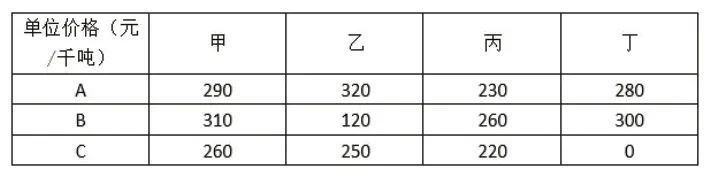
现有甲乙丙丁四个钢铁厂，钢铁厂所需的煤炭由A、B、C三个煤场供应。四个钢铁厂每天必须得到保证的供应量为30、70、10、10千吨。但由于煤炭资源紧缺，三个煤场煤炭最多只能分别供应50、60、50千吨煤炭。三个煤场的煤通过统一的煤炭运输管理站被运往四个钢铁厂。由于地理位置的差别，现在各煤场向煤炭输送管理站所需支付的费用不同。根据规定，现C煤场发往丁钢铁厂的煤由于政策原因，暂时不用支付管理费用，其他管理费用都是450元每千吨。根据规定，各个钢铁厂按照统一标准900元每千吨收费。此外，四个钢铁厂都向煤炭运输管理站申请了额外用量，分别为每天50、70、20、40千吨。那么请问煤炭输送站应该如何分配供煤量，才能获利最多。各煤炭场运输煤炭到各钢铁厂的单位价格见表1，各个钢铁厂需求量及额外用量见表2，各个煤炭场输出量见表3。

表1 各煤炭场运输煤炭到各钢铁厂的单位价格

表2 各个钢铁厂需求量及额外用量

表3 各个煤炭场输出量

三、问题分析

煤炭运输管理站分配三个煤场向四个钢铁厂运煤的方案是为了获利最多。而从给出的数据看，A、B、C三个煤炭厂的总供煤量为160千吨，不会超过四个钢铁厂的基本煤炭用量与额外煤炭用量总和300千吨，因而可以全部输出并获利。于是煤炭输送管理中心的收入是900*(50+60+50)=144000(元)。同样，其他费用也是固定的，为450*(50+60+50)=72000(元)。要使利润最大，则需使管理费最少。

四、建立模型

1.确定决策变量：

记x11为A输送至甲的煤炭量，x21为A输送至乙的煤炭量，x31为A输送至丙的煤炭量，x41为A输送至丁的煤炭量；x12记为B输送至甲的煤炭量，x22为B输送至乙的煤炭量，x32为B输送至丙的煤炭量，x42为B输送至丁的煤炭量；记x13为C输送至甲的煤炭量，x23为C输送至乙的煤炭量，x33为C输送至丙的煤炭量，x43为C输送至丁的煤炭量。

2.确定约束条件：

决策变量均有范围限制，因为所有钢铁厂必须正常工作，所有煤炭输出量不能低于需求量，且受限于上限。而且钢铁厂必须用完煤炭场产能。煤炭场的供煤量可表示为以下三个式子。

各个钢铁厂需求量可表示为以下四个式子。

3.确定目标函数为：

综合如上分析得到规划模型为：

这是一个线性规划模型，可以利用Python代码求解，代码如下所示。

结果方案为：A煤炭场向乙钢铁厂供50千吨。B煤炭场向乙钢铁厂供20千吨，向丁钢铁厂供40千吨。C煤炭场向甲钢铁厂供40千吨，向丙钢铁厂供10千吨。煤炭输送管理费为24400元。最后计算得出利润是，总收入减去其他管理费用再减去输送管理费用，共47600元。

五、模型扩展

如果A、B、C三个煤场的每天最大供煤量扩大一倍，则总供煤量为320千吨，大于需求量300千吨。那么这种情况下煤炭不能全部被卖出。那么煤炭输送管理站应该如何设计分配方案，达到利益最大化呢？先计算供应每千吨的净利润，从收入中减去管理费。得到新的纯利润表。

?

决策变量仍为xij表示煤场j每天向i钢铁厂的供煤量。由于C与丁之间没有运输渠道，所以x43=0。约束条件：由于煤不能全部卖出，应将小于号改为小于等于号，需求量限制不变。约束条件的式子如下所示：

目标函数如下：

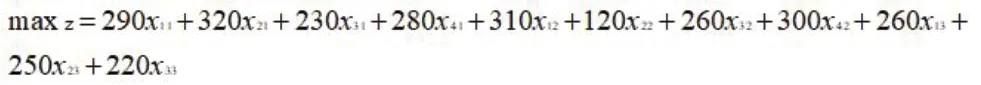
所以模型可以表示如下形式：

利用python代码求解：

得到方案为：A向乙钢铁厂供煤100千吨，B向甲、乙、丁钢铁厂分别供30、40、50千吨，C向甲、丙钢铁厂分别供50、30千吨，总利润为88700元。

六、总结

模型考虑的是，将某种物资从若干物资运往需求点，在供应量约束条件下，使总费用最小或总利润最大。这一类问题一般称为运输问题，是线性规划应用最广泛的领域之一。[9]在标准的运输问题中，供需量一般是平衡的，即供应点的总供应量等于需求点的总需求量。[10]模型扩展中供需量不平衡，但这并不会引起本质区别，一样可以用线性规划模型求解。